数据结构:堆的实现与建堆时间复杂度分析

news2024/9/27 7:18:01

目录

前言

一.堆的介绍

1.堆的本质

2.堆的分类

二.堆的实现(以小根堆为例)

1.关于二叉树的两组重要结论：

2.堆的物理存储结构框架(动态数组的简单构建)

3. 堆元素插入接口(以小根堆为例)

堆尾元素向上调整的算法接口:

4.堆元素插入接口测试

5.堆元素插入接口建堆的时间复杂度分析(建堆时间复杂度)

6.堆元素删除接口(同样以小根堆为例子)

堆元素向下调整算法接口实现:

7.堆元素删除接口测试

8.逐个删除堆顶数据过程的时间复杂度分析(删堆的时间复杂度分析)

9.堆的实现代码总览(以小根堆为例)

10.结语

 

 

前言

关于数据结构的文章:写博客的时候我感觉在表达层面上有点费劲,如果文章整体在表述上让人感觉不够清楚,恳请读者原谅,本菜狗已经尽力了.

一.堆的介绍

1.堆的本质

关于二叉树的图论基础参见:http://t.csdn.cn/Nv325http://t.csdn.cn/Nv325青菜友情提示:基础概念对于理解堆的实现与运用非常重要

堆的本质是映射在内存中顺序存储结构(数组)上的完全二叉树(完全二叉树是堆的逻辑结构).

堆的图解:

  • 结点中的数据存储在相应下标的数组元素空间中

2.堆的分类

堆的两个类型：

  1. 大根堆:在大根堆中任何子结构的父结点中存储的值大于其左右孩子结点中存储的值
  2. 小根堆:在小根堆中任何子结构的父结点中存储的值小于其左右孩子结点中存储的值

二.堆的实现(以小根堆为例)

1.关于二叉树的两组重要结论：

  • 堆的任何一个父结点的编号parent与其左孩子结点的编号leftchild满足如下关系式:
  • 堆的任何一个父结点的编号parent与其右孩子结点的编号rightchild满足如下关系式:

这两组重要结论的推导和分析参见青菜的博客:http://t.csdn.cn/Nv325http://t.csdn.cn/Nv325

2.堆的物理存储结构框架(动态数组的简单构建)

堆是存储在数组上的(大小根)完全二叉树,因此在实现堆之前我们先构建一个简单的动态数组作为物理存储结构框架:

  • 维护动态数组的结构体: 
    typedef int HPDataType;   //堆元素类型
typedef struct Heap
{
	HPDataType* arry;     //堆区内存指针
	size_t size;          //堆元素个数
	size_t capacity;      //数组的空间容量
}HP;
  • 堆的基础操作接口声明： 
    //维护堆的结构体的初始化接口
void HeapInit(HP* php);


//销毁堆的接口
void HeapDestroy(HP* php);


//堆元素的打印接口
void HeapPrint(HP* php);


//判断堆是否为空(堆中有无元素)的接口
bool HeapEmpty(HP* php);


//返回堆中元素个数的接口
size_t HeapSize(HP* php);


//返回堆顶元素(即编号为0的元素)的接口
HPDataType HeapTop(HP* php);
  • 基础接口的实现: 
    //堆结构体的初始化接口
void HeapInit(HP* ptrheap)
{
	assert(ptrheap);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;

}


//销毁堆的接口
void HeapDestroy(HP* ptrheap)
{
	assert(ptrheap);
	free(ptrheap->arry);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;
}


//堆的打印接口
void HeapPrint(HP* ptrheap)
{
	assert(ptrheap);
	size_t tem = 0;
	for (tem = 0; tem < ptrheap->size; ++tem)
	{
		printf("%d->", ptrheap->arry[tem]);

	}
	printf("END\n");
}



//判断堆是否为空的接口
bool HeapEmpty(HP* ptrheap)
{
	assert(ptrheap);
	return (0 == ptrheap->size);
}


//返回堆元素个数的接口
size_t HeapSize(HP* ptrheap)
{
	assert(ptrheap);
	return ptrheap->size;
}


//返回堆顶元素的接口
HPDataType HeapTop(HP* ptrheap)
{
	assert(!HeapEmpty(ptrheap));
	return ptrheap->arry[0];
}

    主函数建堆时的内存布局简单图示:

    堆区上的数组是在堆元素插入接口中调用malloc申请出来的(我们暂时还没有实现堆元素插入的接口)

  • 以上是堆在内存中的存储框架的构建,然而堆的核心接口是堆元素的插入和删除接口

3. 堆元素插入接口(以小根堆为例)

  • 堆的构建过程概述:向堆尾逐个插入元素(将元素尾插进数组中),每次插入一个元素后都通过堆的调整算法逐层向上(二叉树意义上的层)(子结点和父结点进行大小比较,若不满足小根堆的性质就进行数值交换)调整该元素在堆中的位置以保持小根堆的数据结构.
  • 算法过程简图:
  • 从0个结点的堆开始,每尾插一个元素我们都按照小根堆的性质(通过元素向上调整算法)调整该元素在堆中的位置来保持小根堆的数据结构,我们就是以这样的基本思想来建堆的.
  • 建堆的思路细解:

  • 显然在堆尾插入元素6后破坏了小根堆的结构(6小于其父结点20不满足小根堆的性质)(将任意一个子结构中子结点与父结点进行大小比较就可以知道堆的结构有没有被破坏),因此我们就需要将6这个元素逐层向二叉树的上层调整(每个调整的子步骤都是从子结点向父结点调整)
  • 通过树的子结构中子结点与父结点的编号关系可以找到堆尾8号结点(元素6)的父结点(元素20,结点编号为3)
  • 接下来将元素逐层向上调整(子结点和父结点进行数值交换)来恢复小根堆的数据结构:

向上调整的第一步:将尾插进堆尾的结点(8号结点,值为6)与其父结点(3号结点,值为20)进行比较,父结点大于子结点,交换父结点与子结点的值(下图中的Swap是元素数值交换接口):

向上调整的第二步:交换了8号结点和3号结点的值后,我们发现小堆结构依然不成立,于是重复上述的调整过程,将元素6继续向上层的父结点位置进行调整,不断重复迭代直到小堆结构恢复或者元素6被调到堆顶为止:

  • 可见经过再一次调整后,元素6来到了1号结点,此时1号结点大于0号结点,小堆数据结构得到恢复,调整过程终止。

同时不难分析出,任何堆尾元素向上调整的过程都是在堆尾到堆顶元素的连通路径上进行的(该路径长度数量级为logk)(k为当前树结点总个数)):

  • 根据上面的分析我们可以设计出一个堆尾元素向上调整的算法接口:

接口首部: arry是指向数组首地址的指针,child是堆尾元素的编号(结点编号同时也是该元素的数组下标)

void AdjustUp(HPDataType* arry, size_t child);

堆尾元素向上调整的算法接口:

//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}



//小堆元素的向上调整接口
void AdjustUp(HPDataType* arry, size_t child)  //child表示孩子结点的编号
{
	assert(arry);
	size_t parent = (child - 1) / 2;    //算出父结点的数组下标(堆编号)
	while (child > 0)			        //child减小到0时则调整结束(堆尾元素已调到堆顶)
	{
		if (arry[child] < arry[parent]) //父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + child, arry+parent);
			child = parent;				//将原父结点作为新的子结点继续迭代过程
			parent = (child - 1) / 2;	//算出父结点的数组下标(堆编号)
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构恢复,无需再调整
		}
	}
}

堆尾元素向上调整的算法接口中需要注意的细节:

  • 调整循环的终止条件有两个:
  1. 一个是被调整元素被调到了堆顶(即child=0的时候)
  2. 当被调整元素大于其父结点时小堆的数据结构得到恢复,break终止循环

有了该接口,我们就可以设计堆元素插入接口:

  • HP * ptrheap是指向堆结构体的结构体指针,x是要插入的元素的数值
void HeapPush(HP* ptrheap, HPDataType x)
// 插入一个小堆元素的接口
// 插入x以后，保持其数据结构依旧是小堆
void HeapPush(HP* ptrheap, HPDataType x)        //ptrheap是指向堆结构体的结构体指针
{
	assert(ptrheap);
	if (ptrheap->capacity == ptrheap->size)	    //数组容量检查,容量不够则扩容
	{
		size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;
        //注意容量为0则将堆区数组容量调整为4
		HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity*sizeof(HPDataType)); //空间不够则扩容
		assert(tem);             //检查扩容是否成功
		ptrheap->arry = tem;     //将堆区地址赋给结构体中的指针成员
		ptrheap->capacity = newcapacity; //容量标记更新
	}
	ptrheap->arry[ptrheap->size] = x;			//元素尾插入堆
	ptrheap->size++;


	//将尾插的元素进行向上调整以保持堆的数据结构(复用元素向上调整接口)
	AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知堆尾元素                
                                                //在二叉树中编号为size-1
}
  • 该接口可以完成一个堆元素的插入(而且每次完成插入后小根堆的数据结构都可以得到保持)
  • 如果我们想要创建一个n个元素小根堆,则n次调用HeapPush接口即可

4.堆元素插入接口测试

现在我们试着用HeapPush接口来构建六个元素的小堆,并将堆打印出来观察其逻辑结构:

  • 主函数代码: 
    int main ()
{
    HP hp;              //创建一个堆结构体
	HeapInit(&hp);      //结构体初始化
	HeapPush(&hp, 1);   //调用堆元素插入接口建堆
	HeapPush(&hp, 5);
	HeapPush(&hp, 0);
	HeapPush(&hp, 8);
	HeapPush(&hp, 3);
	HeapPush(&hp, 9);
	HeapPrint(&hp);     //打印堆元素
}

    我们来观察一下打印出来的小根堆的逻辑结构:

5.堆元素插入接口建堆的时间复杂度分析(建堆时间复杂度)

  • 假设现在我们要调用HeapPush接口来创建一个N个元素的小堆(调用N次HeapPush接口)
  • 注意:我们只关注时间复杂度最坏的情况(即假设每个插入堆尾的元素都沿着连通路径向上调整到了堆顶)
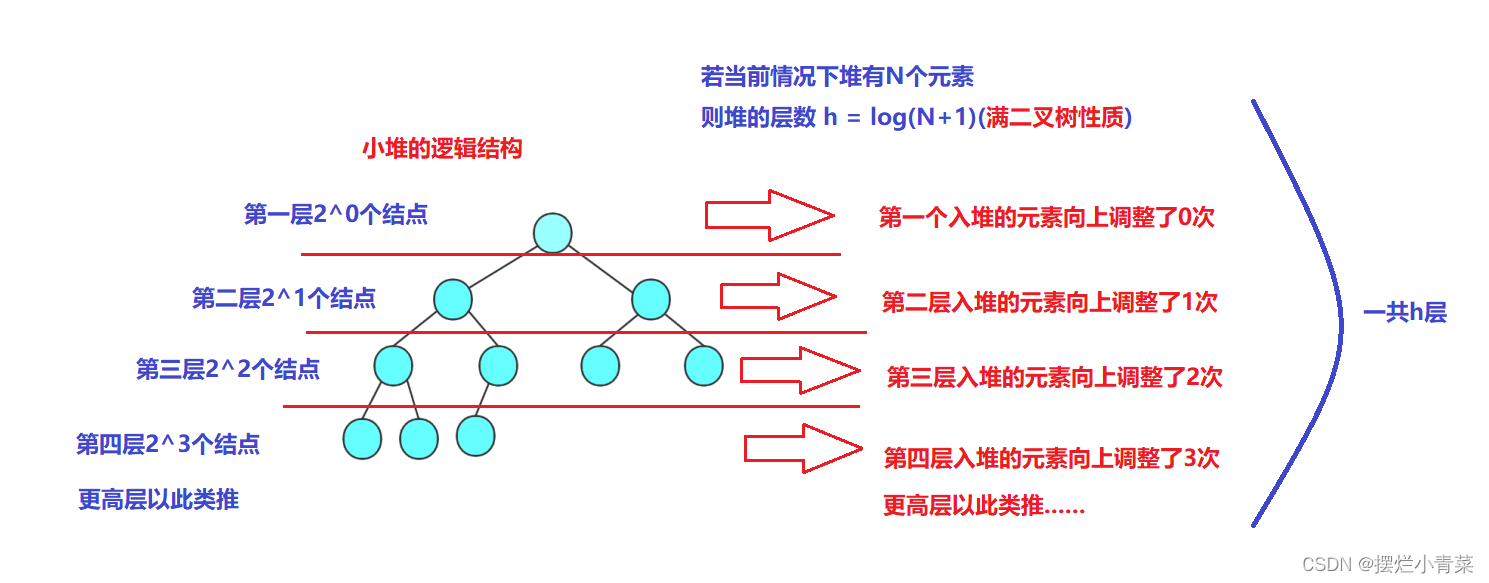
  • 分析建堆的时间复杂度时我们将堆看成满二叉树(满二叉树是特殊的完全二叉树),也就是说当堆有N个元素时,堆的层数h=log(N+1)(该对数以2为底,计算机科学中我们一般不关注对数的底数)
  • 接下来我们将所有元素的向上调整次数进行求和,即可得出用HeapPush接口建堆的时间复杂度:
  • 用错位相减法可对上面公式进行求和计算:
  • 因此可以得到用堆元素插入接口(堆元素向上调整算法)建堆(建立N个元素的小根堆)的时间复杂度为:O(N)=NlogN;

6.堆元素删除接口(同样以小根堆为例子)

我们讨论的堆元素删除指的是:删除堆顶数据

删除堆顶的元素的基本思路:

  • 先将堆顶元素与堆尾元素进行交换,然后令维护堆的结构体中的size(记录堆元素个数的成员变量)减一(相当于移除堆尾元素)
  • 然而原来的堆尾元素被交换到堆顶位置后,小根堆的数据结构会被破坏,因此我们需要将堆顶元素进行向下调整操作:
  • 堆顶元素向下调整图解演示:
  • 通过算法图解分析我们可以设计一个堆元素向下调整算法接口: 

arry是指向内存堆区数组首地址的指针,size是堆的结点总个数,parent是待调整结点在堆中的编号;

void AdjustDown(HPDataType* arry,size_t size,size_t parent)

堆元素向下调整算法接口实现:

//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}

//小堆元素的向下调整接口
void AdjustDown(HPDataType* arry,size_t size,size_t parent)
{
	assert(arry);
	size_t child = 2 * parent + 1;   //确定父结点的左孩子的编号
	while (child < size)			 //child增加到大于或等于size时说明被调整元素被调整到了叶结点上,调整过程结束
	{
		if (child + 1 < size && arry[child + 1] < arry[child])//确定左右孩子中较小的孩子结点
		{
			++child;   //条件成立说明右孩子较小,child更新为右孩子编号
		}
		if ( arry[child] < arry[parent])//父结点大于子结点,则父结点需要下调以保持小堆的结构
		{
			Swap(arry + parent, arry + child);//父子结点进行值交换
			parent = child;				      //将原来的子结点作为新的父结点继续迭代过程
			child = 2 * parent + 1;		      //继续向下找另外一个子结点
		}
		else
		{
			break;						//父结点不大于子结点,则小堆结构成立,无需继续调整
		}
	}
}
  •  注意一下算法接口的一些细节和边界条件:
  1. child<size说明被调整元素已经被调整到叶结点位置,结束调整过程
  2. 算法接口中我们只设计了一个child变量来记录当前父结点的孩子结点的编号,接着通过arry[child + 1] < arry[child]来比较左右孩子大小来确定child到底是取左孩子的编号还是取右孩子的编号(注意child+1<size判断语句是为了确定右孩子是否存在)
  • 有了堆元素向下调整算法接口我们就可以实现堆顶数据删除接口: 
    //删除堆顶元素
void HeapPop(HP* ptrheap)
{
	assert(ptrheap);
	Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素
	ptrheap->size--;										//删除堆尾元素
	AdjustDown(ptrheap->arry, ptrheap->size, 0);    //将堆顶元素进行向下调整以保持堆的数据结构
}

    注意:AdjustDown接口的传参中,ptrheadp->size指的是堆元素的总个数,由于我们要将堆顶元素向下调整,因此传入的被调整结点编号为0

  • 该接口每调用一次就可以删除一个堆顶数据(并保持小根堆的数据结构):

7.堆元素删除接口测试

我们先6次调用HeapPush接口创建一个六个元素的小堆,然后再6次调用HeapPop接口逐个删除堆顶元素(每删除一个堆顶数据打印一次堆,借此观察每次删除堆顶数据后堆的数据结构).

int main ()
{
    HP hp;
	HeapInit(&hp);
	HeapPush(&hp, 1);
	HeapPush(&hp, 5);
	HeapPush(&hp, 0);
	HeapPush(&hp, 8);
	HeapPush(&hp, 3);
	HeapPush(&hp, 9);
	HeapPrint(&hp);

	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);
	HeapPop(&hp);
	HeapPrint(&hp);


	HeapDestroy(&hp);

}

观察小根堆的数据结构(逻辑结构): 

  • 可见逐个删除堆顶数据的过程中小根堆的数据结构得到了保持

8.逐个删除堆顶数据过程的时间复杂度分析(删堆的时间复杂度分析)

假设现在有一个N个元素的小根堆,我们逐个删除堆顶数据直到将堆删空。

现在我们来分析这个过程的时间复杂度(我们同样将二叉树看成满二叉树来分析):

  • 同样我们考虑的是时间复杂度最坏的情况:即每次调用堆元素删除接口后,被交换到堆顶的元素都沿着连通路径向下被调整到叶结点
  • 分析：假设堆的高度为h,则满树的总结点个数N为  : 2^h - 1 
    需要注意的是满树的第h层(最后一层)的结点个数为: 2^(h-1)

所以满树的最后一层的结点个数占树的总结点个数的一半

因此如果我们删去满树的前h-1层的所有结点,则由最后一层结点所构成的新树的高度大致为h-1:

这也就意味着,在删除前h-1层结点的过程中树的总高度几乎不会发生变化:

因此可以得到删除满树的前h-1层所有结点过程中,每个被交换到堆顶的元素都要被向下调整log(N+1)次,则删除满树的前h-1层所有结点过程中,向下调整算法中循环语句执行总次数约为:

接着,对于由原树的最后一层(第h层)结点构成的新树(层数为h-1层)我们可以作类似的分析(即先删除其前h-2层结点,得到由其第h-1层结点构成的新树),以这种方式递推下去直到树被删空为止:

  • 由此可得, 逐个删除堆顶数据直到将堆删空过程中,堆元素的向下调整算法中循环语句总的执行次数估算为:

该多项式的和化为大O阶渐进表示法结果为O(NlogN). 

  • 逐个删除堆顶数据直到将堆删空的过程的时间复杂度分析为:O(NlogN)

9.堆的实现代码总览(以小根堆为例)

接口和结构类型声明的头文件:

#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <stdbool.h>
#include <time.h>

//实现小堆

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* arry;
	size_t size;
	size_t capacity;
}HP;


//堆的初始化接口
void HeapInit(HP* php);
//销毁堆的接口
void HeapDestroy(HP* php);
//堆的打印接口
void HeapPrint(HP* php);
//判断堆是否为空的接口
bool HeapEmpty(HP* php);
//返回堆元素个数的接口
size_t HeapSize(HP* php);
//返回堆顶元素的接口
HPDataType HeapTop(HP* php);


void Swap(HPDataType* pa, HPDataType* pb);
//堆元素向上调整算法接口
void AdjustUp(HPDataType* a, size_t child);
//堆元素向下调整算法接口
void AdjustDown(HPDataType* a, size_t size,size_t parent);
// 插入元素x以后，保持数据结构是(大/小)堆
void HeapPush(HP* php, HPDataType x);
// 删除堆顶的数据后,保持数据结构是(大/小)堆
void HeapPop(HP* php);

各个堆操作接口的实现:

#include "heap.h"


//堆的初始化接口
void HeapInit(HP* ptrheap)
{
	assert(ptrheap);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;

}
//销毁堆的接口
void HeapDestroy(HP* ptrheap)
{
	assert(ptrheap);
	free(ptrheap->arry);
	ptrheap->arry = NULL;
	ptrheap->capacity = 0;
	ptrheap->size = 0;
}


//堆的打印接口
void HeapPrint(HP* ptrheap)
{
	assert(ptrheap);
	size_t tem = 0;
	for (tem = 0; tem < ptrheap->size; ++tem)
	{
		printf("%d->", ptrheap->arry[tem]);

	}
	printf("END\n");
}



//判断堆是否为空的接口
bool HeapEmpty(HP* ptrheap)
{
	assert(ptrheap);
	return (0 == ptrheap->size);
}


//返回堆元素个数的接口
size_t HeapSize(HP* ptrheap)
{
	assert(ptrheap);
	return ptrheap->size;
}




//返回堆顶元素的接口
HPDataType HeapTop(HP* ptrheap)
{
	assert(!HeapEmpty(ptrheap));
	return ptrheap->arry[0];
}





//元素交换接口
void Swap(HPDataType* e1, HPDataType* e2)
{
	assert(e1 && e2);
	HPDataType tem = *e1;
	*e1 = *e2;
	*e2 = tem;
}



//小堆元素的向上调整接口
void AdjustUp(HPDataType* arry, size_t child)  //child表示孩子结点的编号
{
	assert(arry);
	size_t parent = (child - 1) / 2;
	while (child > 0)						   //child减小到0时则调整结束
	{
		if (arry[child] < arry[parent])        //父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + child, arry+parent);
			child = parent;				//将原父结点作为新的子结点继续迭代过程
			parent = (child - 1) / 2;	//继续向上找另外一个父结点
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构任然成立,无需调整
		}
	}
}

// 插入一个小堆元素的接口
// 插入x以后，保持其数据结构依旧是小堆
void HeapPush(HP* ptrheap, HPDataType x)
{
	assert(ptrheap);
	if (ptrheap->capacity == ptrheap->size)	//容量检查,容量不够则扩容
	{
		size_t newcapacity = (0 == ptrheap->capacity) ? 4 : 2 * ptrheap->capacity;
		HPDataType* tem = (HPDataType*)realloc(ptrheap->arry, newcapacity * sizeof(HPDataType));
		assert(tem);
		ptrheap->arry = tem;
		ptrheap->capacity = newcapacity;
	}
	ptrheap->arry[ptrheap->size] = x;			//先尾插一个元素
	ptrheap->size++;
	//将尾插的元素进行向上调整以保持堆的数据结构
	AdjustUp(ptrheap->arry, ptrheap->size - 1); //根据完全二叉树的结构特点可知尾插进数组的元素在二叉树中编号为size-1
}



//小堆元素的向下调整接口
void AdjustDown(HPDataType* arry,size_t size,size_t parent)
{
	assert(arry);
	size_t child = 2 * parent + 1;   //确定父结点的左孩子的编号
	while (child < size)			 //child增加到大于或等于size时则调整结束
	{
		if (child + 1 < size && arry[child + 1] < arry[child]) //确定左右孩子中较小的孩子结点
		{
			++child;
		}
		if ( arry[child] < arry[parent])//父结点大于子结点,则子结点需要上调以保持小堆的结构
		{
			Swap(arry + parent, arry + child);
			parent = child;				//将原子结点作为新的父结点继续迭代过程
			child = 2 * parent + 1;		//继续向下找另外一个子结点
		}
		else
		{
			break;						//父结点不大于子结点,则堆结构任然成立,无需调整
		}
	}
}


//删除堆顶元素
void HeapPop(HP* ptrheap)
{
	assert(ptrheap);
	Swap(ptrheap->arry, ptrheap->arry + ptrheap->size - 1); //交换堆顶与堆尾元素
	ptrheap->size--;										//删除堆尾元素
	AdjustDown(ptrheap->arry, ptrheap->size, 0);			//将堆顶元素进行向下调整以保持堆的数据结构
}

我们只需将小根堆的堆元素上下调整算法接口中的子父结点值大小比较符号改为大于号即可实现大根堆

10.结语

  • 本文的核心:通过堆元素的上下调整算法接口完成堆的构建和删空(并分析过程的时间复杂度)
  • 堆元素上下调整算法接口在后续的堆排序和TopK问题中还会直接用到
  • 堆的高效性来源于如下数学思想:利用指数级展开的数据结构模型实现对数级回溯,从而降低了排序和查找的时间复杂度(不得不说前人的创造真的是无可比拟)

 

 

 

 

 

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/382138.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【chatgpt】教你如何创建一个Vue脚手架

【chatgpt】教你如何创建一个Vue脚手架

要创建一个Vue脚手架&#xff0c;您可以使用Vue CLI。Vue CLI是一个命令行工具&#xff0c;可帮助您快速创建Vue项目并提供开发环境。 以下是使用Vue CLI创建Vue脚手架的步骤&#xff1a; 首先&#xff0c;您需要安装Node.js。您可以在Node.js官网上下载和安装它。安装Vue CL…
阅读更多...
计网面试题-在浏览器中输入url地址到显示主页的过程

计网面试题-在浏览器中输入url地址到显示主页的过程

先说答案哈 1DNS解析( DNS解析就是把一个域名转换成一个IP地址。)1&#xff09;、先到浏览器的DNS缓存中查询是否有对应记录&#xff0c;如有则直接返回ip地址&#xff0c;完成解析&#xff0c;如果没有则下一步&#xff1b;2&#xff09;、继续查询本地host文件&#xff0c;…
阅读更多...
TIA博途中通过SCL语言实现快速排序的具体方法示例

TIA博途中通过SCL语言实现快速排序的具体方法示例

TIA博途中通过SCL语言实现快速排序的具体方法示例 首先，了解一下快速排序的原理： 排序算法的思想非常简单，在待排序的数列中，我们首先要找一个数字作为基准数。为了方便，我们一般选择第 1 个数字作为基准数（其实选择第几个并没有关系）。接下来我们需要将这个待排序的数列…
阅读更多...
Python开发之Python导包的几种方法，自定义包的生成以及导入详解

Python开发之Python导包的几种方法，自定义包的生成以及导入详解

Python是一种跨平台的计算机程序设计语言。 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。最初被设计用于编写自动化脚本(shell)&#xff0c;随着版本的不断更新和语言新功能的添加&#xff0c;越多被用于独立的、大型项目的开发。 下面介绍python的几种…
阅读更多...
网络协议---TCP和UDP

网络协议---TCP和UDP

文章目录TCPTCP简介内容TCP三次握手建立连接TCP四次挥手断开连接常见面试题TCP连接资源UDPUDP简介内容TCP TCP简介内容 传输控制协议&#xff08;TCP&#xff0c;Transmission Control Protocol&#xff09;是一种面向连接的、可靠的、基于字节流的传输层通信协议&#xff0c…
阅读更多...
MySQL-DQL语句

MySQL-DQL语句

DQL语句 DQL&#xff08;Data Query Language&#xff09;查询数据 操作查询&#xff1a;select简单的查询&#xff0c;复杂的查询数据库中最核心的语言&#xff0c;最重要的语句使用频繁的语句 指定查询 查询全部 语法&#xff1a; select 全部字段&#xff08;*&#x…
阅读更多...
全流程基于最新导则下的生态环境影响评价技术方法及图件制作与案例实践

全流程基于最新导则下的生态环境影响评价技术方法及图件制作与案例实践

根据最新生态环境影响评价导则&#xff0c;结合生态环评内容庞杂、综合性强的特点&#xff0c;以既包括陆域、又包括水域的项目为主要案例&#xff0c;对生态环评的具体流程及所需内容进行系统阐述。利用Rstudio、Fragstats等软件分析计算生态环评中所需各种指数&#xff0c;利…
阅读更多...
项目管理工具dhtmlxGantt甘特图入门教程（十五）：从MS项目导入/导出（下）

项目管理工具dhtmlxGantt甘特图入门教程（十五）：从MS项目导入/导出（下）

这篇文章给大家讲解dhtmlxGantt请求大文件导入的大小限制。 dhtmlxGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表&#xff0c;可满足应用程序的所有需求&#xff0c;是完善的甘特图图表库 DhtmlxGantt正版试用下载&#xff08;qun 764148812&#xff09;https:…
阅读更多...
【算法数据结构体系篇class10、11】：二叉树

【算法数据结构体系篇class10、11】：二叉树

一、二叉树的先序、中序、后序遍历先序&#xff1a;任何子树的处理顺序都是&#xff0c;先头节点、再左子树、然后右子树中序&#xff1a;任何子树的处理顺序都是&#xff0c;先左子树、再头节点、然后右子树后序&#xff1a;任何子树的处理顺序都是&#xff0c;先左子树、再右…
阅读更多...
基于tsfresh包的单类时间序列特征提取

基于tsfresh包的单类时间序列特征提取

前言 时间序列特征提取包中tsfresh较为流行&#xff0c;但是其官方教程给出的例子是机器人故障的数据集&#xff0c;其中的id列为各组不同的实验。然后我就一直在想能否做单类的&#xff0c;比如电力预测&#xff0c;或者是某一条街道的交通预测&#xff0c;但是翻遍了文档都没…
阅读更多...
Linux安装nginx详细步骤

Linux安装nginx详细步骤

1.安装依赖包//一键安装上面四个依赖yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel2.下载并解压安装包//创建一个文件夹 mkdir /usr/local/nginx cd /usr/local/nginx //下载tar包 wget http://nginx.org/download/nginx-1.18.0.tar.gz tar -xvf nginx…
阅读更多...
蓝牙调试工具集合汇总

蓝牙调试工具集合汇总

BLE 该部分主要分享一下常用的蓝牙调试工具&#xff0c;方便后续蓝牙抓包及分析。 目录 1 hciconfig 2 hcitool 3 hcidump 4 hciattach 5 btmon 6 bluetoothd 7 bluetoothctl 1 hciconfig 工具介绍&#xff1a;hciconfig&#xff0c;HCI 设备配置工具 命令格式&…
阅读更多...
金融行业数据模型

金融行业数据模型

一、Teradata FS-LDM Teradata 公司基于金融业务发布的FS-LDM&#xff08;Financial Servies Logical Data Model&#xff09; 十大主题&#xff1a;当事人、产品、协议、事件、资产、财务、机构、地域、营销、渠道。 1、当事人&#xff08;Party&#xff09; 银行所服务的任…
阅读更多...
学习.NET MAUI Blazor（七）、实现一个真正的ChatGPT聊天应用

学习.NET MAUI Blazor（七）、实现一个真正的ChatGPT聊天应用

今天在新闻上看到一条消息&#xff0c;OpenAI已经开放了ChatGPT的接口&#xff0c;也就是GPT-3.5&#xff0c;对比原来的GPT-3&#xff0c;增加了gpt-3.5-turbo、gpt-3.5-turbo-0301两个模型。 gpt-3.5-turbo&#xff1a;使用最新的GPT-3.5模型&#xff0c;并针对聊天进行了优…
阅读更多...
和风SDK查询城市ID（保姆级教程）

和风SDK查询城市ID（保姆级教程）

android studio版本&#xff1a;2021.2.1例程名&#xff1a;hfserachcityid这几天没什么事做&#xff0c;而且我原来那个“项目”因为免费api不能用了&#xff0c;只能改为和风的免费api,但需要申请&#xff0c;而且还要城市ID&#xff0c;玩天气的基本都知道城市ID这个东西&am…
阅读更多...
公司章程包括了哪些内容

公司章程包括了哪些内容

一、公司章程包括了哪些内容 《中华人民共和国公司法》第11条规定&#xff1a;“设立公司必须依法制定公司章程。公司章程对公司、股东、董事、监事、高级管理人员具有约束力。”明确地强调了公司章程对于公司的重要性&#xff0c;公司章程对于公司而言不但是股东合意达成的协…
阅读更多...
葵花8号卫星数据简介与下载笔记

葵花8号卫星数据简介与下载笔记

1、葵花8号卫星数据简介JMA于2015年7月7日开始运营Himawari-8&#xff0c;以取代MTSAT-2&#xff08;也称为Himawari-7&#xff09;。 Himawari-9号卫星于2017年3月10日开始后备运行。两颗卫星都位于向东约140.7度的轨道上&#xff0c;并将观测东亚和西太平洋区域15年。 源自Hi…
阅读更多...
【项目实战】IDEA常用快捷键汇总

【项目实战】IDEA常用快捷键汇总

一、修改为Eclipse的快捷键 相信很多朋友跟我一样&#xff0c; 都是习惯了eclipse的快捷键&#xff0c;没错&#xff0c;习惯这东西真的很难改&#xff01;IDEA非常强大&#xff0c;支持我们修改IDEA中的keymap为Eclipse的快捷键&#xff01;友好又贴心&#xff0c;有没有&…
阅读更多...
大数据框架之Hadoop：MapReduce（四）Hadoop数据压缩

大数据框架之Hadoop：MapReduce（四）Hadoop数据压缩

4.1概述 1、压缩概述 压缩技术能够有效减少底层存储系统&#xff08;HDFS&#xff09;读写字节数。压缩提高了网络带宽和磁盘空间的效率。在运行MR程序时&#xff0c;IO操作、网络数据传输、shuffle和Merge要花大量的时间&#xff0c;尤其是数据规模很大和工作负载密集的情况…
阅读更多...
3月2日第壹简报，星期四，农历二月十一

3月2日第壹简报，星期四，农历二月十一

3月2日第壹简报&#xff0c;星期四&#xff0c;农历二月十一坚持阅读&#xff0c;静待花开1. 第三次延期&#xff01;财政部&#xff1a;对于购置期在2023年的新能源汽车继续免征车辆购置税。2. 我国2月份制造业PMI为52.6% &#xff0c;创2012年4月以来新高。3. 全国地级市财力…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023