引言

上一节以高斯混合模型为引，简单介绍了狄利克雷过程($\text{Dirichlet Process,DP}$)。本节将通过公式推导描述标量参数$\alpha$的作用。

回顾：狄利克雷过程——基本介绍

狄利克雷过程本质上是分布的分布。基于给定的样本集合 X = { x ( i ) } i = 1 N \mathcal X= \{x^{(i)}\}_{i=1}^N X={x(i)}i=1N​，我们针对每个样本$x^{(i)}(i=1,2,\cdots ,N)$构建一个对应参数${\theta }^{(i)}(i=1,2,\cdots ,N)$。对应的参数集合$\theta$为：
θ = { θ ( i ) } i = 1 N \theta = \{\theta^{(i)}\}_{i=1}^N θ={θ(i)}i=1N​
关于狄利克雷过程，它的表达形式表示如下：
$$\mathcal{G}\sim \text{DP}[\alpha ,\mathcal{H}(\theta )]$$
其中$\mathcal{G}$是狄利克雷过程产生的样本结果，本身是一个离散分布($\text{Discrete Distribution}$)；$\mathcal{H}(\theta )$表示关于参数集合$\theta$的概率分布；$\alpha$则是一个调整分布结果$\mathcal{G}$离散程度的标量参数，且$\alpha >0$。

关于标量参数$\alpha$：

• 当$\alpha =0$时，此时的离散分布$\mathcal{G}$极度离散，无论如何随机采样，只能映射唯一的离散结果；
• 当$\alpha =\infty$时，此时离散分布$\mathcal{G}$在采样过程中，可能存在无穷多种离散结果提供选择，并且每种选择均存在对应的概率值。此时的$\mathcal{G}=\mathcal{H}(\theta )$。

下面会用公式推导的方式对上述两种情况进行描述。

狄利克雷过程——定义

根据上面的描述，如果分布$\mathcal{G}$是一个优秀的离散分布，那么从分布$\mathcal{G}$中产生的样本 θ ( i ) , θ ( j ) ( i , j ∈ { 1 , 2 , ⋯   , N } ; i ≠ j ) \theta^{(i)},\theta^{(j)}(i,j \in \{1,2,\cdots,N\};i \neq j) θ(i),θ(j)(i,j∈{1,2,⋯,N};i=j)必然存在${\theta }^{(i)}={\theta }^{(j)}$的情况发生。
也就是说,${\theta }^{(i)}={\theta }^{(j)}$意味着$x^{(i)},x^{(j)}$均指向了同一聚类信息。

此时，将不同结果的${\theta }^{(i)}$收集起来，其结果数量必然$<N$，$\theta$结果相同对应的样本子集${\mathcal{X}}_{\theta }$自然就聚类在一起，实现聚类数量$\mathcal{K}<N$的情况。
关于高斯混合模型的示例，详见狄利克雷过程——基本介绍

重新观察狄利克雷过程$\text{DP}(\alpha ,\mathcal{H})$，关于$\theta$的概率分布$\mathcal{H}(\theta )$被称作基本测度($\text{Base Measure}$)。从采样的角度观察狄利克雷过程与高斯混合模型，观察它们之间的区别：
作为区分，将$\varphi$作为高斯混合模型概率密度函数的参数。
$$\{\begin{array}{l}\mathcal{G}\sim \text{DP}(\alpha ,\mathcal{H})\\ x^{(j)}\sim \mathcal{P}(\mathcal{X};\varphi )\end{array}$$

能够发现：

• 从高斯混合模型中采样得到的结果是一个样本空间中的样本点；

• 从狄利克雷过程中采样得到的结果是一个完整分布，是一个随机离散型概率测度($\text{Random Discrete Probability Measure}$)。

  假设${\mathcal{G}}^{(i)}$是从$\text{DP}(\alpha ,\mathcal{H})$中采样得到的一个样本，那么离散分布${\mathcal{G}}^{(i)}$表示为如下形式：
  这里假设${\mathcal{G}}^{(i)}$是一个一维的分布
  $${\mathcal{G}}^{(i)}=\left(g_1^{(i)},g_2^{(i)},\cdots ,g_{\mathcal{K}}^{(i)}\right)\sum _{k=1}^{\mathcal{K}}{g}_k^{(i)}=1$$
  其中 g k ( i ) ( k ∈ { 1 , 2 , ⋯   , K } ) g_k^{(i)}(k \in \{1,2,\cdots,\mathcal K\}) gk(i)​(k∈{1,2,⋯,K})表示编号$k$离散结果的权重/概率信息。即便$\alpha$取值相同(${\alpha }_{same}$)，对应产生的随机离散分布${\mathcal{G}}^{(i)},{\mathcal{G}}^{(j)}(i\ne j;{\mathcal{G}}^{(i)},{\mathcal{G}}^{(j)}\sim \text{DP}({\alpha }_{same},\mathcal{H}))$也不相同，它们可能很相似。
  因而采样结果${\mathcal{G}}^{(i)}$也被称作‘随机测度’$(\text{Random Measure})$

  如果一维的随机离散分布${\mathcal{G}}^{(i)}$表示如下：
  
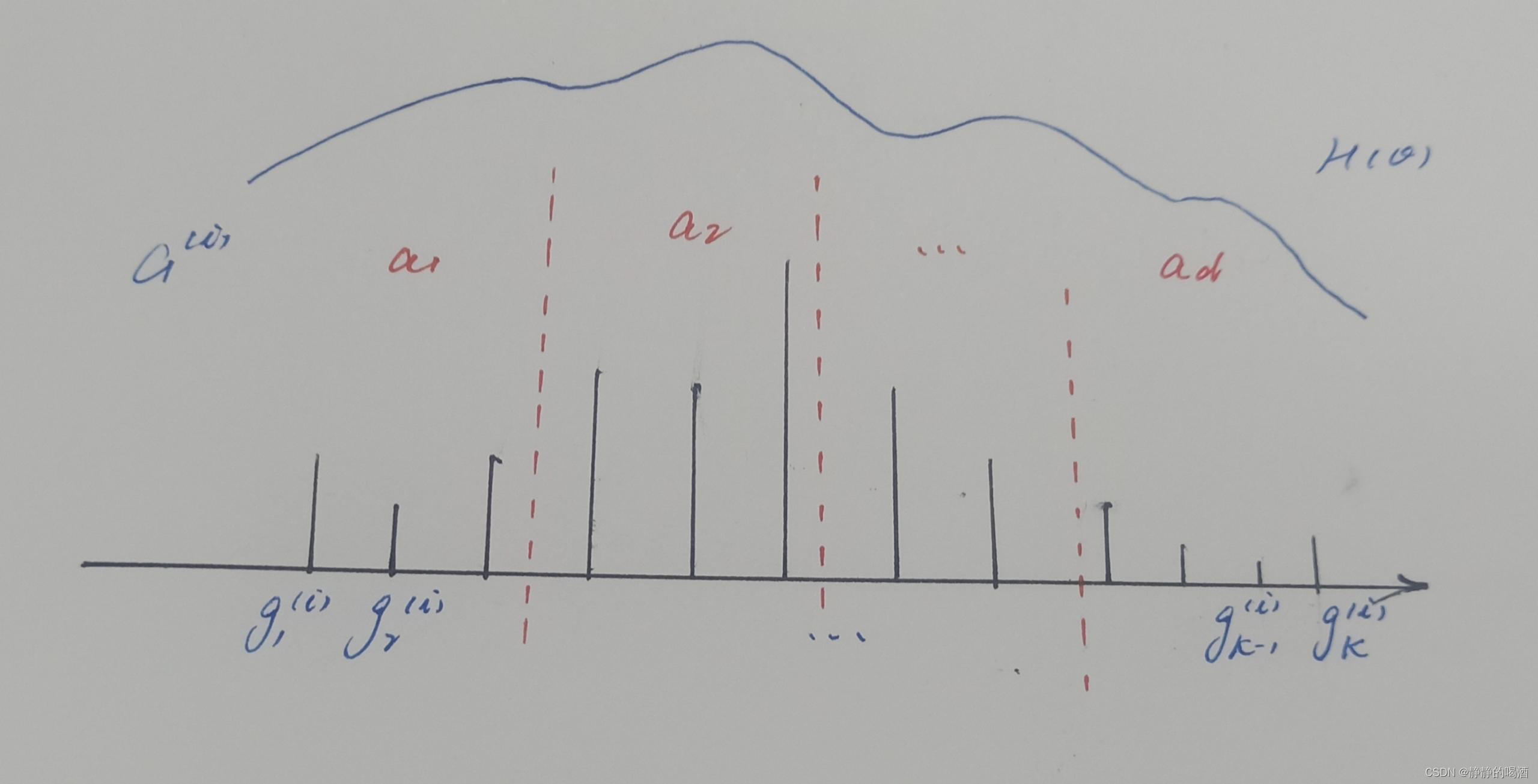
  观察该图像：

• 图像中的竖线表示离散分布${\mathcal{G}}^{(i)}$内对应的$\mathcal{K}$个离散结果的权重/概率信息。竖线越长，选择该离散结果的概率越大；

• 最上面的弧线表示$\mathcal{H}(\theta )$的概率分布，而${\mathcal{G}}^{(i)}$仅仅是基于$\mathcal{H}(\theta )$，给定$\alpha$条件下的一个随机离散测度样本。

• 将该随机离散分布结果划分成$\mathcal{D}$个区域： { a 1 , a 2 , ⋯   , a D } \{a_1,a_2,\cdots,a_{\mathcal D}\} {a1​,a2​,⋯,aD​}，每个区域内包含若干个权重结果。将这些权重结果的和作为该区域的权重信息。记作${\mathcal{G}}^{(i)}(a_d)$：
  $${\mathcal{G}}^{(i)}(a_d)=\sum _{g_k^{(i)}\in a_d}{g}_k^{(i)}$$
  至此，将${\mathcal{G}}^{(i)}$中的$\mathcal{K}$个权重结果划分为$\mathcal{D}$个区域，并得到$\mathcal{D}$个区域的权重信息：
  $${\mathcal{G}}^{(i)}(a_1),{\mathcal{G}}^{(i)}(a_2),\cdots ,{\mathcal{G}}^{(i)}(a_{\mathcal{D}})\sum _{d=1}^{\mathcal{D}}{\mathcal{G}}^{(i)}(a_d)=1$$
  虽然被划分成了$\mathcal{D}$个区域，但每个区域的权重信息 G ( i ) ( a d ) ( d ∈ { 1 , 2 , ⋯   , D } ) \mathcal G^{(i)}(a_d)(d \in \{1,2,\cdots,\mathcal D\}) G(i)(ad​)(d∈{1,2,⋯,D})依然是一个随机变量，并且${\mathcal{G}}^{(i)}(a_1),{\mathcal{G}}^{(i)}(a_2),\cdots ,{\mathcal{G}}^{(i)}(a_{\mathcal{D}})$同样是一个离散的概率分布。那么该分布需要服从的概率性质是 狄利克雷分布($\text{Dirichlet Distribution}$)
  $$[{\mathcal{G}}^{(i)}(a_1),{\mathcal{G}}^{(i)}(a_2),\cdots ,{\mathcal{G}}^{(i)}(a_{\mathcal{D}})]\sim \text{Dir}\left[\alpha \mathcal{H}(a_1),\alpha \mathcal{H}(a_2),\cdots ,\alpha \mathcal{H}(a_{\mathcal{D}})\right]$$
  其中 H ( a j ) ( j ∈ { 1 , 2 , ⋯   , D } ) \mathcal H(a_j)(j \in \{1,2,\cdots,\mathcal D\}) H(aj​)(j∈{1,2,⋯,D})表示被划分的$a_j$区域中的基本测度；$\alpha$与$\mathcal{H}(a_j)$的乘积$\alpha \mathcal{H}(a_j)$(标量)表示狄利克雷分布在$a_j$区域中的参数信息。

小插曲：狄利克雷分布的简单性质

假设随机变量集合$\mathcal{X}$包含$p$个随机变量：$\mathcal{X}\in {\mathbb{R}}^p$，并且概率分布$\mathcal{P}(\mathcal{X})=\mathcal{P}(x_1,x_2,\cdots ,x_p)$服从狄利克雷分布：
$$\mathcal{P}(x_1,x_2,\cdots ,x_p)\sim \text{Dir}({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_p)$$
其中${\alpha }_i(i=1,2,\cdots ,p)$表示各随机变量$x_i(i=1,2,\cdots ,p)$对应的参数。关于随机变量$x_i$的期望结果$\mathbb{E}[x_i]$与方差结果$\text{Var}[x_i]$分别表示为：
$$\{\begin{array}{l}\begin{array}{rl}\mathbb{E}[x_i]& =\frac{{\alpha }_i}{{\sum }_{k=1}^p{\alpha }_k}\\ \text{Var}[x_i]& =\frac{{\alpha }_i\cdot \left({\sum }_{k=1}^p{\alpha }_k-{\alpha }_i\right)}{{\left({\sum }_{k=1}^p{\alpha }_k\right)}^2\cdot \left(1+{\sum }_{k=1}^p{\alpha }_k\right)}\end{array}\end{array}$$

关于标量参数作用的推导过程

终上，简单总结狄利克雷过程的定义：

• 某一随机离散测度样本${\mathcal{G}}^{(i)}$服从标量参数$\alpha$、基本测度分布为$\mathcal{H}$的狄利克雷分布：
  $${\mathcal{G}}^{(i)}\sim \text{DP}(\alpha ,\mathcal{H})$$
• 假设将该分布样本${\mathcal{G}}^{(i)}=[g_1^{(i)},g_2^{(i)},\cdots ,g_{\mathcal{K}}^{(i)}{]}^T$划分成$\mathcal{D}$个区域$(a_1,a_2,\cdots ,a_{\mathcal{D}})$，并将每个区域中的权重信息求和，从而构成的新的分布：
  $$\underset{\text{Old Distribution}}{\underbrace{[g_1^{(i)},g_2^{(i)},\cdots ,g_{\mathcal{K}}^{(i)}{]}^T}}\Rightarrow \underset{\text{New Distribution}}{\underbrace{[{\mathcal{G}}^{(i)}(a_1),{\mathcal{G}}^{(i)}(a_2),\cdots ,{\mathcal{G}}^{(i)}(a_{\mathcal{D}}){]}^T}}$$
• 这个新分布服从对应参数为$\alpha \cdot \mathcal{H}(a_d)$的狄利克雷分布：
  $$[{\mathcal{G}}^{(i)}(a_1),{\mathcal{G}}^{(i)}(a_2),\cdots ,{\mathcal{G}}^{(i)}(a_{\mathcal{D}})]\sim \text{Dir}\left[\alpha \mathcal{H}(a_1),\alpha \mathcal{H}(a_2),\cdots ,\alpha \mathcal{H}(a_{\mathcal{D}})\right]$$

此时的随机变量是${\mathcal{G}}^{(i)}(a_d)(d=1,2,\cdots ,\mathcal{D})$，计算该随机变量的期望和方差结果：

• 其中$\alpha$是标量，并且不含$d$,可将其提到${\sum }_{d=1}^{\mathcal{D}}$前面.
• 并且${\sum }_{d=1}^{\mathcal{D}}\mathcal{H}(a_d)=1$是已知项。
  $$\begin{array}{rl}\mathbb{E}[{\mathcal{G}}^{(i)}(a_d)]& =\frac{\alpha \mathcal{H}(a_d)}{{\sum }_{d=1}^{\mathcal{D}}\alpha \mathcal{H}(a_d)}\\ & =\frac{\alpha \mathcal{H}(a_d)}{\alpha {\sum }_{d=1}^{\mathcal{D}}\mathcal{H}(a_d)}\\ & =\mathcal{H}(a_d)\end{array}$$

可以发现，分布样本${\mathcal{G}}^{(i)}$在$a_d$划分区域中的期望结果就是区域$a_d$的基本测度；并且这个期望结果$\mathbb{E}[{\mathcal{G}}^{(i)}(a_d)]$与标量参数$\alpha$无关。
仅需要将‘基本测度’$\mathcal{H}$看成一个概率密度函数(输出的是概率结果),$\mathcal{H}(a_d)=\mathcal{H}\left[{\sum }_{g_k^{(i)}\in a_d}{g}_k^{(i)}\right]$.

继续观察它的方差结果$\text{Var}\left[{\mathcal{G}}^{(i)}(a_d)\right]$：
套公式~
$$\begin{array}{rl}\text{Var}\left[{\mathcal{G}}^{(i)}(a_d)\right]& =\frac{\alpha \mathcal{H}(a_d)\cdot \left[\alpha \cdot {\sum }_{d=1}^{\mathcal{D}}\mathcal{H}(a_d)-\alpha \mathcal{H}(a_d)\right]}{{\left[\alpha \cdot {\sum }_{d=1}^{\mathcal{D}}\mathcal{H}(a_d)\right]}^2\cdot \left[\alpha \cdot {\sum }_{d=1}^{\mathcal{D}}\mathcal{H}(a_d)+1\right]}\\ & =\frac{\alpha \mathcal{H}(a_d)\cdot \left[\alpha -\alpha \mathcal{H}(a_d)\right]}{{\alpha }^2\cdot \left(\alpha +1\right)}\\ & =\frac{\mathcal{H}(a_d)[1-\mathcal{H}(a_d)]}{\alpha +1}\end{array}$$

• 首先观察当 标量参数$\alpha \to \infty$ 的情况下，此时无论是哪个区域$a_d(d=1,2,\cdots ,\mathcal{D})$，它对应${\mathcal{G}}^{(i)}(a_d)$的方差结果均为$0$，这意味着任意区域下下的随机测度${\mathcal{G}}^{(i)}(a_d)$均不存在方差噪声。它精准地等于$a_d$区域的基本测度$\mathcal{H}(a_d)$：
  即没有方差噪声地、精确地指向了期望的位置。
  $$\text{Var}\left[{\mathcal{G}}^{(i)}(a_d)\right]=0\iff {\mathcal{G}}^{(i)}(a_d)=\mathcal{H}(a_d)$$

• 相反，当 标量参数$\alpha =0$ 的情况下，$\text{Var}\left[{\mathcal{G}}^{(i)}(a_d)\right]=\mathcal{H}(a_d)[1-\mathcal{H}(a_d)]$。此时该方差是伯努利分布的方差结果。这意味着随机测度${\mathcal{G}}^{(i)}(a_d)$服从伯努利分布。

  而伯努利分布就是最简单的离散分布描述。当$\alpha =0$时，关于随机测度${\mathcal{G}}^{(i)}$内部某个权重$g_k^{(i)}$与某一区域$a_d$之间只有两种描述情况：

  • $g_k^{(i)}$属于$a_d$区域中的权重信息；
  • $g_k^{(i)}$不属于$a_d$区域中的权重信息；

下一节将从随机测度${\mathcal{G}}^{(i)}$生成过程的角度观察标量参数与分布离散程度的关系

相关参考：
徐亦达机器学习:Dirichlet-Process-part 2