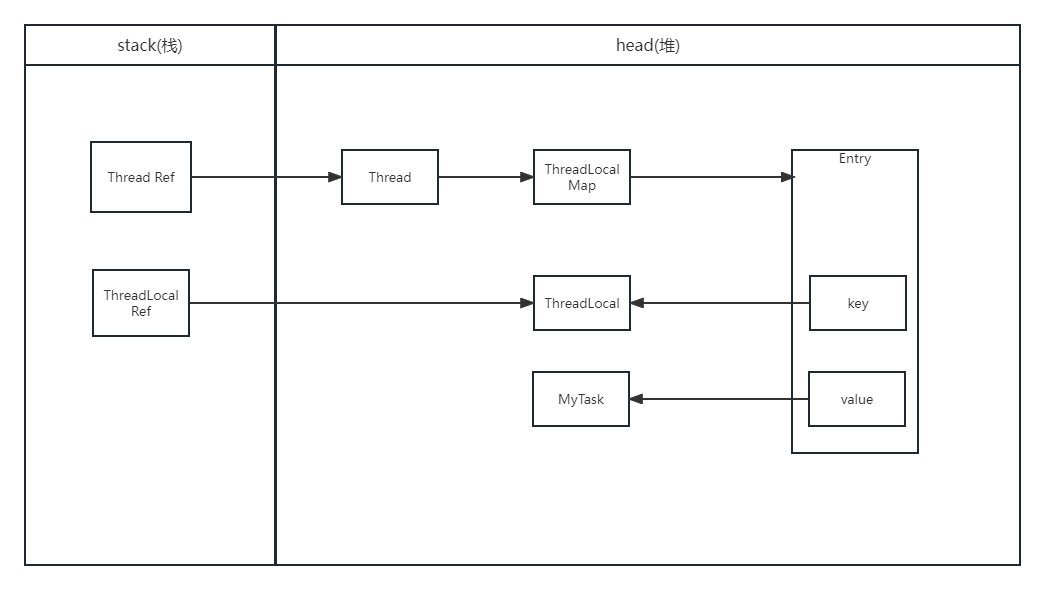
谷歌翻译无法使用，谷歌回应解释是，谷歌翻译使用率过低，所以选择停止服务。网上也有说法，指出根本原因为，提供API接口的googleapis被墙，这导致js文件和字体资源无法加载。

这里提供两种解决办法

方案一 修改hosts

此方案全局有效，idea上可以继续使用谷歌翻译，也可以在网页上使用谷歌翻译

主要是修改hosts文件，将谷歌翻译网址域名指向可用IP地址。

在hosts文件加入两行配置：

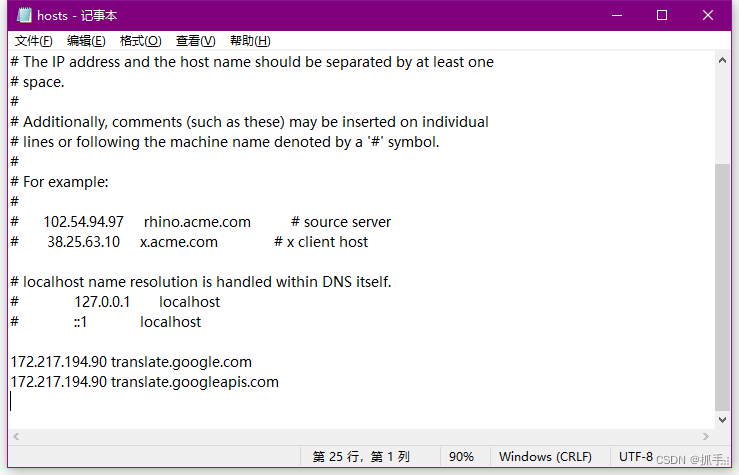
172.217.194.90 translate.google.com
172.217.194.90 translate.googleapis.com

hosts文件路径：C:\Windows\System32\drivers\etc\hosts 

 

其中IP 172.217.194.90可以通过下面两种方式获取：

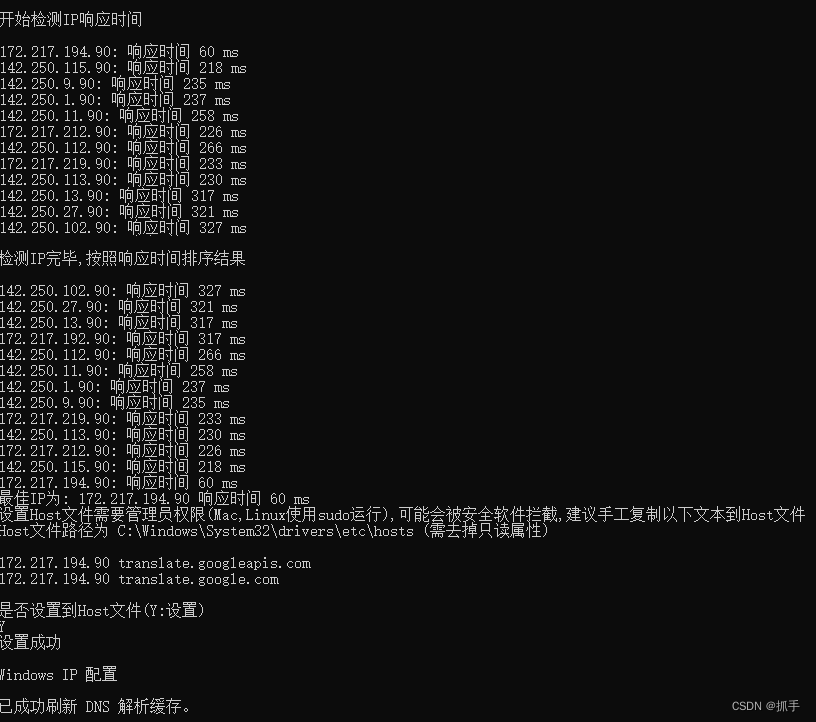
获取IP方式1

使用谷歌翻译hosts一键更改工具：GoogleTranslateIpCheck 1.6

工具地址：GitHub - Ponderfly/GoogleTranslateIpCheck

打不开GitHub，可以使用百度网盘地址：https://pan.baidu.com/s/195aSusNvAvMPywEsOiATsA  提取码：tw39 

解压后，使用管理员身份运行 GoogleTranslateIpCheck.exe 

获取IP方式2

进入网站：多个地点Ping服务器,网站测速 - 站长工具

在Ping检查一栏输入：translate.google.cn，查找IP，选择一个响应时间比较快的。

 

 

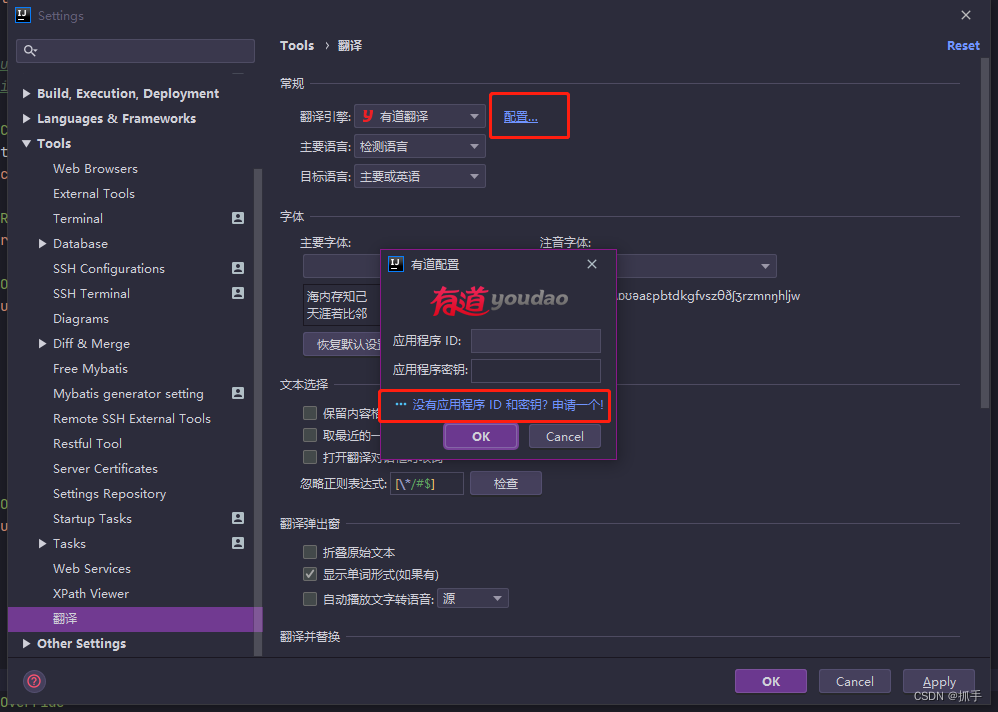
方案二 修改配置 切换翻译引擎

1.将翻译引擎换成有道翻译

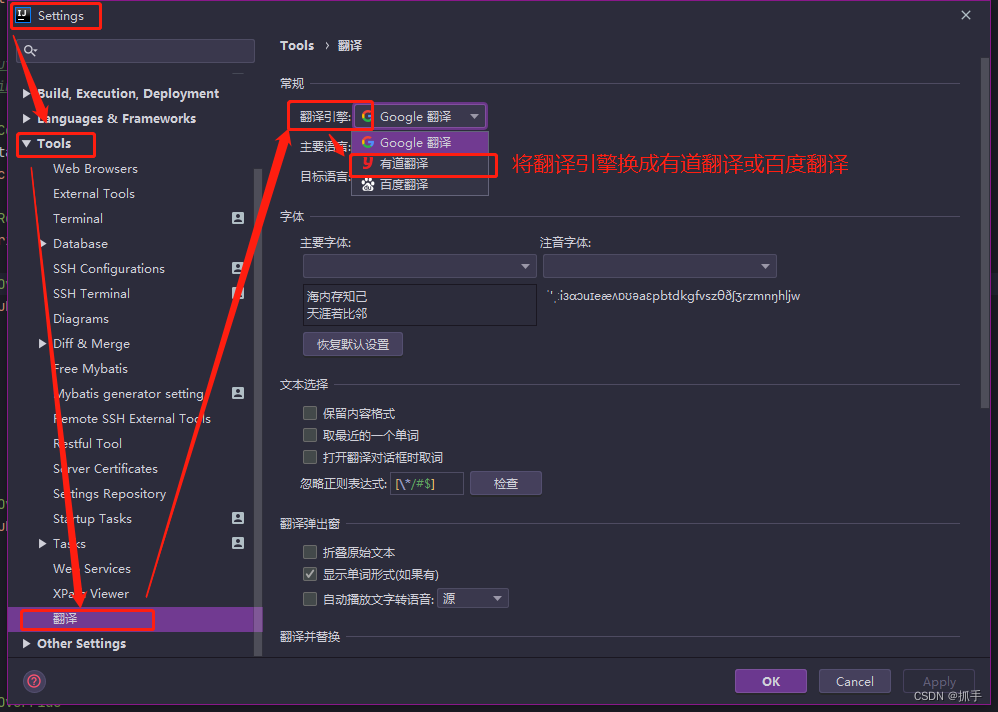
2.配置密钥