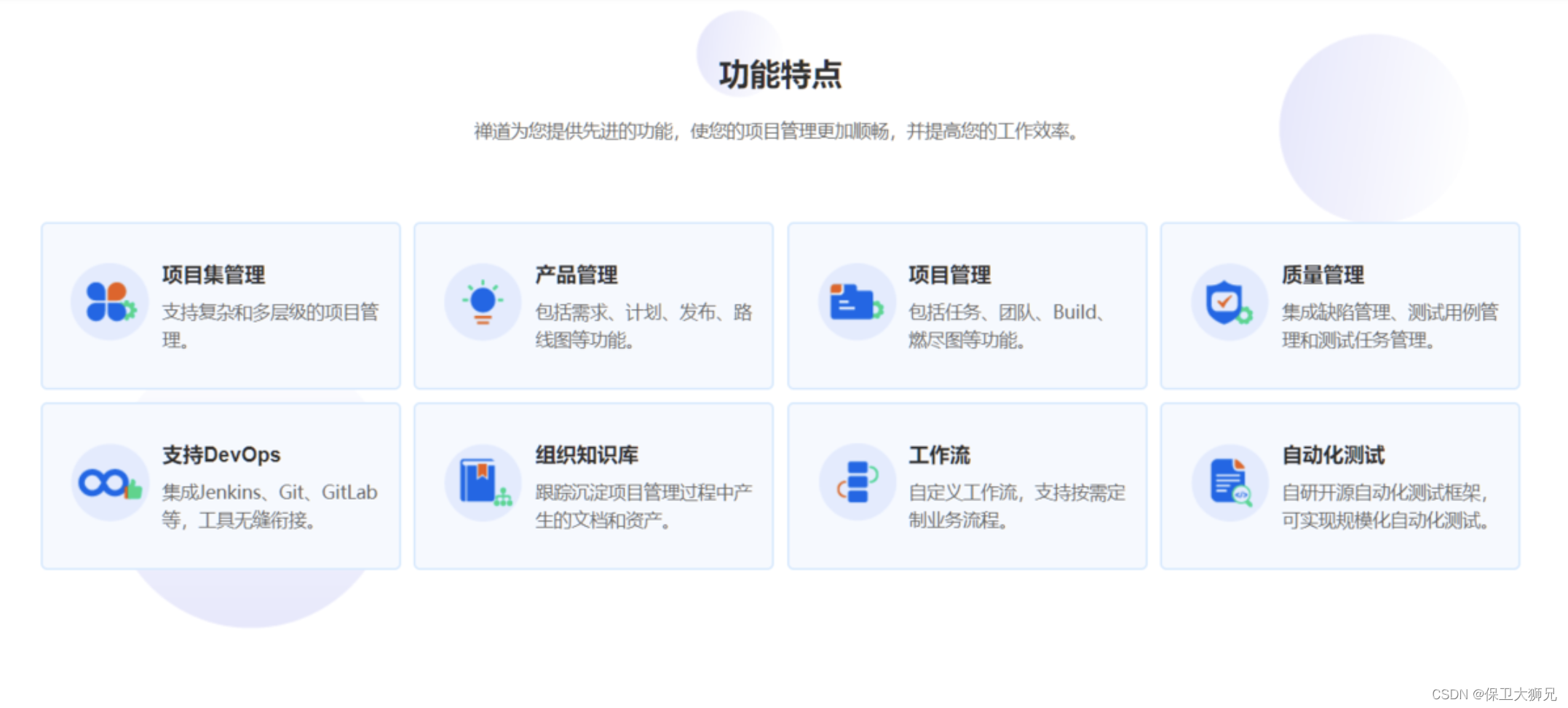
蓝桥杯-求和问题
- 1、问题描述
- 2、解法一:暴力解法(两层循环)
- 3、解法二:结合律(一层循环解决)
1、问题描述
给定 n 个整数 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,求它们两两相乘再相加的和,即:
S = a 1 . a 2 + a 1 . a 3 + . . . + a 1 . a n + a 2 . a 3 + . . . + a n − 2 . a n − 1 + + a n − 2 . a n + a n − 1 . a n S=a_1.a_2+a_1.a_3+...+a_1.a_n+a_2.a_3+...+a_{n-2}.a_{n-1}++a_{n-2}.a_{n}+a_{n-1}.a_n S=a1.a2+a1.a3+...+a1.an+a2.a3+...+an−2.an−1++an−2.an+an−1.an
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an 。
输出格式
输出一个整数 S,表示所求的和。请使用合适的数据类型进行运算。
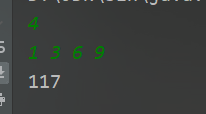
样例输入
4
1 3 6 9
样例输出
117
评测用例规模与约定
对于 30% 的数据,1≤n≤1000,1≤ a i a_i ai≤100 。
对于所有测评用例,1≤n≤200000,1≤ a i a_i ai≤1000。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
2、解法一:暴力解法(两层循环)
我们直接两个for循环就可以解决,每次遍历到某个数的额时候,让它与自己后面的所有数字相乘并求和即可。
以样例做个循环分析如下:
- i=0,j=1,2,3
- i=1,j=2,3
- i=2,j=3
代码如下:
// //暴力解法,这种会超时。
public static void sum1(){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] arr = new int[n];
long sum=0;
for (int i = 0; i < n; i++) {
int temp = scanner.nextInt();
arr[i]=temp;
}
for (int i = 0; i < arr.length; i++) {
for (int j =i+1; j <arr.length ; j++) {
sum+=arr[i]*arr[j];
}
}
System.out.println(sum);
scanner.close();
}
运行结果如下:
这种会超时,看下面这种优化后的。
3、解法二:结合律(一层循环解决)
根据结合律化简求和公式如下所示:
S
=
a
1
.
a
2
+
a
1
.
a
3
+
.
.
.
+
a
1
.
a
n
+
a
2
.
a
3
+
.
.
.
+
a
n
−
2
.
a
n
−
1
+
+
a
n
−
2
.
a
n
a
n
−
1
.
a
n
=
a
1
(
a
2
+
a
3
+
.
.
.
+
a
n
)
+
a
2
(
a
3
+
.
.
.
+
a
n
)
+
.
.
.
+
a
n
−
2
(
a
n
−
1
+
a
n
)
+
a
n
−
1
.
a
n
\begin{align} S & = a_1.a_2+a_1.a_3+...+a_1.a_n+a_2.a_3+...+a_{n-2}.a_{n-1}++a_{n-2}.a_{n}a_{n-1}.a_n \\ & = a_1(a_2+a_3+...+a_n)+a_2(a_3+...+a_n)+...+a_{n-2}(a_{n-1}+a_{n})+a_{n-1}.a_n \end{align}
S=a1.a2+a1.a3+...+a1.an+a2.a3+...+an−2.an−1++an−2.anan−1.an=a1(a2+a3+...+an)+a2(a3+...+an)+...+an−2(an−1+an)+an−1.an
如果输入为1 3 6 9
第一次两两相乘为1*3+1*6+1*9=1*(3+6+9)
第二次两两相乘为3*6+3*9=3*(+6+9)
第三次两两相乘为6*9=6*(9)
最后相加,即每一次该数乘以sum内不包含本身的值
代码如下所示:
public static void sum2(){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] arr = new int[n];
long sum=0;
long result=0;
for (int i = 0; i < n; i++) {
arr[i] = scanner.nextInt();
sum+=arr[i]; //直接刚开始就对数组求和
}
for (int i = 0; i <n; i++) {
sum=sum-arr[i];
result+=arr[i]*sum;
}
System.out.println(result);
}

这里sum必须用long类型,要不会超出int范围