红黑树讲解和实现
- 1 红黑树介绍
- 1.1 红黑树特性
- 1.2 红黑树的插入
- 1.3 红黑树的删除
- 2 完整代码实现
- 2.1 rtbtree.h头文件
- 2.2 main.c源文件
1 红黑树介绍
红黑树( Red-Black tree,简称RB树)是一种自平衡二叉查找树,是计算机科学中常见的一种数据结构,其典型用途是实现关联数组。红黑树的结构复杂,但其操作有着良好的最坏情况运行时间,且在实践中有着较高的效率:它可以在O(log2n)时间内完成查找、插入和删除操作,其中的n是树中结点的数量。
红黑树(RB树)是二叉树中重要的知识点,因为在操作系统的内核中、C++的STL和Java的数据结构中都大量使用了红黑树,红黑树的增删查改的复杂度均为log2n。
1.1 红黑树特性
红黑树是每个结点都带有颜色属性的二叉查找树,颜色为红色或黑色,给结点进行染色的原因是用颜色和红黑树性质对树进行平衡,使得红黑树的任意一条路径长度都不可能超过其他路径的两倍。在二叉查找树的–般要求以外,对于任何有效的红黑树,我们额外增加了如下性质:
- 结点是红色的或黑色的。
- 根是黑色的。
- 所有叶子结点都是黑色的(叶子是NIL结点)。
- 每个红色结点必须有两个黑色的子结点(从每个叶子到根的所有路径上不能有两个连续的红色结点)。
- 从任意一个点到其每个叶子的所有简单路径都包含相同数量的黑色结点。
王道408考研的咸鱼学长总结了一个口诀:左根右、根叶黑、不红红、黑路同。
1.2 红黑树的插入
红黑树的插入结点,首先标记为红色,按照二叉排序树的方式插入后再做调整。红黑树的插入分为5种情况。
**情形一:**新结点N是树根没有子节点。这种空树的情况,直接将新结点作为根插入染成黑色即可。具体代码如下:
void insert_case1(node *n)
{
if(n->parent == NULL)//如果新插入结点没有父结点,即此结点为根结点
n->color = BLACK;//直接染黑
else
insert_case2(n);//否则转入情形2,即有父结点的情况
}
**情形二:**父结点为黑色,则直接将新结点插入,满足性质四不红红(即没有两个连续红色)。还满足性质5,不会增减该路径上黑色结点的数量。具体代码如下:
void insert_case2(node *n)
{
if(n->parent->color == BLACK) //如果父结点为黑色,则直接插入
return; //不需要调整
else
insert_case3(n); //如果父结点为红色,则需要调整
}
**情形三:**如果父结点和叔结点都是红色的,那么我们可以将父结点和叔结点都染黑(保证不红红性质4),然后将爷结点染红,插入的子结点仍然是红色(满足路黑同性质5)。此时需要考虑爷结点是否为根结点,如果爷结点为根结点,则需要将爷结点染黑,保证性质不变,如果爷结点不为根结点,则向上将爷结点(红)作为其父结点的新插入结点,递归情形一。下面给出图示和实现代码:
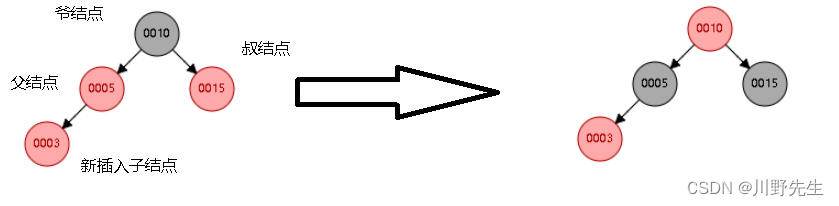
void insert_case3(node *n)
{
if(uncle(n)!=NULL && uncle(n)->color == RED && n->parent->color == RED){//这里父结点颜色可以不考虑,否则违反黑路同性质5,为了和算法描述一致,也加入判断
n->parent->color = BLACK;//将父结点染黑
uncle(n)->color = BLACK;//将叔结点染黑
grandparent(n)->color = RED;//将爷结点染红
insert_case1(grandparent(n));//将红色的爷结点作为新结点,对上级进行调整
}
else
insert_case4(n);//不满足情形3,则考虑情形4
}
**情形四:**父结点是红色,叔结点是黑色或者缺少的情况,并且新结点是父结点的右子节点,而父结点又是爷结点的左子节点。这种情况需要左旋调换新结点和父结点。
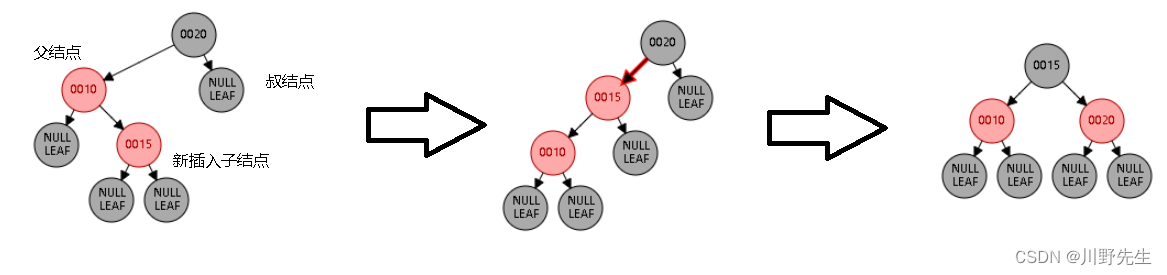
void insert_case4(node *n)
{
if(n == n->parent->right && n->parent == grandparent(n)->left){
roate_left(n->parent);
n = n->left;
}
else if(n->parent->left && n->parent == grandparent(n)->right){
rotate_right(n->parent);//上图中对称的情况父结点在爷结点右边,子结点在父结点左边
n = n->right;
}
insert_case5(n);//情形5
}
**情形五:**父结点是红色,叔结点是黑色或缺少,子结点是父节点的左子节点,而父结点又是爷结点的左下结点。这种情况需要将爷结点右旋,并且改变相应结点的颜色完成插入。
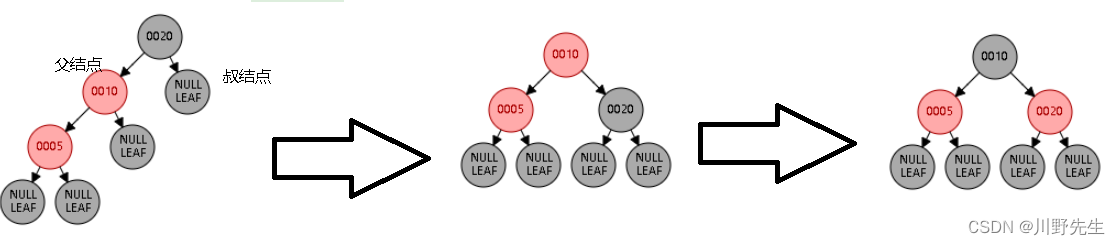
void insert_case5(node *n)
{
n->parent->color = BLACK;
grandparent(n)->color = RED;
if(n->parent->left == n && n->parent == grandparent(n)->left){
rotate_right(grandparent(n));
}
else if(n->parent->right == n && n->parent == grandparent(n)->right){
//与上图中完全对称的情况
rotate_left(grparent(n);
}
}
插入修正函数: 对于上述情景3、4、5,红黑树插入结点后,可能会失去平衡,调用此函数保持性质。对于下图中情形三可以单独处理,而情形四可以通过旋转到情形五,进而调整。
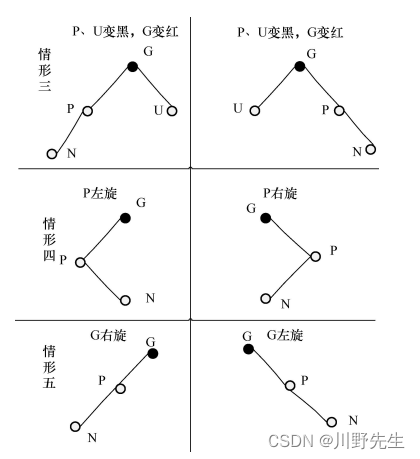
static void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node *parent,*gparent;
//如果父结点存在且为红色需要调整
while((parent = rb_parent(node)) && rb_is_red(parent)){
gparent = rb_parent(parent);
//若父结点是爷结点的左孩子结点
if(parent == gparent->left){
//情况1条件:叔结点存在且为红色,这种是情形3
Node *uncle = gparent->right;
if(uncle && rb_is_red(uncle)){
//将父结点和叔结点染黑,将爷结点染红
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;//node调整完毕,回到父结点
}
}
//情况2条件:叔结点是黑色或不存在,且当前结点是父节点的有孩子,情形4
//父节点右旋,交换父子结点
if (parent->right == node){
Node *tmp;
rbtree_left_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
//情形3条件:叔结点是黑色,且当前结点是父节点的左孩子结点。这里是情形 5
rb_set_black(parent); //旋转前设置好颜色
rb_set_red(gparent); //旋转前设置好颜色
rbtree_right_rotate(root, gparent);//爷结点右旋
}
else{//若父结点是祖父结点的右孩子结点,则下面三种和上面的是对称的
Node *uncle = gparent->left;
if (uncle && rb_is_red(uncle)){
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue; //继续进行调整
}
if (parent->left == node){
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
//Case 3 条件:叔父结点是黑色的,且当前结点是右孩子结点。这里是情形 5
rb_set_black(parent); //旋转前设置好颜色
rb_set_red(gparent); //旋转前设置好颜色
rbtree_left_rotate(root, gparent);
}
//将根结点设为黑色
rb_set_black(root->node);
}
1.3 红黑树的删除
&emps;&emps;对于红黑树的删除中,考虑删除结点为黑色或红色,如果删除结点为红色则不需要做调整,正常删除,因为删除红色结点不会影响黑高。而删除黑色结点则比较复杂,需要考虑以下六种情形。
**注意:**接下来的删除讲解均按照此图进行,此图是指删除结点后红黑树,删除规则按照二叉平衡树的方式,之后未作其他的调整。我们把删除结点N后的替代的结点记为X。
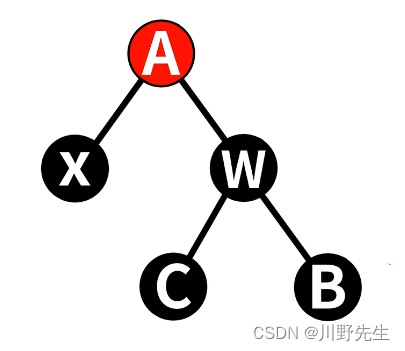
情形一: 红黑树仅有一个黑根,删除此根满足所有性质。代码如下:
void delete_case1(struct node *n)
{
if(n->parent!=NULL)
delete_case2(n);//如果删除的结点不是根
}
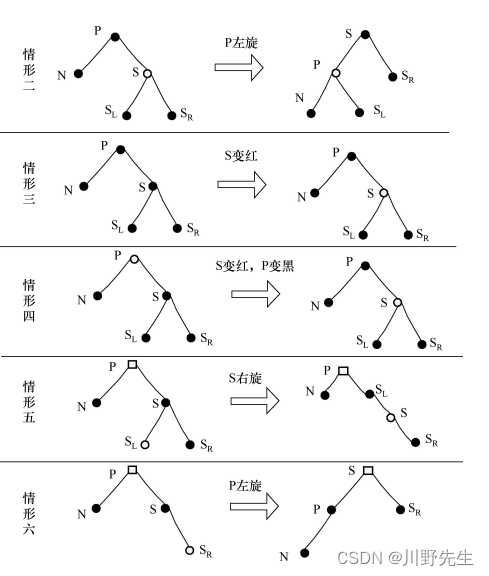
情形二: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的兄弟结点W结点是红色。这种删除的情况会使左边黑高-1,破坏了黑路同性质5,所以需要做染色左旋操作。先将父结点染红,再将兄弟结点W染黑,然后对父结点进行左旋操作,这样不会破坏红黑树的性质。
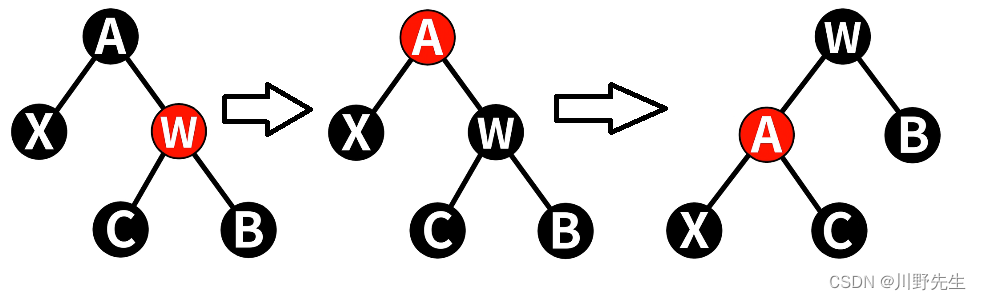
void delete_case2(struct node *n)
{
struct node *s = sibling(n);//n的兄弟结点
if(s->color == RED){//如果兄弟结点是红色
n->parent->color = RED;//将父结点染红
s->color = BLACK;//将父结点染黑
if(n->parent->left == n)//如果n是左孩子
rotate_ left(n->parent);//父结点左旋
else //如果n是右孩子
rotate_right(n->parent);//父结点右旋
}
delete_case3(n);//考虑情景3
}
情形三: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的父结点、兄弟结点W及其子结点均为黑色。左侧黑高-1,破坏了黑路同性质5,此时将兄弟结点W染红,使得满足黑路同性质5,但是如果A树作为左子树或者右子树,整体黑高-1,此时需要将矛盾上移,在A结点上重新做平衡处理。代码如下:
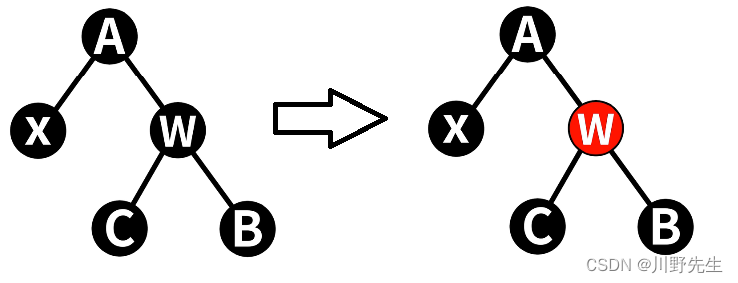
void delete_case3(struct node *n)
{
struct node *s = sibling(n);
if((n->parent->color == BLACK) && (S->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)){
s->color = RED;//将兄弟结点染红
delete_case1(n->parent);//将父结点作为新的处理结点,从case1开始平衡
}
else
delete_case4(n);//如果不符合情形三,请看情形4
}
**情形四:**被删除的黑色结点N,黑色结点X是N的顶替结点,父结点A是红色,兄弟结点W及其子结点都是黑色。此时左侧黑高-1,不满足黑路同性质5,所以需要调整,将父结点A染黑,兄弟结点W染红,则满足性质。代码如下:
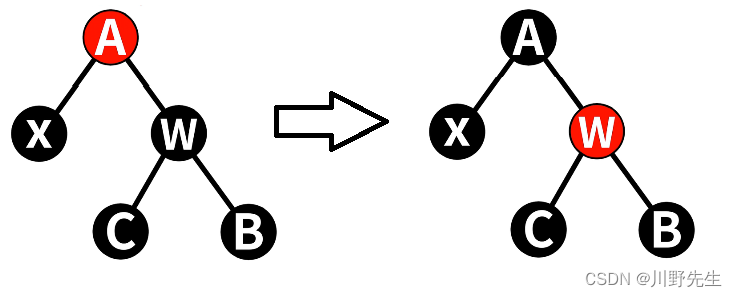
void delete_case4(struct node *n)
{
struct node *s = sibling(n);
if((n->parent->color == RED) && (S->color == BLACK) && (s->left->color == BLACK) && (s->right->color == BLACK)){
s->color = RED;//将兄弟结点染红
n->parent = BLACK;//将父结点染黑
}
else
delete_case5(n);//如果不符合情形4,考虑情形五
}
情形五: 被删除的黑色结点N,黑色结点X是N的顶替结点,X的兄弟结点W是黑色,W结点的左子结点是红色,W结点的右子结点是黑色。此时将兄弟结点W染红,W的左子结点染黑,然后进行右旋操作,此时代替结点X和父结点A都不受右旋影响。然后继续情形六。代码如下:

void
delete_case5(struct node *n)
{
struct node *s = sibling (n);
if(s->color == BLACK){
if((n == n->parent->left)&&(s->right->color == BLACK)&&(s->left->color == RED)) {
// 这种情况下 n 结点是其父结点的左子结点,S 结点是其父结点的右子结
s->color = RED;
s->left->color = BLACK;
rotate_right (s);
}
else if((n == n->parent->right)&&(s->left->color == BLACK)&&(s->right->color == RED)) {
// 这种情况下 n 结点是其父结点的右子结点,S 结点是其父结点的左子结点
s->color = RED;
s->right->color = BLACK;
rotate_left (s);
}
}
delete_case6 (n); //调整完毕后,再通过情形 6 进行调整
}
情形六: 被删除的黑色结点N,黑色结点X是N的顶替结点,兄弟结点W结点是黑色的,W结点的右子结点是红色的,而替代结点X是其父结点A的左子结点。将兄弟结点W染红,将父结点A染黑,W的右子结点也染黑,然后W左旋操作。就达到了情形四的情况。代码如下:
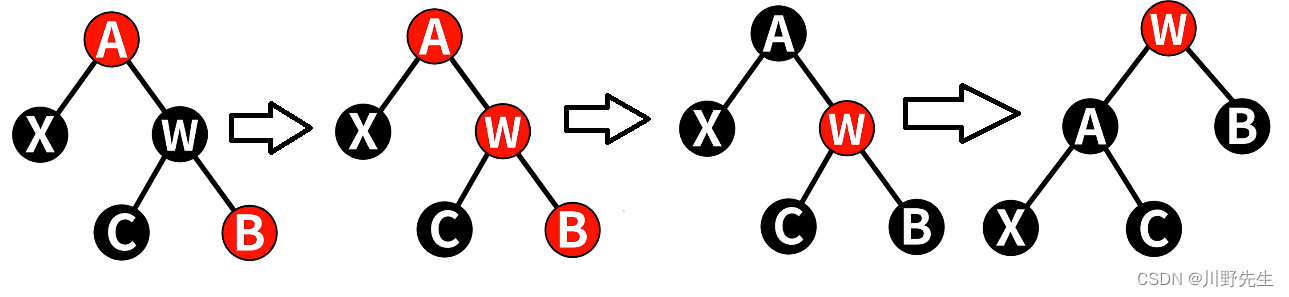
void delete_case6(struct node *n)
{
struct node *s = sibling(n);
s->color = n->parent->color;
n->parent->color = BLACK;
if(n->parent->left==n){
s->right->color = BLACK;
rotate_left(n->parent);
}
else{
s->left->color = BLACK;
rotate_right(n->parent);
}
}
删除修正函数:
static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
{
Node *other;
//下面的x说的是node
while ((!node || rb_is_black(node)) && node != root->node)
{
if (parent->left == node)
{
//删除
other = parent->right;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的,删除77
rb_set_black(other);
rb_set_red(parent);
rbtree_left_rotate(root, parent);
other = parent->right;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除65时,删除82时,二级进入循环
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->right || rb_is_black(other->right))
{
// Case 3: x的兄弟w是黑色的,并且w的右孩子为黑色。
rb_set_black(other->left);
rb_set_red(other);
rbtree_right_rotate(root, other);
other = parent->right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->right);
rbtree_left_rotate(root, parent);
node = root->node;
break;
}
}
else
{//删除
other = parent->left;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
rbtree_right_rotate(root, parent);
other = parent->left;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除77
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->left || rb_is_black(other->left))
{
//删除99时,应该是w的左孩子是黑色
// Case 3: x的兄弟w是黑色的,并且w的左孩子是为黑色。
rb_set_black(other->right);
rb_set_red(other);
rbtree_left_rotate(root, other);
other = parent->left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->left);
rbtree_right_rotate(root, parent);
node = root->node;
break;
}
}
}
if (node)
rb_set_black(node);
}
2 完整代码实现
2.1 rtbtree.h头文件
#ifndef _RED_BLACK_TREE_H_
#define _RED_BLACK_TREE_H_
#define RED 0 // 红色节点
#define BLACK 1 // 黑色节点
typedef int Type;
// 红黑树的节点
typedef struct RBTreeNode{
unsigned char color; // 颜色(RED 或 BLACK)
Type key; // 关键字(键值)
struct RBTreeNode *left; // 左孩子
struct RBTreeNode *right; // 右孩子
struct RBTreeNode *parent; // 父结点
}Node, *RBTree;
// 红黑树的根
typedef struct rb_root{
Node *node;
}RBRoot;
// 创建红黑树,返回"红黑树的根"!
RBRoot* create_rbtree();
// 销毁红黑树
void destroy_rbtree(RBRoot *root);
// 将结点插入到红黑树中。插入成功,返回0;失败返回-1。
int insert_rbtree(RBRoot *root, Type key);
// 删除结点(key为节点的值)
void delete_rbtree(RBRoot *root, Type key);
// 前序遍历"红黑树"
void preorder_rbtree(RBRoot *root);
// 中序遍历"红黑树"
void inorder_rbtree(RBRoot *root);
// 后序遍历"红黑树"
void postorder_rbtree(RBRoot *root);
// (递归实现)查找"红黑树"中键值为key的节点。找到的话,返回0;否则,返回-1。
int rbtree_search(RBRoot *root, Type key);
// (非递归实现)查找"红黑树"中键值为key的节点。找到的话,返回0;否则,返回-1。
int iterative_rbtree_search(RBRoot *root, Type key);
// 返回最小结点的值(将值保存到val中)。找到的话,返回0;否则返回-1。
int rbtree_minimum(RBRoot *root, int *val);
// 返回最大结点的值(将值保存到val中)。找到的话,返回0;否则返回-1。
int rbtree_maximum(RBRoot *root, int *val);
// 打印红黑树
void print_rbtree(RBRoot *root);
#endif
2.2 main.c源文件
/**
* C语言实现的红黑树(Red Black Tree)
*
* @author skywang
* @date 2013/11/18
*/
#include <stdio.h>
#include <stdlib.h>
#include "rbtree.h"
#define rb_parent(r) ((r)->parent)
#define rb_color(r) ((r)->color)
#define rb_is_red(r) ((r)->color==RED)
#define rb_is_black(r) ((r)->color==BLACK)
#define rb_set_black(r) do { (r)->color = BLACK; } while (0)
#define rb_set_red(r) do { (r)->color = RED; } while (0)
#define rb_set_parent(r,p) do { (r)->parent = (p); } while (0)
#define rb_set_color(r,c) do { (r)->color = (c); } while (0)
/*
* 创建红黑树,返回"红黑树的根"!
*/
RBRoot* create_rbtree()
{
RBRoot *root = (RBRoot *)malloc(sizeof(RBRoot));
root->node = NULL;
return root;
}
/*
* 前序遍历"红黑树"
*/
static void preorder(RBTree tree)
{
if(tree != NULL)
{
printf("%d ", tree->key);
preorder(tree->left);
preorder(tree->right);
}
}
void preorder_rbtree(RBRoot *root)
{
if (root)
preorder(root->node);
}
/*
* 中序遍历"红黑树"
*/
static void inorder(RBTree tree)
{
if(tree != NULL)
{
inorder(tree->left);
printf("%d ", tree->key);
inorder(tree->right);
}
}
void inorder_rbtree(RBRoot *root)
{
if (root)
inorder(root->node);
}
/*
* 后序遍历"红黑树"
*/
static void postorder(RBTree tree)
{
if(tree != NULL)
{
postorder(tree->left);
postorder(tree->right);
printf("%d ", tree->key);
}
}
void postorder_rbtree(RBRoot *root)
{
if (root)
postorder(root->node);
}
/*
* (递归实现)查找"红黑树x"中键值为key的节点
*/
static Node* search(RBTree x, Type key)
{
if (x==NULL || x->key==key)
return x;
if (key < x->key)
return search(x->left, key);
else
return search(x->right, key);
}
int rbtree_search(RBRoot *root, Type key)
{
if (root)
return search(root->node, key)? 0 : -1;
}
/*
* (非递归实现)查找"红黑树x"中键值为key的节点
*/
static Node* iterative_search(RBTree x, Type key)
{
while ((x!=NULL) && (x->key!=key))
{
if (key < x->key)
x = x->left;
else
x = x->right;
}
return x;
}
int iterative_rbtree_search(RBRoot *root, Type key)
{
if (root)
return iterative_search(root->node, key) ? 0 : -1;
}
/*
* 查找最小结点:返回tree为根结点的红黑树的最小结点。
*/
static Node* minimum(RBTree tree)
{
if (tree == NULL)
return NULL;
while(tree->left != NULL)
tree = tree->left;
return tree;
}
int rbtree_minimum(RBRoot *root, int *val)
{
Node *node;
if (root)
node = minimum(root->node);
if (node == NULL)
return -1;
*val = node->key;
return 0;
}
/*
* 查找最大结点:返回tree为根结点的红黑树的最大结点。
*/
static Node* maximum(RBTree tree)
{
if (tree == NULL)
return NULL;
while(tree->right != NULL)
tree = tree->right;
return tree;
}
int rbtree_maximum(RBRoot *root, int *val)
{
Node *node;
if (root)
node = maximum(root->node);
if (node == NULL)
return -1;
*val = node->key;
return 0;
}
/*
* 找结点(x)的后继结点。即,查找"红黑树中数据值大于该结点"的"最小结点"。
*/
static Node* rbtree_successor(RBTree x)
{
// 如果x存在右孩子,则"x的后继结点"为 "以其右孩子为根的子树的最小结点"。
if (x->right != NULL)
return minimum(x->right);
// 如果x没有右孩子。则x有以下两种可能:
// (01) x是"一个左孩子",则"x的后继结点"为 "它的父结点"。
// (02) x是"一个右孩子",则查找"x的最低的父结点,并且该父结点要具有左孩子",找到的这个"最低的父结点"就是"x的后继结点"。
Node* y = x->parent;
while ((y!=NULL) && (x==y->right))
{
x = y;
y = y->parent;
}
return y;
}
/*
* 找结点(x)的前驱结点。即,查找"红黑树中数据值小于该结点"的"最大结点"。
*/
static Node* rbtree_predecessor(RBTree x)
{
// 如果x存在左孩子,则"x的前驱结点"为 "以其左孩子为根的子树的最大结点"。
if (x->left != NULL)
return maximum(x->left);
// 如果x没有左孩子。则x有以下两种可能:
// (01) x是"一个右孩子",则"x的前驱结点"为 "它的父结点"。
// (01) x是"一个左孩子",则查找"x的最低的父结点,并且该父结点要具有右孩子",找到的这个"最低的父结点"就是"x的前驱结点"。
Node* y = x->parent;
while ((y!=NULL) && (x==y->left))
{
x = y;
y = y->parent;
}
return y;
}
/*
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋):
* px px
* / /
* x y
* / \ --(左旋)--> / \ #
* lx y x ry
* / \ / \
* ly ry lx ly
*
*
*/
static void rbtree_left_rotate(RBRoot *root, Node *x)
{
// 设置x的右孩子为y
Node *y = x->right;
// 将 “y的左孩子” 设为 “x的右孩子”;
// 如果y的左孩子非空,将 “x” 设为 “y的左孩子的父亲”
x->right = y->left;
if (y->left != NULL)
y->left->parent = x;
// 将 “x的父亲” 设为 “y的父亲”
y->parent = x->parent;
if (x->parent == NULL)//修改红黑树的根节点
{
//tree = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
root->node = y; // 如果 “x的父亲” 是空节点,则将y设为根节点
}
else
{
if (x->parent->left == x)
x->parent->left = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
else
x->parent->right = y; // 如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子”
}
// 将 “x” 设为 “y的左孩子”
y->left = x;
// 将 “x的父节点” 设为 “y”
x->parent = y;
}
/*
* 对红黑树的节点(y)进行右旋转
*
* 右旋示意图(对节点y进行左旋):
* py py
* / /
* y x
* / \ --(右旋)--> / \ #
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
static void rbtree_right_rotate(RBRoot *root, Node *y)
{
// 设置x是当前节点的左孩子。
Node *x = y->left;
// 将 “x的右孩子” 设为 “y的左孩子”;
// 如果"x的右孩子"不为空的话,将 “y” 设为 “x的右孩子的父亲”
y->left = x->right;
if (x->right != NULL)
x->right->parent = y;
// 将 “y的父亲” 设为 “x的父亲”
x->parent = y->parent;
if (y->parent == NULL)
{
//tree = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
root->node = x; // 如果 “y的父亲” 是空节点,则将x设为根节点
}
else
{
if (y == y->parent->right)
y->parent->right = x; // 如果 y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
else
y->parent->left = x; // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
}
// 将 “y” 设为 “x的右孩子”
x->right = y;
// 将 “y的父节点” 设为 “x”
y->parent = x;
}
/*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* root 红黑树的根
* node 插入的结点 // 对应《算法导论》中的z
*/
static void rbtree_insert_fixup1(RBRoot *root, Node *node)
{
Node *parent, *gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while ((parent = rb_parent(node)) && rb_is_red(parent))
{
gparent = rb_parent(parent);
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent->left)
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->right;
if (uncle && rb_is_red(uncle))//没有节点进入该分支,如何构造?
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子,叔叔不存在,也认为是黑色
if (parent->right == node)//插入80节点时,先左旋,后右旋
{
Node *tmp;
rbtree_left_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
rb_set_black(parent);//旋转前设置好颜色
rb_set_red(gparent);//旋转前设置好颜色
rbtree_right_rotate(root, gparent);
}
else//若父节点是祖父节点的右孩子
{
// Case 1条件:叔叔节点是红色
{
Node *uncle = gparent->left;//当插入60时,调整颜色即可,调整颜色后不符合红黑树,递归进行
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;//继续进行调整
}
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子,插入30时,先右旋,后左旋
if (parent->left == node)
{
Node *tmp;
rbtree_right_rotate(root, parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
rb_set_black(parent);//旋转前设置好颜色
rb_set_red(gparent);//旋转前设置好颜色
rbtree_left_rotate(root, gparent);
}
}
// 将根节点设为黑色
rb_set_black(root->node);
}
static void rbtree_insert_fixup(RBRoot *root, Node *node)
{
Node* parent;
Node *tmp;
while((parent = rb_parent(node))&&parent->color==RED)
{
Node *gparent=rb_parent(parent);
if(gparent->left==parent)
{
//情形三
Node *uncle=gparent->right;
if(uncle&&rb_is_red(uncle))
{
rb_set_black(parent);
rb_set_black(uncle);
rb_set_red(gparent);
node=gparent;
continue;
}
//情形四
if(parent->right==node)
{
rbtree_left_rotate(root,parent);
tmp=parent;
parent=node;
node=tmp;
}
//情形五
rbtree_right_rotate(root,gparent);
rb_set_black(parent);
rb_set_red(gparent);
}else
{
//情形三
Node *uncle=gparent->left;
if(uncle&&rb_is_red(uncle))
{
rb_set_black(parent);
rb_set_black(uncle);
rb_set_red(gparent);
node=gparent;
continue;
}
//情形四
if(parent->left==node)
{
rbtree_right_rotate(root,parent);
tmp=parent;
parent=node;
node=tmp;
}
//情形五
rbtree_left_rotate(root,gparent);
rb_set_black(parent);
rb_set_red(gparent);
}
}
rb_set_black(root->node);
}
/*
* 添加节点:将节点(node)插入到红黑树中
*
* 参数说明:
* root 红黑树的根
* node 插入的结点 // 对应《算法导论》中的z
*/
static void rbtree_insert(RBRoot *root, Node *node)
{
Node *y = NULL;
Node *x = root->node;
// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
while (x != NULL)
{
y = x;
if (node->key < x->key)
x = x->left;
else
x = x->right;
}
rb_parent(node) = y;//找到父节点并把要插入节点的父节点的指针修改
//修改父节点的子节点指针
if (y != NULL)
{
if (node->key < y->key)
y->left = node; // 情况2:若“node所包含的值” < “y所包含的值”,则将node设为“y的左孩子”
else
y->right = node; // 情况3:(“node所包含的值” >= “y所包含的值”)将node设为“y的右孩子”
}
else
{
root->node = node; // 情况1:若y是空节点,则将node设为根
}
// 2. 设置节点的颜色为红色
node->color = RED;
// 3. 将它重新修正为一颗rb树
rbtree_insert_fixup(root, node);
}
/*
* 创建结点
*
* 参数说明:
* key 是键值。
* parent 是父结点。
* left 是左孩子。
* right 是右孩子。
*/
static Node* create_rbtree_node(Type key, Node *parent, Node *left, Node* right)
{
Node* p;
if ((p = (Node *)malloc(sizeof(Node))) == NULL)
return NULL;
p->key = key;
p->left = left;
p->right = right;
p->parent = parent;
p->color = BLACK; // 默认为黑色
return p;
}
/*
* 新建结点(节点键值为key),并将其插入到红黑树中
*
* 参数说明:
* root 红黑树的根
* key 插入结点的键值
* 返回值:
* 0,插入成功
* -1,插入失败
*/
int insert_rbtree(RBRoot *root, Type key)
{
Node *node; // 新建结点
// 不允许插入相同键值的节点。
// (若想允许插入相同键值的节点,注释掉下面两句话即可!)
if (search(root->node, key) != NULL)
return -1;
// 如果新建结点失败,则返回。
if ((node=create_rbtree_node(key, NULL, NULL, NULL)) == NULL)
return -1;
rbtree_insert(root, node);
return 0;
}
/*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* root 红黑树的根
* node 待修正的节点
*/
static void rbtree_delete_fixup(RBRoot *root, Node *node, Node *parent)
{
Node *other;
//下面的x说的是node
while ((!node || rb_is_black(node)) && node != root->node)
{
if (parent->left == node)
{
//删除
other = parent->right;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的,删除77
rb_set_black(other);
rb_set_red(parent);
rbtree_left_rotate(root, parent);
other = parent->right;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除65时,删除82时,二级进入循环
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->right || rb_is_black(other->right))
{
// Case 3: x的兄弟w是黑色的,并且w的右孩子为黑色。
rb_set_black(other->left);
rb_set_red(other);
rbtree_right_rotate(root, other);
other = parent->right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->right);
rbtree_left_rotate(root, parent);
node = root->node;
break;
}
}
else
{//删除
other = parent->left;
if (rb_is_red(other))
{
// Case 1: x的兄弟w是红色的
rb_set_black(other);
rb_set_red(parent);
rbtree_right_rotate(root, parent);
other = parent->left;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right)))
{
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的,删除77
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else
{
if (!other->left || rb_is_black(other->left))
{
//删除99时,应该是w的左孩子是黑色
// Case 3: x的兄弟w是黑色的,并且w的左孩子是为黑色。
rb_set_black(other->right);
rb_set_red(other);
rbtree_left_rotate(root, other);
other = parent->left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->left);
rbtree_right_rotate(root, parent);
node = root->node;
break;
}
}
}
if (node)
rb_set_black(node);
}
/*
* 删除结点
*
* 参数说明:
* tree 红黑树的根结点
* node 删除的结点
*/
void rbtree_delete(RBRoot *root, Node *node)
{
Node *child, *parent;
int color;
// 被删除节点的"左右孩子都不为空"的情况。
if ( (node->left!=NULL) && (node->right!=NULL) )
{
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
Node *replace = node;
// 获取后继节点,右分支最左的结点就是我们要找的
replace = replace->right;
while (replace->left != NULL)
replace = replace->left;
// "node节点"不是根节点(只有根节点不存在父节点),开始替换
if (rb_parent(node))
{
if (rb_parent(node)->left == node)
rb_parent(node)->left = replace;
else
rb_parent(node)->right = replace;
}
else
// "node节点"是根节点,更新根节点。删除60在这里
root->node = replace;
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace->right;
parent = rb_parent(replace);
// 保存"取代节点"的颜色
color = rb_color(replace);
// "被删除节点"是"它的后继节点的父节点"
if (parent == node)
{
parent = replace;
}
else
{
// child不为空
if (child)
rb_set_parent(child, parent);
//因为结点要移到删除位,所以它的右节点,变为其父亲的左结点
parent->left = child;
replace->right = node->right;
rb_set_parent(node->right, replace);
}
replace->parent = node->parent;
replace->color = node->color;
replace->left = node->left;
node->left->parent = replace;
//移除一个红色结点不需要调整,但是移除一个黑色结点,红黑树平衡就会打破
if (color == BLACK)
rbtree_delete_fixup(root, child, parent);
free(node);
return ;
}
//删除结点有一边是NULL
if (node->left !=NULL)
child = node->left;
else
child = node->right;
//获取删除结点的父亲
parent = node->parent;
// 保存"取代节点"的颜色
color = node->color;
if (child)
child->parent = parent;
// "node节点"不是根节点
if (parent)
{
//在父亲的左边,就把自己孩子放左边,在右边,就把自己孩子放右边
if (parent->left == node)
parent->left = child;
else
parent->right = child;
}
else
root->node = child;//如果是根,孩子就变为根
if (color == BLACK)
rbtree_delete_fixup(root, child, parent);
free(node);
}
/*
* 删除键值为key的结点
*
* 参数说明:
* tree 红黑树的根结点
* key 键值
*/
void delete_rbtree(RBRoot *root, Type key)
{
Node *z, *node;
if ((z = search(root->node, key)) != NULL)
rbtree_delete(root, z);
}
/*
* 销毁红黑树
*/
static void rbtree_destroy(RBTree tree)
{
if (tree==NULL)
return ;
if (tree->left != NULL)
rbtree_destroy(tree->left);
if (tree->right != NULL)
rbtree_destroy(tree->right);
free(tree);
}
void destroy_rbtree(RBRoot *root)
{
if (root != NULL)
rbtree_destroy(root->node);
free(root);
}
/*
* 打印"红黑树"
*
* tree -- 红黑树的节点
* key -- 节点的键值
* direction -- 0,表示该节点是根节点;
* -1,表示该节点是它的父结点的左孩子;
* 1,表示该节点是它的父结点的右孩子。
*/
static void rbtree_print(RBTree tree, Type key, int direction)
{
if(tree != NULL)
{
if(direction==0) // tree是根节点
printf("%2d(B) is root\n", tree->key);
else // tree是分支节点
printf("%2d(%s) is %2d's %6s child\n", tree->key, rb_is_red(tree)?"R":"B", key, direction==1?"right" : "left");
rbtree_print(tree->left, tree->key, -1);
rbtree_print(tree->right,tree->key, 1);
}
}
void print_rbtree(RBRoot *root)
{
if (root!=NULL && root->node!=NULL)
rbtree_print(root->node, root->node->key, 0);
}
/**
* C语言实现的红黑树(Red Black Tree)
*
* @author skywang
* @date 2013/11/18
*/
#define CHECK_INSERT 1 // "插入"动作的检测开关(0,关闭;1,打开)
#define CHECK_DELETE 1 // "删除"动作的检测开关(0,关闭;1,打开)
#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )
void main()
{
int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80,65};
//int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80,65,66,45,77,99,82,23,55,88,33,47};
int i, ilen=LENGTH(a);
RBRoot *root=NULL;
root = create_rbtree();//给指针申请对应的结构体空间
printf("== 原始数据: ");
for(i=0; i<ilen; i++)
printf("%d ", a[i]);
printf("\n");
for(i=0; i<ilen; i++)
{
insert_rbtree(root, a[i]);
#if CHECK_INSERT
printf("== 添加节点: %d\n", a[i]);
printf("== 树的详细信息: \n");
print_rbtree(root);
printf("\n");
#endif
}
printf("== 前序遍历: ");
preorder_rbtree(root);
printf("\n== 中序遍历: ");
inorder_rbtree(root);
printf("\n== 后序遍历: ");
postorder_rbtree(root);
printf("\n");
if (rbtree_minimum(root, &i)==0)
printf("== 最小值: %d\n", i);
if (rbtree_maximum(root, &i)==0)
printf("== 最大值: %d\n", i);
printf("== 树的详细信息: \n");
print_rbtree(root);
printf("\n");
#if CHECK_DELETE
for(i=0; i<ilen; i++)
{
printf("== 删除节点: %d\n", a[i]);
delete_rbtree(root, a[i]);
if (root)
{
printf("== 树的详细信息: \n");
print_rbtree(root);
printf("\n");
}
}
#endif
destroy_rbtree(root);
}