目录
前言
1.双关节机械手臂模型
2.神经网络自适应律设计
3. 滑模控制律设计
4. 仿真分析
4.1 仿真模型
4.2 仿真结果
4.3 小结
5 学习问题
前言
上一篇文章我介绍了神经网络补偿的机理,只不过控制律不同,本章我们结合滑模理论设计控制律,所以本质还是:神经网络逼近扰动+控制律。
基于神经网络(RBF)补偿的双关节机械手臂自适应控制_Mr. 邹的博客-CSDN博客
其实在我之前的文章中早就已经用到过这种补偿+控制的思想,只不过用的不是神经网络补偿,而是基于模糊推理机的方法进行补偿,详情请见:
VSC/SMC(十五)——基于模糊逼近的积分滑模控制_Mr. 邹的博客-CSDN博客
基于模糊逼近系统不确项的滑模自适应控制_模糊基向量_Mr. 邹的博客-CSDN博客
一类综合的模糊化自适应滑模控制_模糊自适应滑模控制_Mr. 邹的博客-CSDN博客
1.双关节机械手臂模型
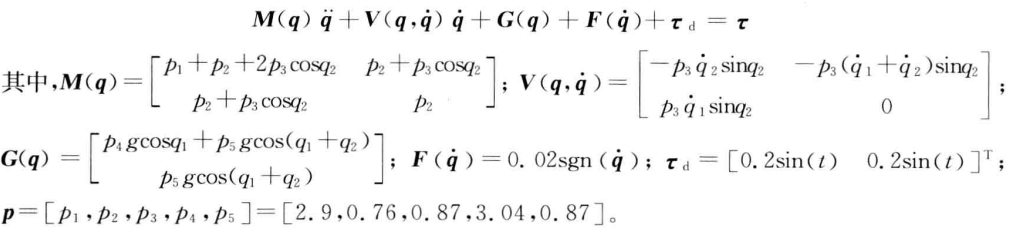
2.神经网络自适应律设计
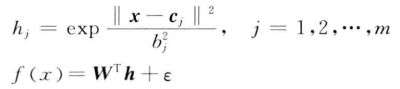
这里不再赘述了,上一篇文章介绍了:
基于神经网络(RBF)补偿的双关节机械手臂自适应控制_Mr. 邹的博客-CSDN博客
所设计的自适应律为:
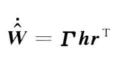
3. 滑模控制律设计
滑模面选取:
r=e'+k*e
控制律设计为:
τ = f^+Kv*r-v
其中v为滑模鲁棒项。
注:
①由于系统是2自由度的,即有两个位置指令,所以e和de也是2维的,所以滑模面系数k也是2维的;即相当于分别为2位置设计了2滑模面。
4. 仿真分析
4.1 仿真模型
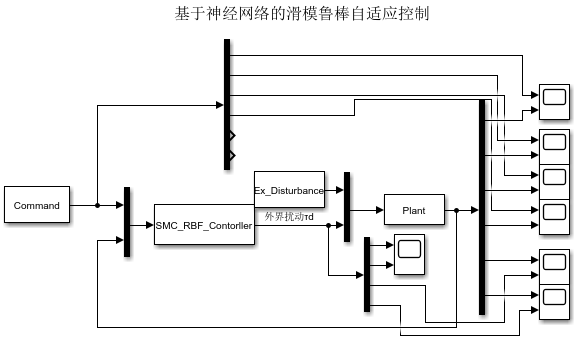
4.2 仿真结果
调节参数选取:Kv=[50 0;0 50],k = [5 0;0 5]
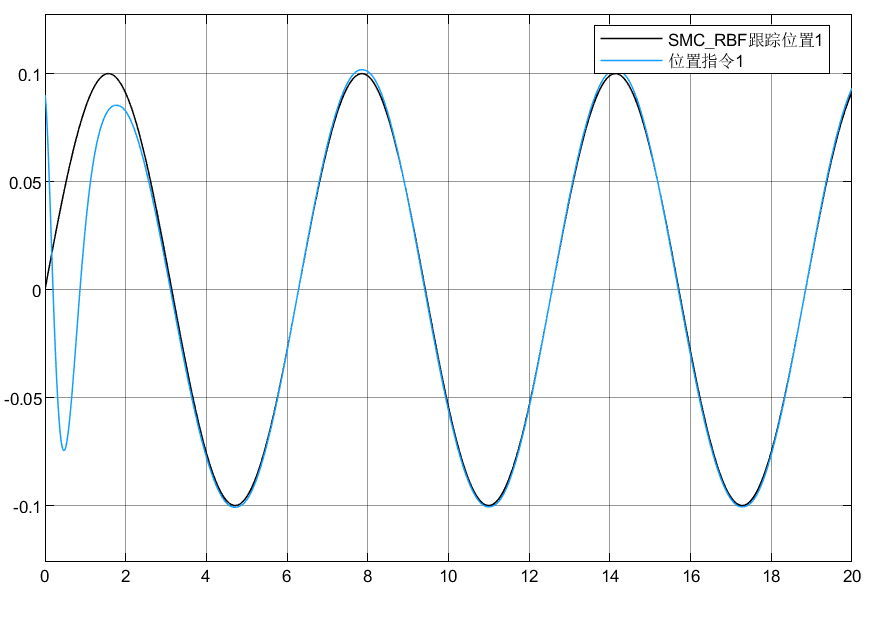
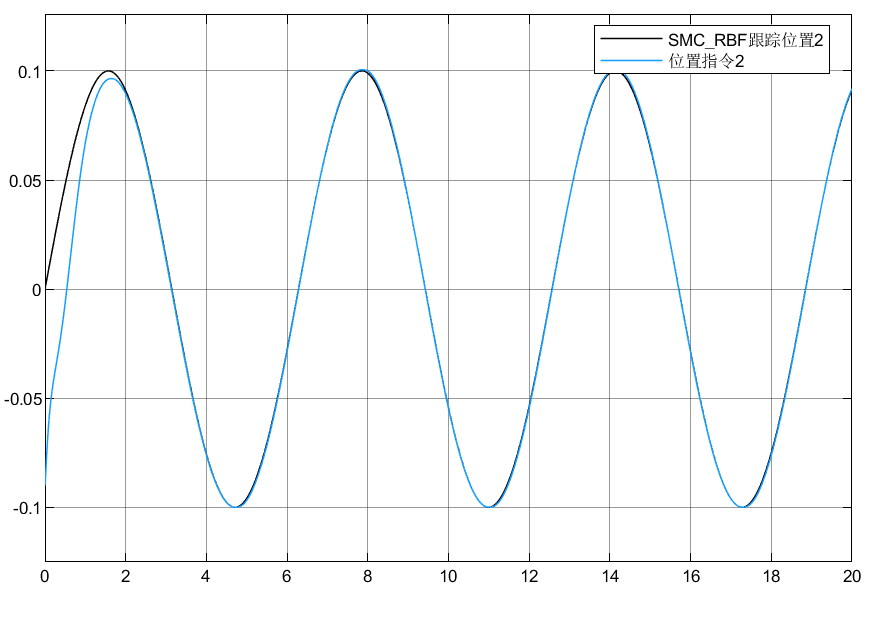
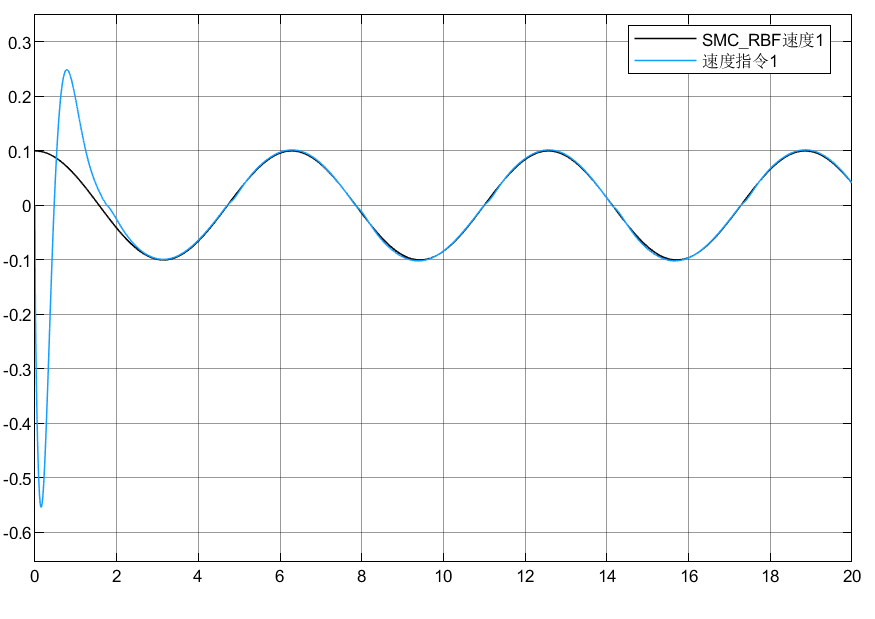
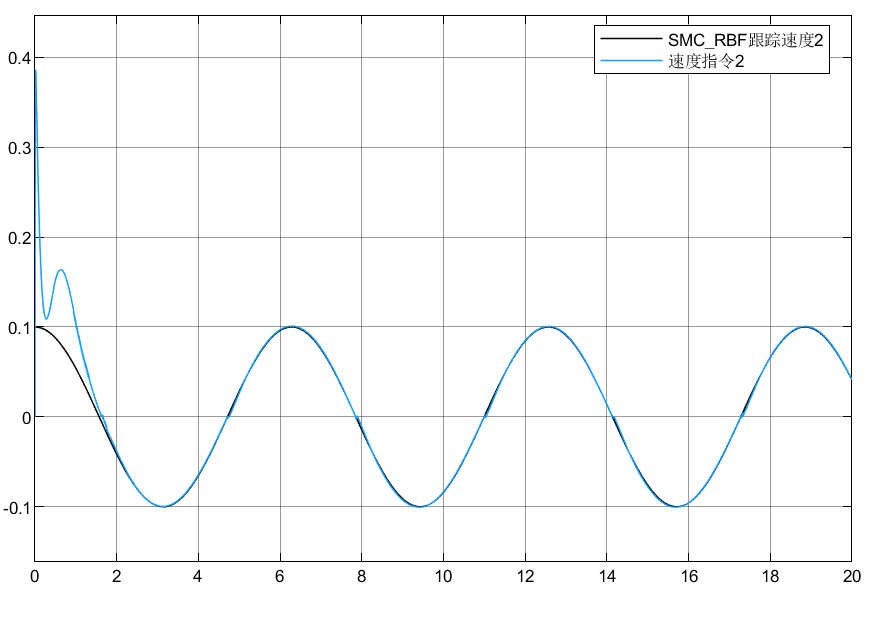
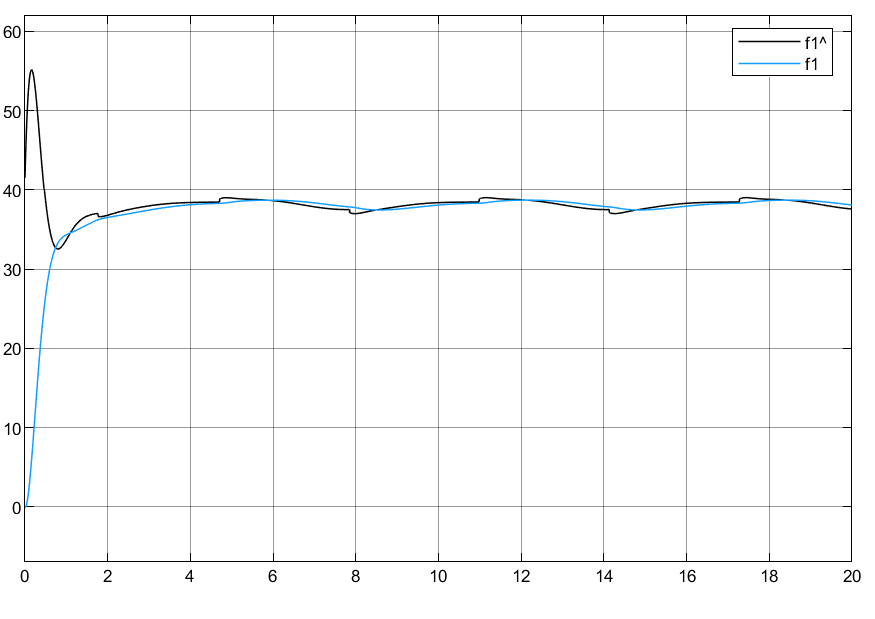
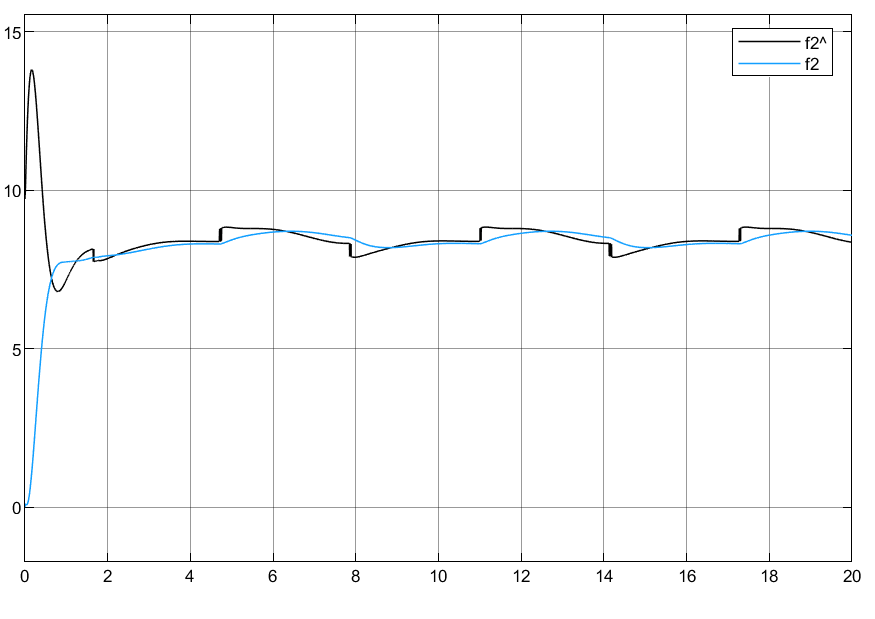
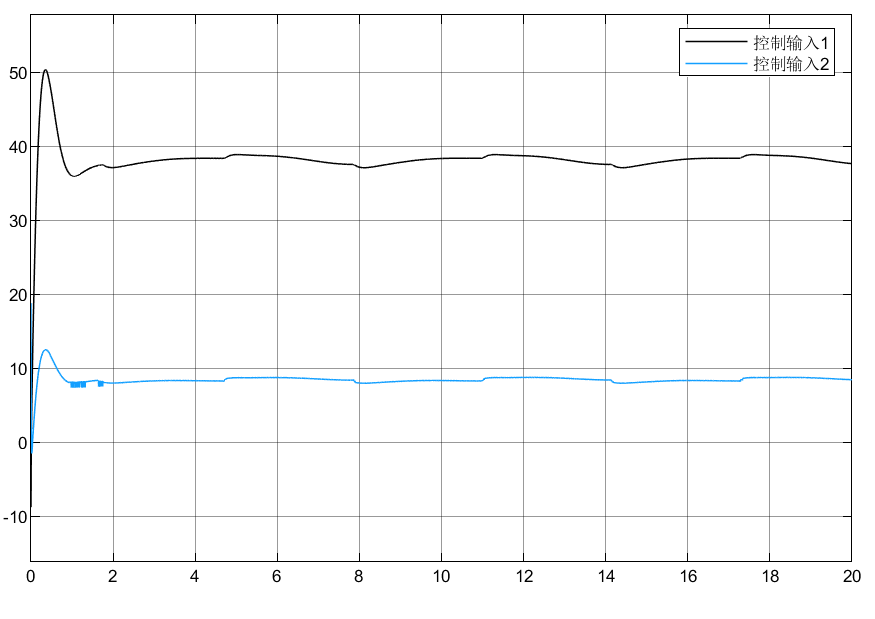
4.3 小结
可以看到模型即使存在不确定,外界扰动情况下,也能跟踪目标指令,虽然估计的扰动没有做到很精准,但是结合滑模的鲁棒性,能够保证系统在扰动下跟踪目标。
5 学习问题
①自适应律是参考文献来的,为何用等效滑模思想推导有些对不上;
②对于误差是指令-实际,需要统一好,并且关于推导控制输入以及稳定性证明分析。