文章目录
- 对称锥规划:锥与对称锥
- 锥的几何形状
- 常用的指向锥
- Nonnegative Orthant
- 二阶锥
- 半定锥
- 对称锥
- 对称锥的平方操作
- 对称锥的谱分解
- 对称锥的自身对偶性
- 二阶锥规划SOCP
- 参考文献
对称锥规划:锥与对称锥
本文主要讲锥与对称锥的一些基本概念。
基础预备:
凸优化学习笔记(一)


锥的几何形状
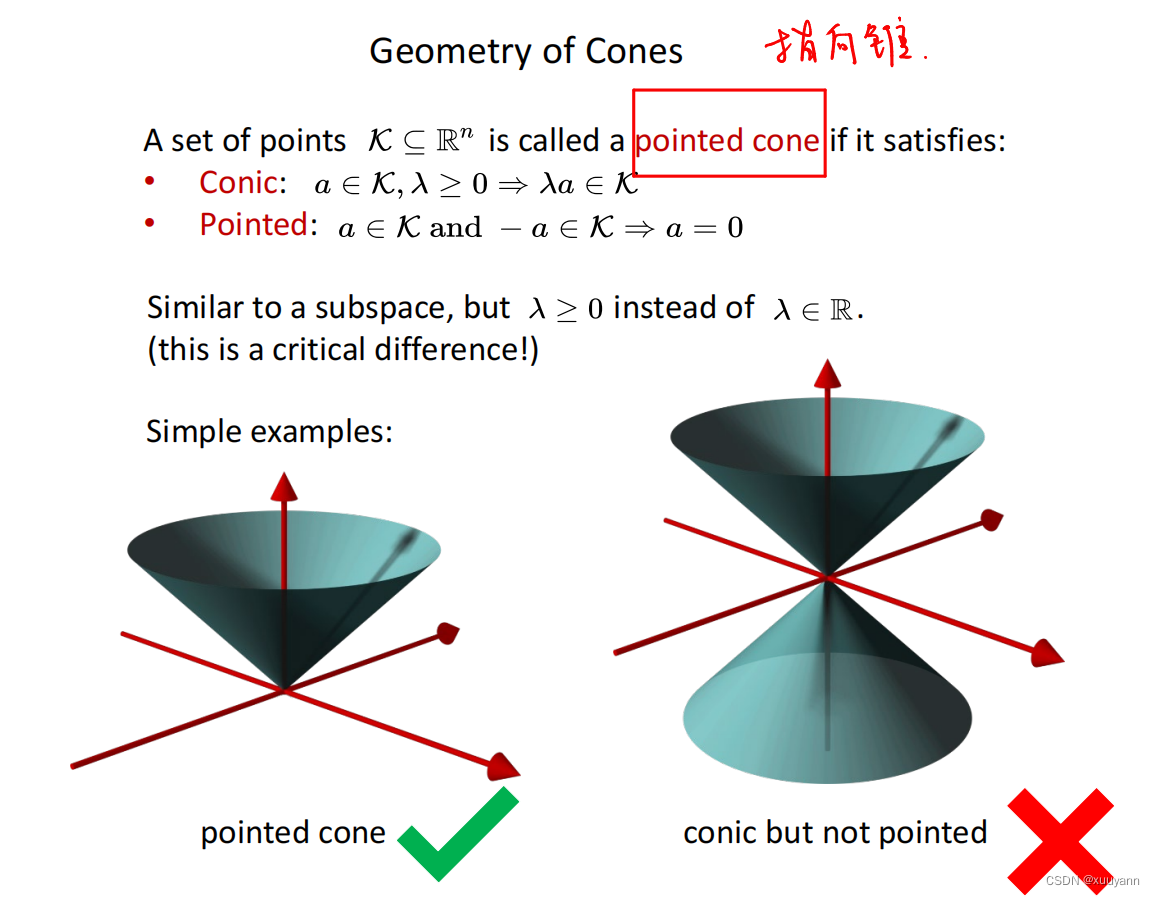
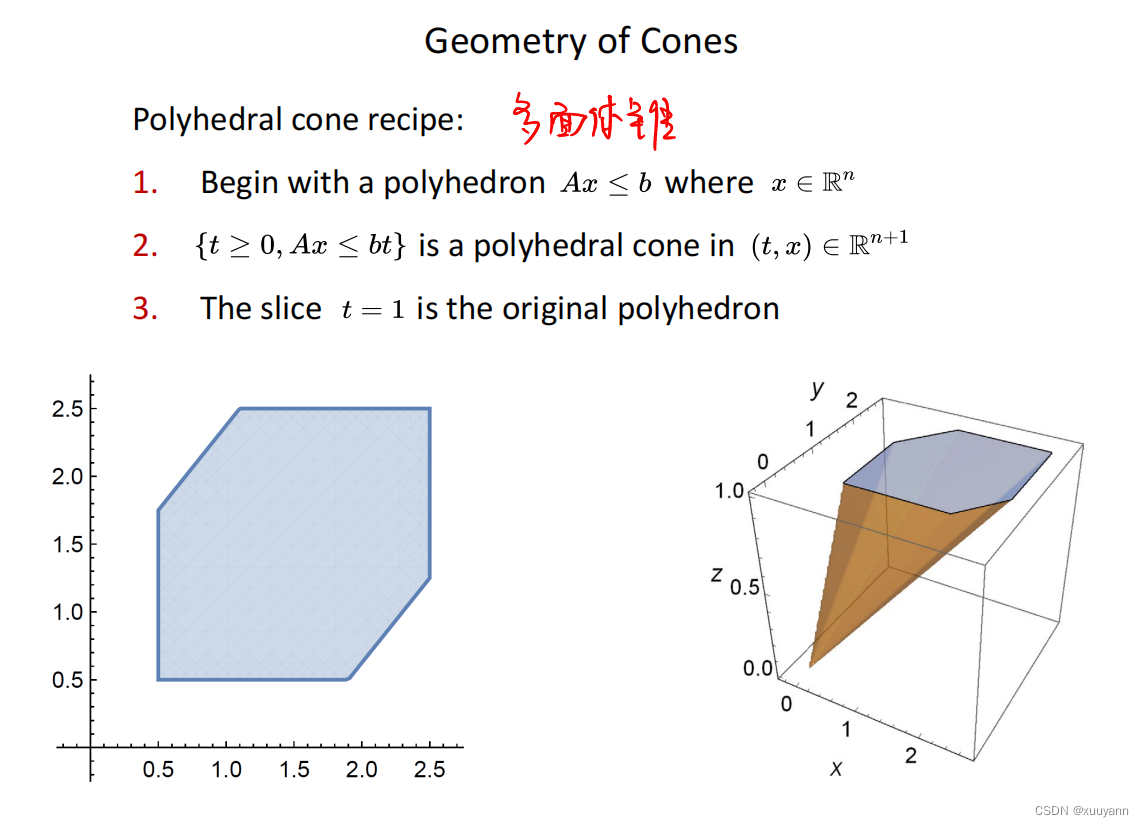
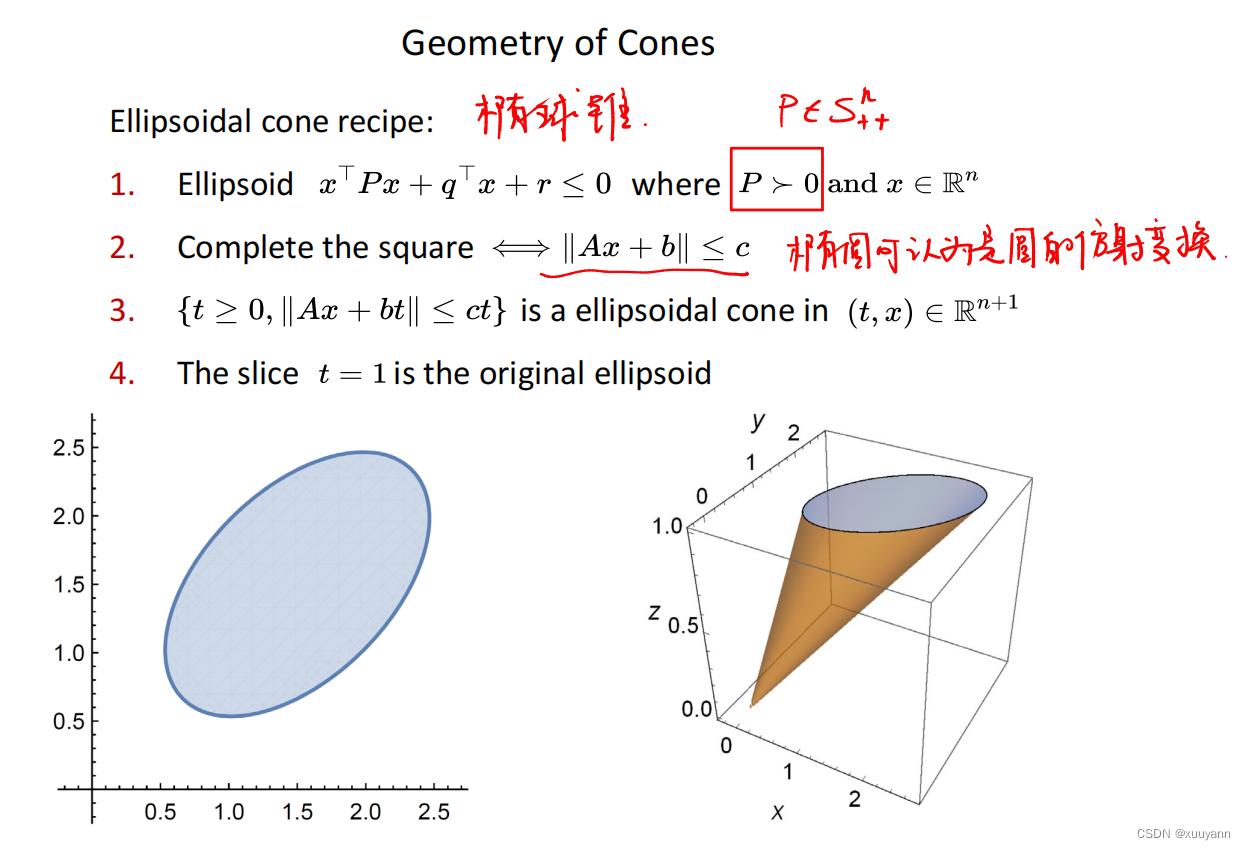
常用的指向锥

Nonnegative Orthant
当n=2时,可以理解为非负的象限,当n=3时,可以理解为非负的卦限。经过仿射变换后,可以理解为n个半空间的交。
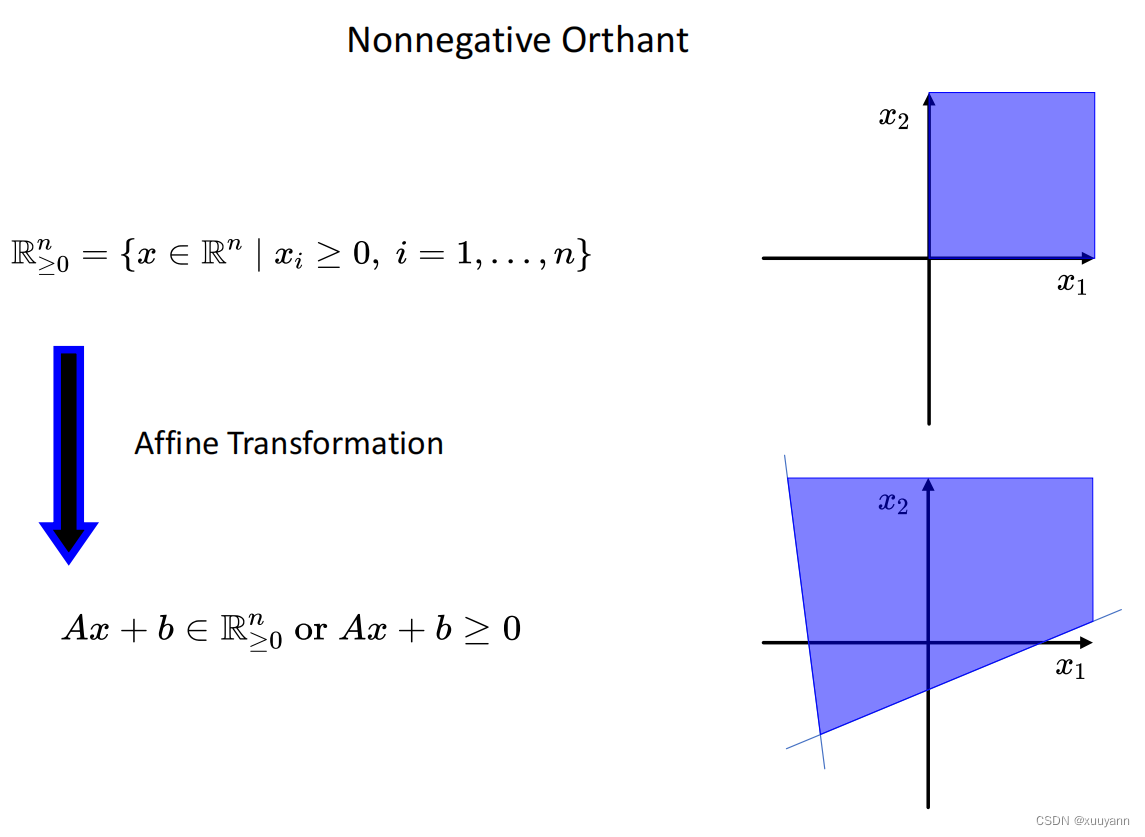
二阶锥
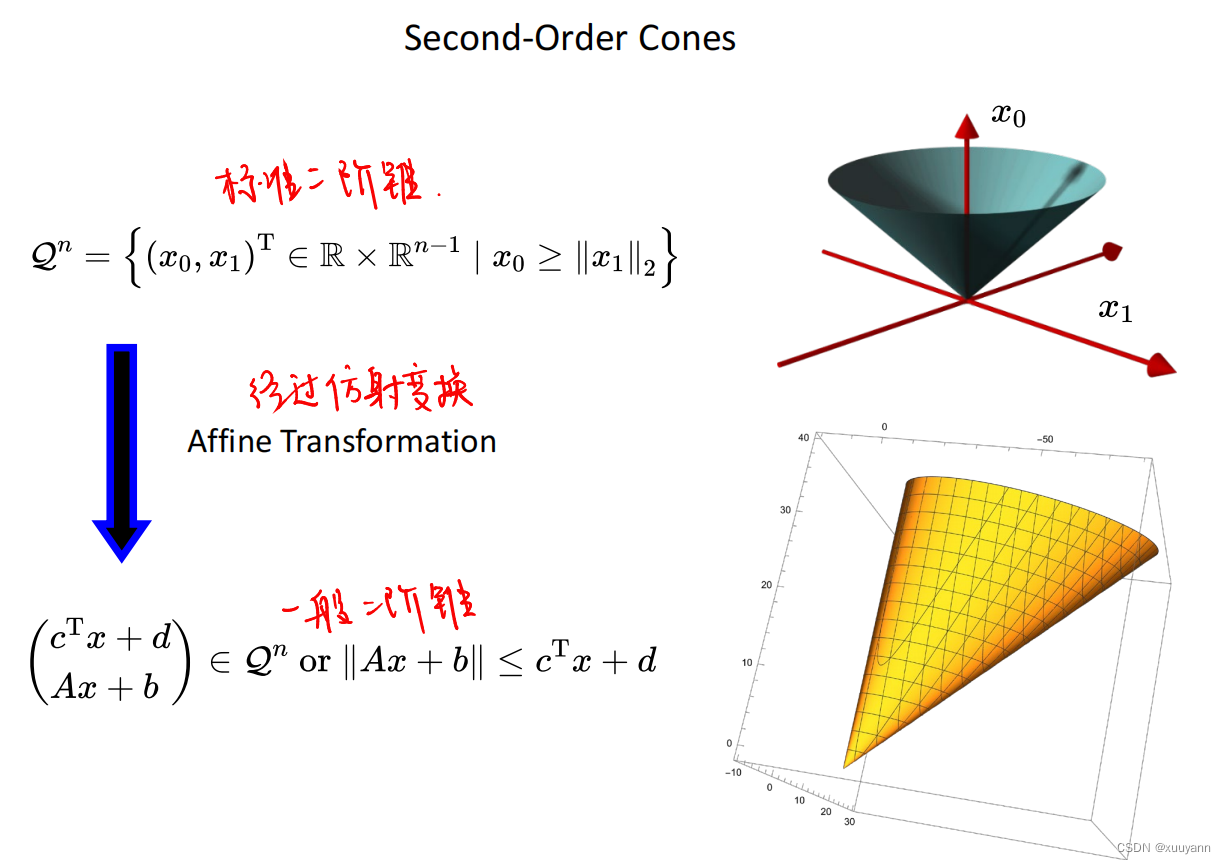
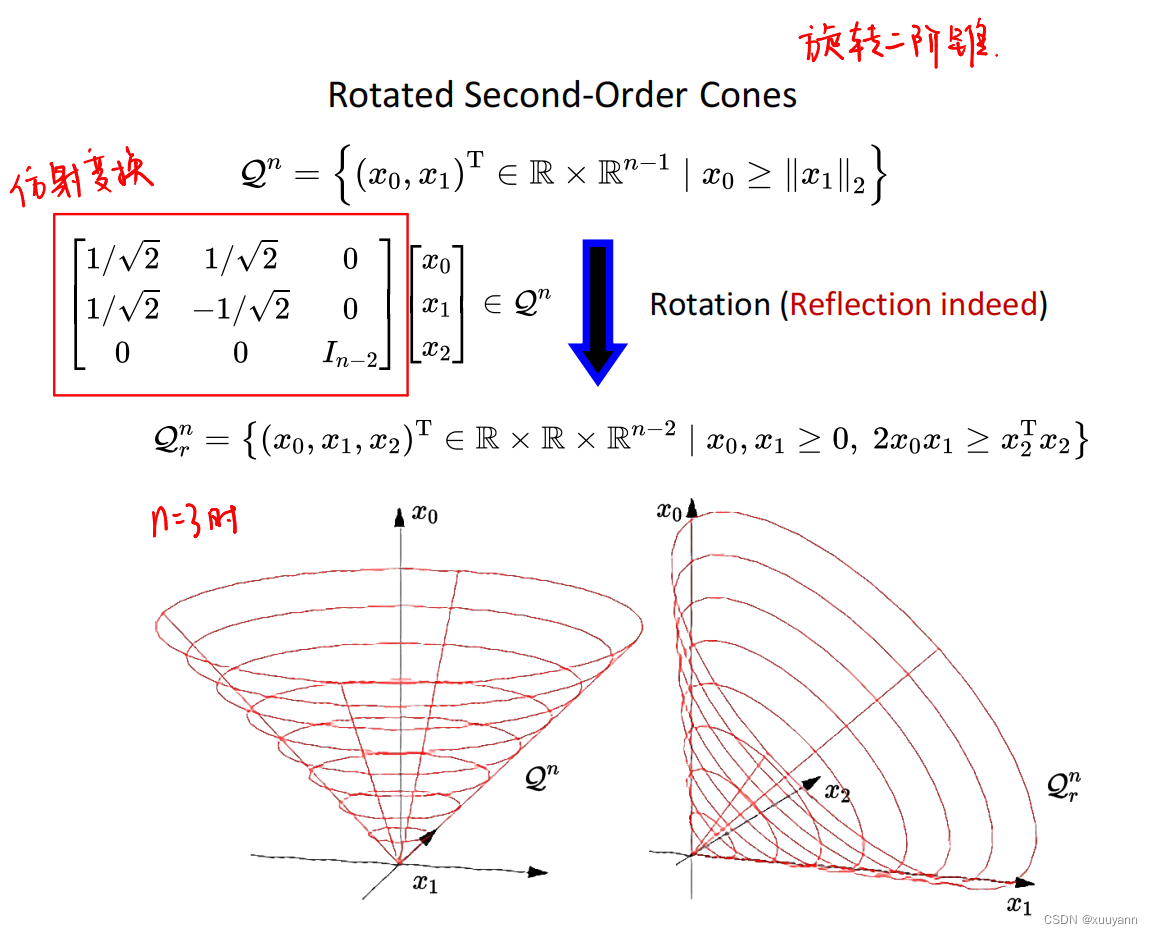
半定锥
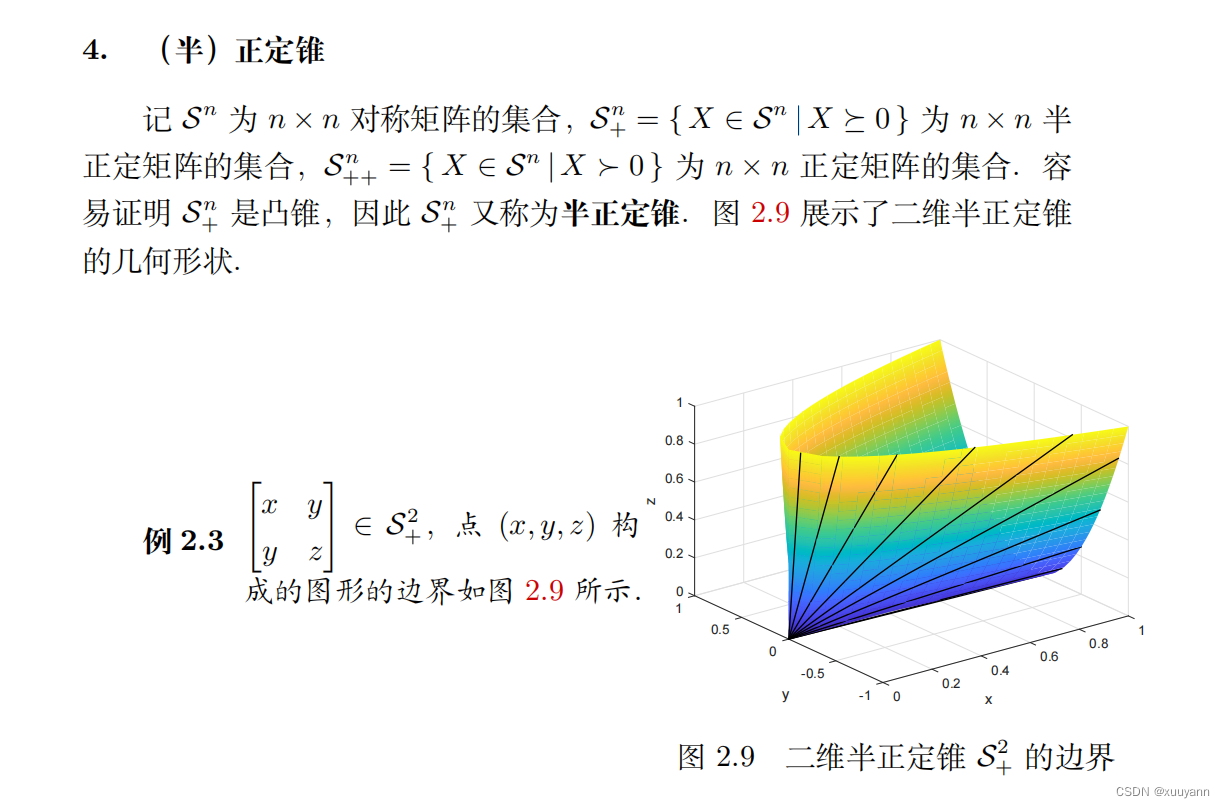

对称锥

对称锥的平方操作
通过欧几里得若当代数 ( R n , ∘ ) \left(\mathbb{R}^n, \circ\right) (Rn,∘),可以将对称锥写成一个平方的形式,便于规划分析与统一表达。


对称锥的谱分解

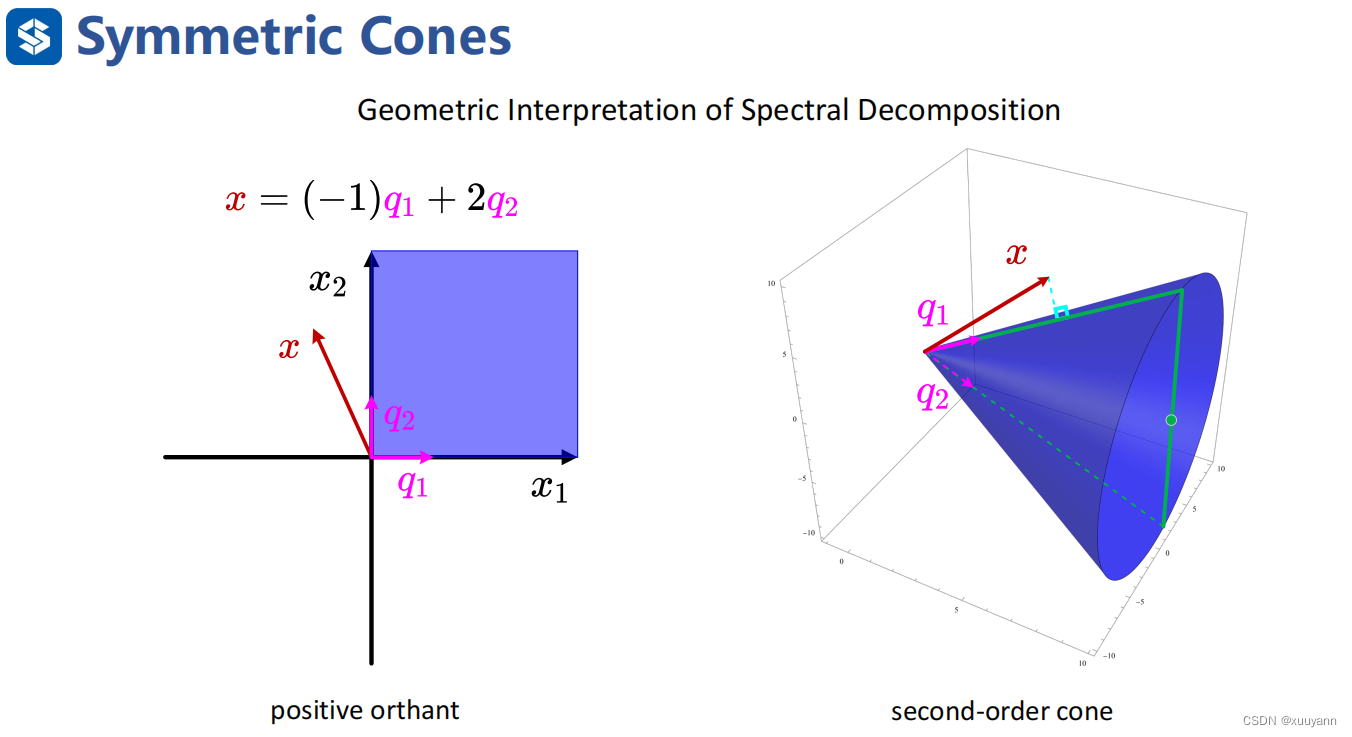

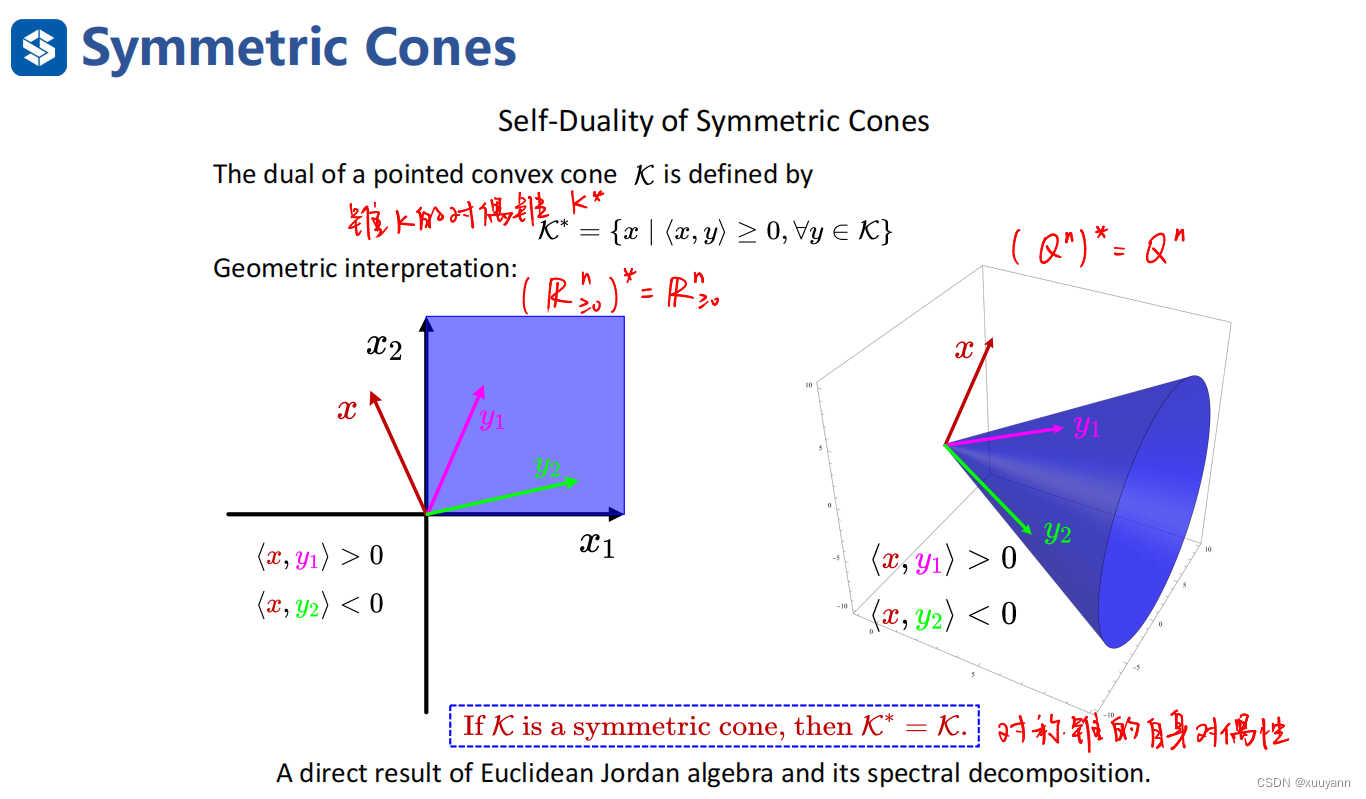
对称锥的自身对偶性
对称锥的对偶锥还是它本身。
二阶锥规划SOCP
很多问题都可以转化为二阶锥规划来求解,而二阶锥规划能够使用内点法很快求解。例如下图,使用松弛方式可以将QP问题转化成SOCP问题。

根据Shur补定理,又可将SOCP问题转化为SDP问题。因此,就问题的表达能力而言,LP<QP<SOCP<SDP。

参考文献
机器人中的数值优化
最优化:建模、算法与理论/最优化计算方法
正定矩阵的相关性质,凸锥
锥,凸锥,二阶锥,二阶锥规划