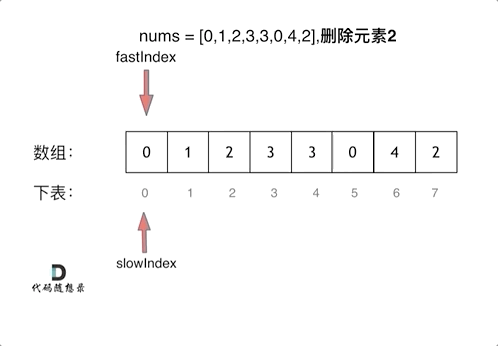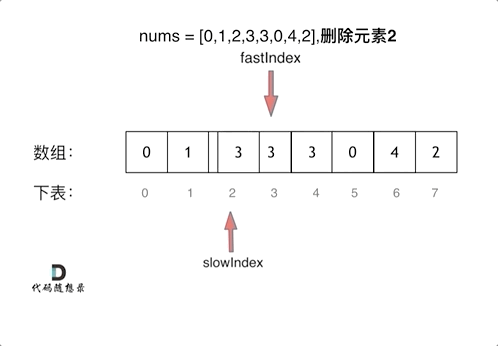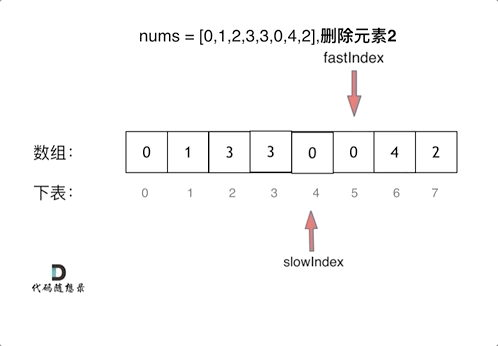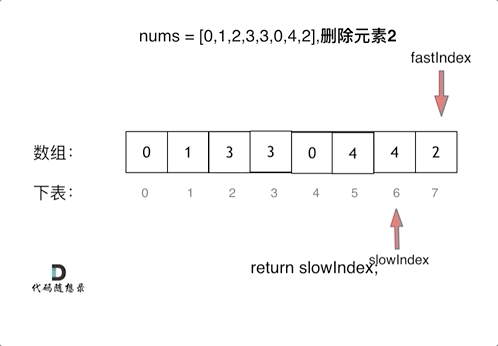
神经网络权重不可为相同的值，比如都为0，因为如果这样网络正向传播输出和反向传播结果对于各权重都完全一样，导致设置多个权重和设一个权重毫无区别。我们需要使用随机数作为网络权重

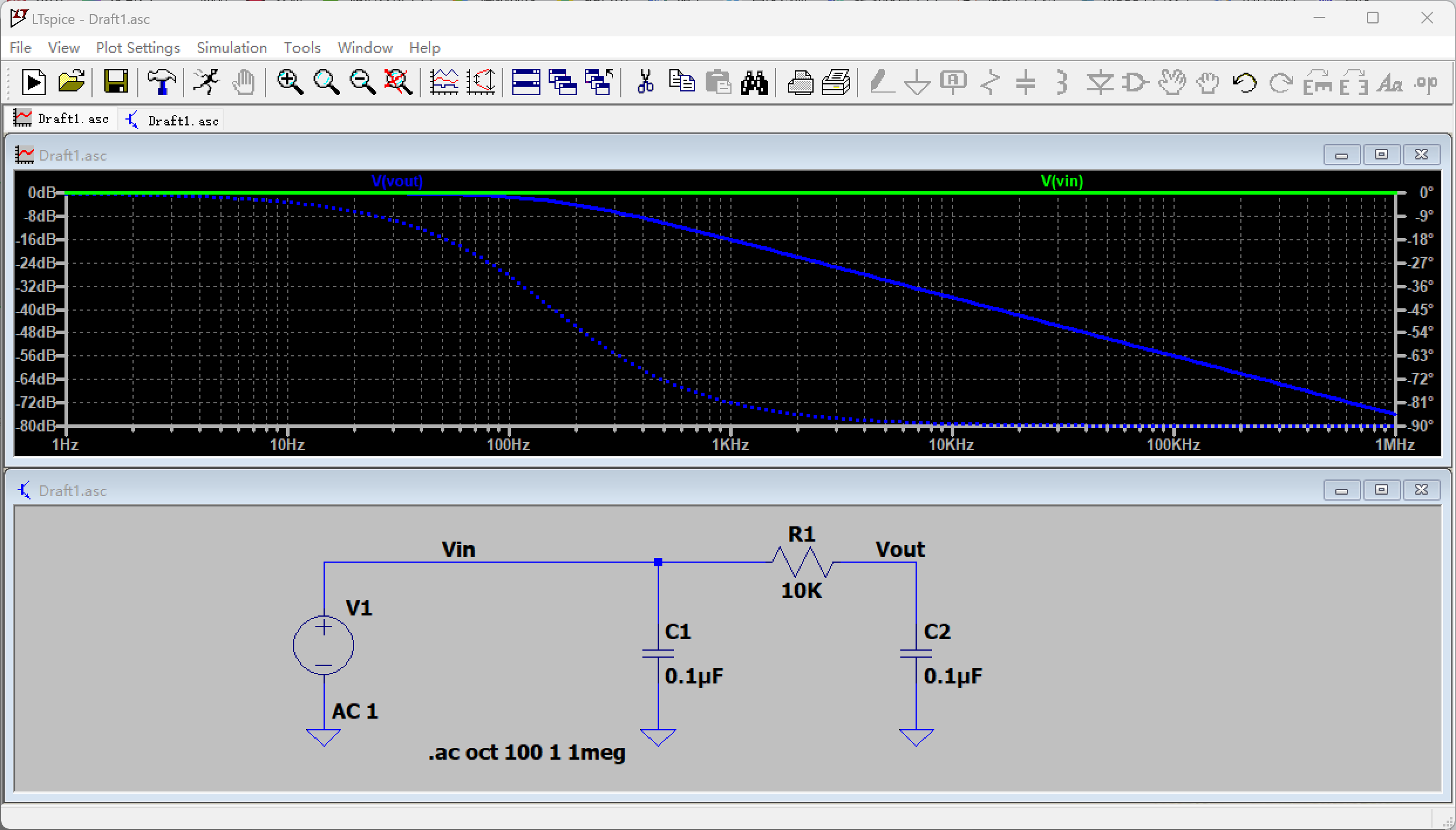
实验程序

在以下实验中，我们使用5层神经网络，每层神经元个数100，使用sigmoid作为激活函数，向网络传入1000个正态分布随机数，测试使用不同的随机数对网络权重的影响。

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def ReLU(x):
    return np.maximum(0, x)


def tanh(x):
    return np.tanh(x)
    
input_data = np.random.randn(1000, 100)  # 1000个数据
node_num = 100  # 各隐藏层的节点（神经元）数
hidden_layer_size = 5  # 隐藏层有5层
activations = {}  # 激活值的结果保存在这里

x = input_data

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    # 改变初始值进行实验！
    w = np.random.randn(node_num, node_num) * 1
    # w = np.random.randn(node_num, node_num) * 0.01
    # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num)
    # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num)


    a = np.dot(x, w)


    # 将激活函数的种类也改变，来进行实验！
    z = sigmoid(a)
    # z = ReLU(a)
    # z = tanh(a)

    activations[i] = z

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    if i != 0: plt.yticks([], [])
    # plt.xlim(0.1, 1)
    # plt.ylim(0, 7000)
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

1 标准差为1随机正态

在这一情况下，权重值主要集中于0和1.由于sigmoid在接近0和1时导数趋于0，这一数据分别会导致反向传播中梯度逐渐减小，这一现象称为梯度消失

2 标准差为0.01随机正态

这时神经网络权重集中在0.5附近，此时不会出现梯度消失，但是由于值集中在同一区间，多个神经网络会输出几乎相同的值，使得神经网络表现能力受限（如开头所说）

3 使用Xavier初始值

Xavier初始值为保证各层权重值具有足够广度设计。其推导出的最优初始值为每一层初始权重值是1/√N，其中N为上一层权重个数

使用sigmoid激活函数和Xavier初始值结果：

可以看到此时权重初始值的值域明显大于了之前的取值。Xavier初始值是基于激活函数为线性函数的假设推导出的。sigmoid函数关于（0， 0.5）对称，其在原点附近还不是完美的线性。而tanh函数关于原点对称，在原点附近可以基本近似于直线，其使用Xavier应该会产生更理想的参数值

使用tanh激活函数和Xavier初始值：

ReLU函数的权重设置

ReLU函数有自己独特的默认权重设置，称为He初始值，其公式为2/√N标准差的随机数，N为上一次神经元个数。

在该分布中，各层广度分布基本相同，这使得即使层数加深，也不容易出现梯度消失问题

使用mnist数据集对不同初始化权重方法进行测试：

该程序使用0.01随机正态，Xavier + sigmoid，He + ReLU进行2000轮反向传播，并绘制总损失关于迭代次数图象

# coding: utf-8
import os
import sys

sys.path.append("D:\AI learning source code")  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000


# 1:进行实验的设置==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)

networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
    networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
                                  output_size=10, weight_init_std=weight_type)
    train_loss[key] = []


# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    for key in weight_init_types.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizer.update(networks[key].params, grads)
    
        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)
    
    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in weight_init_types.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))


# 3.绘制图形==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()

在该图象中可以看到，0.01随机正态由于梯度丢失问题，权重更新速率极慢，在2000次迭代中总损失基本没有变化。Xavier和He都正常进行了反向传播得到了更准确的网络参数，其中He似乎学习速率更快一些