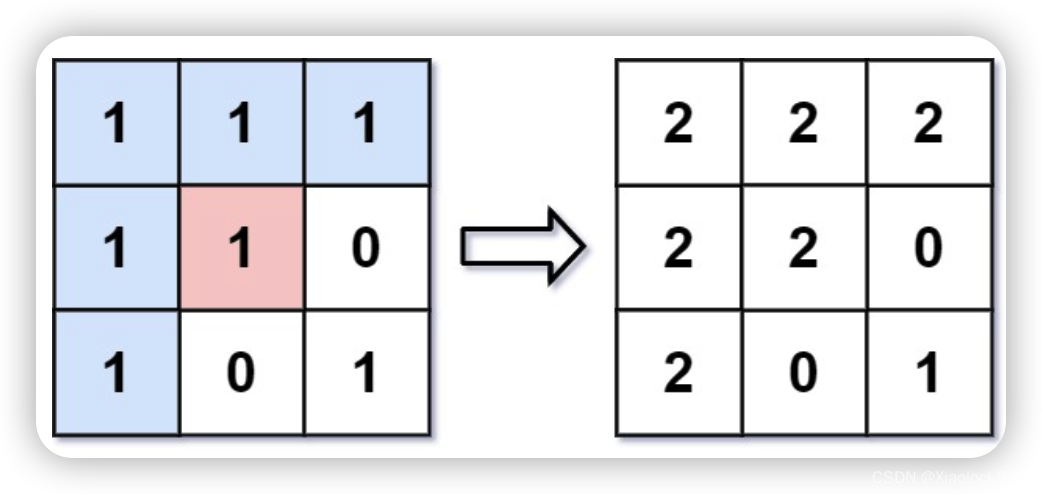
假设给定混乱数据为:3,0,1,3,6,5,4,2,1,9。
下面我们将通过使用计数排序的思想来完成对上面数据的排序。(先不谈负数)
计数排序
该排序的思路和它的名字一样,通过记录数据出现的次数,来完成数据的排序。我们默认实现的是升序。
思路:
1. 首先我们要先记录下数据的出现次数
这个很简单,我们只需要遍历一遍原数组即可(注意看代码后面的注释!),如下:
count是我们用来记录次数的新数组
for (int i = 0; i < sz; ++i)
{
count[a[i]]++;//以原数据的值作为下标!!
}以上面的数据为例,结果如下:
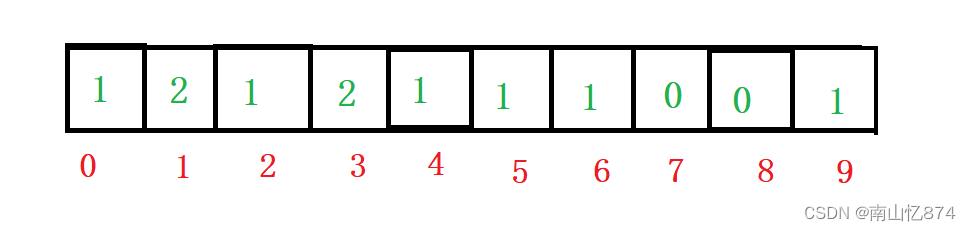
0-9的数字就7和8没有出现。
所以我们现在可以初步的来想一下,用于统计次数的count数组大小是否可以直接使用原数据中最大的一个数据??(之后回答)。
2. 拿到了次数之后,我们就可以开始向原数组进行覆写数据。
比如0出现了1次,我们就将原数组的第1覆写为0。
1出现了2次,将原数组的第二位和第三位覆写为1。
2出现了1次,原数组第四位覆写为2.
.....
7出现了0次,不进行覆写,跳到下一个数据。
8出现了0次,不进行覆写,跳到下一个数据。
...
以此类推,当遍历完count数组之后,数据的覆写就完成了,也就完成了排序。
如下所示:
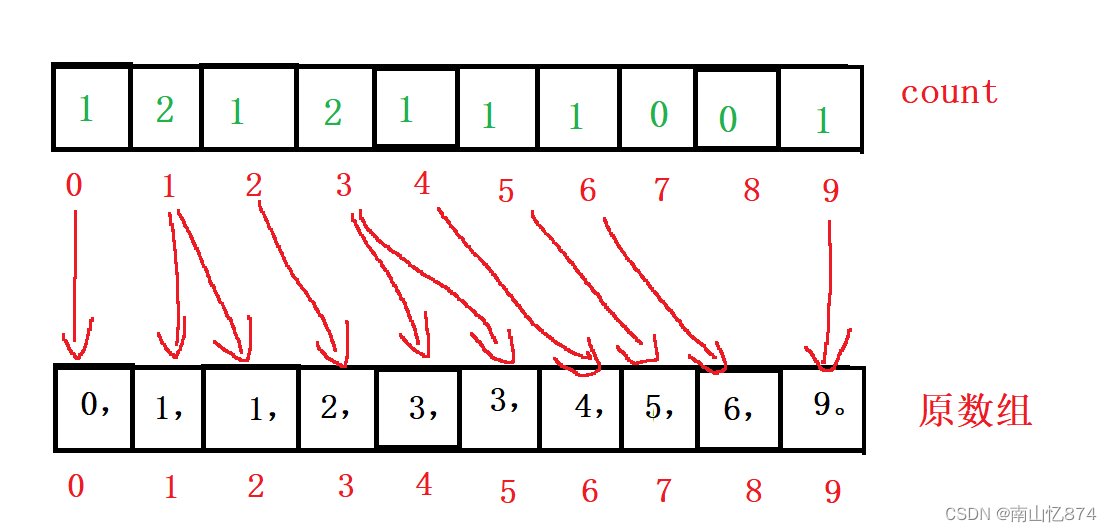
计数排序的思路已经完成了,现在我们来考虑一下细节问题
1.如何确定count数组的大小
对于上面的数据我们确实可以直接使用9作为count数组的最大值,但是假设有这样一组数据
1000,1001,1002,1008,1009,10005。
此时如果我们选用1009作为count数组的最大值,那么0-998个数组空间根本不会被使用。
所以根据原数据的最大值来确定count数组的最大值是不合理的,我们应该使用原数据中的
最大值-最小值+1来当作count数组的最大值
1009-1000 + 1 = 10;
那么我在统计数据的出现次数的时候也就需要减去一个最小值,比如1000-1000=0;
那么1000就成功的被映射在了count数组的下标0位置处.
1009-1000 = 9,1009也就映射在了下标9的位置处
那么我们在根据次数覆写数据的时候,也就需要count的下标再加上原数据的最小值了。
0+1000 = 1000
1+1000 = 1001
2+1000 = 1002
8+1000 = 1008
9+1000 = 1009
至此我们就完全解决了count数组大小的问题和对极端数据可能会造成空间浪费的问题。
这里是完成的源代码:
#include <stdlib.h>
#include <stdio.h>
#include <assert.h>
void Countsort(int* a, int sz)
{
//先找去最大和最小的值,以确定数据范围
int max = a[0], min = a[0];
for (int i = 1; i < sz; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1;//范围
int* count = (int*)calloc(range, sizeof(int));
if (count == NULL)
perror("calloc faild\n");
//先统计出次数
for (int i = 0; i < sz; ++i)
{
count[a[i] - min]++;//减去最小值是为了防止最大值和最小值差距过大导致的空间浪费
}
//覆写原数组--排序过程
int j = 0;
for (int i = 0; i < range; ++i)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
}2.原数据中有负数怎么办?
其实这个问题根本不用回答,我们先来用一组负数的数据跑一下,看结果如何:
int main()
{
int arr[] = { -9,-8,-4,0,3,3,4,2,1,1,8,9,7 };
int sz = sizeof(arr) / sizeof(arr[0]);
Countsort(arr, sz);
for (int i = 0; i < sz; ++i)
{
printf("%d ", arr[i]);
}
return 0;
}运行结果:
![]()
可以看到运行结果完全正确!
至于为什么,就留给大家自己探究了,相信你一定可以!!