704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
解题思路:
还是喜欢左闭右闭的写法。左闭右闭的写法关键是:
- 当l = 0, r = n - 1的时候因为r这个值我们在数组中可以取到,while(l <= r) 是正确写法 主要看能不能取到这个值。
- 二分的最大优势是在于其时间复杂度是O(logn),通常看到有序数组都要第一时间反问自己是否可以使用二分。
- 关于二分mid溢出问题解答:
-
- mid = (l + r) / 2时,如果l + r 大于 INT_MAX(C++内,就是int整型的上限),那么就会产生溢出问题(int类型无法表示该数)
- 所以写成 mid = l + (r - l) / 2或者 mid = l + ((r - l) >> 1) 可以避免溢出问题
C++版本:
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
while(left<=right){
int middle = left + (right-left)/2;
if(nums[middle] < target){
left = middle + 1;
}
else if(nums[middle] > target){
right = middle - 1;
}
else return middle;
}
return -1;
}
};Python版本
class Solution:
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
while(left <= right):
middle = (left + right)//2
if(nums[middle]>target):
right = middle - 1
elif(nums[middle]<target):
left = middle + 1
else:
return middle
return -1 27. 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
输入:nums = [3,2,2,3], val = 3 输出:2, nums = [2,2] 解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
输入:nums = [0,1,2,2,3,0,4,2], val = 2 输出:5, nums = [0,1,4,0,3] 解释:函数应该返回新的长度,并且 nums 中的前五个元素为0,1,3,0,4.
解题思路:
这个题需要不额外使用空间,只能原地修改。
解法1:采用Vector中的erase消除指定值,传入相应的迭代器即可删除,注意erase返回的是指向下一个值的迭代器。
C++版本
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
for(vector<int>::iterator iter = nums.begin(); iter != nums.end();)
if(*iter == val){
iter = nums.erase(iter);
}
else{
iter++;
}
return nums.size();
}
};Python版本:Python则采用List的remove方法
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
while val in nums:
nums.remove(val)
return len(nums)2、采用快慢指针法。
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
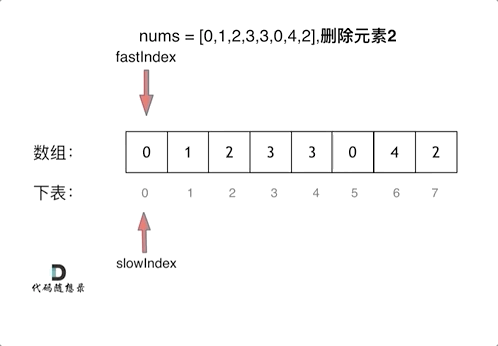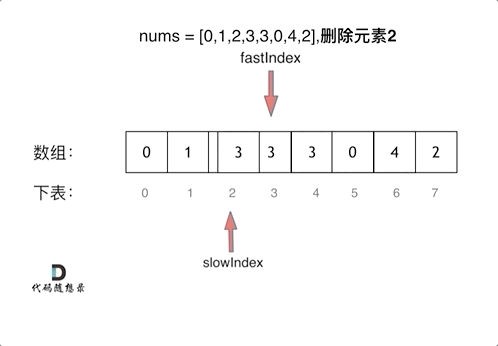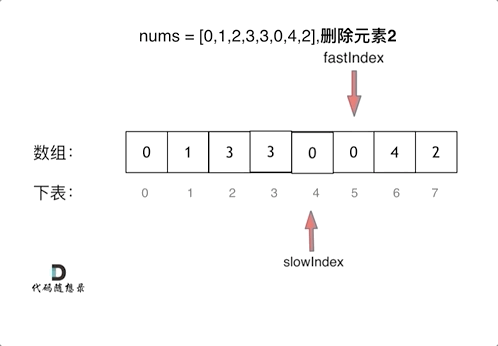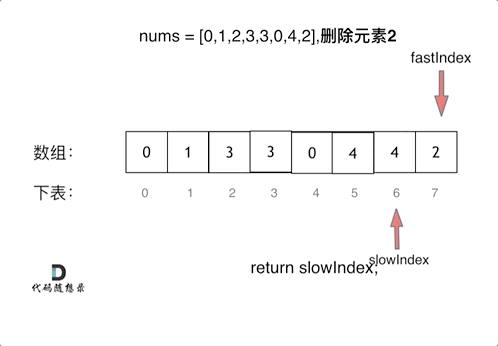
C++版本:
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int fastIndex = 0, slowIdex = 0;
for(fastIndex; fastIndex<nums.size();fastIndex++){
if (nums[fastIndex] == val){
continue;
}
else{
nums[slowIdex] = nums[fastIndex];
slowIdex++;
}
}
return slowIdex;
}
};python版本:
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
slowIndex = 0
for fastIndex in range(len(nums)):
if nums[fastIndex] == val:
continue
else:
nums[slowIndex] = nums[fastIndex]
slowIndex += 1
return slowIndex