目录
1. 冒泡排序法排序 ★
2. 有效的数独 ★★
3. 不同的二叉搜索树 II ★★
附录
二叉搜索树
1. 冒泡排序法排序
输入n(1≤n≤10)个整数,用冒泡排序法对其从小到大排序,共进行n-1趟,要求输出每一趟的排序情况
输入格式:
先输入个数n,再输入n个整数。
输出格式:
第1趟结果
第2趟结果
......
第n-1趟结果
每个数后面有一个空格,每个序列占一行。
输入样例:
5
4 2 3 2 1输出样例:
2 3 2 1 4
2 2 1 3 4
2 1 2 3 4
1 2 2 3 4代码:
#include "stdio.h"
int main()
{
int arr[10];
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%d", &arr[i]);
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
int t = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = t;
}
}
for (int j = 0; j < n; j++)
printf("%d ", arr[j]);
printf("\n");
}
return 0;
}输入输出:
5
4 2 3 2 1
2 3 2 1 4
2 2 1 3 4
2 1 2 3 4
1 2 2 3 4
--------------------------------
Process exited after 12.95 seconds with return value 0
请按任意键继续. . .
2. 有效的数独
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
- 数字
1-9在每一行只能出现一次。 - 数字
1-9在每一列只能出现一次。 - 数字
1-9在每一个以粗实线分隔的3x3宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 '.' 表示。
注意:
- 一个有效的数独(部分已被填充)不一定是可解的。
- 只需要根据以上规则,验证已经填入的数字是否有效即可。
示例 1:

输入:board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:true
示例 2:
输入:board = [["8","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出:false 解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9board[i].length == 9board[i][j]是一位数字或者'.'
代码:
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
bool isValidSudoku(vector<vector<char>> &board)
{
for (int i = 0; i < board.size(); i++)
{
vector<bool> mark(10);
for (int j = 0; j < board.size(); j++)
{
if (!valid(board, mark, i, j))
{
return false;
}
}
}
for (int j = 0; j < board.size(); j++)
{
vector<bool> mark(10);
for (int i = 0; i < board.size(); i++)
{
if (!valid(board, mark, i, j))
{
return false;
}
}
}
for (int k = 0; k < board.size(); k++)
{
int sr = k / 3 * 3;
int sc = (k % 3) * 3;
vector<bool> mark(10);
for (int i = sr; i < sr + 3; i++)
{
for (int j = sc; j < sc + 3; j++)
{
if (!valid(board, mark, i, j))
{
return false;
}
}
}
}
return true;
}
private:
bool valid(vector<vector<char>> &board, vector<bool> &mark, int i, int j)
{
if (board[i][j] != '.')
{
int index = board[i][j] - '0';
if (mark[index])
{
return false;
}
else
{
mark[index] = 1;
}
}
return true;
}
};
int main()
{
Solution s;
vector<vector<char>> board = {
{'5','3','.','.','7','.','.','.','.'},
{'6','.','.','1','9','5','.','.','.'},
{'.','9','8','.','.','.','.','6','.'},
{'8','.','.','.','6','.','.','.','3'},
{'4','.','.','8','.','3','.','.','1'},
{'7','.','.','.','2','.','.','.','6'},
{'.','6','.','.','.','.','2','8','.'},
{'.','.','.','4','1','9','.','.','5'},
{'.','.','.','.','8','.','.','7','9'}};
cout << s.isValidSudoku(board) << endl;
board = {
{'8','3','.','.','7','.','.','.','.'},
{'6','.','.','1','9','5','.','.','.'},
{'.','9','8','.','.','.','.','6','.'},
{'8','.','.','.','6','.','.','.','3'},
{'4','.','.','8','.','3','.','.','1'},
{'7','.','.','.','2','.','.','.','6'},
{'.','6','.','.','.','.','2','8','.'},
{'.','.','.','4','1','9','.','.','5'},
{'.','.','.','.','8','.','.','7','9'}};
cout << s.isValidSudoku(board) << endl;
return 0;
} 输出:
1
0
3. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:
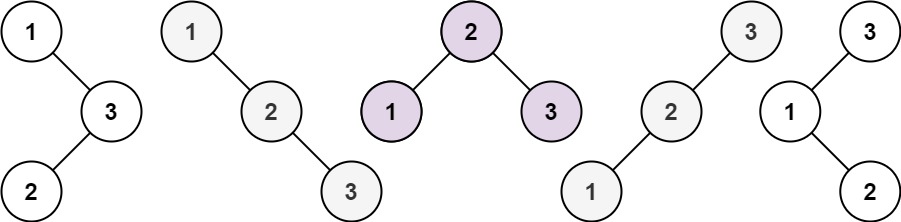
输入:n = 3 输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
1 <= n <= 8
代码:
#include <stdio.h>
#include <stdlib.h>
struct TreeNode
{
int val;
struct TreeNode *left;
struct TreeNode *right;
};
static struct TreeNode *dfs(int low, int high, int *count)
{
int i, j, k;
if (low > high)
{
*count = 0;
return NULL;
}
else if (low == high)
{
struct TreeNode *node = malloc(sizeof(*node));
node->val = low;
node->left = NULL;
node->right = NULL;
*count = 1;
return node;
}
else
{
*count = 0;
int capacity = 5;
struct TreeNode *roots = malloc(capacity * sizeof(struct TreeNode));
for (i = low; i <= high; i++)
{
int left_cnt, right_cnt;
struct TreeNode *left_subs = dfs(low, i - 1, &left_cnt);
struct TreeNode *right_subs = dfs(i + 1, high, &right_cnt);
if (left_cnt == 0)
left_cnt = 1;
if (right_cnt == 0)
right_cnt = 1;
if (*count + (left_cnt * right_cnt) >= capacity)
{
capacity *= 2;
capacity += left_cnt * right_cnt;
roots = realloc(roots, capacity * sizeof(struct TreeNode));
}
for (j = 0; j < left_cnt; j++)
{
for (k = 0; k < right_cnt; k++)
{
roots[*count].val = i;
roots[*count].left = left_subs == NULL ? NULL : &left_subs[j];
roots[*count].right = right_subs == NULL ? NULL : &right_subs[k];
(*count)++;
}
}
}
return roots;
}
}
static struct TreeNode **generateTrees(int n, int *returnSize)
{
int i, count = 0;
struct TreeNode *roots = dfs(1, n, &count);
struct TreeNode **results = malloc(count * sizeof(struct TreeNode *));
for (i = 0; i < count; i++)
{
results[i] = &roots[i];
}
*returnSize = count;
return results;
}
static void dump(struct TreeNode *node)
{
printf("%d ", node->val);
if (node->left != NULL)
{
dump(node->left);
}
else
{
printf("# ");
}
if (node->right != NULL)
{
dump(node->right);
}
else
{
printf("# ");
}
}
int main(int argc, char **argv)
{
if (argc != 2)
{
fprintf(stderr, "Usage: ./test n\n");
exit(-1);
}
int i, count = 0;
struct TreeNode **results = generateTrees(atoi(argv[1]), &count);
for (i = 0; i < count; i++)
{
dump(results[i]);
printf("\n");
}
return 0;
}
附录
二叉搜索树
又称二叉查找树或二叉排序树,BST,Binary Search Tree。一棵二叉搜索树是以二叉树来组织的,可以使用一个链表数据结构来表示,其中每一个结点就是一个对象。一般地,除了key和位置数据之外,每个结点还包含属性lchild、rchild和parent,分别指向结点的左孩子、右孩子和双亲(父结点)。如果某个孩子结点或父结点不存在,则相应属性的值为空(NULL)。根结点是树中唯一父指针为NULL的结点,而叶子结点的孩子结点指针也为NULL。
二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点,又有数组快速查找的优势;例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
二叉搜索树能够高效地进行操作:1.插入一个数值;2.查询是否包含某个数值;3.删除某个数值。
性质
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点,那么y.key≤x.key。如果y是x右子树中的一个结点,那么y.key≥x.key。
在二叉搜索树中:
1.若任意结点的左子树不空,则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空,则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
复杂度
不论哪一种操作,所花的时间都和树的高度成正比。因此,如果共有n个元素,那么平均每次操作需要O(logn)的时间。
算法实现
二叉排序树的操作主要有:
1.查找:递归查找是否存在key。
2.插入:原树中不存在key,插入key返回true,否则返回false。
3.构造:循环的插入操作。
4.删除:
(1)叶子节点:直接删除,不影响原树。
(2)仅仅有左或右子树的节点:节点删除后,将它的左子树或右子树整个移动到删除节点的位置就可以,子承父业。
(3)既有左又有右子树的节点:找到须要删除的节点p的直接前驱或者直接后继s,用s来替换节点p,然后再删除节点s。


![③【Java 组】蓝桥杯省赛真题 [黄金连分数][马虎的算式]持续更新中...](https://img-blog.csdnimg.cn/20a7f1b58dfb4660b75d7f021c157d57.png#pic_center)