前言
在这篇文章中,荔枝会整理一下自己学习二叉树的学习笔记。主要内容包括树与二叉树的基本定义以及基础概念、二叉树的存储结构、二叉树的四种遍历方法以及二叉查找树的基本内容。
文章目录
前言
一、树形存储结构
二、二叉树
2.1 二叉树的基本定义
2.2 二叉树的存储结构
2.2.1 顺序存储结构
2.2.2 链式存储结构
2.3 二叉树的遍历
2.3.1 先序遍历
2.3.2 中序遍历
2.3.3 后序遍历
2.3.4 层次遍历
三、二叉搜索树BST
3.1 二叉搜索树的查找
3.2 二叉搜索树的插入
3.3 二叉搜索树的删除
总结
一、树形存储结构
树是一种非线性存储结构,主要的逻辑关系是一对多,从外形上看其实就相当于数目的根系。在树这一结构中的所有元素都可以称之为结点。结点之间的关系为父结点和子结点,没有父结点的结点称之为根结点;没有子结点的结点称之为叶结点。那么一个树可以看成为一个根结点和若干个子树构成,这若干个子树组成森林,因此一个树形结构可以看成一个根节点和森林组成。一个结点拥有的子树的个数称之为结点的度,树中结点层级的最大值被称为树的高度或深度。
二、二叉树
2.1 二叉树的基本定义
定义一个二叉树需要满足两个条件,首先需要是有序树,同时各个结点的度不超过2。通俗一点讲,在一个树形的数据结构中,如果该结构的任意节点的子节点个数不超过2且左右节点分支不能交换的就可以称之为二叉树。二叉树又分为:满二叉树和完全二叉树。
完全二叉树
树的末端最后一层结点是按照从左到右来分布的。
2.2 二叉树的存储结构
2.2.1 顺序存储结构
在二叉树的顺序存储结构中我们可以对一个结点进行编号为N,则其父节点就是N/2,子节点中的左节点为2N,右节点为2N+1。二叉树的顺序存储结构只能用于完全二叉树的应用。
特点:
对于完全二叉树来说,其顺序存储十分合适,但对于一般二叉树来说顺序存储结构会浪费系统较多的存储空间,但其对于寻找一个结点的双亲和孩子比较容易。
2.2.2 链式存储结构
链式存储结构采用了链表这一数据结构作为基础存储,而且是双向链表,每一个子结点均拥有头指针和尾指针头指针指向左结点,右指针指向右结点。

特点:
除了指针外,二叉树比较节省存储空间,占用的空间大小只与节点的数量有关;在链式存储结构中,找一个结点的孩子很容易,找其双亲很难。
2.3 二叉树的遍历
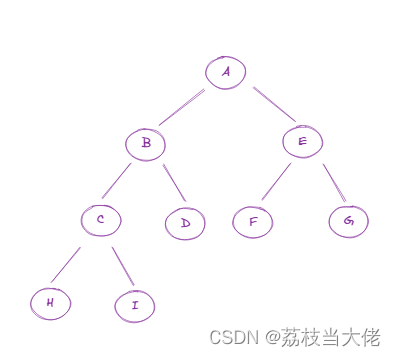
二叉树的遍历主要有四种方法:先序遍历、中序遍历、后序遍历和层次遍历。以一个二叉树ABCDEFGHI为例,我们对比看看四种遍历方式
2.3.1 先序遍历
先序遍历其实比较简单,遍历过程从根结点A开始,遵循先左后右的规则在二叉树中进行遍历。依次遍历A-B-C-H-I-D-E-F-G。在先序遍历中我们可以看出整个过程子结点的遍历顺序和根结点是一样的,因此我们可以考虑使用递归的方法来实现遍历的过程,而递归的结束条件就是当前结点不再有子结点,也就是当前结点是叶结点。前序遍历的过程其实就是不断执行从根节点到子节点的遍历
2.3.2 中序遍历
中序遍历其实就是从当前的结点位置出发,首先进入结点的左子树进行遍历,依旧遵照这先左后右的规则首先进入左结点,若该子结点只有一层子树,继续进入子树结构并访问到左子树结点,结束访问左子结点之后会重新访问该结点,再接着向右侧子树进行遍历。遍历过程依次是:H-C-I-B-D-A-F-E-G。
2.3.3 后序遍历
后序遍历的过程可以理解为和前序遍历的过程是相反的,前序遍历其实就是从根结点到叶结点,但后续遍历则是从叶结点到根结点。比如在上面那张图的二叉树中,我们遍历树中所有的元素的顺序是:H-I-C-D-B-F-G-E-A。具体过程是我们根据先左后右的规则借助不同层级的结点进入到最高层级的叶结点处并执行访问,在该层级中访问到所有的元素之后就会回退到上一层级C的结点并进入该结点的右子树执行重复操作,当完全访问完C所有的子树后就会回退到C并执行访问,对于不同层级之间都是以这种机制来执行回退访问的。
PS:不管是先序、中序还是后序排序,递归的终止条件其实都是当该结点是叶结点的时候不进行递归操作,直接输出并决定是否需要回退。
2.3.4 层次遍历
层次遍历用链表存储的二叉树,可以借助队列存储结构来实现。整个层次遍历过程其实是首先根结点入队,并进入下一层级找到子节点按照从左至右的方式入队,将上述的二叉树进行层次遍历的过程:A-B-E-C-D-F-G-H-I。
三、二叉搜索树BST
二叉搜索树又称之为二叉查找树、有序二叉树、排序二叉树,二叉查找树相比于其它的数据结构的优势在于查找、插入的时间复杂度比较低,二叉查找树可用于构建更为抽象的数据结构,比如集合、多重集和关联数组。最好最坏的时间复杂度都是O(n)。
特点:
若任意结点的左右结点不为空,则左子树上的所有结点的值均小于他的根结点的值;右子树的值均大于或等于其根结点的值。值得注意的是:二叉查找树是没有重复的结点的。
3.1 二叉搜索树的查找
根据二叉搜索树的特殊结构,我们可以直接将要查询的数字num与根结点p进行比较,若num<p,我们就选择p的左结点作为p来跟查询的num比较;若num>p,我们就选择p的右结点作为p来跟查询的num比较,直到找到结点的位置。
3.2 二叉搜索树的插入
二叉搜索树的插入过程和查找的过程其实是类似的,当我们在二叉搜索树搜索的数值并不在树中存储的时候,查找的结点会结束于一条空链这时候就会执行插入的操作。同时也会遵守左小右大的规则进行插入。比如要对num执行插入的操作,那么直接将num于根结点进行比较,如果根结点的值p比nu大,则将num插入左子树中,若左子树为空树,那么num就会以p的左节点的形式存在于二叉树中;对于num大于p的情形也大致相同。
3.3 二叉搜索树的删除
二叉搜索树的删除操作要比查找和插入的操作更加复杂,二叉搜索树的删除主要分为三种情况:要删除的结点P无子节点、要删除的结点P只有一个子结点、要删除的结点P有两个子节点。我们分别看看这三种情况:第一种是最简单的情况,直接将指向P的父节点指针指向null;第二种情况需要将P的父节点指针指向P的子节点;第三种情况最为复杂,我们需要找到P的右子树的最小结点或者是左子树的最大结点并将P的父节点的指针指向该结点。
再来看一下大佬的代码辅助理解:
public class BinarySearchTree {
private Node tree;
/**
* 查找
* @param data
* @return
*/
public Node find(int data) {
Node p = tree;
while (p != null) {
if (data < p.data) p = p.left;
else if (data > p.data) p = p.right;
else return p;
}
return null; //没有找到
}
/**
* 插入
* @param data
*/
public void insert(int data) {
if (tree == null) {
tree = new Node(data);
return;
}
Node p = tree;
while (p != null) {
if (data > p.data) {
if (p.right == null) {
p.right = new Node(data);
return;
}
p = p.right;
} else { //data < p.data
if (p.left == null) {
p.left = new Node(data);
return;
}
p = p.left;
}
}
}
/**
* 删除
* @param data
*/
public void delete(int data) {
Node p = tree; //p 指向要删除的结点,初始化指向根节点
Node pp = null; //pp 记录的是 p 的父节点
while (p != null && p.data != data) {
pp = p;
if (data > p.data) p = p.right;
else p = p.left;
}
if (p == null) return; //没有找到
//要删除的节点有两个子节点
if (p.left != null && p.right != null) {//查找右子树中最小的节点
Node minP = p.right;
Node minPP = p; //minPP 表示 minP 的父节点
while (minP.left != null) {
minPP = minP;
minP = p.left;
}
p.data = minP.data; //将 minP 的数据替换到 p 中
p = minP; //下面就变成了删除 minP 了,要结合整个删除函数来看
pp = minPP;
}
//删除的是叶子节点或者仅有一个子节点
Node child; //p 的子节点
if (p.left != null) child = p.left;
else if (p.right != null) child = p.right;
else child = null;
if (pp == null) tree = child; // 删除的是根节点
else if (pp.left == p) pp.left = child;
else pp.right = child;
}
/**
* 查找最小节点
* @return
*/
public Node findMin() {
if (tree == null) return null;
Node p = tree;
while (p.left != null) {
p = p.left;
}
return p;
}
/**
* 查找最大节点
* @return
*/
public Node findMax() {
if (tree == null) return null;
Node p = tree;
while (p.right != null) {
p = p.right;
}
return p;
}
private static class Node {
private int data;
private Node left;
private Node right;
public Node(int data) {
this.data = data;
}
}
}
附上代码原文链接:
https://www.jianshu.com/p/d1133ef8bc0e
总结
在这篇文章中,荔枝主要做了一下有关二叉树的笔记,希望不久之后我也能写一个完整功能的二叉树哈哈哈,个人感觉要掌握新的算法或者数据结构还是得不断地在刷题中掌握知识,总之荔枝会努力向大佬学习的🤩
今朝已然成为过去,明日依然向往未来!我是小荔枝,在技术成长的路上与你相伴,码文不易,麻烦举起小爪爪点个赞吧哈哈哈~~~ 比心心♥~~~