【人脸识别】DDL：数据分布知识蒸馏思想，提升困难样本（遮挡、低分辨率等）识别效果

论文题目：《Improving Face Recognition from Hard Samples via Distribution Distillation Loss》
论文地址：https://arxiv.org/pdf/2002.03662v3.pdf
代码地址：https://github.com/HuangYG123/DDL

1.前言及相关工作

Large facial variations are the main challenge in face recognition。
目前人脸识别面临的主要挑战是大的面部变化（遮挡、姿态如侧脸、低分辨率、种族、光照等）。

解决方式及缺点：

variation-specific：在设计特殊网络损失之前充分利用了与任务相关的方法，即针对不同的问题设计特定的算法。如姿态（pose-invatiant、face frontalization），分辨率（super- resolution），遮挡模型等。
缺点：在不同的任务和场景中通常是不通用的。
generic methods：侧重于提高特征可辨别性以最小化类内距离同时最大化类间距离。如margin-based loss（cosface、arcface），metric learning（triplet loss）等。
缺点：在简单样本上表现良好但在困难样本上表现不佳。

DDL：
为了提高困难样本的性能，我们提出了一种新颖的 Distribution Distillation Loss （分布式蒸馏）来缩小简单样本和困难样本之间的性能差距，该方法简单、有效且通用，适用于各种类型的面部变化。具体来说，我们首先采用最先进的分类器（如 Arcface）来构建两个相似性分布：来自简单样本的教师分布（例如图1中d3的简单样本）和来自困难样本的学生分布（例如图1中d1的困难样本）。然后，我们提出了一种新的分布驱动损失来约束学生分布以近似教师分布，从而实现学生分布中正负对之间的重叠更小。

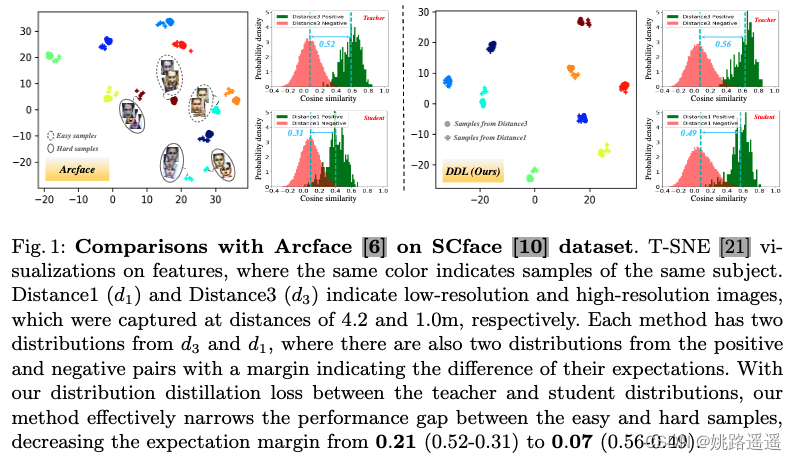
在这里插入图片描述
如图 1 所示，最先进的 (SotA) 面部分类器，如 Arcface [6]，可以很好地处理特征空间中具有紧密分组的小变化图像。我们将这些表示为简单样本。相比之下，具有较大变化的图像通常与特征空间中的简单图像相距甚远，并且更难处理。我们将这些表示为困难样本。在图1中，相同的颜色表示同一主题的样本。 Distance1 (d1) 和 Distance3 (d3) 表示分别在 4.2 和 1.0m 的距离处捕获的低分辨率和高分辨率图像。每种方法都有来自 d3 和 d1 的两个分布，其中也有来自正负对的两个分布，margin表示它们的期望差异。通过我们在教师和学生分布之间的分布蒸馏损失，我们的方法有效地缩小了简单样本和困难样本之间的性能差距，将期望差从 0.21 (0.52-0.31) 降低到 0.07 (0.56-0.49)。

知识蒸馏相关：
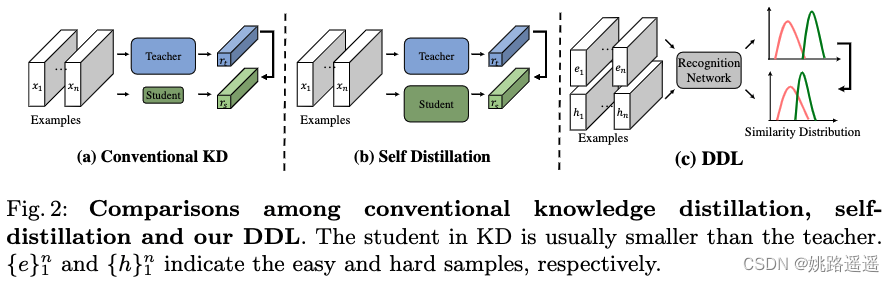
在这里插入图片描述
与传统蒸馏方法相比， DDL 在几个方面有所不同（见图 2）：

KD 至少有两个网络，一个老师和一个学生，而 DDL 只学习一个网络。尽管在 KD中，学生可能具有与教师相同的结构（例如，自蒸馏），但他们在训练中具有不同的参数。
KD使用sample-wise、Euclidean distance-wise或anglewise约束，而DDL提出了一种新的余弦相似度分布约束，专为人脸识别设计。
据我们所知，目前没有 KD 方法在人脸基准上优于 SotA 人脸分类器，而 DDL 始终优于 SotA Arcface 分类器。

2.DDL

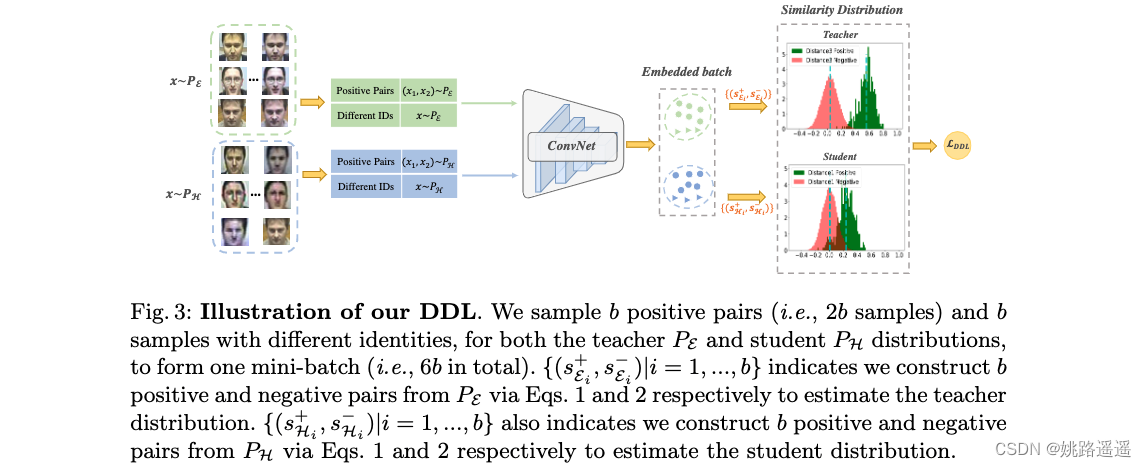
在这里插入图片描述

上图为 DDL 的框架。我们将训练集分为两部分，即 E 表示简单样本，H 表示困难样本，分别形成教师和学生分布。通常，对于训练期间的每个小批量，我们从两个部分进行采样。为了确保良好的教师分布，我们使用 SotA FR 模型 [6] 作为我们的初始化。提取的特征用于构建正负对（第 3.1 节），它们进一步用于估计相似性分布（第 3.2 节）。最后，基于相似性分布，所提出的 DDL 用于训练分类器（第 3.3 节）。

2.1.Sampling Strategy from PE and PH

首先，我们介绍了在训练过程中如何在一个mini-batch中构建正负对的细节。给定来自 PE 和 PH 的两种输入数据，每个 mini-batch 由四部分组成，两种正对（即 (x1, x2) ∼ PE 和 (x1, x2) ∼ PH），以及两种具有不同身份的样本（即 x∼PE 和 x∼PH）。具体来说，我们一方面构造 b 个正对（即 2b 个样本），另一方面构造 b 个来自 PE 和 PH 不同身份的样本。结果，每个 mini-batch 中有 6b = (2b + b) * 2 个样本（更多细节见图 3）。

2.1.1.Positive Pairs

正对是预先离线构建的，每对由两个具有相同身份的样本组成。如图 3 所示，每个正对的样本按顺序排列。通过深度网络F将数据嵌入到高维特征空间后，可以得到正对s+的相似度如下：
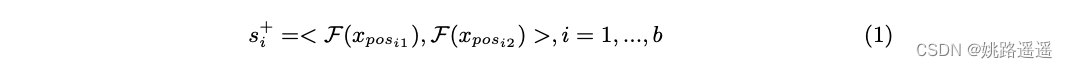
在这里插入图片描述
其中 xposi1 、 xposi2 是一对正样本。请注意，相似度小于 0 的正对通常是异常值，由于我们的主要目标不是专门处理噪声，因此将其作为实际设置删除。

2.1.1.Negative Pairs

与正对不同，我们通过困难负样本挖掘从具有不同身份的样本在线构建负对，它选择具有最大相似性的负对。具体来说，负对s−的相似度定义为：
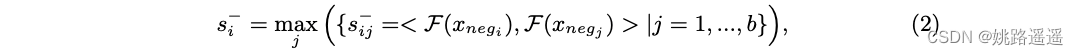
在这里插入图片描述
其中 xnegi ， xnegj 来自不同的ID。一旦构造了正负对的相似性，就可以估计相应的分布。

2.2.Similarity Distribution Estimation

       相似性分布估计的过程类似于[37]，它使用具有软分配的一维直方图以简单且分段可微分的方式执行。具体来说，来自同一个人的两个样本xi，xj组成正对，对应的标签记为mij = +1。相反，来自不同人的两个样本形成负对，标签表示为 mij = -1。然后，我们得到两个样本集 S+ = {s+ = 〈F (xi), F (xj)〉|mij = +1} 和 S− = {s− = 〈F (xi), F (xj)〉|mij = −1} 分别对应于正负对的相似性。
       令 p+ 和 p− 分别表示 S+ 和 S− 的两个概率分布。与基于余弦距离的方法 [6] 一样，每对的相似性限制为 [−1, 1]，这被证明可以简化任务 [37]。受直方图损失的启发，我们通过用均匀间隔的 bin 拟合简单直方图来估计这种类型的一维分布。我们采用 R 维直方图 H+ 和 H−，节点 t1 = −1, t2, … , tR = 1 均匀填充 [−1, 1]，步长为 2 / R−1。然后，我们估计直方图 H+ 在每个 bin 的值 h+r 为：
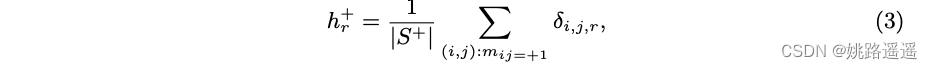
在这里插入图片描述
       其中 (i, j) 跨越所有正对。与 [37] 不同，权重 δi,j,r 由指数函数选择为：

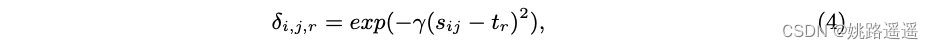
在这里插入图片描述
其中 γ 表示高斯核函数的扩展参数，tr 表示直方图的第 r 个节点。我们采用高斯核函数，因为它是最常用的密度估计核函数，并且对小样本量具有鲁棒性。 H− 的估计类似地进行。

2.3.Distribution Distillation Loss

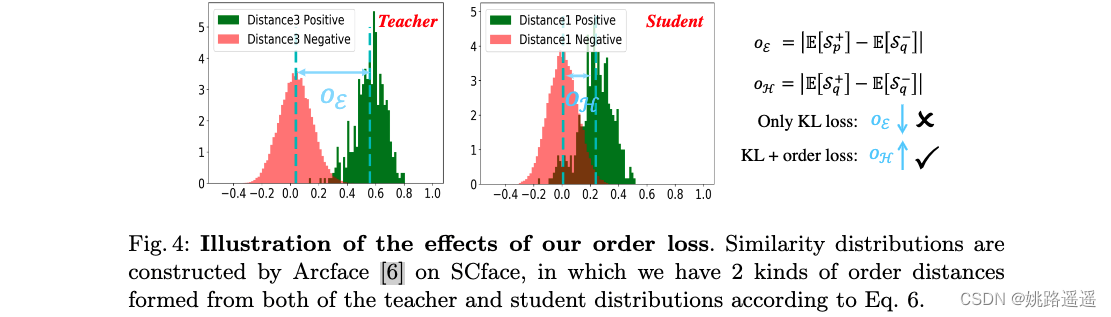
在这里插入图片描述

我们利用 [6] 等 SotA 人脸识别引擎，从两种样本中获取相似度分布：简单样本和困难样本。这里，easy samples 表明 FR engine 表现良好，其中正负对的相似度分布明显分开（参见图 4 中的教师分布），而 hard samples 表明 FR engine 表现不佳，其中相似性分布可能高度重叠（参见图 4 中的学生分布）。

2.3.1.KL Divergence Loss

为了缩小简单样本和困难样本之间的性能差距，我们将困难样本的相似性分布（即学生分布）约束为近似简单样本的相似性分布（即教师分布）。教师分布由正对和负对的两个相似性分布组成，分别表示为 P + 和 P - 。类似地，学生分布也由两个相似性分布组成，表示为 Q+ 和 Q−。受先前 KD 方法 [12, 53] 的启发，我们采用 KL 散度来约束学生和教师分布之间的相似性，其定义如下（其中 λ1, λ2 是权重参数）：
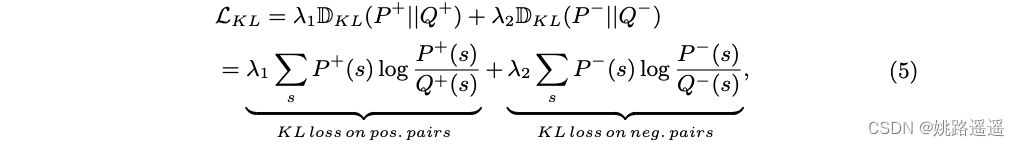
在这里插入图片描述

2.3.2.Order Loss

然而，仅使用 KL 损失并不能保证良好的性能。事实上，教师分布可能会选择接近学生分布，并导致正对和负对分布之间出现更多混淆区域，这与我们的目标相反（见图 4）。为了解决这个问题，我们设计了一个简单而有效的术语，称为 order loss，它最小化负对和正对的相似性分布期望之间的距离，以控制重叠。我们的order loss可以表述如下：

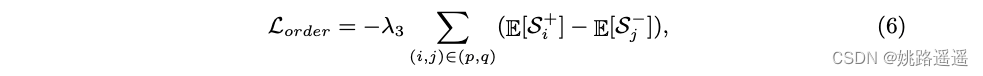
在这里插入图片描述
其中 S+ p 和 S− p 表示教师分布的正负对的相似度； S+ q 和 S− q 表示学生分布的正负对的相似度； λ3 是权重参数。
总之，我们的分布蒸馏损失的整个公式是：LDDL = LKL + Lorder。 DDL 可以很容易地扩展到多个学生分布，从一个特定的变体变化如下：

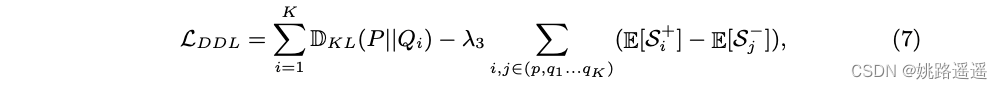
在这里插入图片描述
其中 K 是学生分布的数量。此外，为了保持简单样本的性能，我们结合了 Arcface [6] 的损失函数，因此最终损失为：

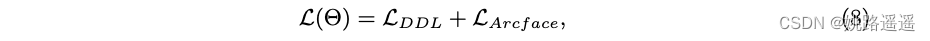
在这里插入图片描述
其中 Θ 表示参数集。请注意，LArcface 可以很容易地替换为 FR 中任何一种流行的损失。

2.4.Generalization on Various Variations

接下来，我们讨论 DDL 在各种变体上的泛化，它定义了我们的应用场景以及我们如何选择简单/困难样本。基本上，我们可以根据图像是否包含可能阻碍身份信息的大面部变化（例如，低分辨率和大姿势变化）来区分简单和困难样本。

2.4.1.Observation from Different Variations

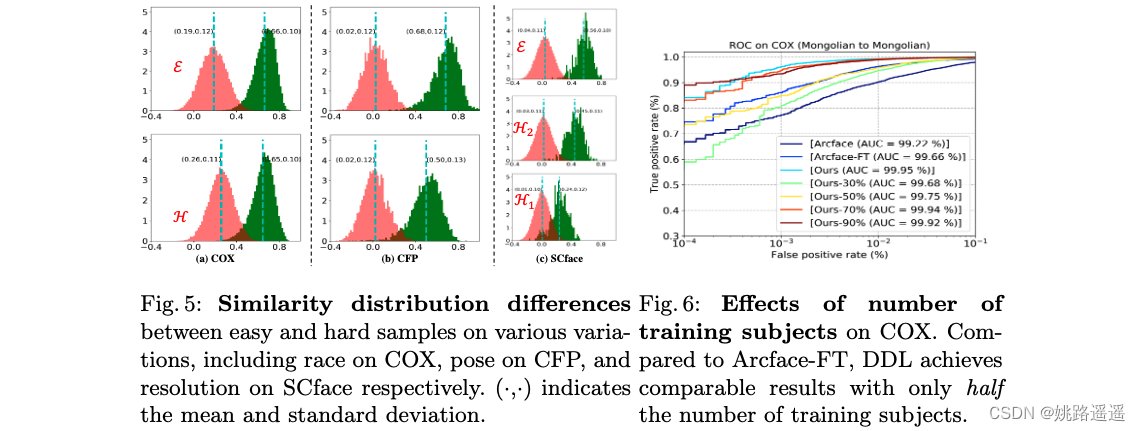
在这里插入图片描述

我们的方法假设两个或多个分布，每个分布都是从训练数据的一个子集计算出来的，它们之间存在差异，这是人脸识别中的一种普遍现象，如图 5 所示。它显示了正常和具有挑战性的样本的相似性分布基于 Arcface [6] 在 CASIA 上训练，除了 CFP，它在 VGGFace2 上训练。正如我们所见，1）由于 CASIA 偏向高加索人，COX 中的蒙古样本更难，因此相对被视为困难样本，2）不同的变化有一个共同的观察结果，即具有挑战性的样本的相似性分布通常与那些样本不同简单样本的数量，3）不同程度的变化可能具有不同的相似性分布（例如，图 5（c）中的 H1 和 H2）。总之，当一项任务满足简单样本和困难样本之间的相似性分布不同时，我们的方法是一个很好的解决方案，并且可以通过正确构建正负对来享受性能提升，如4.3节中所验证的那样。

2.4.2.Performance Balance Between Easy and Hard Samples

提高困难样本的性能同时保持简单样本的性能是一种权衡。我们方法中的两个因素有助于保持简单样本的性能。首先，我们结合了 SotA Arcface 损失 [6] 来保持简单样本的特征可辨别性。其次，我们的order loss最小化了负对和正对的相似性分布期望之间的距离，这有助于控制正负对之间的重叠。

2.4.3.Discussions on Mixture Variations.

如公式（7）所示，我们的方法可以很容易地扩展到一项任务的多种变体（例如，低分辨率、大姿势等）。另一种方法是将一项任务的不同程度的变化混合到一个学生分布中，如第 4.2 节所示、对不同程度的具体建模不够好，容易导致性能下降。对于不同任务的不同变化，也可以构建多个师生分布对分别解决相应的任务，这不失为一个很好的未来方向。