目录
1.什么是树
1.1浅显的理解树
1.2 数据结构中树的概念
2.树的各种结构概念
2.1 节点的度
2.2 根节点/叶节点/分支节点
2.3 父节点/子节点
2.4祖先节点/子孙节点
2.5兄弟节点
2.6树的度
2.7节点的层次
2.8森林
3. 如何用代码表示一棵树
3.1链式结构
3.1.1 树节点的定义方式1(指针数组)
3.1.2 树节点的定义方式2(左孩子右兄弟表示法)
3.2数组结构
3.2.1 每个节点存父亲下标
3.2.2 完全二叉树的数组表示法
1.什么是树
1.1浅显的理解树

树,其实就是我们现实中的树(注意看有好多分支),但是现在这棵树是一个数据结构!
在数据结构当中,我们设计结构的目的是为了存储数据,我们所说的树亦是一个能存数据的树。或者更准确的说,是一个一个的数据按照树型结构组织在了一起。那这是一种什么样的数据结构呢?
之前了解到的数据结构,如顺序表,链表等,他们都是线性的存储结构,即一个数据连接着下一个数据,在逻辑上上是呈现线性的。而树这种数据结构则不同,所有数据组织在一起的方式并不是一条单纯的直线了,而是一个树形。
1.2 数据结构中树的概念
树是一种非线性的数据结构,它由一个一个的有限数量的节点组织形成,本质上就是节点的集合。在实际coding当中,一棵树是一个倒挂的树,即root树根是在最上层,叶子在最底层。
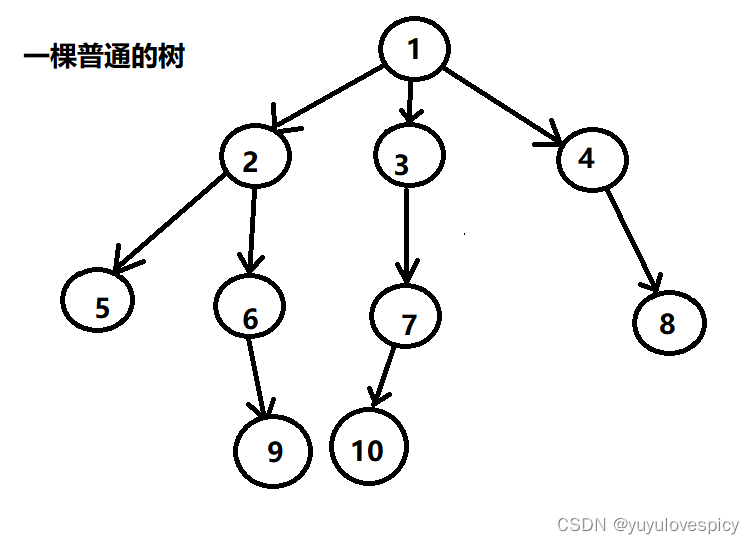
所以实际上我们数据结构中的树是一棵倒挂的树,根在最上面。

树当中,有一个特殊的节点,就是根节点,除了空树,每一棵树都有根节点,根节点是唯一的,根节点之上没有其他的节点。
每一棵树,都可以这样划分:根 根的子树1,子树2,子树3 ........ 子树n(n是看根有多少棵直接子树)。
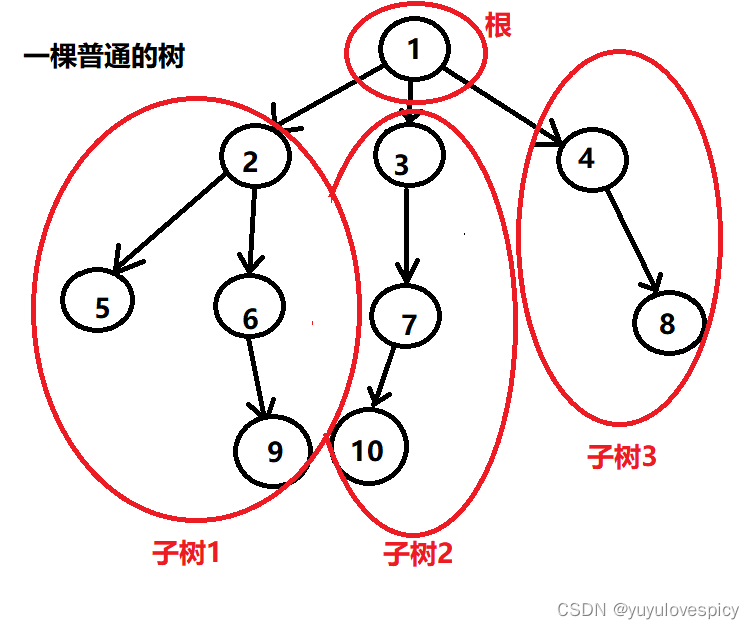
每一棵子树,也都是一棵树。也可以分为子树的根,子树根 的 子树1,子树2......子树n。
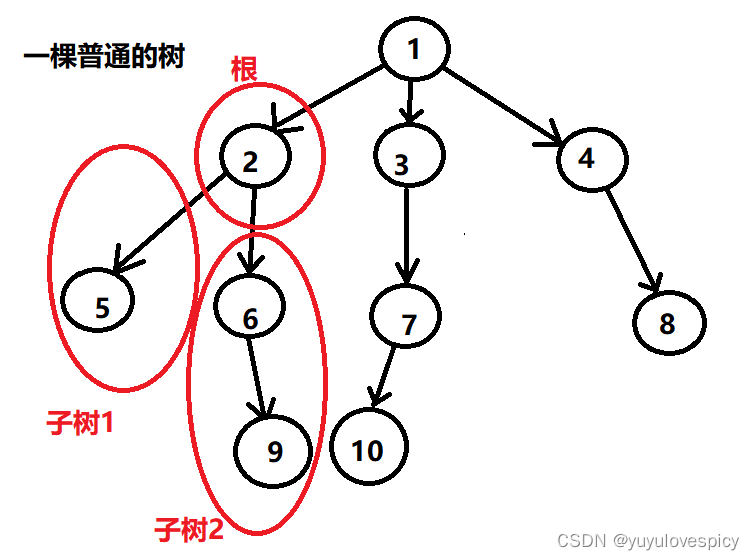
按照这个思路,一棵树由根 + 所有的的每一颗子树,组成划分的;根的每一棵子树,也都是按 根 + 所有的每一颗子树构建的;所有的子树的子树,也都是按 根 + 所有的的每一颗子树 方式组织的;所有的子树的子树的子树(此处省去一万字)。。。。。。
所以树本质上都是通过递归定义的。
2.树的各种结构概念
2.1 节点的度
节点的度,就是一个节点的子树的个数,或者说,就是一个节点有几个分叉。

如上面 1节点,它的度就是3(有3个子树/分叉 2 3 4);2节点,它的度是2(有2个子树/分叉 5 6);7节点,它的度是1(只有一个子树/分叉)。
2.2 根节点/叶节点/分支节点
根节点:就是最开始的一个节点(如图的 1节点),它是唯一的。从根开始找,这棵树的所有节点都可以遍历找到。所以只要找到了一棵树的根,这棵树就算是被我们所“掌控”。

叶子节点:度为0的节点,即往下没有子树/分支的节点。即我这个节点的下面就没有任何东西了(空),我这个节点就是叶子节点。(如图中的 5 9 10 8,是上图中树的叶子节点)。
分支节点:这是叶子节点的对立,即度不为0的节点,只要不是叶子节点,那你就是分支节点。
2.3 父节点/子节点
父节点:就是一个节点的父亲。就是一个节点上面的那一个节点,如在下图当中,5的父节点是2,10的父节点是7,3的父亲节点是1.。
这里需要着重强调:就像在现实当中任何一个人都只有一个爹,任何一个节点,也都只有一个父节点。(除根节点,根节点没有父亲)
要找到任何一个节点,也只能通过父亲节点找到。父节点,也只能由他的唯一的父亲节点找到,所以其实在树中,要找到任何一个节点都只有唯一的一条路径。

相对于父节点,那父的儿子就是子节点,即父亲往下可以直接找到的节点。就像现实当中,一个爹,都可以有多个儿子,也可以有一个儿子,也可能没有儿子,在树当中,任何一个节点,只要在我这个节点的下面能直接找到的节点,那这就是子节点。
如1的子节点,就是2 3 4节点;2的子节点,就是5 6节点;4的子节点,就只有 8节点。
2.4祖先节点/子孙节点
祖先节点:从根到该节点所经分支上的所有节点,都是祖先节点。类比现实,你爹是你的祖先,你爷爷是你的祖先,你太爷爷是你的祖先……你的太太太太太太太爷爷都是你的祖先。(当然这里我们也可以知道,根节点一定是所有节点的祖先节点)
如6节点的祖先节点是2 1节点;如9节点的祖先节点是6 2 1节点;如8节点的祖先是4 1节点。
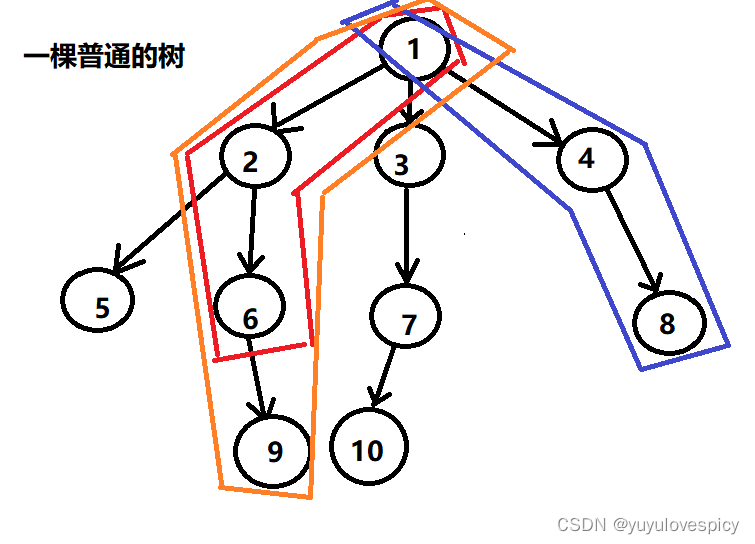
子孙节点:祖先是从根节点找到该节点路径上的所有点,而子孙,其实就是我这个节点能被某个节点所找到!!!即只要,我这个节点只要能往下找到你,我就是祖先,你就是子孙。如2节点作为祖先节点,那5 6 9这三个节点就都是子孙节点。
2.5兄弟节点
兄弟节点:(必须是亲兄弟!!!)有同一个的父节点,我们才是兄弟节点!!!
如下图当中5和6才是兄弟节点,6和7就不是兄弟节点,7和8就不是兄弟节点。

2.6树的度
是一棵树中,所有节点的最大度,称之为树的度。就是所有的节点的度中,挑出其中最大的节点度。PS:最大的节点度,不一定是根节点的度,我们要求的是有最多分支的节点。
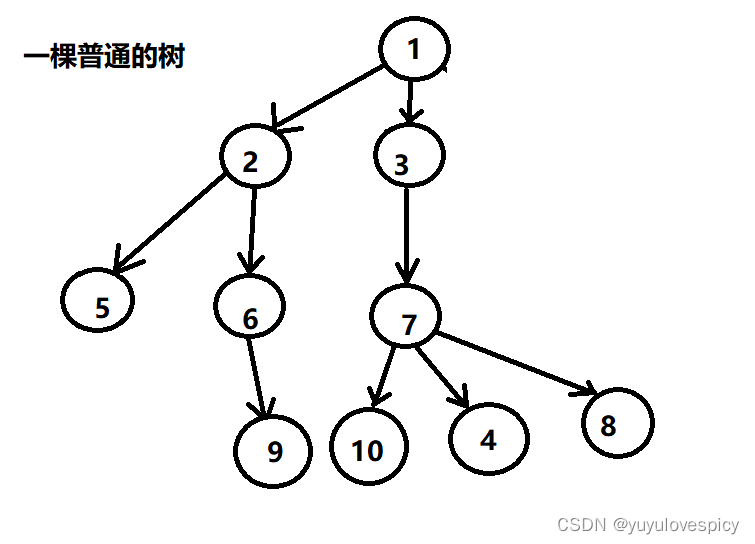
如这棵树,它的度就是3:即7这个节点的度,是所有节点当中度最大的(3,其余节点的度都是2或1或0),所以这棵树的度就是3。
2.7节点的层次
从根开始定义起,根为第1层,根的子节点为第2层。节点的层次也叫树的高度/深度。
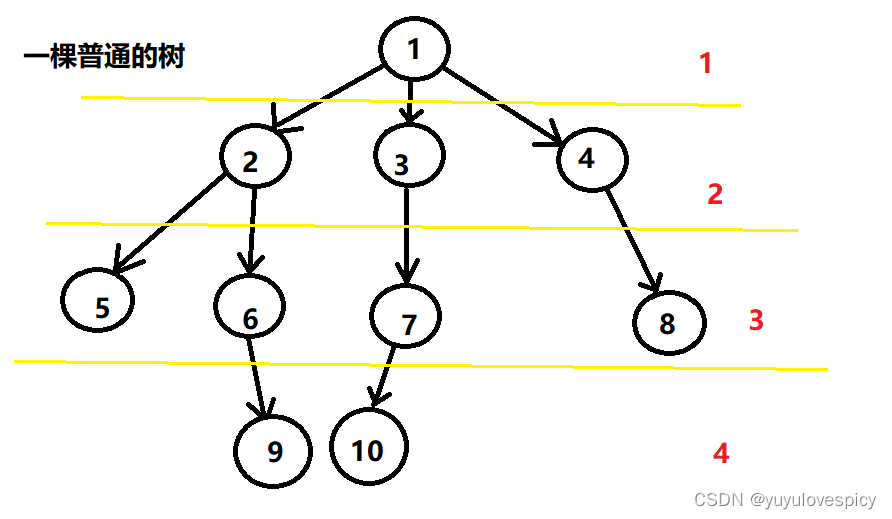
当然也有些地方根是第0层,根的子节点为第1层,即上图分为0 1 2 3层,这样也说的过去。
不过我们还是推荐 1 2 3 4 (如上图画的那样),这样方便理解:
空树是没有根节点,如果我们算根节点为第1层,这样空树的高度我们就可以换定义为0了,更加符合我们的观感!
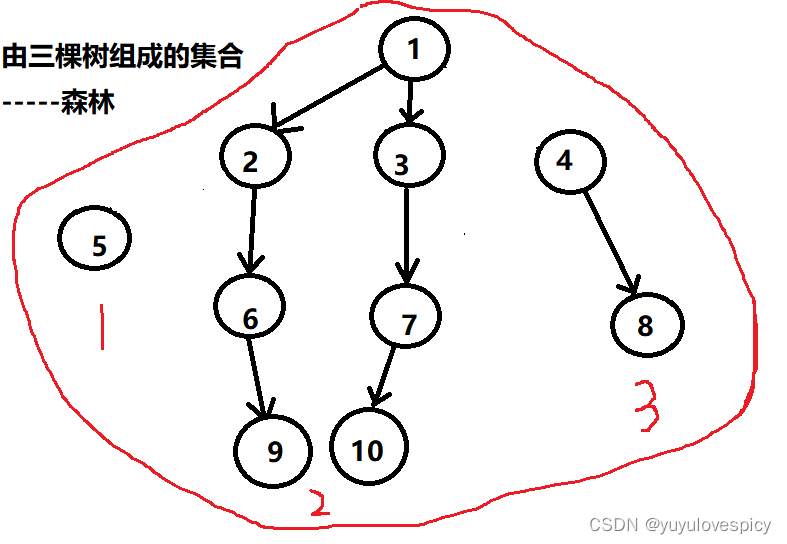
2.8森林
有N(N>0)棵树,即至少一棵 互不相交的树 的集合称为森林。
如并查集这个数据结构就是森林(就是有多棵树嘛)。
3. 如何用代码表示一棵树
刚才我们只是从抽象图上表征了树,那落实到代码当中,一棵树如何用代码来表示呢?我们可以用链式结构来表示一棵树,也可以用数组结构来表示一棵树。
3.1链式结构
要用链式结构来实现树,我们就要首先定义出来一个节点类,因为我们一定是把一个一个的节点链起来组成的一棵树(当然节点与节点之间的链接,我们是通过指针来实现的)。节点是组成树的基础。那如何定义节点类呢?
3.1.1 树节点的定义方式1(指针数组)
我们节点TreeNode要存一个数据data,这个毋庸置疑,然后就是要存储指针,即链接到子节点的链子。那这样就有一个问题,我每个节点的子节点的数量是不一定的,要使用的链子(指针)数量也是不一定的,所以我们要存储多个节点指针。
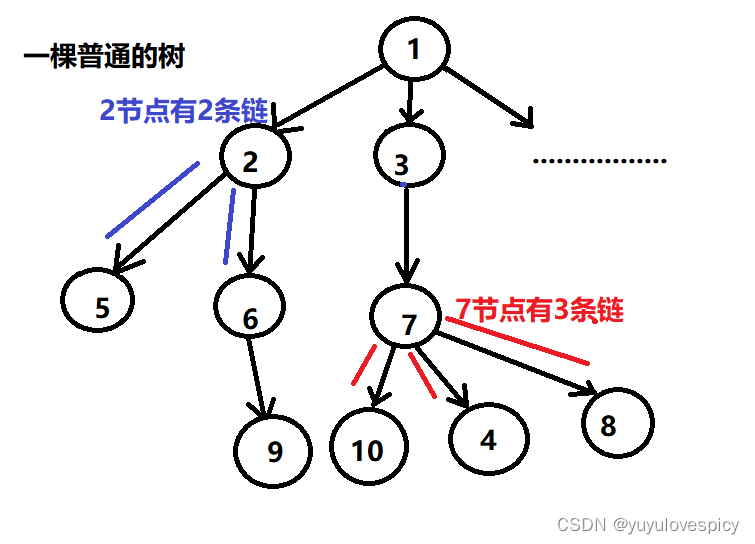
一种方法是让每个节点存储一个指针数组,这个指针数组可以是一个定长的。
struct TreeNode
{
int data;
struct TreeNode* *pSonNode[N];
};但是这种情况是存在缺陷的,如果你知道了这个树的度(即一个节点,最大所能有的分叉数量),或者你规定这个树是固定有多少个叉的,那这个N是可以确定的,可是如果没有给这个度,那N存多大就很难确定了:如果N给大了,那就会造成很多的空间浪费。如果N给小了,有可能导致有的节点,所能链接到的节点数量受限。
所以我们通常是存一个可以动态增长的数组指针,按需给相应大小数量的指针。
struct TreeNode
{
int data;
vector<struct TreeNode*> pTreeSon;
};上面的方法,在指定了这是几叉树 / 该树的度确定,这两种情况下,在节点中直接存储指向孩子的指针,这的确是一种很好的表示树的方法。但是现实中,树的情况是很复杂的,对于度不确定的这种树,我们不推崇上面这个方法,我们有一个也是很好的方法---左孩子右兄弟表示法。
3.1.2 树节点的定义方式2(左孩子右兄弟表示法)
struct TreeNode
{
int data;
struct TreeNode* Left_FirstChild;
struct TreeNode* Right_NextBrother;
};每一个节点,只存,链接到 最左的孩子(即我的第一个孩子)的指针,以及链接到 右边的兄弟(即我旁边的那个亲兄弟节点)的指针。
举个例子:如下图,2节点,我只存储两个指针:我的Left_FirstChild为指向最左边的即第一个孩子5,我的Right_NextBrother为指向我右边的即旁边的亲兄弟3。
再如下图的6节点:我的Left_FirstChild,指向的是第一个孩子9。而我Right_NextBrother,旁边右边的第一个亲兄弟,是空!这里注意哦,兄弟指代的是亲兄弟哦!你只能说6和7是堂兄弟的关系。反正我7节点的右边是没有亲兄弟的,所以Right_NextBrother存NULL。
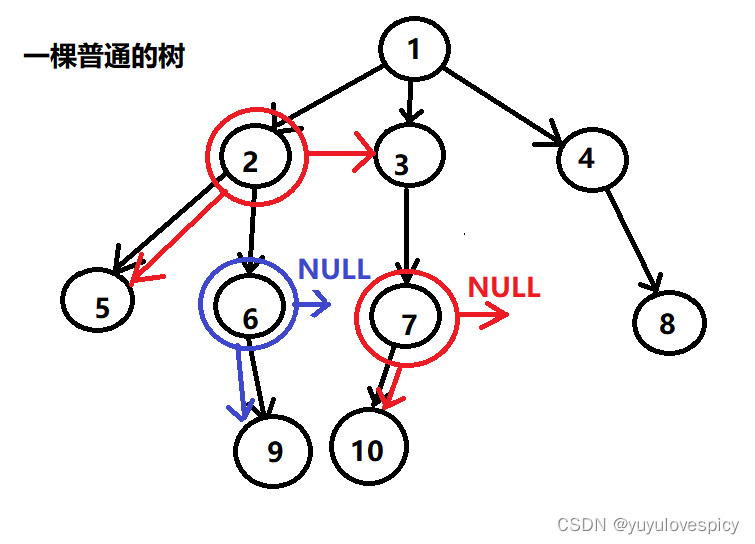
那这样存为什么能够表示整棵树呢? 画个图你就明白了:比如我们要用这个左孩子右兄弟法表示下面这棵树:
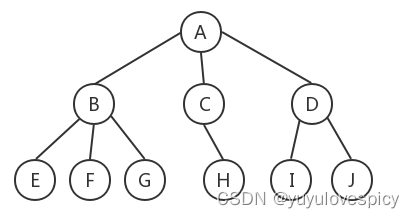
那么如果我们用左孩子右兄弟法,组织节点,组织成这棵树:
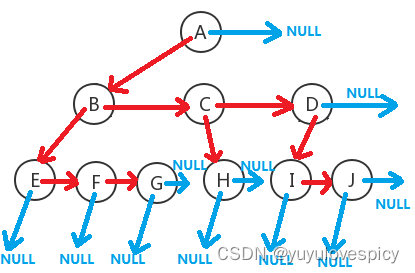
你可以看到,这种方法其实是把每一个节点都建立了被链接关系,即我总是能通过某条路径找到这个节点,我们可以根据左孩子右兄弟法这些安插的链子,找到所有节点。
(只要可以找到/遍历到任何节点,那这就是一种成功的表示树的方法)
例如要找H节点,我们可以通过A的左孩子找到B,然后通过B的右兄弟找到C,然后通过C的左孩子找到H节点;
再例如要找到G节点,我们可以通过A的左孩子找到B,然后通过B的左孩子找到E,然后通过E的右兄弟找到F,然后通过F的右兄弟找到G节点。.
这种方法,相比第一种方法,对于任意树的构建,是没有空间浪费的,而且可以全部遍历找到,非常优!!!
3.2数组结构
没错,我们用一个数组,也可以组织表示一棵树哦!(后面写并查集的时候,一个数组甚至能够表示一个森林,也就是多棵树)是不是很神奇!?下面我们具体看一下如何实现。
3.2.1 每个节点存父亲下标
我们每个节点,即每个节点的数据都存储在一个数组的一个格子当中,这样每一个数据就都有了一个存储下标index,然后这个数组每个格子,不止存数据,还存储着该数据节点的父亲的所在下标(根节点没有父亲,存-1)。这种方法也可以表示整棵树,也即可以遍历到/找到任意的一个节点。何出此言?
struct TreeNode
{
int data; //节点存储的数据
int parent_i;//我这个节点的父亲的在数组的下标
};如果我们要找到任意一个节点,可以选择遍历这个数组,从而找到这个节点;然后如何找到这个从根到这个节点的路径呢?其实我们可以通过这个数组每个格子里面存储的父亲的下标,一直往父亲跳,一直跳到根即可,记录每个跳到的节点,其实这就是从根到该节点的路
径。

如上面这棵树,我们用数组存储父亲下标法,就是这样组织出这棵树的:
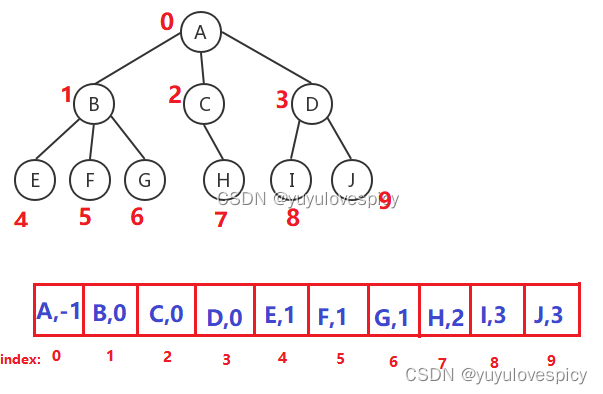
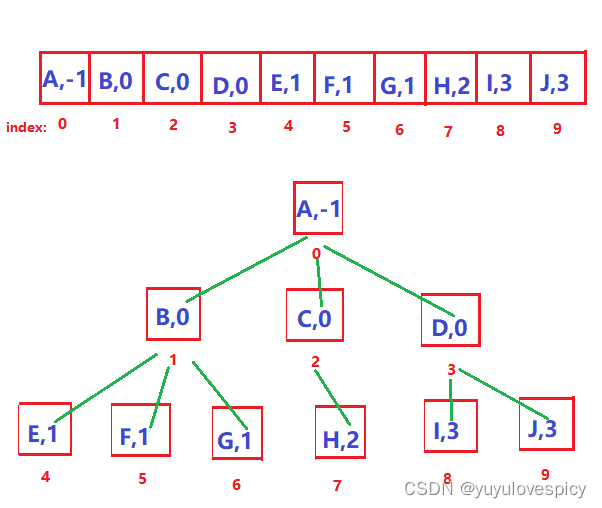
3.2.2 完全二叉树的数组表示法
完全二叉树由于其特殊性,在数组中存储表示可以也是非常方便的,而且也会有很多的性质使用,这个我们会放在后面一篇博客,关于数据结构堆的实现上具体讲解(想了解的话就关注我吧~),这种方法来表示完全二叉树也是非常优秀,非常的劲爆!!!