在很多领域都有“系统”这个概念,它描述的往往是一些复杂关系的总和。假如我们将系统看做一个黑箱,那么,在系统的作用下,外界的输入有时会产生令人意想不到的输出,“蝴蝶效应”就是其中的典型案例。

图1 一只南美洲亚马逊河流域热带雨林中的蝴蝶,偶尔扇动几下翅膀,可以在两周以后引起美国得克萨斯州的一场龙卷风
“蝴蝶效应”的实质是在一个确定性系统中,存在着看似随机的不规则运动,其行为直观表现为不确定性、不可重复、不可预测,即混沌系统。此时将混沌系统理解为黑盒系统是远远不够的,我们需要通过系统的初始状态求解系统未来时刻的状态。
基于同样的原理,我们在Modelica中进行系统建模时,通过求解状态变量确定系统状态,对系统进行动态仿真。假如你还存在如下疑问:
1. 如何实现动态系统建模?
2. 如何规定状态变量?
3. 为什么系统初值非常重要?
4. 怎样建模可以提高系统计算效率?
那么请你一定认真读完本篇技术干货,小编带你全面认识Modelica建模中的状态变量。
一、什么是动态系统?
首先,大家需要理解一点:系统可以分为动态系统和静态系统,状态变量只有在动态系统中才有意义。我们可以举一个简单电路系统的例子,下图分别为只含有电阻的电路与只含有电容的电路,其中u(t)为输出电压,i(t)为输入电流,那么电路系统的方程可以写为如下形式:
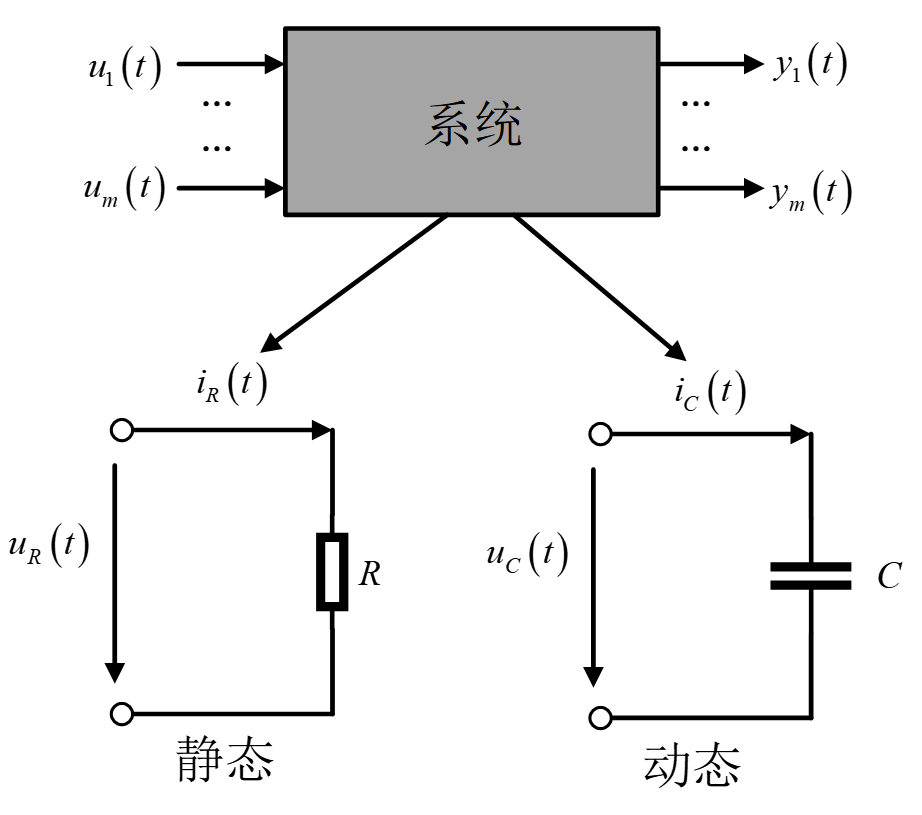
图 2 动态系统与静态系统
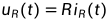
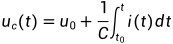
显然,对于含容电路来说,系统的状态受到过去影响随时间变化,这样的系统就被称为动态系统。
二、 什么是状态变量?
状态变量首先由控制学科中引入,定义为动态系统的状态变量为确定动态系统的最小一组变量。只要知道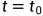 时刻这组变量以及
时刻这组变量以及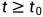 时的输入,就可以完全确定系统的在任何
时的输入,就可以完全确定系统的在任何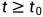 时刻的行为。
时刻的行为。
那么,由这些状态变量组成的一个向量称为状态向量,而状态向量存在的空间称为状态空间。动态系统的任何状态都可以用状态空间中的一个点来表示,动态系统的状态变化可以描述为状态矢量端点随时间变化描绘出的路径。
上述定义有些抽象复杂,下面举一个简单案例以帮助大家理解。将一封闭容腔中装满水并且对水进行加热,若已知水的压力和温度,我们就可以推断出当前水的状态是液态还是气态,还可以计算出当前水的密度、粘度等参数。此时,压力与温度就构成了当前封闭容腔系统的一组状态变量。

图 3 烧水也是一门技术活
那么,微分方程中状态变量是如何表示的呢?
如果只考虑集中参数模型,不同领域工程物理系统的物理本构通常由常微分方程(Ordinary Differentical Equations-ODE)描述,系统组件之间的约束一般用代数方程(Algebraic Equations)表示。
但是对于Modelica 语言,其面向对象的建模特点导致物理本构体现在其组件的建模上,组件之间的约束以连接器的连接方式表现。此时,表达本构模型的微分方程与连接转化的代数方程之间耦合将形成一般形式的微分-代数方程 ( Differentical - AlgebraicEquations -DAE)。
一般来说,常微分方程组可以表示为以下形式:

由于因变量x的导数以独立瞬态变量t和因变量x的形式显式表示,此时将数组视为一组状态变量,只要函数f具有足够的连续性,总能找到初值问题的唯一解。
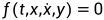
例如:
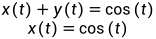
对于微分-代数方程组,导数一般没有显式表示,甚至一些因变量的导数可能不出现在这些方程中。而在表达式中不显式包含变量y的任何导数的变量,这些变量称为代数变量。
在微分-代数方程组中,我们同样选取x为状态变量,但是与常微分方程组不同的是,微分代数方程组内数组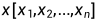 的各分量之间可能存在隐式的约束关系,需要通过选择数组的部分分量作为系统的状态变量。
的各分量之间可能存在隐式的约束关系,需要通过选择数组的部分分量作为系统的状态变量。
总而言之,我们可以得出一条规律,状态变量的一大特征是其对时间的导数已知。即:

而对于Modelica语言,其实质是解决微分-代数方程问题,在求解前需要对微分-方程系统的状态变量进行选择。
三、如何通过状态变量描述系统?
引言中我们提到了将系统看做一个黑盒模型,输入变量经过与黑盒的交互产生输出。通过上述的状态空间方法,我们可以推导其输入、输出与状态变量之间的表达式。
下面我们以一个稍微复杂的电路系统为例,解释由状态变量推导动态系统状态空间方程。
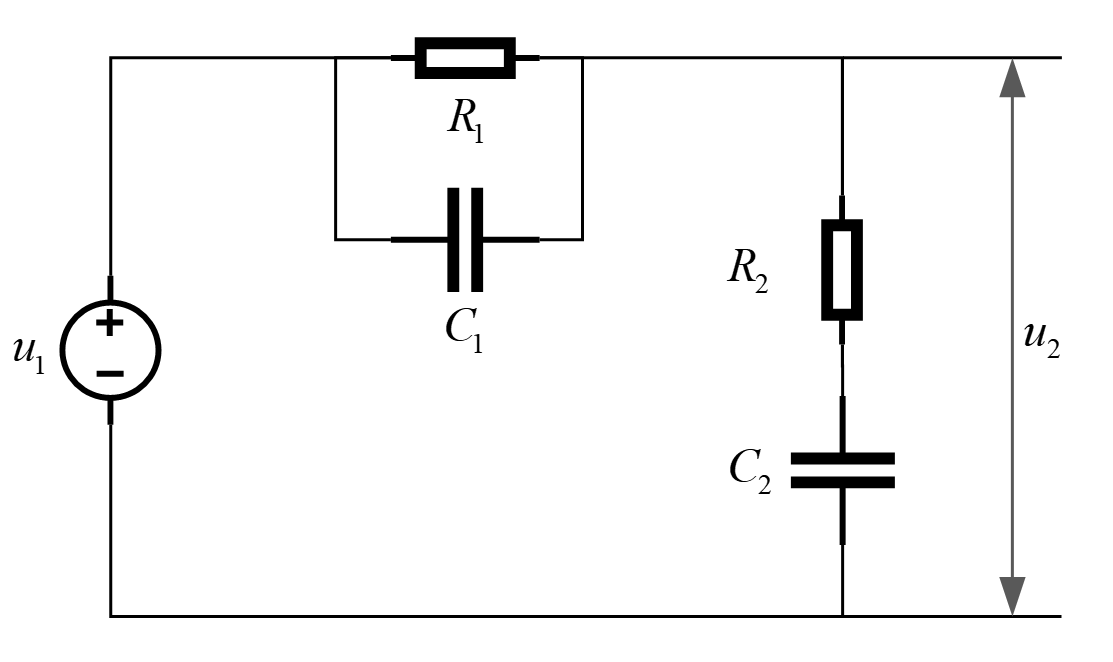
上图所示为一线性时不变电路,设输入为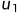 ,输出为
,输出为 ,电阻为
,电阻为 ,电容为
,电容为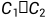 。
。
设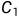 两端电压为
两端电压为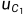 ,
,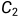 两端电压为
两端电压为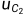 ,则:
,则:
(2.1a)
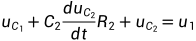
(2.1b)
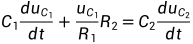
选择状态变量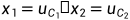 ,由式(2.1a)与式(2.1b)可得:
,由式(2.1a)与式(2.1b)可得:
(2.2a)
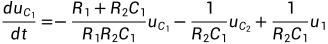
(2.2b)
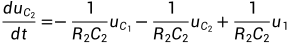
将上式转化为矩阵形式:
(2.3a)
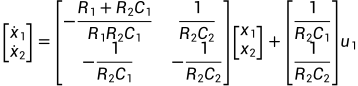
(2.3b)
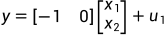
由式(2.3a)、(2.3b)中我们可以看出,在系统状态空间分析中涉及三种类型的变量,即输入变量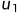 、状态变量
、状态变量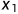 与
与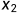 、系统输出量y。
、系统输出量y。
对于更为一般的多输入多输出的系统状态方程,有兴趣的读者可以参考《现代控制工程》,其状态空间表达式为:
(2.4a)
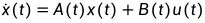
(2.4b)
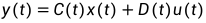
式中: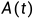 为状态矩阵,
为状态矩阵,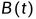 为输入矩阵,
为输入矩阵,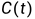 输出矩阵,
输出矩阵,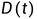 为直接传输矩阵。不难发现,此时式(2.3a)、(2.3b)与式(2.4a)、(2.4b)具有相同的形式,即上述电路为线性定常系统单输入、单输出两个状态变量的状态空间方程实例。
为直接传输矩阵。不难发现,此时式(2.3a)、(2.3b)与式(2.4a)、(2.4b)具有相同的形式,即上述电路为线性定常系统单输入、单输出两个状态变量的状态空间方程实例。
四、如何选择合适的状态变量?
对于一个实际系统来说,状态变量的选取方式并不唯一。比如上文提到的烧水过程,我们可以选择水的压力、温度作为一组状态变量,也可以选择水的压力、密度作为一组状态变量。在Modelica建模过程中,一方面系统会自动选择状态变量,另一方面我们可以手动干预状态变量的选择,合适的状态变量选择有利于系统的求解。
状态变量设置代码方法为stateSelect=StateSelect.xxx。stateSelect是实型变量的一个内置属性,用于控制状态变量的选取,其值有如下5种形式:
StateSelect.always | 总是作为状态变量 |
StateSelect.prefer | 优先选作状态变量 |
StateSelect.default | 缺省值,介于prefer与avoid之间,当以微分变量出现时,可以选作状态变量 |
StateSelect.avoid | 尽量避免作为状态变量 |
StateSelect.never | 从不作为状态变量 |
从always到never,对应变量被选作状态变量的优先级依次降低。即在指标约简之后模型的所有微分变量中,总是选取stateSelect属性值为always的变量作为状态变量,总是不选stateSelect属性值为never的变量作为状态变量,在prefer、default与avoid中,根据需要从prefer到avoid依次选取。下面我们以两个案例说明状态变量选取的方式:
案例1:
Real x(stateSelect = StateSelect.prefer);
Real y;
Equation
x = y;
der(x) + der(y) = 1;在以上示例中,变量y的stateSelect值为缺省值,即为StateSelect.default,而变量x的stateSelect值为StateSelect.prefer。x与y均作为微分变量出现,且存在关于二者的代数方程x =y。方程x = y在指标约简过程中将求一次导数,最终在x与y中只有一个变量作为状态变量。由于x的stateSelect值的优先级高于y,故最终x被选作状态变量。
案例2:
Real x(stateSelect = StateSelect.prefer);
Real y;
Equation
x = y + 0.5;
der(y) = y+1;为了让x作为状态变量,将对下列方程求导,使得x的导数显式出现
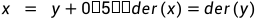
此时y因其导数不再出现,而成为代数变量。
由此可见,将一个代数方程约束的两个变量的stateSelect属性值均设置为always是错误的。此外,default与avoid对代数变量而言等同于never,即使在编译过程中可能引入其导数,也不会将其选作状态变量。
五、建模方法如何影响状态变量?
前面我们已经引入了状态变量、状态空间并且以线性时不变的电路系统为例导出了一般情况下状态空间表达式。下面我们就以一个简单的机械系统为例说明不同的建模方式是如何影响状态变量的选取。
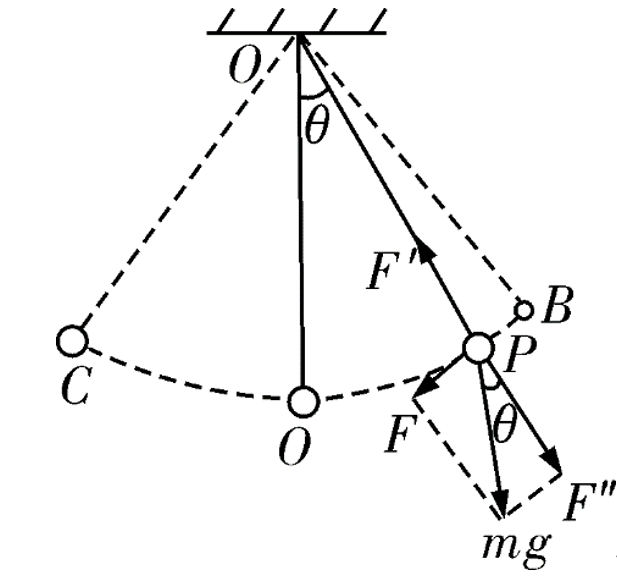
以一个单摆的笛卡尔坐标运动方程为例,其运动学方程可以写出如下形式:
(3.1a)

(3.1b)
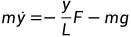
(3.1c)
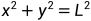
式中m为小球质量,x为水平方向位移,y为竖直方向位移,L为绳长,g为重力加速度,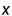 为x的二阶导数,物理含义为小球在水平方向上的加速度,
为x的二阶导数,物理含义为小球在水平方向上的加速度,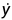 与之同理。
与之同理。
上述式(3.1a)至式(3.1c)形成了一个典型的隐式微分代数方程系统(Implict-DAE),为了正确求解我们需要将上述方程转化为显式常微分方程(Explicit-ODE),步骤如下:
首先我们需要对式(3.1c)进行两次求导,才能显式地暴露变量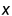 与
与 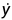 的约束关系,但是与此同时又增加了
的约束关系,但是与此同时又增加了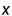 与
与 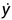 的约束方程:
的约束方程:
(3.2a)

(3.2b)
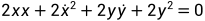
此时为了避免模型求解时雅克比矩阵奇异,状态变量在选择时需要进行动态切换,即当x为0时,我们就必须选取y为状态变量,如果y=0时,则必须选取x为状态变量。
状态变量的动态切换问题是一个组合问题,如果状态变量的排列组合数目很大,从而使雅克比矩阵奇异检测条件非常复杂,此时就会拖慢求解器的求解效率。
应用MWORKS.Sysplorer,我们将上述物理模型利用Modelica语言表达形成如下代码:
model SimplePendulum_XY "单摆实例"
/*参数*/
parameter Modelica.SIunits.Mass m = 0.01 "小球质量";
parameter Modelica.SIunits.Length L = 0.5 "绳长";
/*变量*/
Modelica.SIunits.Distance x "x方向位移";
Modelica.SIunits.Distance y "y方向位移";
Modelica.SIunits.Velocity vx "x方向速度";
Modelica.SIunits.Velocity vy "y方向速度";
Modelica.SIunits.Acceleration ax "x方向加速度";
Modelica.SIunits.Acceleration ay "y方向加速度";
Modelica.SIunits.Force F "绳子拉力";
Modelica.SIunits.Angle theta "转角";
equation
vx = der(x);
vy = der(y);
ax = der(vx);
ay = der(vy);
m * ax = -x / L * F;
m * ay = -y / L * F - m * Modelica.Constants.g_n;
x ^ 2 + y ^ 2 = L ^ 2;
x = L * sin(theta);
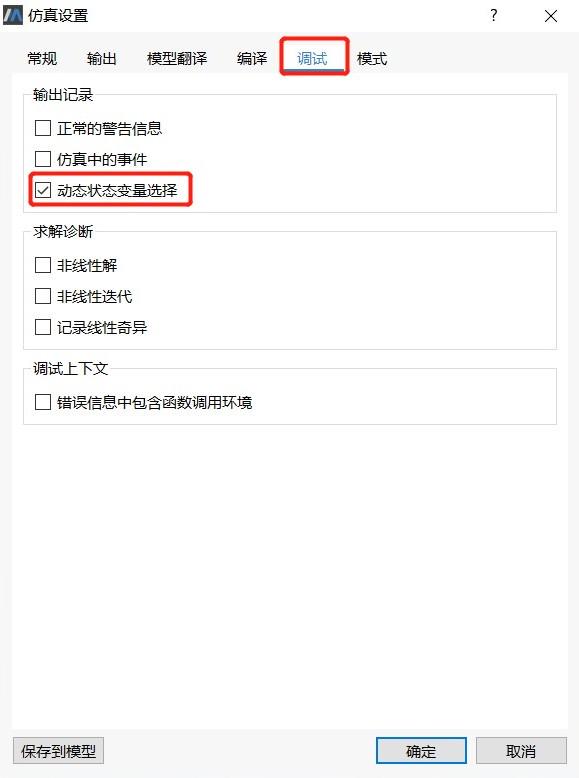
end SimplePendulum_XY;打开“仿真设置-调试-动态状态变量”选择并启动仿真,我们可以在输出栏中发现求解器一直在进行状态变量的切换,仿真10s的时间为0.02s。

假如我们将单摆运动的运动方程做一些改变,引入转角变量 ,重新建立单摆运动方程:
(3.3a)
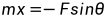
(3.3b)
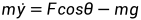
(3.3c)
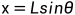
(3.3d)
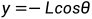
与上述方程同理,对式(3.3c)、式(3.3d)进行求导:
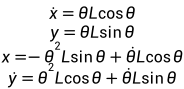
通过引入转角变量,其自动被选为状态变量,原来的x和y不再被选为状态变量,使得系统动态自由度为零,避免由于动态状态变量选择导致的计算效率下降。
应用MWORKS.Sysplorer,我们将上述物理模型利用Modelica语言表达形成如下代码:
model SimplePendulum_theta "单摆实例"
/*参数*/
parameter Modelica.SIunits.Mass m = 0.01 "小球质量";
parameter Modelica.SIunits.Length L = 0.5 "绳长";
/*变量*/
Modelica.SIunits.Distance x "x方向位移";
Modelica.SIunits.Distance y "y方向位移";
Modelica.SIunits.Velocity vx "x方向速度";
Modelica.SIunits.Velocity vy "y方向速度";
Modelica.SIunits.Acceleration ax "x方向加速度";
Modelica.SIunits.Acceleration ay "y方向加速度";
Modelica.SIunits.Force F "绳子拉力";
Modelica.SIunits.Angle theta(start = 1.57) "转角";
equation
vx = der(x);
vy = der(y);
ax = der(vx);
ay = der(vy);
m * ax = -F * sin(theta);
m * ay = F * cos(theta) - m * Modelica.Constants.g_n;
x = L * sin(theta);
y = -L * cos(theta);
end SimplePendulum_theta;输出窗口中,动态状态变量切换已经消失,仿真时间也由0.02s缩短至0.004s,仿真效率提高了5倍!

六、 状态变量初始化
在状态空间表达式中,我们已知了状态变量的导数,为了避免差分法对于小时间步长的局限性,因此利用积分方法对于状态变量进行求解。为了简单的说明求解原理,本文只以显式欧拉法表示,即:
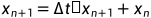
式中: 为第n步计算所得状态变量,
为第n步计算所得状态变量,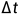 依赖于时间步长和特定积分方法使用的常数。因此状态变量的求解依赖于求解器内置的积分器。
依赖于时间步长和特定积分方法使用的常数。因此状态变量的求解依赖于求解器内置的积分器。
状态变量在积分求解时,一方面依赖于其导数值,另一方面状态变量初始值也同样重要,初始值不同会导致同一Modelica模型的计算结果不同,甚至导致其求解失败。
Modelica语言中初始化方式有两种,分别为初始值初始化与稳态初始化:
a) 初始值初始化:直接为状态变量设定初始值。
parameter Real x0 = 1;
Real x(start = x0, fixed = true);
equation
der(x) = 2*x - 1;上式状态变量x的初始值就即为1。如果用户没有为某个变量设定初始值属性,那么该变量的初始值被缺省地设置为0。
b) 稳态初始化:为变量的导数设定初始值,例如:
Real x;
initial equation
der(x)=0;
equation
der(x)=2 * x-1;根据上述初始条件可以求得x的初始值为:
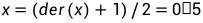
在大型Modelica模型系统状态变量初始化时,使用不同的初始化方式会对计算结果产生不同影响。
对于初始化过程计算速度而言,稳态初始化的计算速度要远远慢于初始值初始化的计算速度。这是因为初始值初始化直接为变量赋值,而稳态初始化过程还需要通过变量的导数以及非线性方程组求解变量的值。
对于初始化后计算结果的稳定性而言,稳态初始化的效果要远好于初始值初始化。这是由于稳态初始化时,状态变量的值根据其导数为零时求得。此时系统中的状态变量更加接近于系统稳定时状态变量的值。
七、总结
本文是一篇Modelica建模秘籍,在最后小编给大家总结了此篇秘籍的口诀心法,请记牢:
1.设置状态变量选取,尽量选择数量级较大且接近同时变化较小的参数。热流系统中,一般情况下我们选择压力、比焓的组合会好于选择温度、密度的状态变量组合;而在机械系统中我们通常选择相对位移(运动副)作为状态变量。
2.减少系统状态变量自由度,避免状态变量的切换。
3.明确状态变量初始值。
4.将非线性量选作状态变量可以有效降低模型系统代数环大小。
状态变量是动态系统建模的重中之重,关系着系统能否正常求解以及求解的效率,小编希望大家看完这篇秘籍,可以成为Modelica建模的高手高高手!
参考材料
1.KatsuhikoOgata,尾形克彦,卢伯英,等.现代控制工程:第四版[M].电子工业出版社,2007.
2.周凡利.工程系统多领域统一模型编译映射与仿真求解研究[D].华中科技大学,2011.
3.丁建完.陈述式仿真模型相容性分析与约简方法研究[D].华中科技大学,2006.