教材为数据库系统概论第五版（王珊）
这一章重点在于各种范式的概念和将低级范式转为高级范式。一定要看多值依赖和4NF（因为这个概念很绕又烦，但是期中期末都考了）。最后计算题就是一定要会：算闭包，求候选码，求最小函数依赖集，看本文的几题例题基本就会了。

6.1 问题的提出

关系数据库逻辑设计

• 针对具体问题，如何构造一个适合于它的数据模式
• 数据库逻辑设计的工具──关系数据库的规范化理论

一、概念回顾

• 关系
• 关系模式
• 关系数据库
• 关系数据库的模式

二、关系模式的形式化定义

关系模式由五部分组成，即它是一个五元组：

R(U, D, DOM, F)

• R： 关系名
• U： 组成该关系的属性名集合
• D： 属性组U中属性所来自的域
• DOM： 属性向域的映象集合
• F： 属性间数据的依赖关系集合

三、什么是数据依赖

1. 完整性约束的表现形式

• 限定属性取值范围：例如学生成绩必须在0-100之间
• 定义属性值间的相互关连（主要体现于值的相等与否），这就是数据依赖，它是数据库模式设计的关键

2. 数据依赖

• 一个关系内部属性与属性之间的约束关系
• 现实世界属性间相互联系的抽象
• 数据内在的性质
• 语义的体现

3. 数据依赖的类型

• 函数依赖（Functional Dependency，简记为FD）
• 多值依赖（Multivalued Dependency，简记为MVD）
• 其他

四、关系模式的简化表示

关系模式R（U, D, DOM, F）简化为一个三元组：

• R（U, F）

当且仅当U上的一个关系r满足F时，r称为关系模式 R（U, F）的一个关系

五、数据依赖对关系模式的影响

例：建立一个描述学校教务的数据库：学生的学号（Sno）、所在系（Sdept），系主任姓名（Mname）、课程名（Cname），成绩（Grade）

单一的关系模式 ：Student <U、F>

U ＝｛ Sno, Sdept, Mname, Cname, Grade ｝

属性组U上的一组函数依赖F：
F ＝｛ Sno → Sdept, Sdept → Mname, (Sno, Cname) → Grade ｝

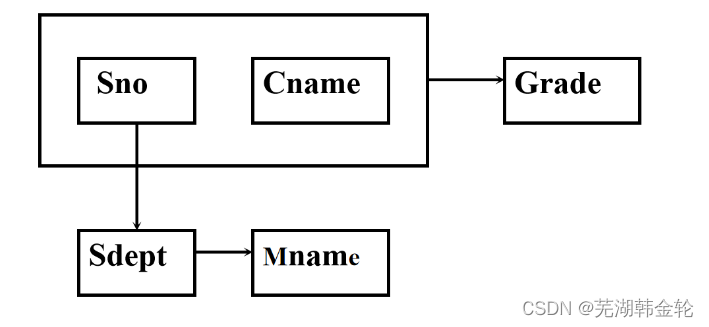
关系模式Student<U, F>中存在的问题

• 数据冗余太大

  • 系主任姓名重复出现，浪费存储空间

• 更新异常（Update Anomalies）

  • 更换系主任？更改系名？

• 插入异常（Insertion Anomalies）

  • 一个系刚成立，尚无学生？

• 删除异常（Deletion Anomalies）

  • 一个系的学生全部毕业了？

结论：

Student关系模式不是一个好的模式。

“好”的模式：不会发生插入异常、删除异常、更新异常，数据冗余应尽可能少

原因：由存在于模式中的某些数据依赖引起的

解决方法：通过分解关系模式来消除其中不合适的数据依赖

6.2 规范化

规范化理论正是用来改造关系模式，通过分解关系模式来消除其中不合适的数据依赖，以解决插入异常、删除异常、更新异常和数据冗余问题。

6.2.1 函数依赖

一、函数依赖

设R(U)是一个属性集U上的关系模式，X和Y是U的子集。

若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等， 而在Y上的属性值不等， 则称 “X函数确定Y” 或 “Y函数依赖于X”，记作X→Y。

说明：

1. 所有关系实例均要满足

2. 语义范畴的概念

3. 数据库设计者可以对现实世界作强制的规定

二、平凡函数依赖与非平凡函数依赖

在关系模式R(U)中，对于U的子集X和Y，

• 如果X→Y，但Y∉X，则称X→Y是非平凡的函数依赖
• 若X→Y，但Y∈X, 则称X→Y是平凡的函数依赖

例：

在关系SC(Sno, Cno, Grade)中，
非平凡函数依赖： (Sno, Cno) → Grade
平凡函数依赖： (Sno, Cno) → Sno ，(Sno, Cno) → Cno

• 若X→Y，则X称为这个函数依赖的决定属性组，也称为决定因素（Determinant）。
• 若X→Y，Y→X，则记作X←→Y。
• 若Y不函数依赖于X，则记作X$\nrightarrow$Y。

三、完全函数依赖与部分函数依赖

在R(U)中，如果X→Y，并且对于X的任何一个真子集X’，都有X’$\nrightarrow $Y,则称Y对X\ast \ast 完全函数依赖\ast \ast ，记作$X\overset{F}{\rightarrow}Y$

若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作$X\stackrel{P}{\to }Y$。

(Sno,Cno)→Grade是完全函数依赖，
(Sno,Cno)→Sdept是部分函数依赖,因为Sno →Sdept成立，且Sno是（Sno，Cno）的真子集

四、传递函数依赖

在R(U)中，如果X→Y，(Y∉X) ,Y$\nrightarrow $XY\to Z，则称Z对X\ast \ast 传递函数依赖\ast \ast 。记为：$X\overset{传递}{\rightarrow}Z$

注意：如果Y→X， 即X←→Y，则Z直接依赖于X。

在关系Std(Sno, Sdept, Mname)中，有：
Sno → Sdept，Sdept → Mname
则Mname传递函数依赖于Sno

6.2.2 码

候选码：

设K为R<U,F>中的属性或属性组合。若$K\stackrel{F}{\to }U$， 则K称为R的侯选码（Candidate Key）。

若候选码多于一个，则选定其中的一个做为主码（Primary Key）。

• 主属性与非主属性
  • 包含在任何一个候选码中的属性称为主属性
  • 不包含在任何码中的属性称为非主属性或非码属性

整个属性组是码，称为全码（All-key）

外码：

关系模式R中属性或属性组X并非R的码，但X是另一个关系模式的码，则称X是R的外部码（Foreign key）也称外码

• 主码与外部码一起提供了表示关系间联系的手段

6.2.3 范式

• 范式是符合某一种级别的关系模式的集合

• 关系数据库中的关系必须满足一定的要求。满足不同程度要求的为不同范式

  范式的种类：

  • 第一范式(1NF)

  • 第二范式(2NF)

  • 第三范式(3NF)

  • BC范式(BCNF)

  • 第四范式(4NF)

  • 第五范式(5NF)

    各种范式之间存在联系：

    

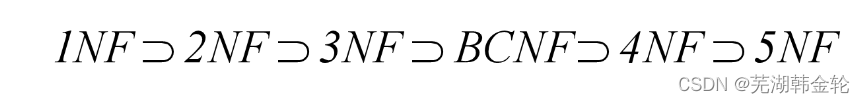
某一关系模式R为第n范式，可简记为R∈nNF

规范化：

一个低一级范式的关系模式，通过模式分解可以转换为若干个高一级范式的关系模式的集合，这种过程就叫规范化

6.2.4 2NF

1NF：

如果一个关系模式R的所有属性都是不可分的基本数据项，则R∈1NF

• 第一范式是对关系模式的最起码的要求。不满足第一范式的数据库模式不能称为关系数据库
• 但是满足第一范式的关系模式并不一定是一个好的关系模式

例：关系模式 S-L-C(Sno, Sdept, Sloc, Cno, Grade)
Sloc为学生住处，假设每个系的学生住在同一个地方

函数依赖包括：

(Sno, Cno) $\stackrel{F}{\to }$ Grade
Sno → Sdept
(Sno, Cno)$\stackrel{P}{\to }$Sdept
Sno → Sloc
(Sno, Cno)$\stackrel{P}{\to }$Sloc
Sdept → Sloc

• S-L-C的码为(Sno, Cno)
• S-L-C满足第一范式
• 非主属性Sdept和Sloc部分函数依赖于码(Sno, Cno)

但S-L-C不是一个好的关系模式

1. 插入异常。插入一个学生信息，但学生还没有选课？
2. 删除异常。学生取消选课，如果所有选课都取消了？
3. 修改复杂。学生转系？住处也要修改
4. 数据冗余度大

原因：Sdept、Sloc部分函数依赖于码。

解决方法：S-L-C分解为两个关系模式，以消除这些部分函数依赖

• SC（Sno， Cno， Grade）
• S-L（Sno， Sdept， Sloc）

不存在非主属性对码的部分依赖

2NF：

若R∈1NF，且每一个非主属性完全函数依赖于码，则R∈2NF。

采用投影分解法将一个1NF的关系分解为多个2NF的关系，可以在一定程度上减轻原1NF关系中存在的插入异常、删除异常、数据冗余度大、修改复杂等问题。但并不能完全消除。

判断一个关系是否属于第二范式：

找出数据表中的所有码；
找出所有主属性和非主属性；
判断所有的非主属性对码的部分函数依赖。

6.2.5 3NF

3NF：

关系模式R<U，F> 中若不存在这样的码X、属性组Y及非主属性Z（Y不包含Z）, 使得X→Y，Y→Z成立，Y$ \nrightarrow $X，则称R<U，F> ∈ 3NF。

若R∈3NF，则每一个非主属性既不部分依赖于码也不传递依赖于码。

若R∈3NF，当且仅当任何时候，每个元组都含有一个主码来识别实体，同时有一组0个或多个相互独立的属性从不同方面描述这个实体。

6.2.6 BCNF

BCNF:

关系模式R<U，F>∈1NF，若X→Y且X不包含Y时X必含有码，则R<U，F> ∈BCNF。

等价于：每一个决定属性因素都包含码

若R∈BCNF

• 所有非主属性对每一个码都是完全函数依赖
• 所有的主属性对每一个不包含它的码，也是完全函数依赖
• 没有任何属性完全函数依赖于非码的任何一组属性

6.2.7 多值依赖

例：学校中某一门课程由多个教师讲授，他们使用相同的一套参考书。每个教员可以讲授多门课程，每种参考书可以供多门课程使用。

非规范化关系：

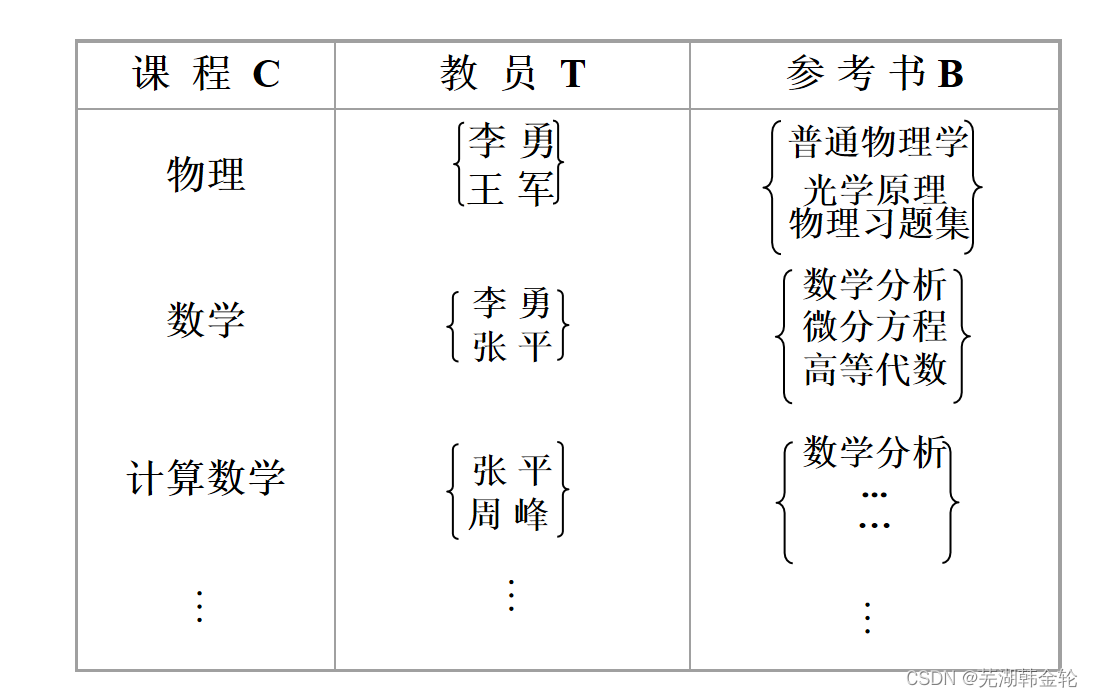
用二维表表示Teaching：

• Teaching∈BCNF
• Teaching具有唯一候选码(C，T，B)， 即全码

Teaching模式中存在的问题：

• 数据冗余度大
• 插入操作复杂。某门课程增加一个教员？需要插入多个元组
• 删除操作复杂。某门课程去掉一本参考书？需要删除多个元组
• 修改操作复杂

多值依赖：(真的难记)

设R(U)是一个属性集U上的一个关系模式， X、 Y和Z是U的子集，并且Z＝U－X－Y。关系模式R(U)中多值依赖 X→→Y成立，当且仅当对R(U)的任一关系r，给定的一对（x，z）值，有一组Y的值，这组值仅仅决定于x值而与z值无关

多值依赖的另一个等价的形式化的定义：

在R（U）的任一关系r中，如果存在元组t，s 使得t[X]=s[X]，那么就必然存在元组 w，v∈ r，（w，v可以与s，t相同），使得w[X]=v[X]=t[X]，而w[Y]=t[Y]，w[Z]=s[Z]，v[Y]=s[Y]，v[Z]=t[Z]（即交换s，t元组的Y值所得的两个新元组必在r中），则Y多值依赖于X，记为X→→Y。 这里，X，Y是U的子集，Z=U-X-Y。

平凡多值依赖和非平凡的多值依赖

• 若X→→Y，而Z＝φ，则称X→→Y为平凡的多值依赖
• 否则称X→→Y为非平凡的多值依赖

多值依赖的性质

（1）多值依赖具有对称性
若X→→Y，则X→→Z，其中Z＝U－X－Y
（2）多值依赖具有传递性
若X→→Y，Y→→Z， 则X→→Z –Y
（3）函数依赖是多值依赖的特殊情况。
若X→Y，则X→→Y。
（4）若X→→Y，X→→Z，则X→→Y∪Z。
（5）若X→→Y，X→→Z，则X→→Y∩Z。
（6）若X→→Y，X→→Z，则X→→Y-Z，X→→Z -Y

多值依赖与函数依赖的区别

(1) 多值依赖的有效性与属性集的范围有关
(2)
若函数依赖X→Y在R（U）上成立，则对于任何Y’⊂Y均有X→Y’ 成立
多值依赖X→→Y若在R(U)上成立，不能断言对于任何Y’⊂Y有X→→Y’ 成立

6.2.8 4NF

4NF:

关系模式R<U，F>∈1NF，如果对于R的每个非平凡多值依赖X→→Y（X不包含Y），X都含有码，则R∈4NF。

如果R ∈ 4NF， 则R ∈ BCNF

• 不允许有非平凡且非函数依赖的多值依赖
• 允许的非平凡多值依赖是函数依赖

6.2.9 规范化小结

• 关系数据库的规范化理论是数据库逻辑设计的工具
• 目的：尽量消除插入、删除异常，修改复杂，数据冗余
• 基本思想：逐步消除数据依赖中不合适的部分
  • 实质：概念的单一化

关系模式规范化的基本步骤

6.3 数据依赖的公理系统

逻辑蕴含：

对于满足一组函数依赖F的关系模式R <U，F>，其任何一个关系r，若函数依赖X→Y都成立,（即r中任意两元组t，s，若t[X]=s[X]，则t[Y]=s[Y]），则称F逻辑蕴含X →Y

Armstrong公理系统

关系模式R <U，F >来说有以下的推理规则：
A1.自反律（Reflexivity）：若Y ⊆ X ⊆ U，则X →Y为F所蕴含。
A2.增广律（Augmentation）：若X→Y为F所蕴含，且Z ⊆ U，则XZ→YZ为F所蕴含。
A3.传递律（Transitivity）：若X→Y及Y→Z为F所蕴含，则X→Z为F所蕴含。

导出规则：

根据A1，A2，A3这三条推理规则可以得到下面三条推理规则：
合并规则：由X→Y，X→Z，有X→YZ。（A2， A3）
伪传递规则：由X→Y，WY→Z，有XW→Z。（A2， A3）
分解规则：由X→Y及 Z⊆Y，有X→Z。（A1， A3）

引理1：

X→A1 A2…Ak成立的充分必要条件是X→Ai成立（i=l，2，…，k）

函数依赖闭包

在关系模式R<U，F>中为F所逻辑蕴含的函数依赖的全体叫作F的闭包，记为F+。

例：

Armstrong公理系统是有效的、完备的

• 有效性：由F出发根据Armstrong公理推导出来的每一个函数依赖一定在F+中；
• 完备性：F+中的每一个函数依赖，必定可以由F出发根据Armstrong公理推导出来

设F为属性集U上的一组函数依赖，X⊆U， X_F+ ={A|X→A能由F 根据Armstrong公理导出}，X_F+称为属性集X关于函数依赖集F的闭包

求闭包的算法：

例：背下这些详细步骤

候选码求解方法

对关系模式R<U,F>，选取可能是候选码的属性集，求其函数依赖闭包，如果属性集的函数依赖闭包=U，则该属性集为候选码
三类属性
L类：仅出现在F的函数依赖左边
R类：仅出现在F的函数依赖右边
N类：没有出现在F的函数依赖中

定理1：L类属性必为任一候选码的成员
定理2：R类属性不在任何候选码中
定理3：N类属性必包含在任何候选码中

最小函数依赖集

定义：如果函数依赖集F满足以下条件，则称F为一个极小函数依赖集。也称为最小依赖集或最小覆盖。
(1)F中任一函数依赖的右部仅含有一个属性。
(2)F中不存在这样的函数依赖X→A，使得F与F-{X→A}等价。
(3)F中不存在这样的函数依赖X→A，X有真子集Z使得F-{X→A}U{Z→A}与F等价。

最小依赖集通用算法：

① 用分解的法则，使F中的任何一个函数依赖的右部仅含有一个属性；
② 去掉多余的函数依赖：从第一个函数依赖X→Y开始将其从F中去掉，然后在剩下的函数依赖中求X的闭包X+，看X+是否包含Y，若是，则去掉X→Y；否则不能去掉，依次做下去。直到找不到冗余的函数依赖；
③ 去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖。例如XY→A，若要判Y为多余的，则以X→A代替XY→A是否等价？若A属于(X)+，则Y是多余属性，可以去掉。（以上步骤中，求出关系依赖集F,此时，在F的基础上，求出X或者Y的闭包，是否包含A）

注意：第三步求闭包使用的依赖集是第二步求出时的。

例：关系模式R(U，F)中，U=ABCDEG，F={B->D，DG->C,BD->E,AG->B,ADG->BC}；求F的最小函数依赖集

最后建议这章还是找点题目来做，也是有一定占比的

随便找的几篇：

http://t.csdn.cn/aFuG9

http://t.csdn.cn/cUnNC考试更会考这种贴近生活的例子