函数概念

函数我们可以简单的理解为一个自变量只对应一个函数值,如图:
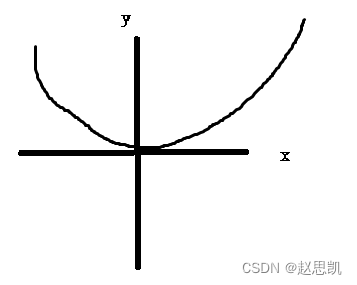
如图所示的图像,我们可以把其理解为函数,那非函数呢?
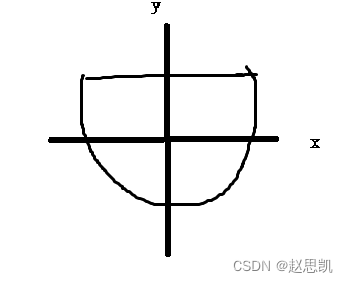
这个就叫做非函数,因为我们的一个自变量对应了两个函数值。
函数的两要素:对应法则和定义域。
只要有了对应法则和定义域,我们也就能够得到函数的值域了。
符号函数:

符号函数就是特殊的分段函数,当自变量的值小于0时,返回-1,当自变量的值等于0时,返回0,当自变量的值大于0时,返回1.
取整函数:

例如,[3.2]=3,[-4.5]=-5.
复合函数:

如何满足复合函数?
答:对于两个函数y=f(u)和函数u=g(x)来说,假如我们要构建一个复合函数,内层函数是函数u,外层函数是y,我们只需要满足外层函数的定义域与内层函数的定义域的交集不为空即可。
这个函数的定义域是x满足内层函数的定义域,g(x)满足外层函数的定义域。
不是对于任何两个函数都有复合函数,例如:
答:![]()
函数f(u)的定义域为(0,正无穷),函数g(x)的值域是[-2,0],两个区域没有交集,所以没有复合函数。
反函数:

我们可以这样理解:
什么是函数呢?
答: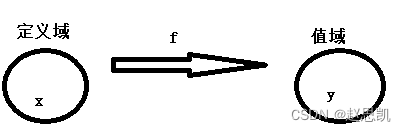
通过自变量x,通过法则f的映射,有唯一确定的值与其对应,这就叫做函数。
但是,一个函数值却可以对应多个自变量,这就叫做函数的定义。
我们倒过来:
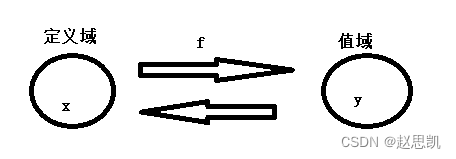
对于一个函数,假如满足一个函数值可以对应一个自变量,那这个函数就一定有反函数。
例如:
我们画出y=x^3的图像:
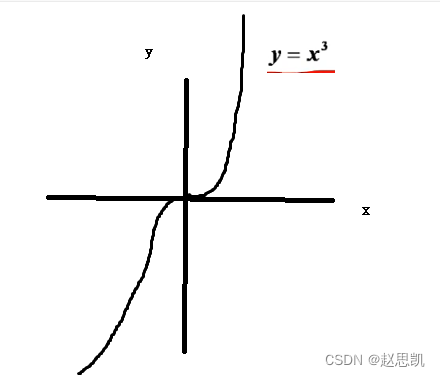
我们发现,这个函数一个函数值y,只对应一个自变量,所以他有反函数。
例如: ![]()
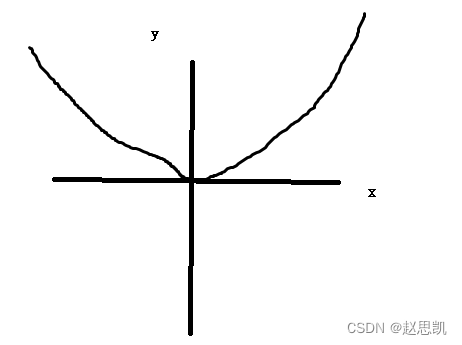
对于这个函数,一个函数值对应有两个自变量,这个函数就没有反函数。
单调函数一定有反函数。
对于单调函数,函数是连续增加或者连续减小的,对于一个函数值,只有唯一的自变量与其对应。
但是假如一个函数有反函数,他却不一定单调。

例如如图所示的函数图像,我们一个函数值只有唯一的自变量与其对应,所以这个函数有反函数,但是这个函数却不是单调的。
所以一个函数单调是这个函数有反函数的充分非必要条件。
函数有反函数的充要条件是一个函数值只映射一个自变量。
反函数的特点:

我们如何理解:

所以对于一个函数,可以有两种不同的反函数写法。
反函数题目:
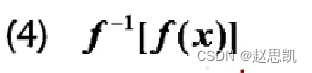
这道题目的结果是多少?
我们画图进行解释:
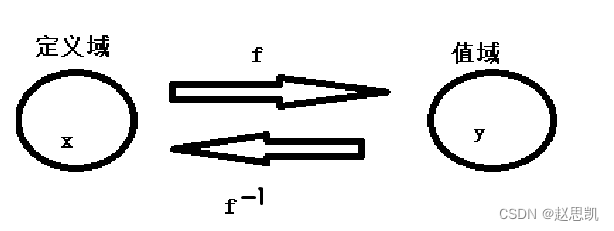
f(x)的本质是通过映射关系f找到对应的函数值y,反函数则是通过映射关系找到对应的自变量x,于是我们最终的结果就是x
求函数的反函数:
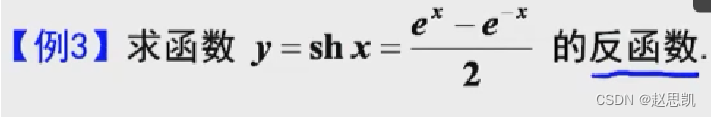

这就是求反函数的步骤。
初等函数:


例如:
这个就是初等函数。
单调性:

奇偶性:

奇函数:

偶函数:
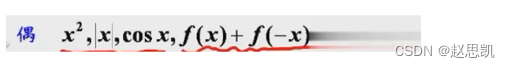
奇偶函数的性质:


例题:
![]()

周期函数:

有界函数:

这里的M代表的是边界,对于任意的自变量,都满足f(x)的边界在M之间的话,就称f(x)在x上是有界函数。
无界和有界的是完全相反。
下界:|f(x)|>=M。
上界: |f(x)|<=M.
一个函数是有界函数能推出这个函数既有上界又有下界,一个函数既有上界又有下届并不能够推出这个函数是有界函数。
举例:

这个函数是有界函数吗?为什么
这个函数在[0,1]上是有界的,在[1,2]上是无界的,所以是无界函数。
例题:
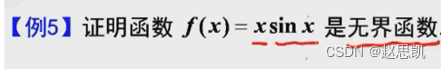

例题2:
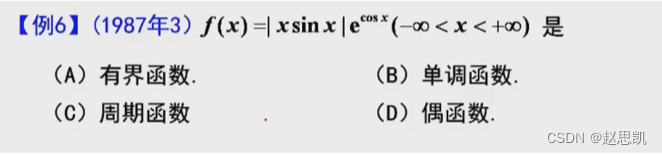
A:
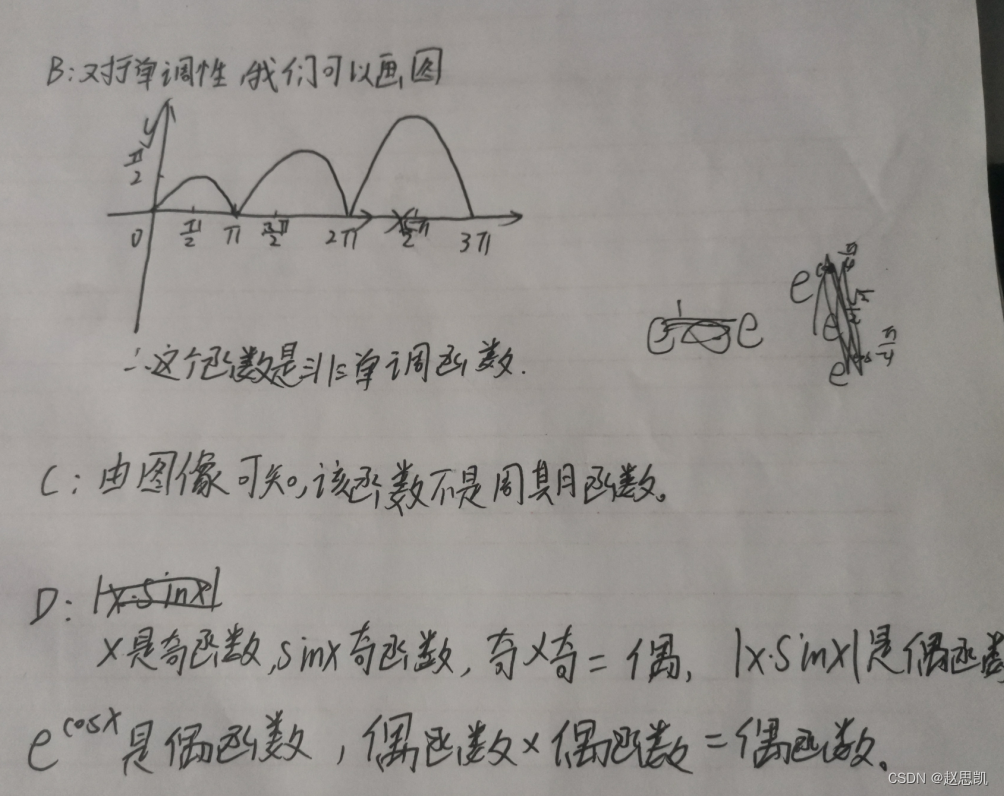
例题:

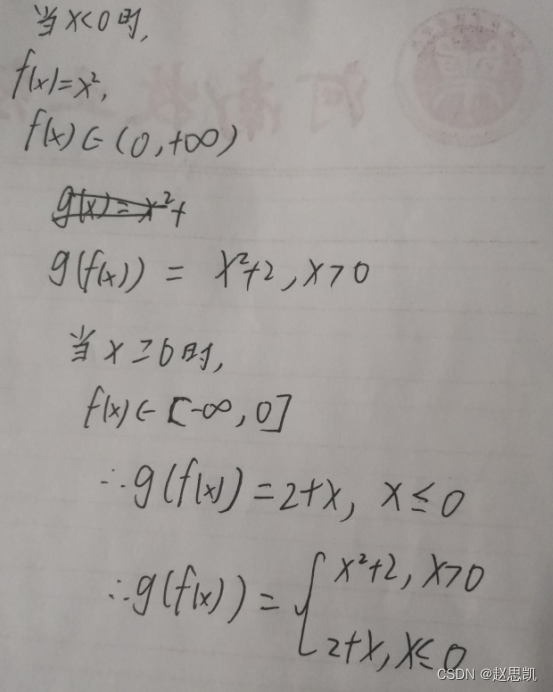
例题:
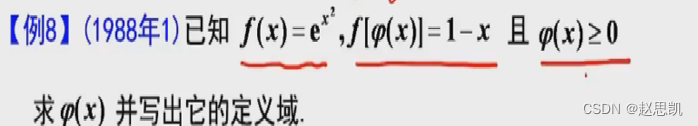






![[C++]string类模拟实现](https://img-blog.csdnimg.cn/c60fc66ba14e48b3837bd944fb19fccd.png)