基于莱维飞行扰动策略的麻雀搜索算法

摘要：为了解决麻雀搜索算法存在迭代后期搜索多样性不足、容易陷入局部最优等问题,提出了一种基于莱维飞行扰动策略的改进麻雀搜索算法。首先借鉴Sin混沌搜索机制,改进种群初始化策略。然后在麻雀种群觅食搜索过程中引入莱维飞行扰动机制,牵引种群移动适当的步长,增加空间搜索的多样性。

1.麻雀优化算法

基础麻雀算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/108830958

2. 改进麻雀算法

2.1 莱维飞行搜索机制

随着仿生学的不断发展, 模拟布谷鸟巢寄生行为的 CS 算法应运而生。生物学的研究表 明: 布谷鸟利用餒育寄生的方式繁衍后代, 表现为产卵寄生于其他宿主鸟巢并在其他宿主鸟 的帮助下孵化和育雉的一种生物行为, 其繁殖行为关于选巢位置的变化正好体现出莱维飞行 的搜索特性。

CS 算法是将布谷鸟寻窝产卵和莱维飞行的搜索机制形成搜索策略。该算法约定以下 3 条 规则：1）每只布谷鸟每次只产卵一个, 并随机选择寄生巢来卿化；2）在随机选择的一组寄生 巢中, 将最好的寄生巢保留到下一代；3）约定寄生巢的数量, 且宿主鸟按一定的概率发现寄 生卵。在这 3 条规则的约束下, 宿主鸟可以将产卵抛出, 或放弃该鸟巢以建新巢。Levy $(\lambda )$ 是 一个随机搜索路径, 其随机步长表现为一个 Levy 分布, 具体计算公式为
$$Levy\sim u=t^{-\lambda },1<\lambda ⩽3\text{\hspace{1em}(6)}$$
布谷鸟通过莱维飞行寻窝搜索的路径和位置更新公式为
$$x_i^{t+1}=x_i^t+\delta \oplus \mathrm{Levy}(\lambda )\text{\hspace{1em}(7)}$$
式中: $x_i^t$ 表示第 $i$ 个鸟窝在第 $t$ 代的位置; $\delta$ 表示步长大小, $\delta >0$, 通常设置为 $\delta =1;\oplus$ 表 示点对点乘法。

2.2 莱维飞行扰动策略

在 CS 算法中, 采用莱维飞行可以产生变化多样的随机步长。在搜索过程中, 如果步长较 大, 全局搜索范围较广, 则搜索精度会降低, 易产生不稳定的震荡现状; 如果步长较小, 局部 寻优能力增强, 则搜索精度会显著增强。因此, 采用莱维飞行产生的步长具有遍历性和随机 性, 但自适应能力不够。SSA 为了弥补这一不足, 利用发现者-跟随者-警戒者的模型机制, 提 高了全局搜索能力和局部求解精度。
本文受 $\mathrm{CS}$ 算法启发构建莱维飞行步长扰动方法, 扰动步长 $S_p$ 的计算公式如式 (8) (11) 所示:
$$\begin{array}{rlr}{s}_i& =\frac{u}{|v{|}^{1/\beta }}& (8)\\ u& \sim N\left(0,{\delta }_u^2\right),v\sim N\left(0,{\delta }_v^2\right)& (9)\\ {\delta }_u& ={\left\{\frac{\Gamma (1+\beta )\sin (\pi \beta /2)}{\Gamma [(1+\beta )/2]\beta 2^{(\beta -1)/2}}\right\}}^{1/\beta },{\delta }_v=1& (10)\\ S_p& =\tau s_i{x}_{\text{best }}^j& (11)\end{array}$$
式中: i ∈ { 1 , 2 , ⋯   , n } , j ∈ { 1 , 2 , ⋯   , D } , u i \in\{1,2, \cdots, n\}, j \in\{1,2, \cdots, D\}, u i∈{1,2,⋯,n},j∈{1,2,⋯,D},u 和 $v$ 属于正态分布, $\beta =1.5$ 。麻雀搜索位置步长 扰动定义为
$$v_{i,j}=v_{i,j}{S}_p\text{\hspace{1em}(12)}$$

2.3 初始化混沌搜索机制

本文对传统的 SSA 进行了初始化搜索策略的改进。根据 Sin 混沌模型初始化种群分布, 增加种群搜索的多样性, 则产生不同数值的混沌序列可以定义为
$$x_{n+1}=\sin \left(\frac{2}{x_n}\right)\text{\hspace{1em}(13)}$$
式中: $x_n\in [-1,1]$ 且 $x_n\ne 0,n=0,1,\cdots ,N$ 。

LSSA 的伪代码算法步骤如下:
步骤 1 参数设置
设置麻雀种群规模数 $n$ 、麻雀发现者数量 $P_d$ 、警戒者数量 $S_d$ 、寻食步数计数器 $t$ 为 0 、最 大寻食迭代次数为 $T_{\max }$ 。
步骤 2 初始化种群
在搜索区域内按式 (13) 产生 $n$ 个向量 $X_i(i=1,2,\cdots ,n)$, 计算适应度值并记录适应度 值的最佳和最差个体位置。
步骤 3 发现者搜索
根据式 (3) 搜索更新发现者位置。
步骤 4 加入者搜索
根据式 (4) 搜索更新加入者位置。
步骤 5 檠戒者搜索
根据式 (5) 搜索更新警戒者位置。

步骤 6 根据适应度值更新位置
比较 $y_{\min }$ 与 $G_{\min }$, 若 $y_{\min }⩽G_{\min }$, 则令 $G_{\min }=y_{\min },X_g(t)=X_g^{\prime }(t)$, 记录当前所有麻 雀找到的最优位置, 即全局最优解 $s^{\ast }$ 。
步骤 7 莱维飞行机制
随机生成一个数 $r$, 设置概率 $p_i$, 如果 $r<p_i$, 则根据式 (12) 进行莱维飞行搜索。
步骤 8 更新迭代次数, 若满足当前迭代次数 $t>T_{\max }$, 则搜索停止, 输出全局最优位置 $X_g$ 和求解结果 $f_{\mathrm{opt}}\left(X_g\right)$; 否则转步骤 3 继续执行。

3.实验结果

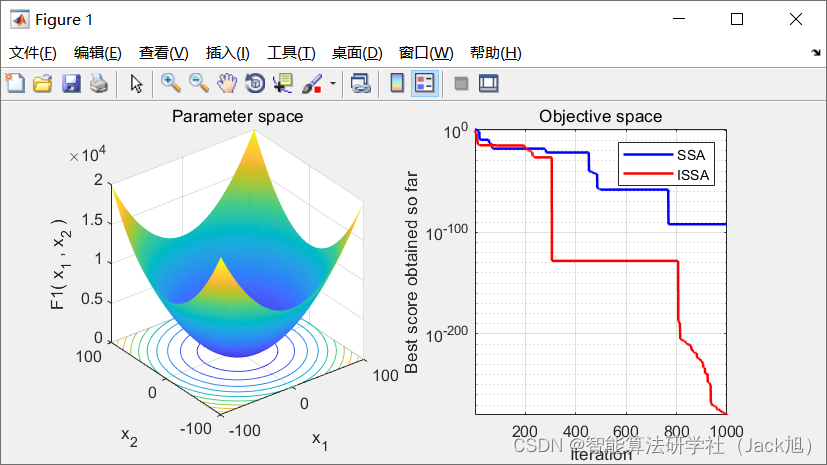
4.参考文献

[1]马卫,朱娴.基于莱维飞行扰动策略的麻雀搜索算法[J].应用科学学报,2022,40(01):116-130.

5.Matlab代码

6.Python代码