实例9：四足机器人正向运动学单腿可视化

实验目的

1. 通过动手实践，搭建mini pupper四足机器人的腿部，掌握机器人单腿结构。
2. 通过理论学习，熟悉几何法、旋转矩阵法在运动学正解（FK）中的用处。
3. 通过编程实践，熟悉可视化简化机器人单腿的方法。

实验要求

通过Python编程，在简化的mini pupper平面二连杆模型内，让用户输入关节角，根据关节角及关节的基本信息，计算出每个关节相对于基坐标系的坐标，并将其可视化输出。

实验知识

1.什么是正向运动学 Forward Kinematics ？

在mini pupper的实际运动操作中，需要考虑计算小腿末端相对身体基座标系位置和姿态关系的静态几何问题。简单来说，就是给定一组关节角的值，计算小腿末端坐标系相对于基坐标系的位姿。
正向运动学探究的问题可以看做由关节空间Joint Space $（{\theta }_1,{\theta }_2,\cdot \cdot \cdot \cdot ,{\theta }_n）$描述到 笛卡尔空间Cartesian Space ${（}^{World}P）$ 描述的位置表示。
探究这种位置的表示关系就是正向运动学，对于机器人来说，就是以操作臂的关节变量为自变量，描述操作臂末端执行器的位姿与基坐标系之间的函数关系。

2.怎么描述机器人的一条腿？

既然要考虑计算mini pupper实际运动中小腿末端相对身体基座标系位置和姿态关系的计算，就应该有对应的定性和定量的描述及表示来使得计算能够实现。
在机器人学中，操作臂由连杆link组成，将连杆视作刚体，相邻连杆由关节joint连接，关节可以相对 转动（revolute） 或者 移动（prismatic），转动的轴被称为Axis。
操作臂的这种描述对应到人体上，可以看作简化的人类的手臂，“大臂”就是一个连杆，通过“肘关节”这个关节和另一个连杆“小臂”相连，mini pupper也是相同的道理。

关节的转动和移动引出了两个数学量，对于转动关节，相邻杆件的相对角度变化被称为关节角，而对于移动关节，相邻杆件之间的相对位移变化被称为关节偏移量。

对于操作臂来说，自由度的数量是具有独立的位置变量的数目，常见的工业机器人大都是开式的运动链，每个关节位置由唯一变量来定义，因此关节的数目常常等于自由度的数量。

操作臂的末端被称为末端执行器，比如夹具、焊枪等，通常用设置在末端执行器上的工具坐标系Frame_Tool与操作臂的固定底座的参考基坐标系Frame_Base的相对关系，来描述操作臂的位置与姿态。

3.怎么描述腿间部件的关系？

为了描述相邻连杆之间的关系，引入了4个变量对连杆的空间关系进行描述。

名称	符号	含义	注释
连杆长度	$a_{i-1}$	两个相邻关节轴之间公垂线的长度	连杆长度是沿着${\hat{X}}_{i-1}$方向，${\hat{Z}}_{i-1}$和${\hat{Z}}_i$之间公垂线的长度。因为$a_{i-1}$是距离，所以始终有$a_{i-1}\ge 0$。
连杆扭转角	${\alpha }_{i-1}$	沿着$a_{i-1}$方向的投影平面中两关节轴线的夹角	连杆扭转角是沿着${\hat{X}}_{i-1}$方向看去所形成的的二维平面内${\hat{Z}}_{i-1}$和${\hat{Z}}_i$的夹角，按照右手法从${\hat{Z}}_{i-1}$扭向${\hat{Z}}_i$取正负。
连杆偏距	$d_i$	沿两个相邻连杆公共轴线方向的距离。	沿着${\hat{Z}}_i$方向看去，对于${\hat{X}}_{i-1}$与${\hat{Z}}_i$所在直线的相交点和${\hat{X}}_i$与${\hat{Z}}_i$所在直线的相交点，这两个相交点的距离。
关节角	${\theta }_i$	两相邻连杆绕公共轴线旋转的角度。	沿着${\hat{Z}}_i$方向看，二维平面内${\hat{X}}_{i-1}$和${\hat{X}}_i$的夹角，方向为${\hat{X}}_{i-1}$扭向${\hat{X}}_i$。

连杆扭转角和连杆长度定义了同一杆件的两个关节轴之间的关系，关节角和连杆偏距定义了连杆是如何连接的。
上表注释中提及的${\hat{X}}_i$、${\hat{Y}}_i$、${\hat{Z}}_i$将在后文中结合连杆坐标系提及，可结合理解。

4.Denavit-Hartenberg表达法

简称为DH表达法，版本为Craig version，DH法是用四个连杆参数来描述机构运动关系的规则，两个参数用于描述连杆本身，另外两个参数用于描述连杆之间的连接关系。
这四个参数即是之前所提到的连杆扭转角${\alpha }_{i-1}$、连杆长度$a_{i-1}$、关节角${\theta }_i$、连杆偏距$d_i$。
通常来说，对于转动关节，关节变量为关节角${\theta }_i$，对于移动关节，关节变量为连杆偏距$d_i$。
对于这类关节，除了关节变量外的其他的三个连杆参数都是固定不变的硬件属性参数。

5.连杆坐标系

为了描述连杆间的关系，坐标系被引入，因此需要在每个连杆上建立连杆坐标系，对于连杆$i-1$，其上有连杆坐标系 { i − 1 } \{i-1\} {i−1}，在Craig改良DH法中，连杆坐标系的原点通常被规定在在关节轴$Axi{s}_{(i-1)}$上。
按照这种坐标系的规定，固定连杆坐标系的各正交轴如下：

轴或点	定义
原点	公垂线$a_i$与关节轴$Axi{s}_i$的交点
${\hat{Z}}_i$	与关节轴$Axi{s}_i$重合
${\hat{X}}_i$	沿着 公垂线$a_i$由关节$join{t}_i$指向关节$join{t}_{i+1}$方向。当公垂线$a_i=0$时，${\hat{X}}_i$垂直于 ${\hat{Z}}_i$与 ${\hat{Z}}_{i+1}$形成的平面，可以有两个方向，根据方便选用
${\hat{Y}}_i$	根据右手定则确定，已知拇指为 ${\hat{X}}_i$，食指为${\hat{Y}}_i$ ，已知中指为${\hat{Z}}_i$

连杆坐标系中的特殊存在

首端连杆

首端连杆被称为地杆，机器人的固定基座上的坐标系 { 0 } \{0\} {0}常被用作参考坐标系。${\hat{Z}}_0$方向和${\hat{Z}}_1$相同，并当坐标系 { 1 } \{1\} {1}的关节变量${\theta }_i$或$d_i$为0时，使坐标系 { 0 } \{0\} {0}和坐标系 { 1 } \{1\} {1}重合，以简化计算。

$$\text{转动关节Revolute joint}{\alpha }_0=0a_0=0d_1=0{\theta }_1=?(当为0时Frame重合)$$
$$\text{移动关节Prismatic joint}{\alpha }_0=0a_0=0{\theta }_1=0d_1=？(当为0时Frame重合)$$

末端连杆

末端杆没有下一根杆件，因此要和上一根杆件找关联。
对于转动关节，${\hat{X}}_n$方向和${\hat{X}}_{n-1}$相同，再选取设置原点使得$d_n=0$
对于移动关节，选取设置${\hat{X}}_n$方向使得${\theta }_n=0$，当$d_n=0$时，原点位于关节轴$n$和${\hat{X}}_{n-1}$交点处

学习完连杆坐标系中，连杆参数可以更简单地理解:

名称	符号	含义
连杆扭转角	${\alpha }_{i-1}$	连杆扭转角是绕${\hat{X}}_{i-1}$轴，${\hat{Z}}_{i-1}$旋转到${\hat{Z}}_i$的夹角
连杆长度	$a_{i-1}$	连杆长度是沿着${\hat{X}}_{i-1}$轴，${\hat{Z}}_{i-1}$移动到${\hat{Z}}_i$的公垂线的长度
关节角	${\theta }_i$	绕${\hat{Z}}_i$轴，${\hat{X}}_{i-1}$旋转到${\hat{X}}_i$的夹角
连杆偏距	$d_i$	沿着${\hat{Z}}_i$轴，${\hat{X}}_{i-1}$移动到${\hat{X}}_i$的距离

建立连杆坐标系和DH表

1. 找出关节轴
   分析运动状态，找出关节平移或转动的轴向（joint axes）
2. 找出${\hat{Z}}_i$
   ${\hat{Z}}_i$的正方向为转动或移动的轴axis方向
3. 找出${\hat{X}}_i$
   ${\hat{X}}_i$的正方向是两个关节轴之间公垂线上，指向下一个关节轴的方向
   （$a_i=0$时，即当两关节轴相交时，$X$和$Z_i$和$Z_{i+1}$的方向垂直，此时方向怎么方便怎么来）
4. 确定原点
   原点即为${\hat{Z}}_i$与${\hat{X}}_i$的交点
5. 找出${\hat{Y}}_i$
   根据右手定则确定，拇指为 ${\hat{X}}_i$，食指为${\hat{Y}}_i$ ，中指为${\hat{Z}}_i$
6. 处理首端连杆
   并当$Fram{e}_1$的关节变量${\theta }_i$或$d_i$为0时，使$Fram{e}_0$和$Fram{e}_1$重合，以简化计算。
7. 处理末端连杆
   尽量使得连杆参数为0以简化计算

根据以上几步处理的结果，可以获取DH参数表

DH参数表是Frame之间的关系，每个i代表一对轴之间的关系
表中的1为基坐标系$Fram{e}_0$与第一个轴坐标系$Fram{e}_1$的关系
表中的3为末端连杆与最后一个可（转、平移）的轴的关系

i	${\alpha }_{i-1}$	$a_{i-1}$	${\theta }_i$	$d_i$
1	0	0	${\theta }_1$	0
2	0	$L_1$	${\theta }_2$	0
3	0	$L_2$	${\theta }_3$	0

6.连杆坐标系之间的转化

对于$Fram{e}_{i-1}$，要从$Axi{s}_{i-1}$到$Axi{s}_i$。
首先，完成从${\hat{Z}}_{i-1}$到${\hat{Z}}_i$的旋转${\alpha }_{i-1}$和平移$a_{i-1}$距离。

然后，将旋转和平移后的$Axi{s}_{i-1}$旋转${\theta }_i$，并沿着${\hat{Z}}_i$方向平移$d_i$距离。
总计进行四次操作，最终可得
$${}^{i-1}P{=}_i^{i-1}{T}^{i}P$$
${}_i^{i-1}T$中合并了这四次操作，得出该变换矩阵：
$${}_i^{i-1}T=\left[\begin{array}{cccc}Cos{\theta }_i& -Sin{\theta }_i& 0& a_{i-1}\\ Sin{\theta }_{i}Cos{\alpha }_{i-1}& Cos{\theta }_{i}Cos{\alpha }_{i-1}& -Sin{\alpha }_{i-1}& -Sin{\alpha }_{i-1}{d}_i\\ Sin{\theta }_{i}Sin{\alpha }_{i-1}& Cos{\theta }_{i}Sin{\alpha }_{i-1}& Cos{\alpha }_{i-1}& Cos{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]$$
多次使用该变换矩阵可以得出不相邻的关节之间的转化关系

7.mini pupper的简化运动学结构

mini pupper的单条腿部可简化视作典型的三连杆非平面操作臂，三自由度的设计使得它理论上能够到达空间限位范围内的任意位置。
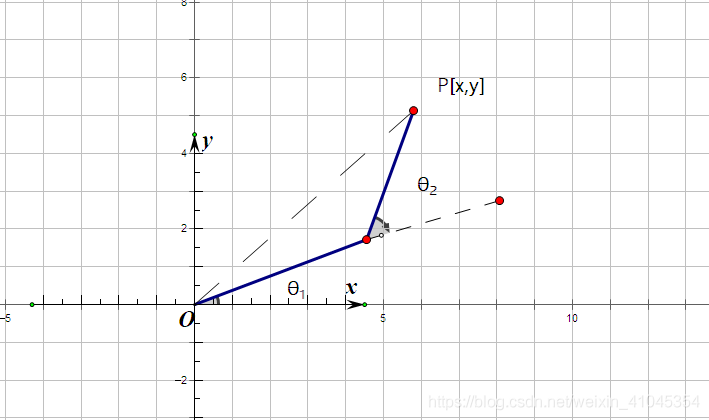
当我们进一步简化，不考虑横向髋关节运动时，mini pupper的腿部可以简化为平面二连杆机构RR模型，使用几何解法即可在已知${\theta }_1$和${\theta }_2$的情况下求得${}^{0}P$的坐标，完成运动学正解。
对于大臂与小臂相交处$Q$：
$$x_q=l_{1}Cos{\theta }_1$$
$$y_q=l_{1}Sin{\theta }_1$$

对于小臂末端点：
$$x_p=l_{1}Cos{\theta }_1+l_{2}Cos({\theta }_1+{\theta }_2)$$
$$y_p=l_{1}Sin{\theta }_1+l_{2}Sin({\theta }_1+{\theta }_2)$$

图片：平面二连杆机构RR模型

实验步骤

1. 编写Python代码 rr_manipulator.py

#!/usr/bin/python
# coding:utf-8
# rr_manipulator.py
# mini pupper的简化单腿，可视作同一平面的RR类机械臂，可视化该机械臂，由给定角度计算末端点位置
import matplotlib.pyplot as plt  # 引入matplotlib
import numpy as np  # 引入numpy
from math import radians, sin, cos


# 几何法：关节角转端点坐标
def theta_2_position_rr(l1, l2, theta1, theta2):
    """
    运动学正解 将输入的关节角转化为对应的端点坐标
    :param l1: 大臂长
    :param l2: 小臂长
    :param theta1: 大臂关节角
    :param theta2: 小臂关节角
    :return: 端点1坐标 端点2坐标
    """
    point_1 = [l1*cos(radians(theta1)), l1*sin(radians(theta1))]
    point_2 = [l1*cos(radians(theta1))+l2*cos(radians(theta1+theta2)),
               l1*sin(radians(theta1))+l2*sin(radians(theta1+theta2))]
    print(point_1)
    print(point_2)
    return point_1, point_2

def preprocess_drawing_data(points):
    """
    处理点坐标数据转化为matplotlib适应的绘图格式
    :param points: 点数据
    :return: 绘图数据x坐标list和对应的y坐标list
    """
    xs = [0]
    ys = [0]
    xs.append(points[0][0])
    xs.append(points[1][0])
    ys.append(points[0][1])
    ys.append(points[1][1])
    return xs, ys


# 关节信息
# 大臂长度：5 cm 小臂长度：6 cm
link_length = [5, 6]  # in cm

# 关节角初始化
joints_angle_origin = [30, 30]
joints_angle = [0, 0]
print("关节角初始状态 theta1=%d°， theta2=%d°" % (joints_angle_origin[0], joints_angle_origin[1]))

# 输入连杆参数：各关节角
for i in range(1, 3):
    joints_angle[i-1] = int(input("请输入腿部舵机[%d]要转动的的角度：" % i))
    print("腿部舵机[{0}]将转动{1}°".format(i, joints_angle[i-1]))

# 计算并预处理绘图数据
points_origin = theta_2_position_rr(link_length[0], link_length[1], joints_angle_origin[0], joints_angle_origin[1])
points_after = theta_2_position_rr(link_length[0], link_length[1], joints_angle[0], joints_angle[1])
data_origin = preprocess_drawing_data(points_origin)
data_after = preprocess_drawing_data(points_after)

# 绘图
fig, ax = plt.subplots()  # 建立图像
plt.plot(data_origin[0], data_origin[1], color='black', label='original')
plt.scatter(data_origin[0], data_origin[1], color='black')
plt.plot(data_after[0], data_after[1], color='red', label='after')
plt.scatter(data_after[0], data_after[1], color='blue')
ax.set(xlabel='X', ylabel='Y', title='mini pupper FK RR model')
ax.grid()
plt.legend()
plt.show()

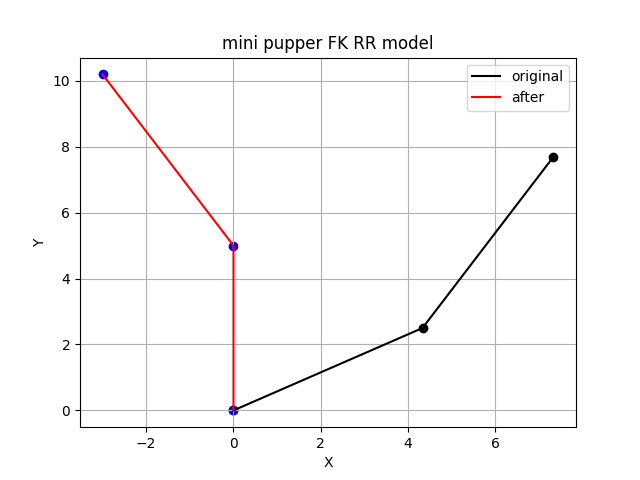
2. 运行程序，观察效果

在rr_manipulator.py的目录下执行以下命令：

sudo python rr_manipulator.py

此时应观察到根据关节角计算出的可视化坐标。

实验总结

经过本知识点的学习和实验操作，你应该能达到以下水平：

知识点	内容	了解	熟悉	掌握
硬件	mini pupper单腿结构的搭建			✔
运动学	平面RR类型机械臂的运动学正解			✔
运动学	非平面RRR类型机械臂	✔
运动学	几何法完成运动学正解		✔
运动学	运动学正解基础知识		✔
可视化	Python可视化运动学	✔

版权信息：教材尚未完善，此处预留版权信息处理方式
mini pupper相关内容可访问：https://github.com/mangdangroboticsclub