14、KL散度

news2024/9/30 15:22:44

KL 散度，是一个用来衡量两个概率分布的相似性的一个度量指标。

现实世界里的任何观察都可以看成表示成信息和数据，一般来说，我们无法获取数据的总体，我们只能拿到数据的部分样本，根据数据的部分样本，我们会对数据的整体做一个近似的估计，而数据整体本身有一个真实的分布（我们可能永远无法知道）。

那么近似估计的概率分布和数据整体真实的概率分布的相似度，或者说差异程度，可以用 KL 散度来表示。

KL 散度，最早是从信息论里演化而来的。所以在介绍 KL 散度之前，先介绍一下信息论里有关熵的概念。

熵

信息论中，某个信息 $\large x_{i}$ 出现的不确定性的大小定义为 $\large x_{i}$ 所携带的信息量，用 $I(x_{i})$ 表示。 $I(x_{i})$ 与信息 $\large x_{i}$ 出现的概率 $P(x_{i})$ 之间的关系为

$\begin{aligned} I(x_i) = & log\frac{1}{P(x_i)} = -logP(x_i) \tag{1} \\ \end{aligned}$

例：掷两枚骰子，求点数和为7的信息量点数和为7的情况为：(1,6) ; (6,1) ; (2,5) ; (5,2) ; (3,4) ; (4,3) 这6种。总的情况为 6*6 = 36 种。
那么该信息出现的概率为 $P_{x=7}=\frac{6}{36}=\frac{1}{6}$
包含的信息量为 $I(7)=-\log P(7)=-\log\frac{1}{6}=\log 6$

以上是求单一信息的信息量。但实际情况中，会要求我们求多个信息的信息量，也就是平均信息量。

假设一共有 n 种信息，每种信息出现的概率情况由以下列出：

$X_1$	$X_2$	$X_3$	$X_4$	$.....$	$X_n$
$P(x_1)$	$P(x_2)$	$P(x_3)$	$P(x_4)$	…	$P(x_n)$

同时满足：
$\begin{aligned} \sum^n_{i=1} P(x_i) = 1 \tag{2} \\ \end{aligned}$

则 $x_1,x_2,.....,x_n$ 所包含的信息量分别是 $KaTeX parse error: Undefined control sequence: \logP at position 2: -\̲l̲o̲g̲P̲(x_1),-\logP(x_…$ 平均信息量为
$KaTeX parse error: Undefined control sequence: \logP at position 49: …^n_{i=1} P(x_i)\̲l̲o̲g̲P̲(x_i) \tag{3} \…$

H 与热力学中的熵的定义类似，故这又被称为信息熵。

与热力学中的熵的定义类似，故这又被称为信息熵。
$\begin{aligned}H(x) = -(\frac{1}{8}\log(\frac{1}{8}) + \frac{1}{8}\log(\frac{1}{8}) + \frac{1}{4}\log(\frac{1}{4}) + \frac{1}{2}\log(\frac{1}{2}) ) = 1.75 \end{aligned}$

连续信息的平均信息量可定义为

$\begin{aligned} H(x) = -\int f(x)\log f(x)dx \tag{3} \end{aligned}$

这里的 $f (x)$ 是信息的概率密度。

上述我们提到了信息论中的信息熵
$\begin{aligned} H(x) = -\sum^n_{i=1}P(x_i) \log P(x_i) = \sum^n_{i=1} P(x_i) \log \frac{1}{P(x_i)} = H(P) \tag{4} \end{aligned}$

这是一个平均信息量，又可以解释为：用基于P的编码去编码来自P的样本，其最优编码平均所需要的比特个数

接下来我们再提一个概念：交叉熵

$\begin{aligned} H(P,Q) = -\sum^n_{i=1}P(x_i) \log Q(x_i) = \sum^n_{i=1} P(x_i) \log \frac{1}{Q(x_i)} \tag{6} \end{aligned}$

这就解释为：用基于P的编码去编码来自Q的样本，所需要的比特个数

【注】 $P (x)$ 为各字符出现的频率， $\log \frac{1}{P(x)}$ 为该字符相应的编码长度， $\log \frac{1}{Q(x)}$ 为对应于Q 的分布各字符编码长度。

KL 散度

让我们从一个问题开始我们的探索。假设我们是太空科学家，正在访问一个遥远的新行星，我们发现了一种咬人的蠕虫，我们想研究它。我们发现这些蠕虫有10颗牙齿，但由于它们不停地咀嚼，很多最后都掉了牙。在收集了许多样本后，我们得出了每条蠕虫牙齿数量的经验概率分布:
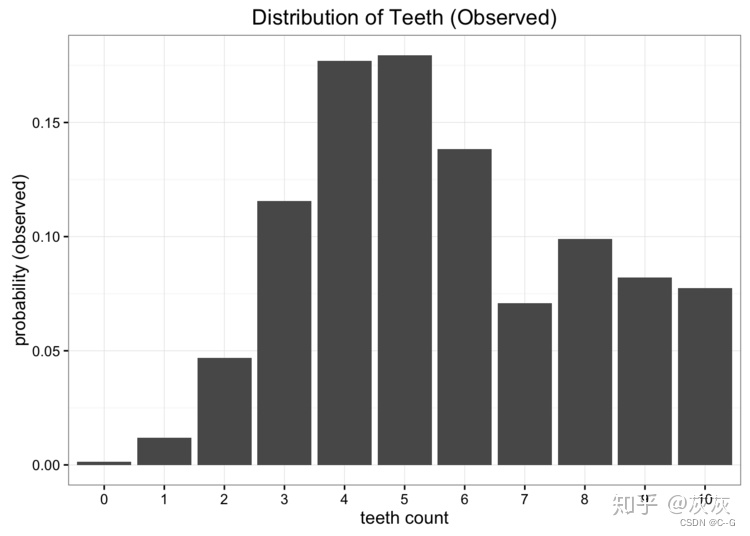
在这里插入图片描述
虽然这些数据很好，但我们有一个小问题。我们离地球很远，把数据寄回家很贵。我们要做的是将这些数据简化为一个只有一两个参数的简单模型。一种选择是将蠕虫牙齿的分布表示为均匀分布。我们知道有11个可能的值，我们可以指定1/11的均匀概率
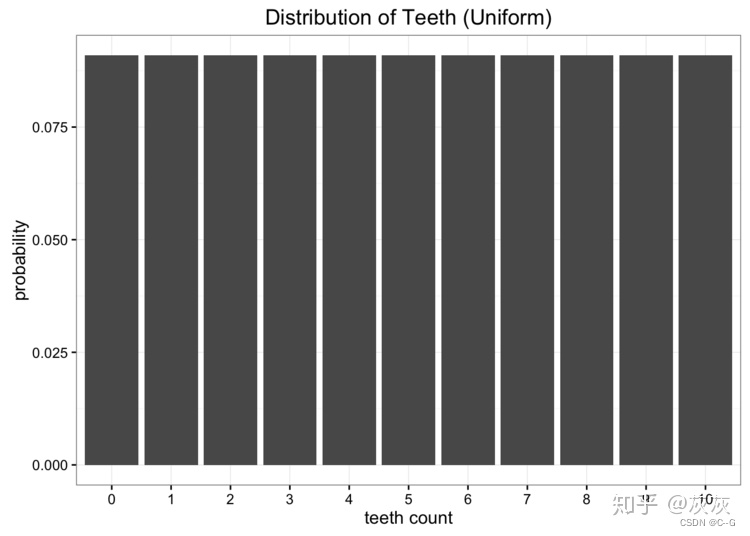
在这里插入图片描述
显然，我们的数据不是均匀分布的，但是看起来也不像我们所知道的任何常见分布。我们可以尝试的另一种选择是使用二项分布对数据进行建模。在这种情况下，我们要做的就是估计二项分布的概率参数。我们知道如果我们有n次试验，概率是p，那么期望就是E[x]= np。在本例中n = 10，期望值是我们数据的平均值，计算得到5.7，因此我们对p的最佳估计为0.57。这将使我们得到一个二项分布，如下所示：

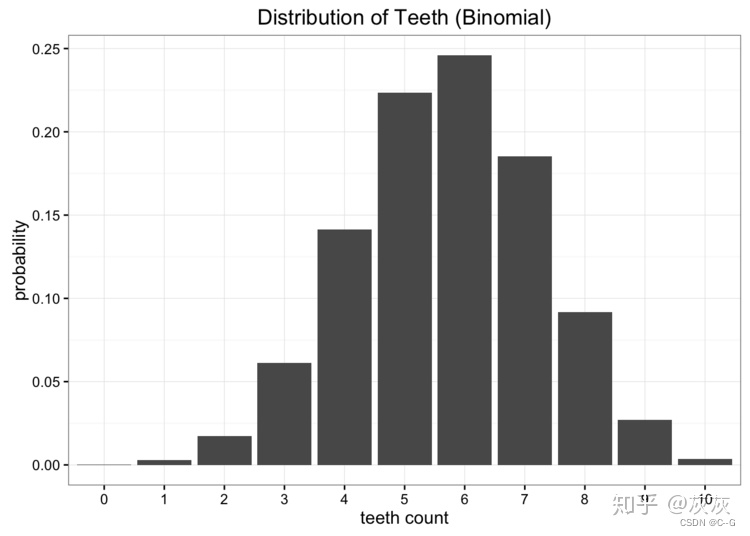
在这里插入图片描述
将我们的两个模型与原始数据进行比较，我们可以看出，两个都没有完美匹配原始分布，但是哪个更好？

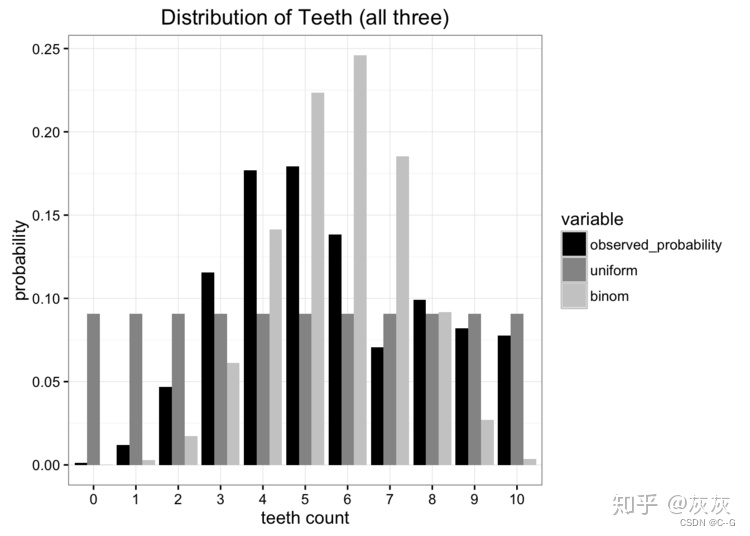
现如今有许多错误度量标准，但是我们主要关注的是必须使发送的信息量最少。这两个模型都将我们的问题所需的参数量减少。最好的方法是计算分布哪个保留了我们原始数据源中最多的信息。这就是Kullback-Leibler散度的作用。

KL散度又可称为相对熵，描述两个概率分布 P 和 Q 的差异或相似性，用 $D_{KL}(P\left | \right |Q)$ 表示

$\begin{aligned} D_{KL}(P || Q) & = H(P,Q) - H(P) \\ & = \sum_i P(x_i) \log \frac{1}{Q(x_i)} - \sum_i P(x_i) \log \frac{1}{P(x_i)} \\ & = \sum_i P(x_i) \log \frac{P(x_i)}{Q(x_i)} \tag{7} \\ \end{aligned}$