一、本周周赛总结

• 可能上周太难了，这周题目简单一些。
• T1 前/后缀和+遍历。
• T2 利用同余模拟，这题粗心忘记取模wa一次。
• T3 排序+双指针，想错了wa一次。
• T4 带限制条件的最短路，堆+bfs，脑子抽了一开始写了个队列bfs ， TLE。

二、 [Easy] 6369. 左右元素和的差值

链接: 6369. 左右元素和的差值

1. 题目描述

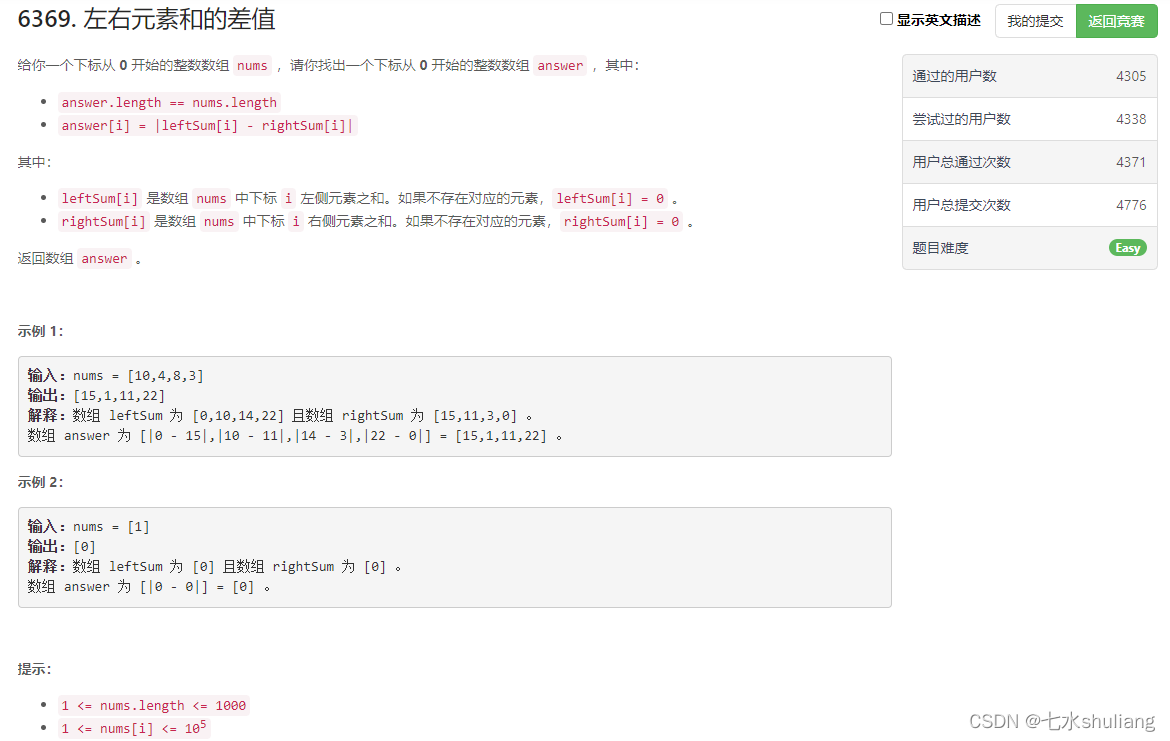
2. 思路分析

计算出左右部分模拟即可。

3. 代码实现

class Solution:
    def leftRigthDifference(self, nums: List[int]) -> List[int]:
        s = sum(nums)
        n = len(nums)
        ans = [0] *n 
        p  = 0
        for i in range(n):
            s -= nums[i]
            ans[i] =  abs(p - s)
            p += nums[i]
        return ans

三、[Medium] 6368. 找出字符串的可整除数组

链接: 6368. 找出字符串的可整除数组

1. 题目描述

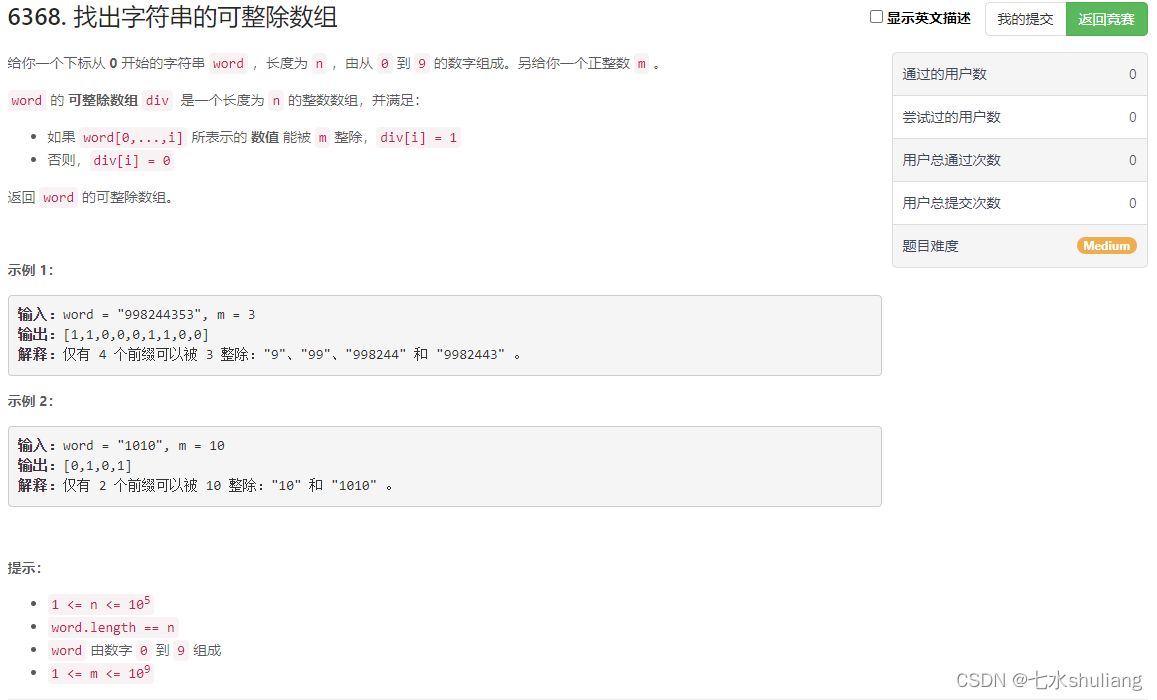
2. 思路分析

• 利用同余的性质，可以每次都把结果取模，留下的数对m取模结果是一样的。

3. 代码实现

class Solution:
    def divisibilityArray(self, word: str, m: int) -> List[int]:
        n = len(word)
        ans = [0]*n
        p = 0
        for i,v in enumerate(word):
            p = (p*10 + int(v))%m
            if p % m == 0:
                ans[i] = 1
        return ans

四、[Medium] 6367. 求出最多标记下标

链接: 6367. 求出最多标记下标

1. 题目描述

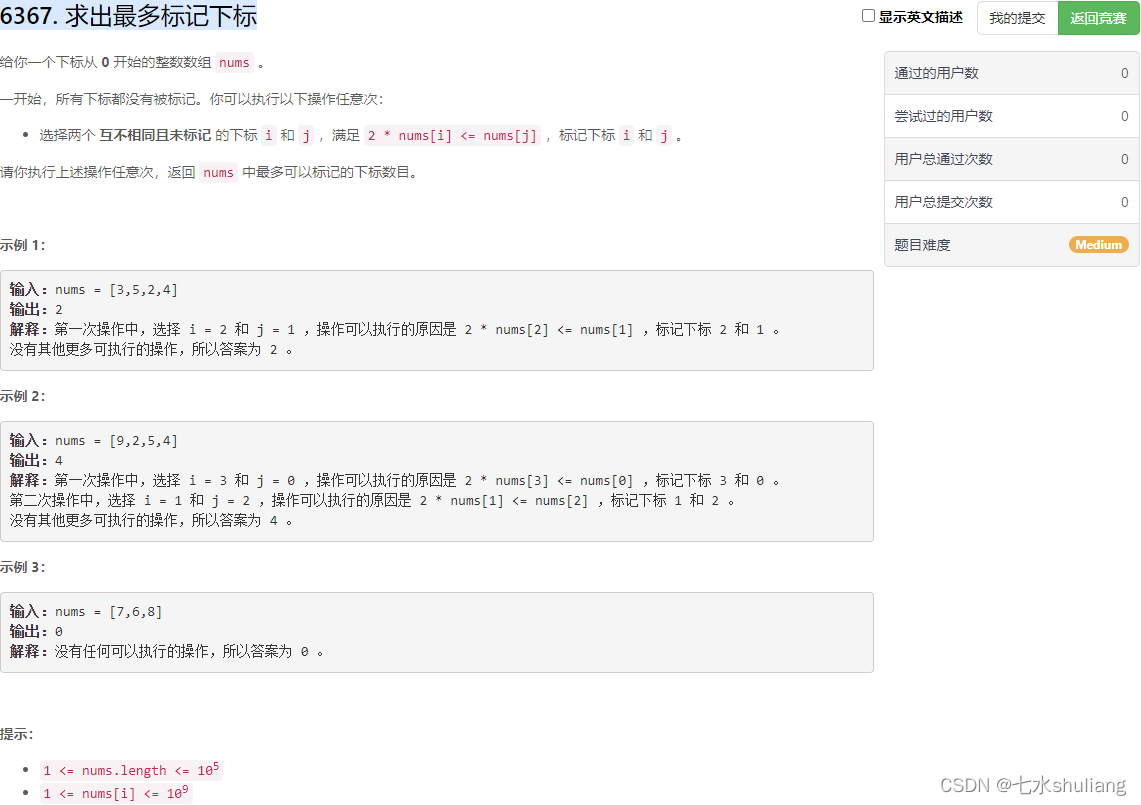
2. 思路分析

• 显然最多可以组成n/2对，即长度n。
• 那么贪心的想，最大的数应该和谁匹配呢，从所有可以匹配的数种找最大值匹配，剩下的数更有可能匹配。
• 那么排序后，前后两半双指针从后边贪心即可。

3. 代码实现

class Solution:
    def maxNumOfMarkedIndices(self, nums: List[int]) -> int:
        n = len(nums)
        nums.sort()
        if n == 1:
            return 0
        r = n-1
        l = (n-1) // 2
        ans = 0
        for r in range(n-1,l,-1):
            while l>=0 and nums[l]*2 >nums[r]:
                l -= 1
            if l < 0:
                break
            ans += 2
            l -= 1
        return ans        

五、[Hard] 6366. 在网格图中访问一个格子的最少时间

链接: 6366. 在网格图中访问一个格子的最少时间

1. 题目描述

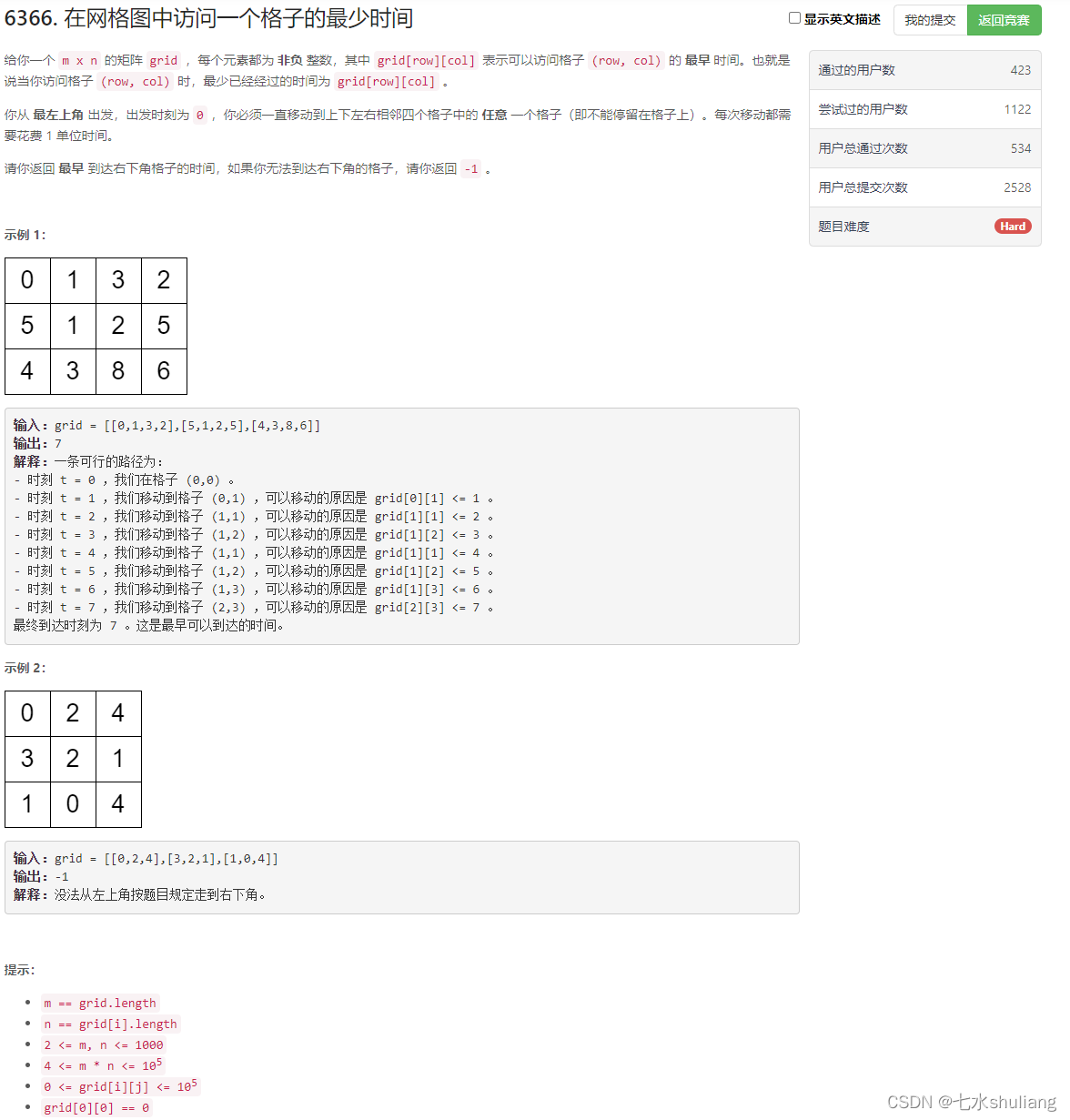
2. 思路分析

• 先讨论无法到达的情况：题目限制0,0位置是0一定可以出发，相邻的格子(0,1),(1,0)只能第一步到达，如果他们同时>1，则将被困在起点无法出发，返回-1。（注意数据限制2<=m,n）
• 若这两个位置能走出去，那么其他位置一定可以通过在相邻附近某两个格子反复横跳的方式等到时间够用(即>grid[i][j])，一定有解。
• 那么用小顶堆写个bfs即可。
• 注意，(x,y)和起点差奇数步的话，到达(x,y)的时间也只能是奇数步，因为反复横跳步数是+2的。
  • 因此当遇到奇数步w = grid[x][y]时，到达(x,y)的时间一定是超过当前步数+1，且奇数，即>=w的第一个奇数。
• 偶数同理。

3. 代码实现

DIRS = [(0,1),(1,0),(0,-1),(-1,0)]
class Solution:
    def minimumTime(self, grid: List[List[int]]) -> int:
        m,n = len(grid),len(grid[0])
        ans = -1
        if grid[0][1] > 1 and grid[1][0] > 1:
            return -1
        vis = [[10**6]*n for _ in range(m)]
        vis[0][0] = 0
        def inside(x,y):
            return 0<=x<m and 0<=y<n
        q = [(0,0,0)]
        while q:
            d,x,y = heappop(q)
            
            for dx,dy in DIRS:
                a,b = x+dx,y+dy
                if inside(a,b) and vis[a][b] >  vis[x][y] + 1:                   
                    w = grid[a][b]
                    if w <= vis[x][y] + 1:
                        vis[a][b] = vis[x][y] + 1
                        # q.append((a,b))
                        heappush(q,(vis[a][b],a,b))
                        
                    elif (a+b)%2 == 0:
                        vis[a][b] = w if w%2==0 else w + 1
                        heappush(q,(vis[a][b],a,b))
                    else:
                        vis[a][b] = w if w%2==1 else w + 1
                        heappush(q,(vis[a][b],a,b))
                    if a == m-1 and b == n-1:
                        return vis[a][b]
                        
        return vis[m-1][n-1]
                        
                

六、参考链接