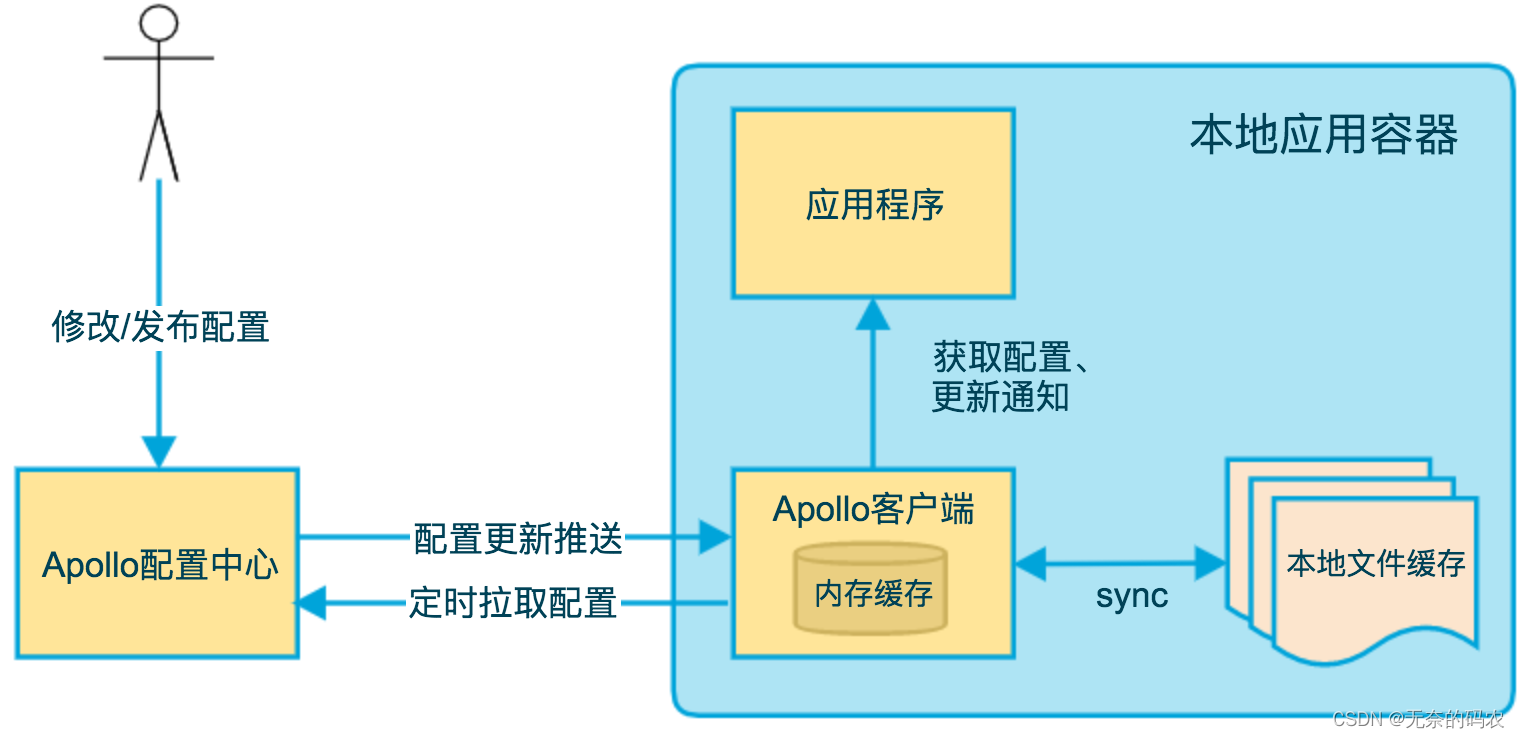
记录研究生课程模拟集成电路设计所学到的一些知识，这门课是由刘老师和周老师一起上的，刘老师讲模拟集成部分这个模集跟模电还是有很大的区别的，模拟集成主要是针对MOS器件的集成，学得更专业也更深；而周老师讲的是信号检测部分，就是模拟集成电路的应用。纯粹个人笔记，学到了就更。。。

🚀模拟集成电路篇

1、MOS管的模型

(1)最简模型
MOS的最简模型就是一个开关，栅极电压V_G控制漏极和源极的通断。

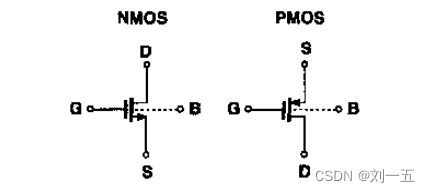
（2）如何识别NMOS和PMOS
首先，箭头所在的一极为源极；
箭头表示电流的方向，往外流的是NMOS，往里面流的是PMOS。
NMOS管漏极电压V_D>源极电压V_S；而PMOS则刚好相反，漏极电压V_D<源极电压V_S.

（3）对控制过程的理解

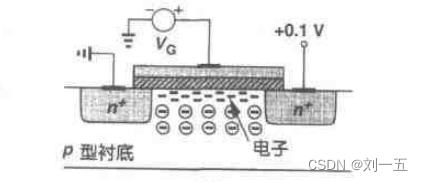
首先，V_G将电子吸到漏极D和源极S之间；接着，加V_DS使这个电子块有了电压而运动起来。

2、二级效应

MOS管要考虑的二级效应主要有：体效应、沟道调制效应、亚阈值导电效应。
(1) 体效应
MOS管的阈值电压如下：
$$V_{TH}=V_{TH0}+\gamma (\sqrt{|2{\varphi }_F+V_{SB}|}-\sqrt[]{|2{\varphi }_F|})$$
其中，VTH0是由工艺决定的，而VSB是栅极—衬底电压。
体效应就是衬底和源极的电压差对阈值电压的影响。

并且漏极电流：
$$I_D=I_1=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L}(V_{in}-V_{out}-V_{TH}{)}^2$$
当输入的Vin保持不变时，VTH的变大会导致Vout的变小，如下图所示。

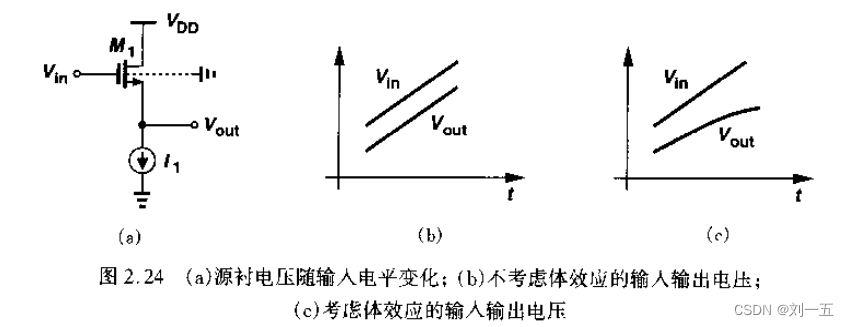
体效应是可以消除的，只要式子中的VSB=0即可，这就需要将衬底和源极短接起来。比如在集成时让PMOS独占一个阱，使得NMOS与PMOS的衬底都能与源极短接起来。

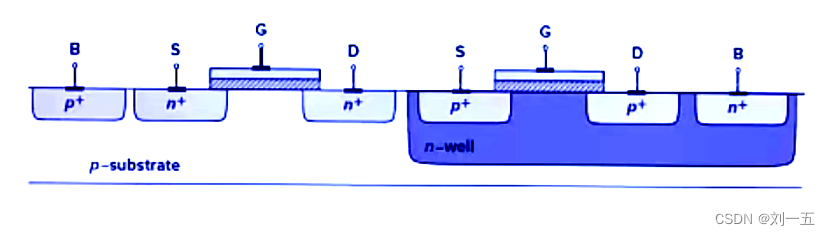
(2) 沟道调制效应
沟道调制效应指的就是沟道长度变化对于漏极电流$I_D$以及跨导$g_m$的调制作用。

在不考虑沟道调制效应的情况下，漏极电流：
$$I_D=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_{TH}{)}^2$$
但由于沟道调制效应，L的大小发生了变化，用L’表示：
$$L^{{}^{\prime }}=L-\Delta L$$
则：
$$\frac{1}{L^{{}^{\prime }}}=\frac{1}{L-\Delta L}=\frac{1}{L}(\frac{1}{1-\frac{\Delta L}{L}})=\frac{1}{L}(\frac{1-\frac{\Delta L}{L}+\frac{\Delta L}{L}}{1-\frac{\Delta L}{L}})=\frac{1}{L}(1+\frac{\Delta L}{L-\Delta L})$$
且当$\Delta L<<L$时
$$\frac{1}{L^{{}^{\prime }}}=\frac{1}{L}(1+\frac{\Delta L}{L})$$
又$$\frac{\Delta L}{L}=\lambda V_{DS}$$
故：$$I_D=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L^{{}^{\prime }}}(V_{GS}-V_{TH}{)}^2=\frac{1}{2}{\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_{TH}{)}^2(1+\lambda V_{DS})$$

从而引起I-V曲线在饱和区的上翘：

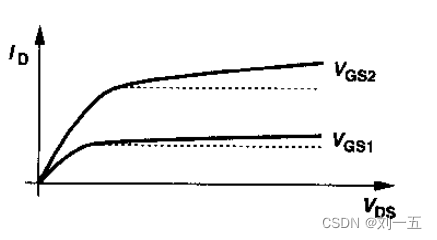
同样的，在不考虑沟道调制效应时：
$$g_m={\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_{TH})$$
考虑沟道调制效应后：
$$g_m={\mu }_n{C}_{ox}\frac{W}{L}(V_{GS}-V_{TH})(1+\lambda V_{DS})$$

沟道调制效应与体效应不同，沟道调制效应无法消除，但是可以减弱。要想减弱沟道调制效应，根据公式，无非就是考虑deltaL减小或者是L的变大。delta的减小也就是让MOS器件工作在预夹断点附近，但我们需要一定的摆幅来使得信号不失真，所以这个方法不太可行。而L的变大也就是使用长沟道器件，相比于上一个方法，更为可行。

(3) 亚阈值导电效应

在理想情况下，当栅源电压VGS<阈值电压VTH时，MOS管截止，而实际上，在小于阈值的时候，也就是亚于阈值的时候，MOS也是导通并具有一定的漏极电流ID的，这种现象就成为亚阈值导电效应。

3、从各个极看进去的电阻

通常我们会求输入电阻和输出电阻

发现一个规律：
（1）从栅极看进去，电阻无穷大
比如，共漏极，信号从栅极输入，故，输入电阻无穷大

（2）从源极看进去，电阻为$\frac{1}{g_m+g_{mb}}$
比如，共漏极，信号从源极输出，故，输出电阻为$\frac{1}{g_m+g_{mb}}$
再比如，共栅极，信号从源极输入，故，输入电阻为$\frac{1}{g_m+g_{mb}}$

🚀微弱信号检测篇

1、线性度、弛豫、响应时间

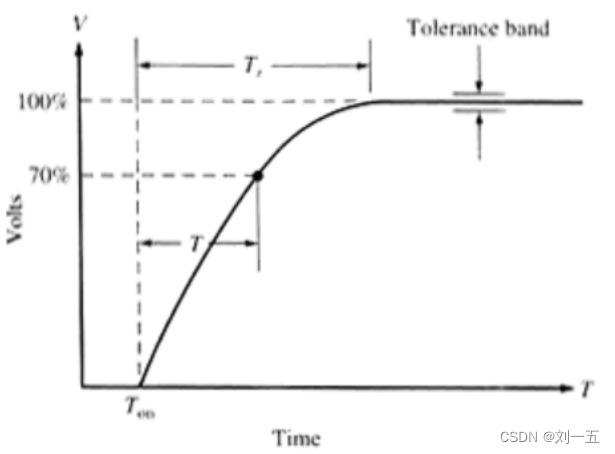
线性度：动态范围内与理想线性传递函数的最大偏差。

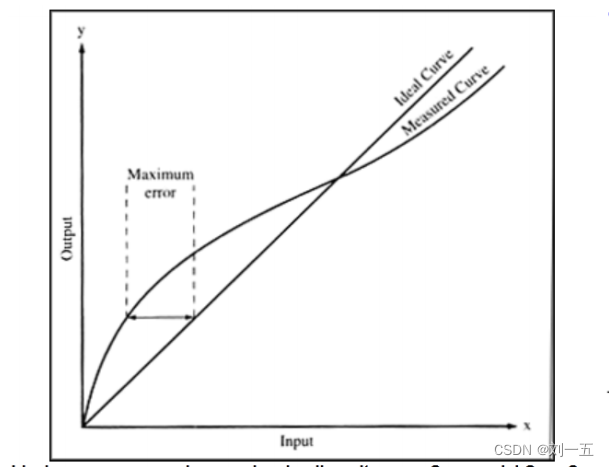
弛豫：物理激发的滞后效应。

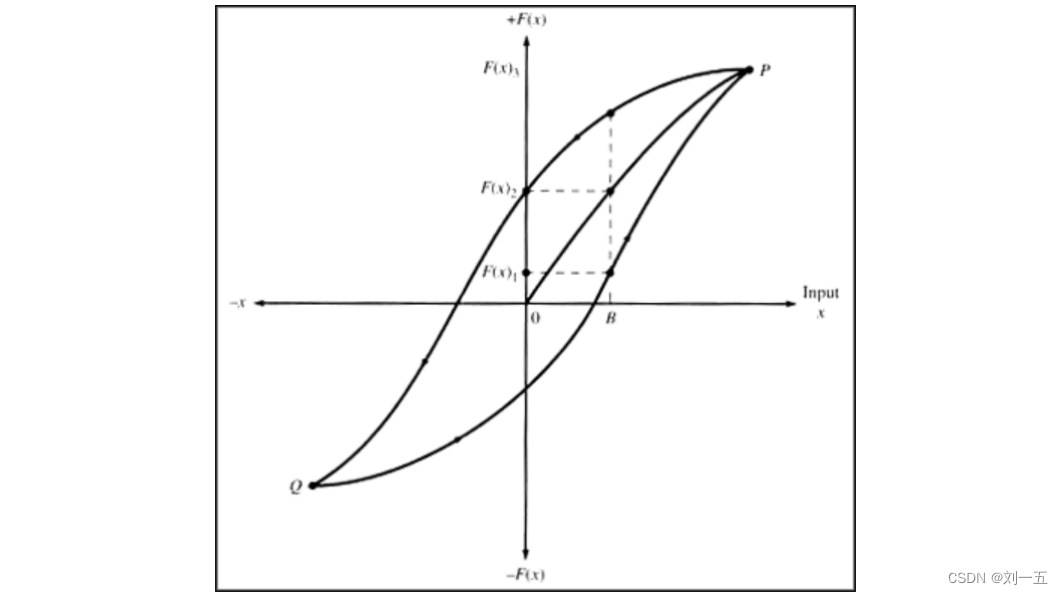
响应时间：从先前状态到最终确定值所需要的时间。

2、准确度、精度、分辨率、灵敏度的区别

准确度：测量值与真实值的接近程度。准确度越高，测量值与真实值就越接近。

精度：重复实验测量得到同一数值的可重复性。精度越高，意味着对同一条件下的测量对象进行重复测量得到同一数值的可重复性更强。

分辨率：可检测的增量大小。分辨率更高，增量越小。

灵敏度：能够响应的最小信号变化程度。灵敏度越高，能测量到的信号变化更微小。

3、奈奎斯特定律

当采样频率大于信号中最高频率的2倍时(fs>2f)，采样之后的数字信号完整地保留了原始信号中的信息。工程上一般采用fs>2.5f。

所以如果用250MHz的采样率采样200MHz的正弦信号，则采样得到的信号会失真。

4、根号m定理

信号平均技术的基本原理— $\sqrt{m}$法则:经过 m 次采样后，信噪比的改善度与$\sqrt{m}$成正比。

5、通过带宽来改善信噪比

随机噪声的有效值与带宽存在以下关系：
$$\frac{V_{rms1}}{V_{rms2}}=\frac{\sqrt{B_1}}{\sqrt{B_1}}$$
所以当通过带通滤波将带宽减小到原来的$\frac{1}{N}$时，噪声将减小为原来的$\frac{1}{\sqrt{N}}$，信噪比提高为原来的$\sqrt{N}$。

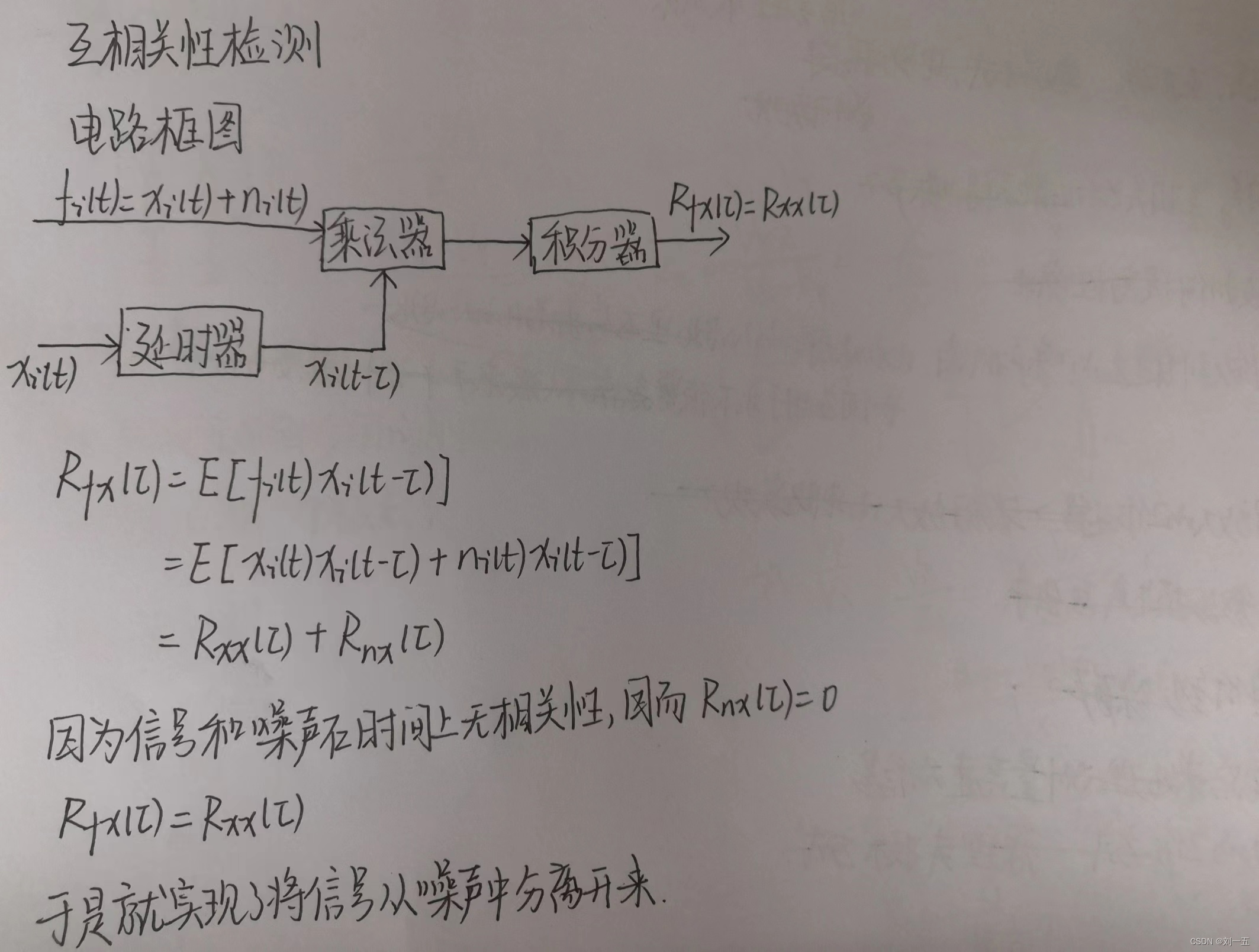
6、自相关检测与互相关检测

相关检测的原理就是：噪声在时间上不相关，而信号在时间上相关。

（1）自相关检测

自相关就是同一信号在不同时间点的相关性。

（2）互相关检测

互相关就是不同信号之间的相关性。

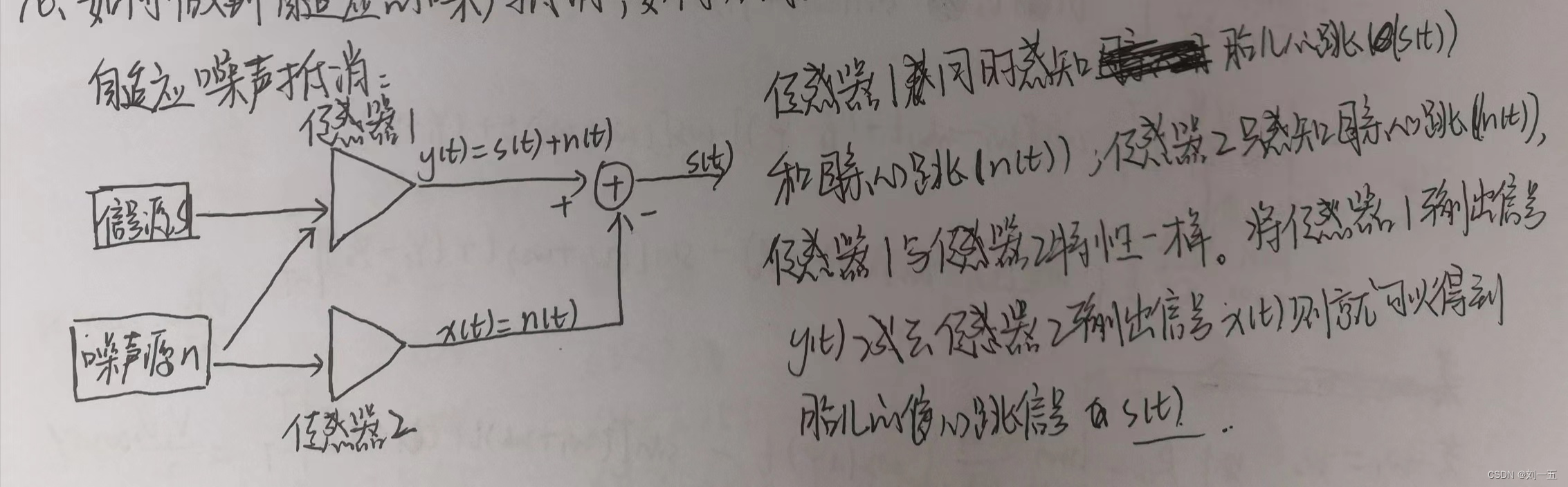
7、自适应噪声抵消

补偿法噪声抵消使得能够在大的噪声环境中检测微弱的信号。比如说如何从母亲的心跳里区分出胎儿的信号？

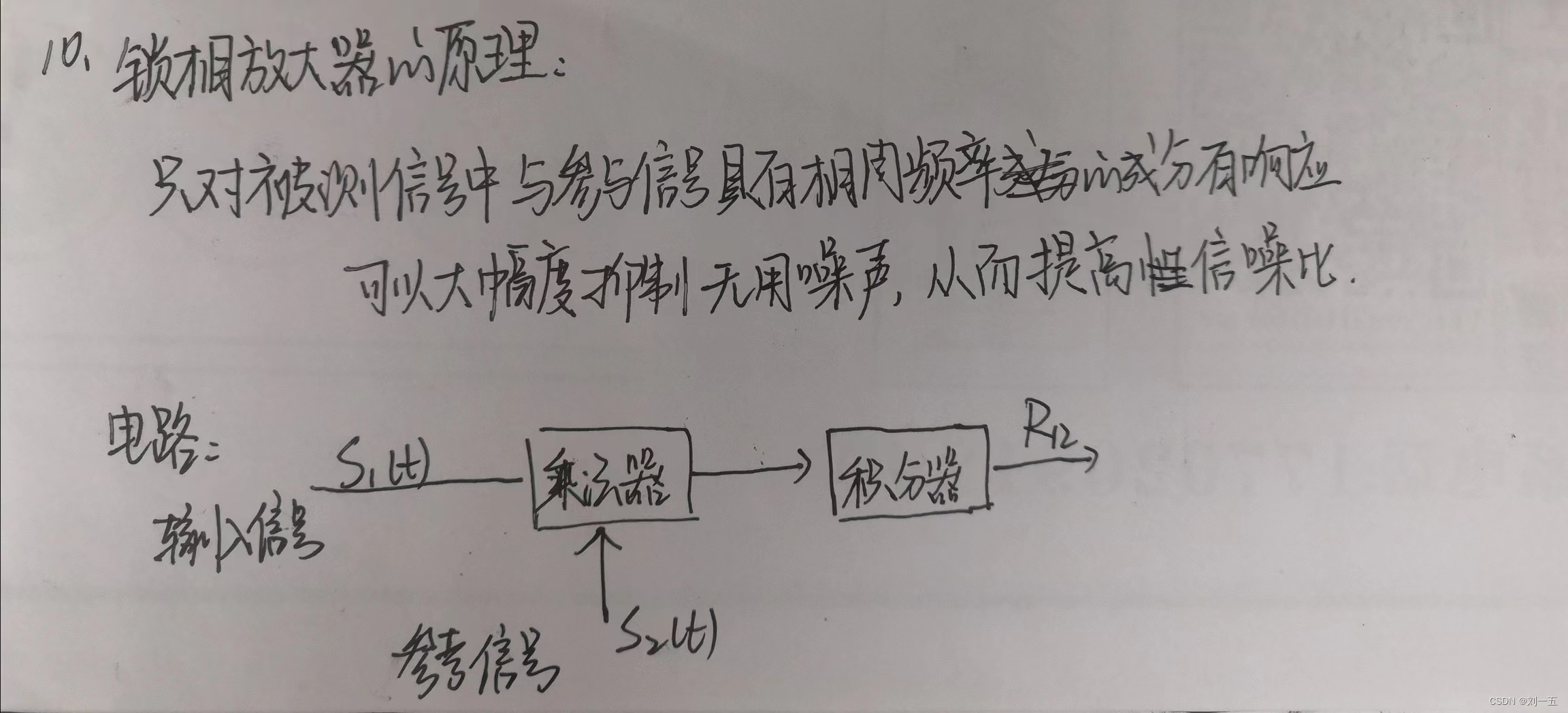
8、锁相放大

9、传感器+菲涅尔透镜

可以用红外传感器来对人体的存在进行检测从而实现灯的开关控制，但是如果当环境的温度高于人体温度的时候，如何实现人体的识别？

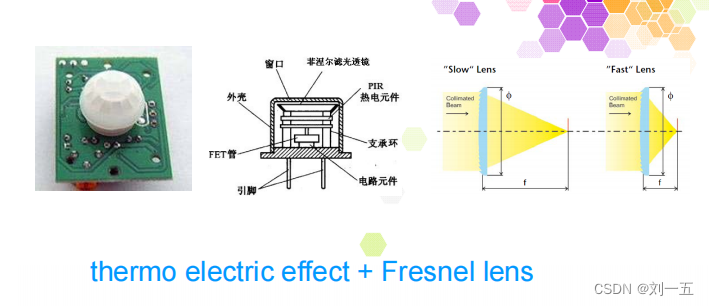
只需要再加一个菲涅尔透镜即可，就是图中的那个白色的盖子。菲涅尔透镜有两个作用，一个是将人红外信息聚焦在探测器上；另一个是将探测器前方的区域分成“盲区”和“高灵敏区”，当人走到探测区域内时，人体发出的红外信号会在“盲区”和“高灵敏区”上交替变换，形成忽强忽弱的脉冲信号，从而将运动的人的信号从静态的环境中区分开来。