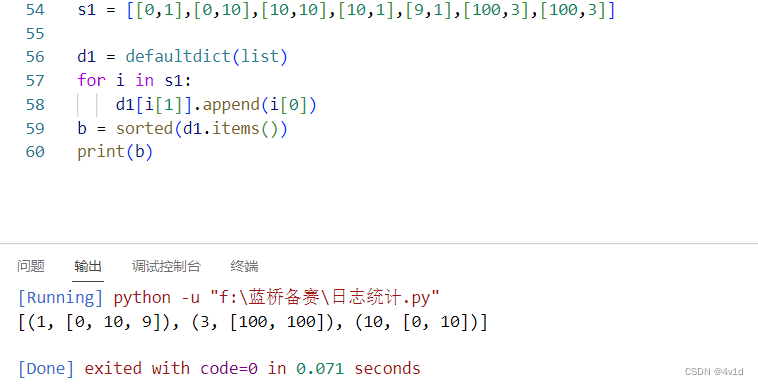
其中Cyrus-Beck算法呢，是计算一根直线一个多边形的交线段；

liang算法是Cyrus的一个特例，即多边形刚好是矩形；

先看看Cyrus算法的思路【从别的博客找的图片】：

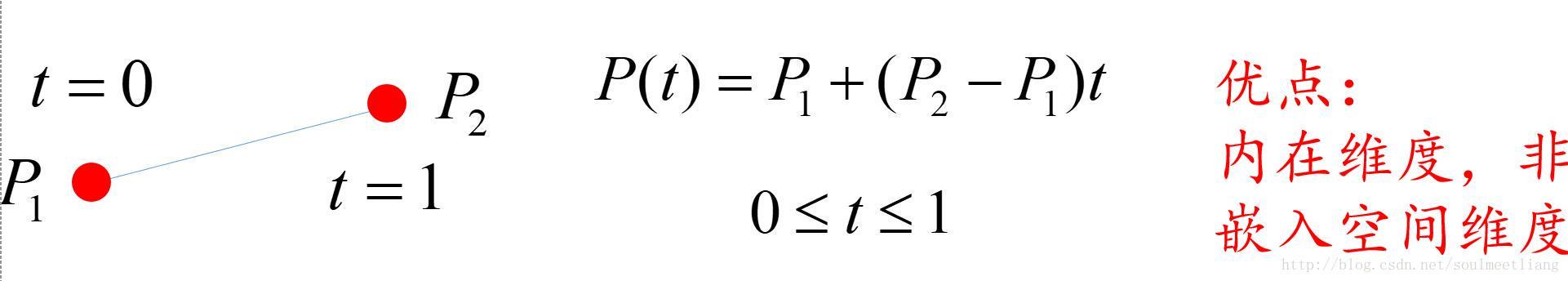
这很容易理解，点积>0时就可能中内部嘛，这就限定了t[直线参数]的一个范围，每个这样的边限定的范围的交集就是t的范围；

这种范围又分为很多种不同的范围，一种是左限制[-nan,i]，一种是右限制[i,+nan]；

这种限制在代数上的意义，是这样推断的，我会给出更形象的个人理解；

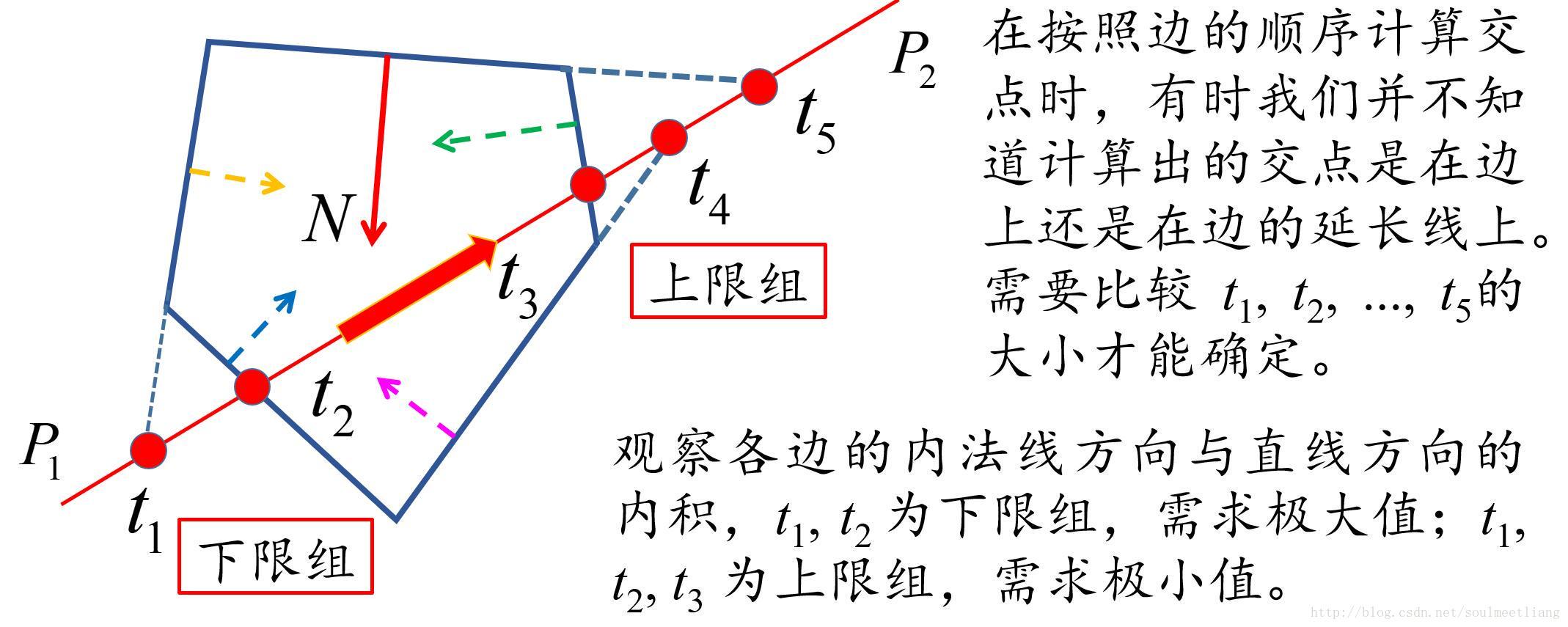
好，我们分成了上限组和下限组，其实这样的几何意义就已经很好理解了；

我个人弄了个更好理解的版本，看啊；

其实上限组顾名思义，其中的线段给出的限定，可以确定t的一个上限，下限组也顾名思义；

那么有了上限和下限，那么确定的t的范围；

拿上面那张图中的N想来和P1P2向量举例子，N向量在P1P2向量的分量是不是向左的？那么N就是属于上限组，分量在P1P2上向右的向量就是下限组；

然后来看看liang算法；

我很好奇，为什么要把这两个算法分开？这是一模一样的的算法；

我刚刚在书上看liang算法的时候一头雾水，变量一代换，中间逻辑直接少了几个环节，看个毛线；

然后去网上查了一下才懂了；

先看看书上的解释：

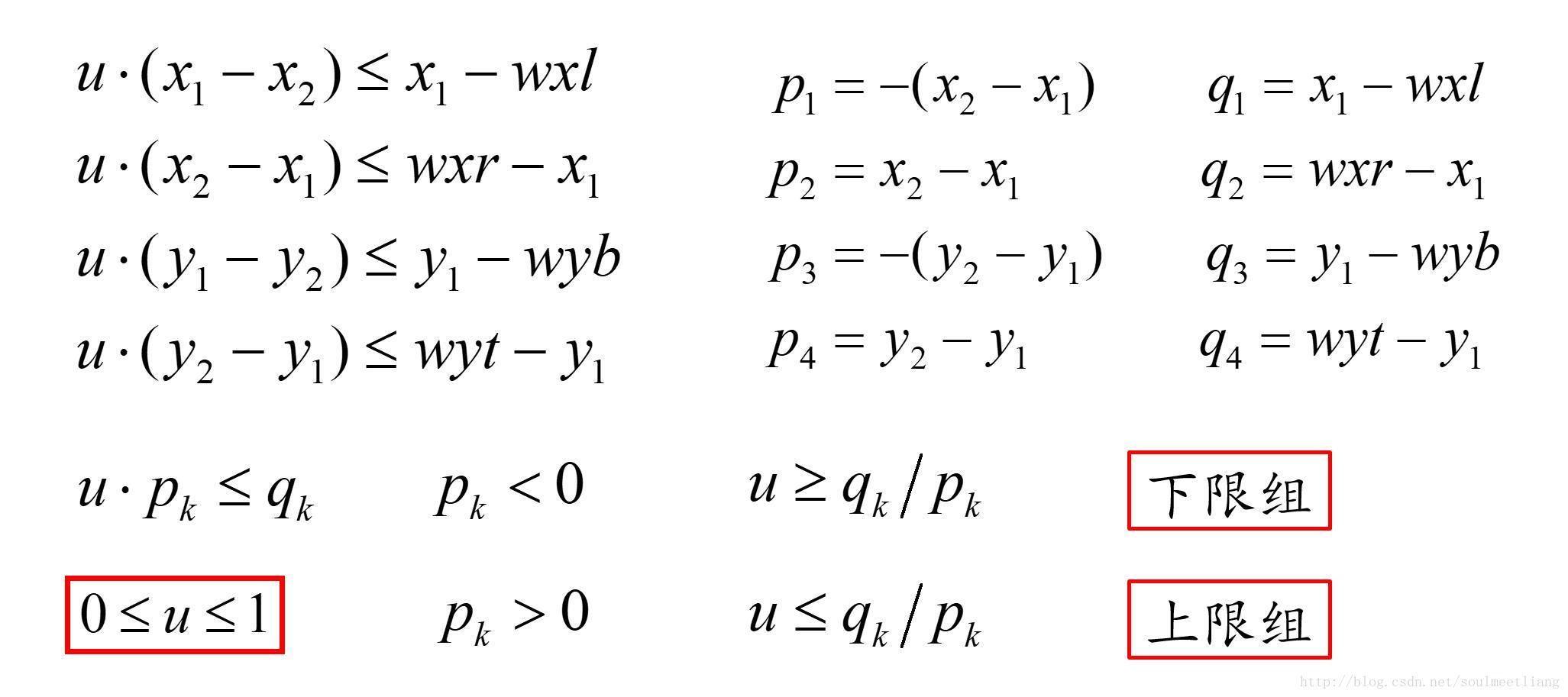
也是确定了上限组和下限组，这张图还好，起码给了上下限组的概念，有的书是完全不给这个概念的；

其实我们可以直接看推：

线段的端点P1(x1,y1),P2(x2,y2)

左边界xl(-lx,0) 右边界xr(lx,0) 下边界yb(0,-lx) 上边界yt(0,lx)；

所以左右边界的内法向量就是[1,0]、[-1,0]

上下边界也一样[0,1]、[0,-1]

那么我们只需要看四个向量在P1P2向量上的分量是向左还是向右就可以知道哪个是上限组哪个是下限组了，当然P1指向P2的方向是向右；

最后的公式也是表示这个意思的；

最后我还有一个发现，但应该也被人发现过，那就是P1P2与四条边界的交点为q1,q2,q3,q4的话，在P1P2与矩形有交集的前提下，对这六个点的x坐标[y坐标也行]进行排序，那么第3、4个点就是需要显示的线段的端点