前言

分页基础概念是操作系统基础知识，网上已经有太多太多了。所以本文记录使用windwow内核调试工具验证理论知识。

具体可以参阅intel volume3的 4.1.1 Four Paging Modes章节。

简而言之：CR0.PG = 0表示不开启分页.并且根据CR4各种标志开启不同类别的分页模式,大致有四种模式。这里贴出原文：

CR4.PAE 开启物理地址扩展简单点理解就是
IA32_EFER.LME 用于启用64位模式（本文讨论范围）
CR4.LA57 CR4.LA57是一个控制寄存器的位，用于启用或禁用所谓的5级分页模式，启用57位线性地址。（本文不讨论，因为现在基本没有使用）
在这里插入图片描述

CR4.LA57 是CR4的第12位，在window10 64位都没有启用(也没有必要启用)

本位讨论的分页机制是原文中的4-level paging分页机制。
这里给出对应原文翻译(仅作参考):

如果 CR4.PAE = 1，IA32_EFER.LME = 1，且 CR4.LA57 = 0，则使用 4 级分页1。4 级分页在第 4.5 节中详细介绍（以及 5 级分页）。
4 级分页使用 CR0.WP、CR4.PGE、CR4.PCIDE、CR4.SMEP、CR4.SMAP、CR4.PKE、CR4.CET、CR4.PKS 和 IA32_EFER.NXE，
如第 4.1.3 节和第 4.6 节所述。

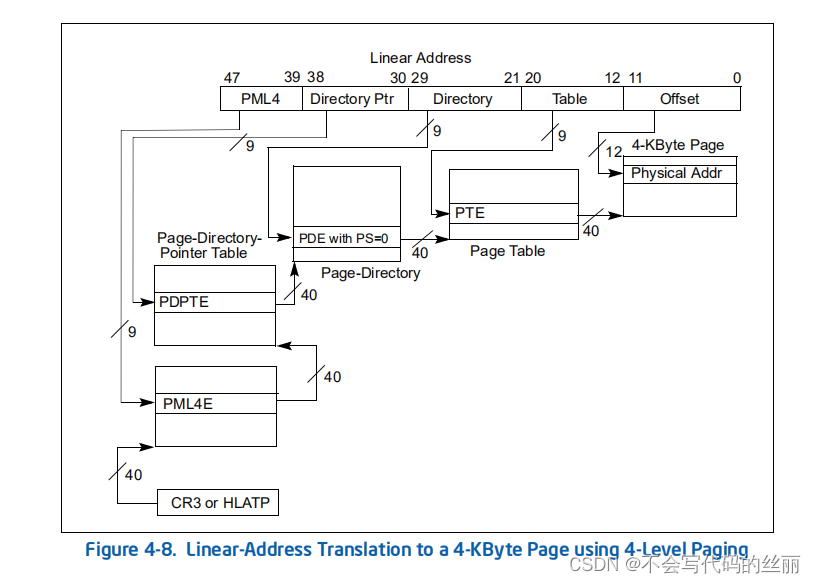
这种分页机制可以存在以下三种分页大小分别为4k ，2M ，1G。具体参阅intel volume3的 4.5.4 Linear-Address Translation with 4-Level Paging and 5-Level Paging章节

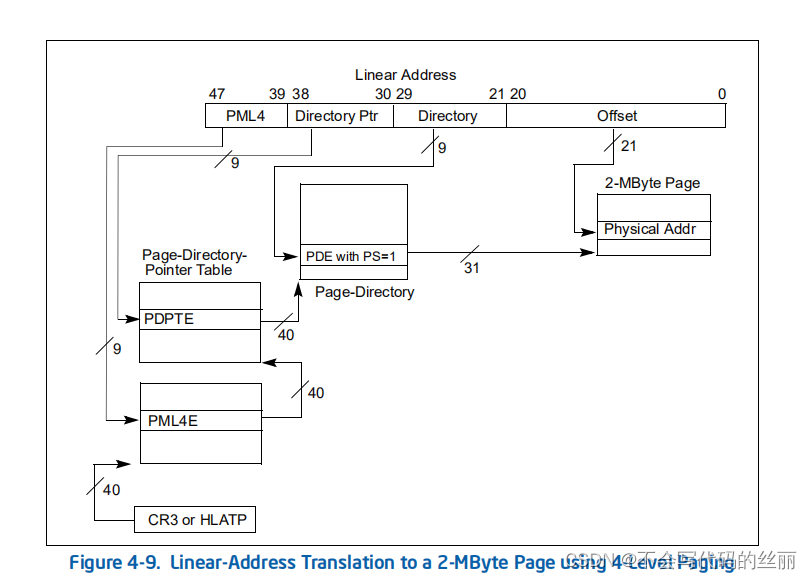
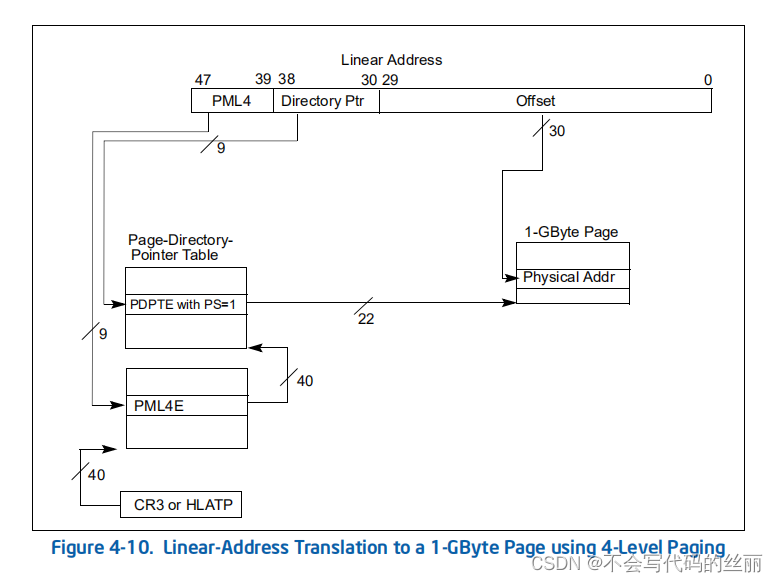
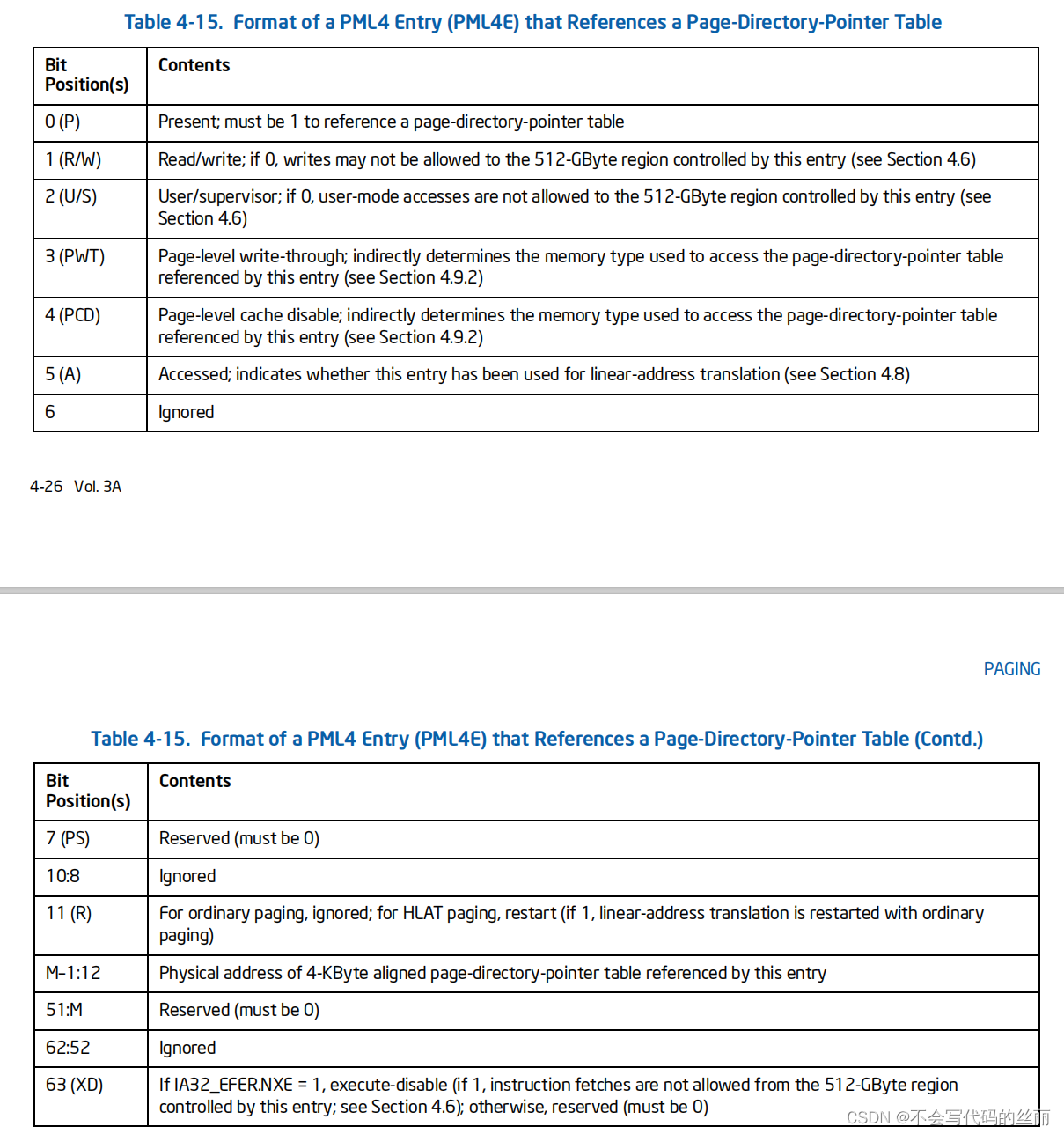
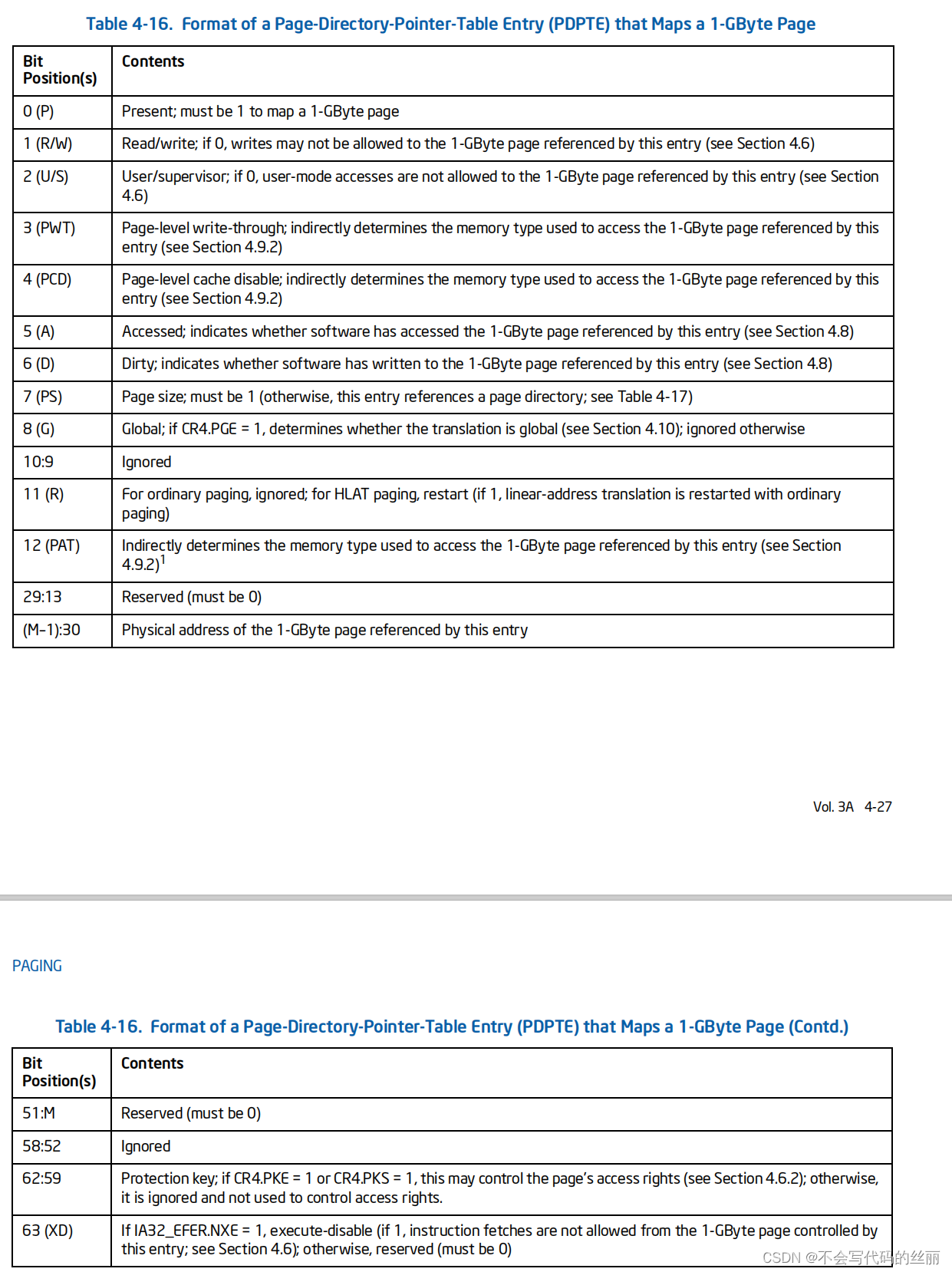
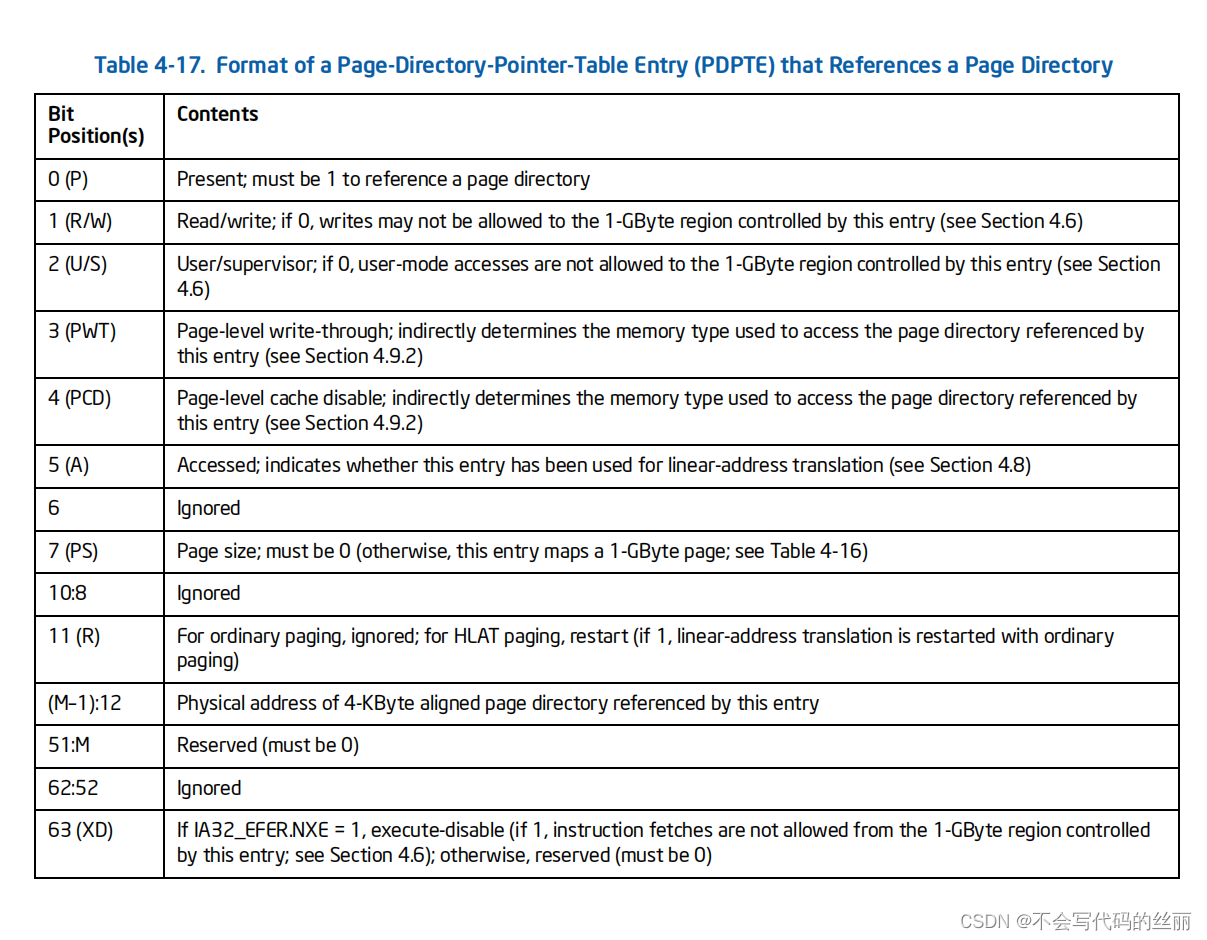
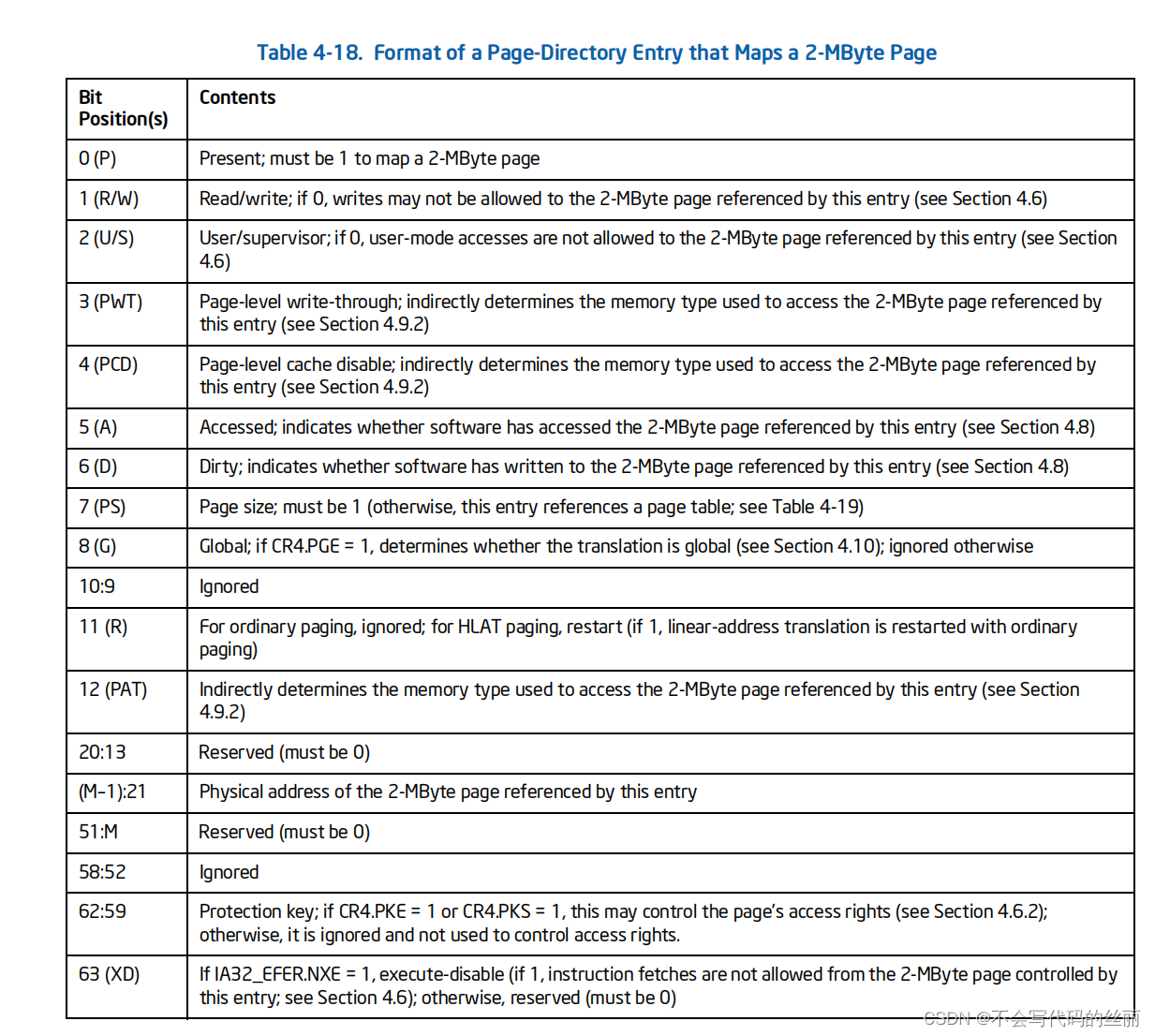
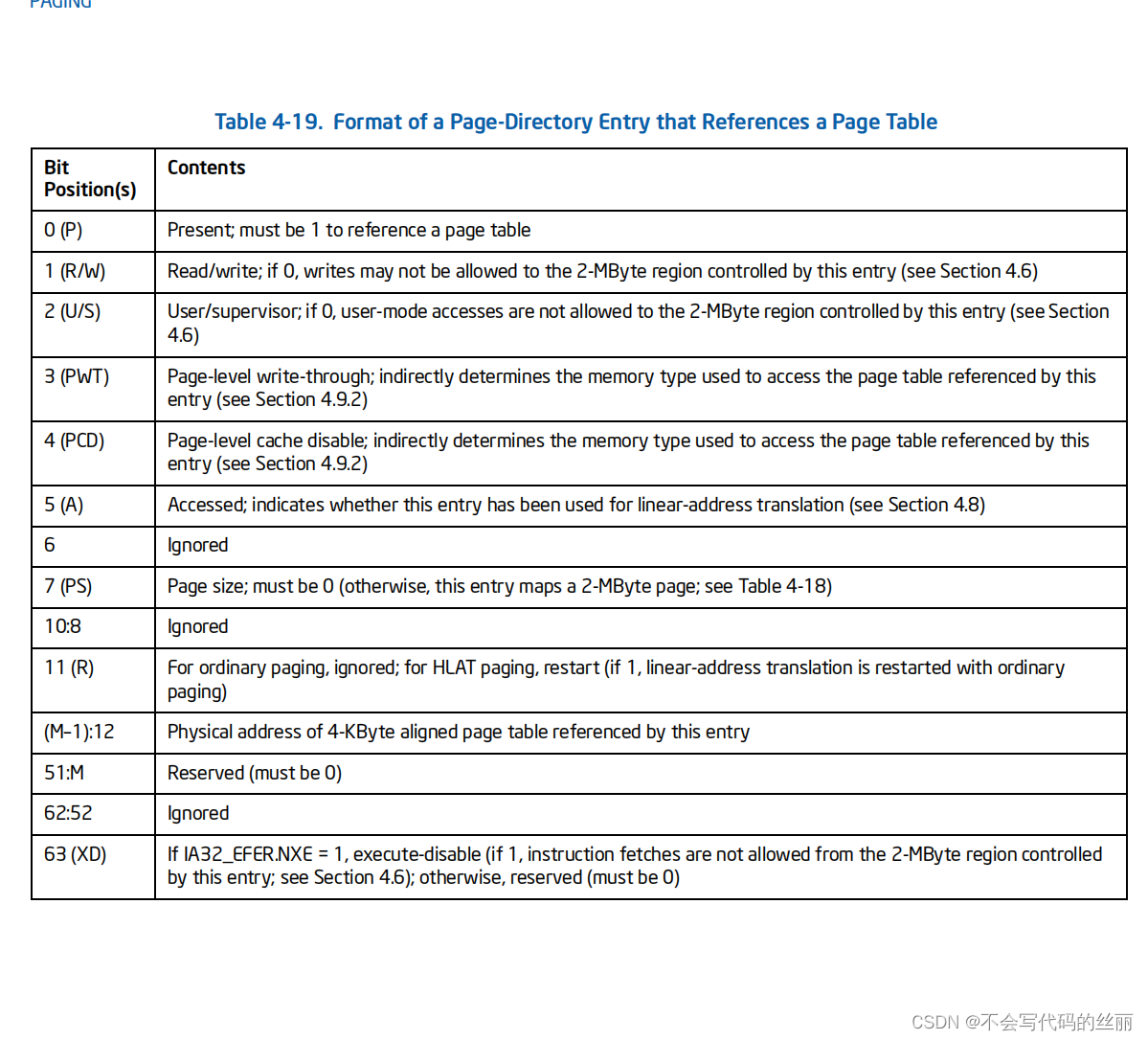
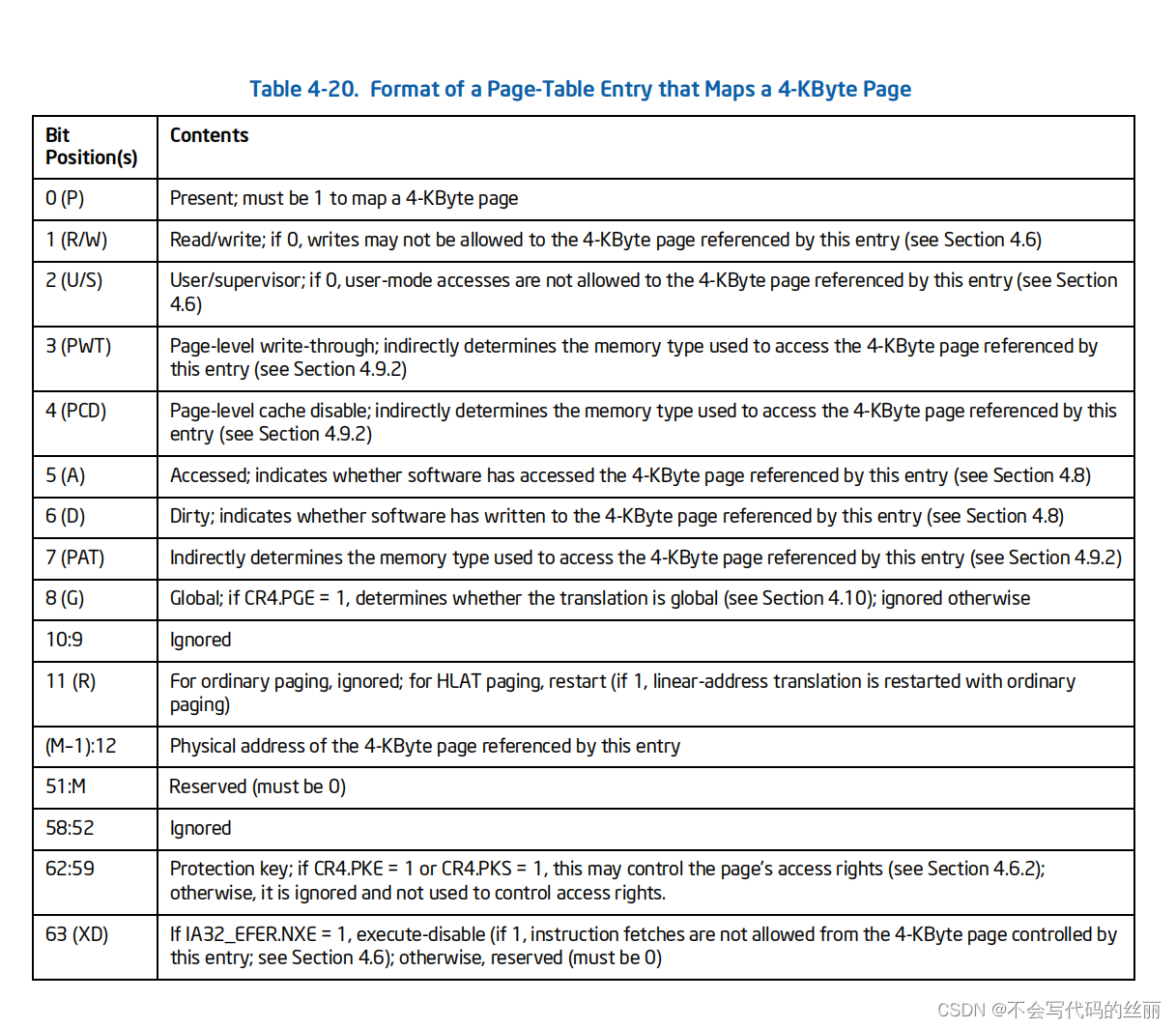
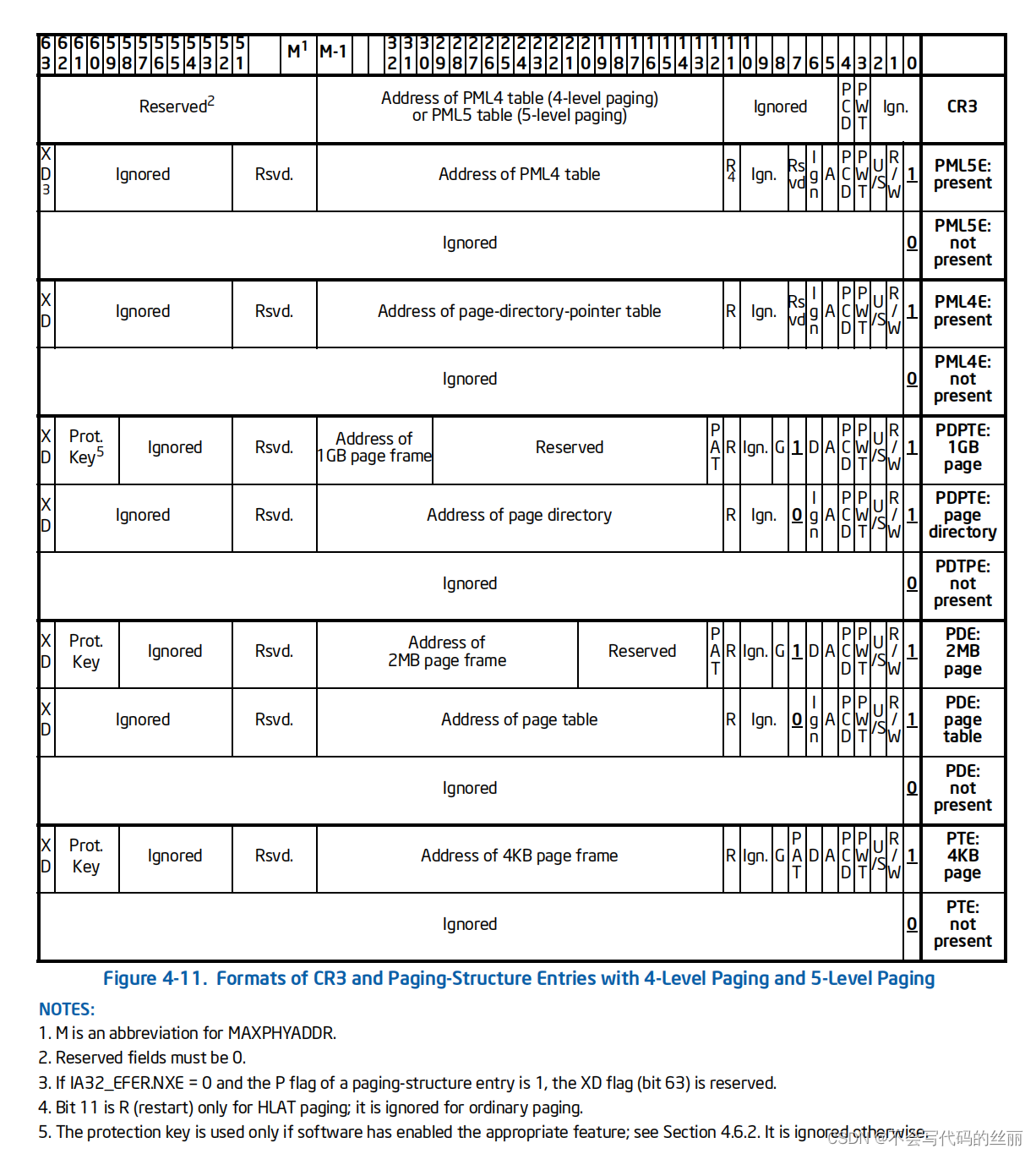
在这里插入图片描述

举例说明

本文以win10 64举例

首先查看cr0.PG用于判断是否开启了分页

1: kd> r cr0
cr0=0000000080050033
1: kd> .formats 0000000080050033
Evaluate expression:
  Hex:     ffffffff`80050033
  Decimal: -2147155917
  Octal:   1777777777760001200063
  Binary:  11111111 11111111 11111111 11111111 10000000 00000101 00000000 00110011
  Chars:   .......3
  Time:    ***** Invalid
  Float:   low -4.59249e-040 high -1.#QNAN
  Double:  -1.#QNAN

我们cr0.PG是第31位，上面可以看到已经设置为1表示已经开启分页。

接着我们查看是否开启了64位

我们首先查看IA32_EFER寄存器。（这是一个MSR，其编号0xC00000801）

//查询寄存器数值
1: kd> rdmsr c0000080
msr[c0000080] = 00000000`00000d01


//打印数值
1: kd> .formats  00000000`00000d01
Evaluate expression:
  Hex:     00000000`00000d01
  Decimal: 3329
  Octal:   0000000000000000006401
  Binary:  00000000 00000000 00000000 00000000 00000000 00000000 00001101 00000001
  Chars:   ........
  Time:    Thu Jan  1 08:55:29 1970
  Float:   low 4.66492e-042 high 0
  Double:  1.64474e-320

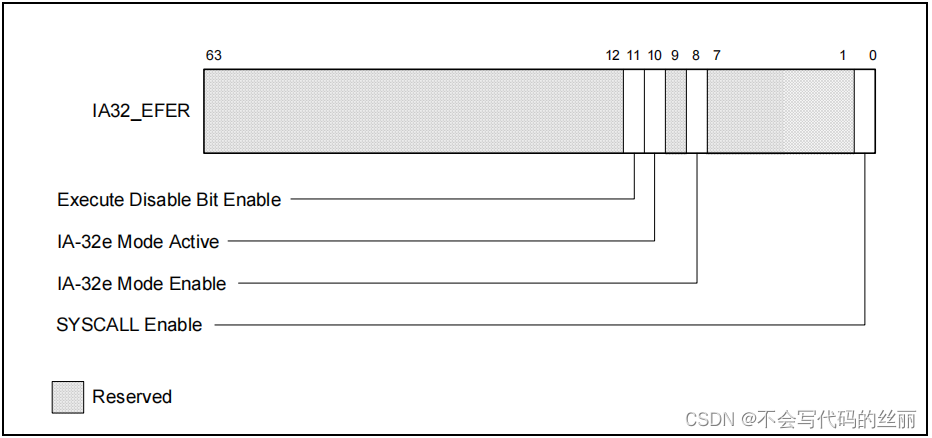
在这里插入图片描述
其中第8和第10位是我们需要关注的，如果是1的话表示开启。（本例已经可以看到已经设置为1），证明已经开启了64位

最后我们分析一下开启哪种分页模式

1: kd> r cr4
cr4=00000000001506f8


1: kd> .formats  00000000001506f8
Evaluate expression:
  Hex:     00000000`001506f8
  Decimal: 1378040
  Octal:   0000000000000005203370
  Binary:  00000000 00000000 00000000 00000000 00000000 00010101 00000110 11111000
  Chars:   ........
  Time:    Sat Jan 17 06:47:20 1970
  Float:   low 1.93105e-039 high 0
  Double:  6.80842e-318

其中PAE是第5位，LA57 是第12位
CR4.PAE = 1， CR4.LA57 = 0 综上本系统开启了level 4的分页模式

我们随便查看一个寄存器的数值：

1: kd> r gdtr
gdtr=ffffd001fee69840
1: kd> dq ffffd001fee69840
ffffd001`fee69840  00000000`00000000 00000000`00000000
ffffd001`fee69850  00209b00`00000000 00409300`00000000
ffffd001`fee69860  00cffb00`0000ffff 00cff300`0000ffff
ffffd001`fee69870  0020fb00`00000000 00000000`00000000
ffffd001`fee69880  fe008be6`2ac00067 00000000`ffffd001
ffffd001`fee69890  7240f36e`90007c00 00000000`00000000
ffffd001`fee698a0  00000000`00000000 00000000`00000000
ffffd001`fee698b0  ecdd8e00`00106100 00000000`fffff800

我们通过计算得到相关偏移：

ffffd001fee69840
对于 4k大小 分页
PML4 =  0x1A0  , Directory ptr = 0x7 , Directory = 0x1F7 , table = 0x69,  offset = 0x840
其他略

//查看页表
1: kd> r cr3
cr3=00000000001ab000

//由于PML4全部8字节的，所以我们计算可以得相关地址位cr3 + 8 *PML4  
最后得到 PML4E=00000000`00125863 

1: kd> !dq  00000000001ab000+8*1A0
#  1abd00 00000000`00125863 00000000`00000000
#  1abd10 00000000`00000000 00000000`00000000
#  1abd20 00000000`00000000 00000000`00000000
#  1abd30 00000000`00000000 00000000`00000000
#  1abd40 00000000`00000000 00000000`00000000
#  1abd50 00000000`00000000 00000000`00000000
#  1abd60 00000000`00000000 00000000`00000000
#  1abd70 00000000`00000000 00000000`00000000



//根据规范取出 00000000`00125863中的40位 也就是51到12位 0x0000000125000然后计算出
 

//PDPTE = 00000000`00237863
1: kd> !dq 0x0000000125000+0x7*8
#  125038 00000000`00237863 00000000`00243863
#  125048 00000000`00000000 00000000`00000000
#  125058 00000000`00000000 00000000`00000000
#  125068 00000000`00000000 00000000`00000000
#  125078 00000000`00000000 00000000`00000000
#  125088 00000000`00000000 00000000`00000000
#  125098 00000000`00000000 00000000`00000000
#  1250a8 00000000`00000000 00000000`00000000



//得到 PDPTE = 00000000`00237863，这时候我们需要查看ps是否启用了1G大小分页
//ps是第7位这里显然为0 ，我可以继续下一步提取PDE 即提取51位到12位得到 0x0000000237000
//PDE= 00000000`00325863
1: kd>  !dq 0x0000000237000+0x1F7 *0x8
#  237fb8 00000000`00325863 00000000`0014a863
#  237fc8 00000000`7a6c5863 00000000`7a6c6863
#  237fd8 00000000`7bfc4863 00000000`024d1863
#  237fe8 00000000`013a5863 00000000`03f79863
#  237ff8 00000000`0550c863 80000000`0023a963
#  238008 80000000`6e450963 80000000`04049963
#  238018 80000000`7ae2b963 80000000`7a7b2963
#  238028 80000000`7a828963 80000000`7a75a963


//   首先要判断是否是4k分页还2M分页 也就是看第7位为1（为1开启2M）
// 这里得到结论为0 所以为4k分页, 提取PTE即提取51位到12位得到 0x0000004e5f000得到物理地址


//PTE=80000000`04e5f963
1: kd> !dq 0000000325000+ 69*8
#  325348 80000000`04e5f963 80000000`04e60963
#  325358 80000000`04e61963 80000000`04e62963
#  325368 80000000`04e63963 80000000`04e64963
#  325378 80000000`04e65963 80000000`04e66963
#  325388 80000000`04e67963 80000000`04e68963
#  325398 80000000`05069963 80000000`0516a963
#  3253a8 80000000`0516b963 80000000`0026c963
#  3253b8 80000000`0016d963 80000000`0036e963

// 0x0000004e5f000加上偏移0x840得到最后的物理地址
1: kd> !dq 0000004e5f000+840
# 4e5f840 00000000`00000000 00000000`00000000
# 4e5f850 00209b00`00000000 00409300`00000000
# 4e5f860 00cffb00`0000ffff 00cff300`0000ffff
# 4e5f870 0020fb00`00000000 00000000`00000000
# 4e5f880 fe008be6`2ac00067 00000000`ffffd001
# 4e5f890 7240f36e`90007c00 00000000`00000000
# 4e5f8a0 00000000`00000000 00000000`00000000
# 4e5f8b0 ecdd8e00`00106100 00000000`fffff800

最后用两个命令分别查看物理地址和虚拟地址内存数值判断是否正确

//使用dq直接看虚拟地址内存
1: kd> dq gdtr
ffffd001`fee69840  00000000`00000000 00000000`00000000
ffffd001`fee69850  00209b00`00000000 00409300`00000000
ffffd001`fee69860  00cffb00`0000ffff 00cff300`0000ffff
ffffd001`fee69870  0020fb00`00000000 00000000`00000000
ffffd001`fee69880  fe008be6`2ac00067 00000000`ffffd001
ffffd001`fee69890  7240f36e`90007c00 00000000`00000000
ffffd001`fee698a0  00000000`00000000 00000000`00000000
ffffd001`fee698b0  ecdd8e00`00106100 00000000`fffff800
//使用!dq查看物理地址
1: kd> !dq 0000004e5f000+840
# 4e5f840 00000000`00000000 00000000`00000000
# 4e5f850 00209b00`00000000 00409300`00000000
# 4e5f860 00cffb00`0000ffff 00cff300`0000ffff
# 4e5f870 0020fb00`00000000 00000000`00000000
# 4e5f880 fe008be6`2ac00067 00000000`ffffd001
# 4e5f890 7240f36e`90007c00 00000000`00000000
# 4e5f8a0 00000000`00000000 00000000`00000000
# 4e5f8b0 ecdd8e00`00106100 00000000`fffff800