动态规划
动态规划算法与分治法类似,其基本思想也是将待求解问题分成若干个子问题。但是经分解得到的子问题往往不是互相独立的。在用分治法求解时,有些子问题被重复计算机了许多次。
如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。
与分治法的区别:
适用于动态规划算法求解的问题,经分解得到的子问题往往不是互相独立的;若用分治法求解,则分解得到的子问题数目太多,导致最终解决原问题需指数时间。
原因在于:虽然子问题的数目常常只有多项式量级,但在用分治法求解时,有些子问题被重复计算了许多次。
动态规划的基本思路:构造一张表来记录所有已解决的子问题的答案(无论算法形式如何,其填表格式是相同的)
动态规划算法的基本步骤:
- 找出最优解的性质(分析其结构特征)。
- 递归地定义最优值(优化目标函数)。
- 以自底向上的方式计算出最优值。
- 根据计算最优值时得到的信息,构造最优解。
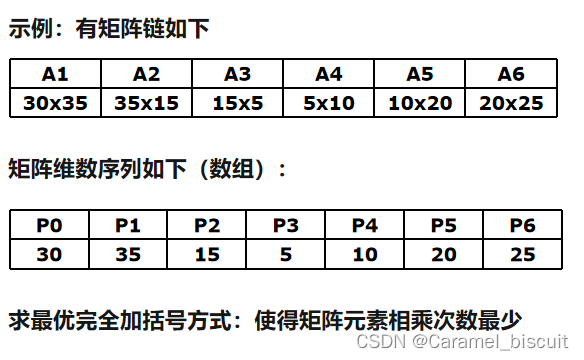
矩阵连乘问题
标准解法,设A是pxq的矩阵,B是qxr的矩阵,数乘次数为pxqxr,算法时间复杂度为0(n3)
void matrixMultiply(int **Ma,int **Mb,int **Mc,int ra,int ca,int rb,int cb){
if(ca!=rb) error("矩阵不可乘");
for(int i=0; i<ra; i++){
for(int j=0;j<cb;j++){
Mc[i][j] = 0;
for(int k=0;k<ca;k++){
Mc[i][j] += Ma[i][k] * Mb[k][j];
}
}
}
}
通过加括号的方式确定矩阵连乘问题的计算次序
- 单个矩阵是完全加括号的。
- 矩阵连乘积是完全加括号的。

应用动态规划,首先应分析问题的最优解结构特征,将矩阵连乘积(Ai…Aj)记为A[i][j],考虑A[1][n]的最优计算次序:
- 设最优计算次序在Ak和Ak+1之间将矩阵链断开。
- 则相应的完全加括号方式为(A1…Ak)(Ak+1…An)
- 总计算为以下三部分计算量之和:求解A[1:K]的计算量,求解A[k+1:n]的计算量,求解A[1:k]和A[k+1:n]相乘的计算量。
分析最优解的结构:A[1:n]的一个最优计算次序所包含的矩阵子链也是最优的,即A[1:k]和A[k+1:n]的计算次序也是最优的
建立递归关系,递归地定义最优值。
- 设:计算A[i:j]所需的最少数乘次数为m[i][j],则原问题的最优值为m[1][n]。
- 当i=j时,m[i][j]=0
- 当i<j时,可利用最优子结构性质来计算m[i][j],设Ai的维度为Pi-1xPi,假设A[i:j]的最优划分位置为k,则m[i][j]=m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j],k的取值只有j-i个,即k∈{i,i+1,…,j-1},k是使其中计算量达到最小的位置,因此m[i][j]可定义为:
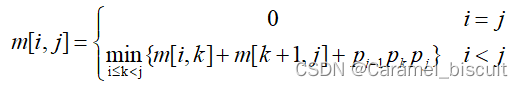
计算最优值:简单地递归
第四步:构造最优解对应的问题解值,需设置另一张表s:在填充表m的过程中,记录各个子链取最优值时的分隔位置k
- S[i][j]=k表示:A[i:j]的最优划分方式是(A[i:k])(A[k+1:j])。
- 从s[1][n]记录的信息可以知道A[1:n]的最优划分方式
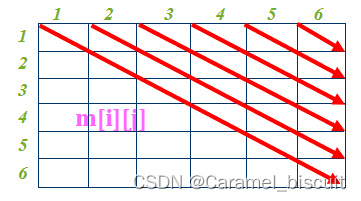
初始化是将m[i][i],即对角线初始化为0,最顶层是m[1][n]
数据结构
- 形参表中应有n和P[n+1]。
- 算法需要两个二维数组m[n][n]。其每个元素m[i][j]为A[i:j]的最少数乘次数,二维矩阵s[n][n],其元素为断点位置。
void matrixChain(int *p,int n,int **m,int **s){
for(int i=1; i<=n; i++) m[i][i]=0;
for(int r=2; r<=n; r++){ //链长
for(int i=1; i<=n-r+1; i++){
int j = i+r-1;
m[i][j] = m[i][i] + m[i+1][j] + p[i-1]*p[i]*p[j];
s[i][j] = i;
for(int k=i+1; k<n;k++){
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if(t < m[i][j]){
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
算法复杂度分析:matrixChain的主要计算量取决于算法中对r,i和k的三重循环,因此算法的计算时间上界为O(n3),算法所占用的空间为O(n2)
动态规划算法的基本要素
最优子结构
矩阵连乘的计算次序问题具有最优子结构性质——矩阵连乘计算次序问题的最优解包含着其子问题的最优解。
在分析问题的最优子结构性质,所用的方法具有普遍性:
- 首先假设由问题的最优解导出的子问题的解不是最优的
- 然后设法证明在该假设下可构造出比原问题最优解更好的解
- 通过矛盾法证明由最优解导出的子问题的解也是最优的
解题方法:利用问题的最优子结构性质,以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。
最优子结构是问题能用动态规划算法求解的前提,同一个问题可以有多种方式刻画它的最优子结构,有些表示方法的求解速度更快。(空间占用小,问题的维度低)
重叠子问题
采用递归算法求解问题时,产生的子问题并不总是独立的。有些子问题被反复计算多次,称为子问题的重叠性质。
备忘录方法
备忘录方法是动态规划算法的一种变形,它也用表格来保存已解决的子问题答案,以避免重复计算。
与动态规划的区别在于备忘录方法是自顶向下的递归。
备忘录方法的控制结构与直接递归方法的控制结构相同。
- 区别在于备忘录方法为每个解过的子问题建立了备忘录。
- 以备需要时查看,从而避免了相同子问题的重复求解。
算法时间复杂度O(n3),算法空间复杂度为O(n2)。
int MemorizedMatrixChain(int n,int **m,int **s){
for(int i=1; i<=n; i++)
for(int j=i; j<=n; j++)
m[i][j] = 0;
return LookupChain(1,n);
}
int LookupChain(int i,int j){
if(m[i][j] > 0) return m[i][j];
if(i == j)
return 0;
int u = LookupChain(i,i) + LookupChain(i+1,j) + p[i-1]*p[i]*p[j];
s[i][j] = i;
for(int k=i+1; k<j; k++){
int t = LookupChain(i,k) + LookupChain(k+1,j) + p[i-1]*p[k]*p[j];
if(t < u){
u = t;
s[i][j] = k;
}
}
m[i][j] = u;
return u;
}
最长公共子序列问题(Longest Common Subsequence)
子序列和子串
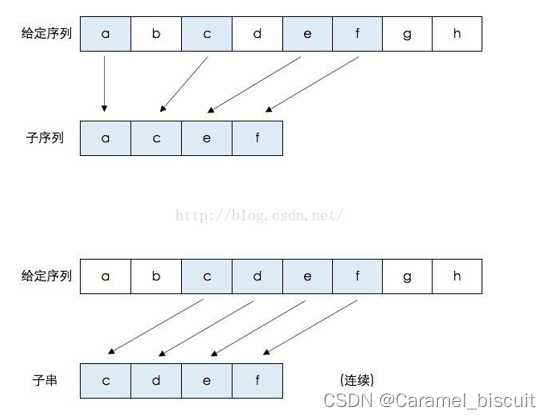
最长公共子序列问题具有最优子结构性质
给定序列X={x1, x2, ……, xm} 和 Y={y1, y2, ……, yn},设它们的一个最长公共子序列为Z={z1, z2,…, zk} ,则:
- 若xm = yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的LCS
- 若xm!=yn且zk!=xm,则Z是Xm-1和Y的LCS
- 若xm!=yn且zk!=yn,则Z是X和Yn-1的LCS
可见LCS(X,Y)包含了X和Y这2个序列的前缀子序列的LCS,因此最长公共子序列问题具有最优子结构性质。
假如S1的最后一个元素与S2的最后一个元素不相等,那么S1和S2的最长公共子序列等于:{S1减去最后一个元素}与S2的最长公共子序列,{S2减去最后一个元素}与S1的LCS中的最大的那个序列。
建立递归关系,用c[i][j]表示序列Xi和Yj的最长公共子序列的长度。
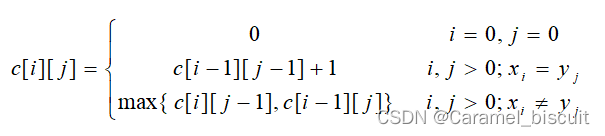
如果直接用递归算法求解递归式,则时间随输入规模成指数增长。
设置两个数组作为输出:
- c[i][j]表示序列Xi和Yj的最长公共子序列的长度,问题的最优值记为c[m][n],即LCS(X,Y)的长度。
- b[i][j]记录c[i][j]是从哪一个子问题的解得到的,数组b用于构造最长公共子序列(最优解)。
void LCSLength(int m,int n,char *x,char *y,int **c,int **b){
int i,j;
for(i=1; i<=m; i++)
c[i][0] = 0;
for(j=1; j<=n; j++)
c[0][j] = 0;
for(i=1; i<=m; i++){
for(j=1; j<=n; j++){
if(x[i]==y[j]){
c[i][j] = c[i-1][j-1]+1;
b[i][j] = 1;
}else if(c[i-1][j] <= c[i][j-1]){
c[i][j] = c[i-1][j];
b[i][j] = 2;
}else{
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
}
算法时间复杂度O(mn)
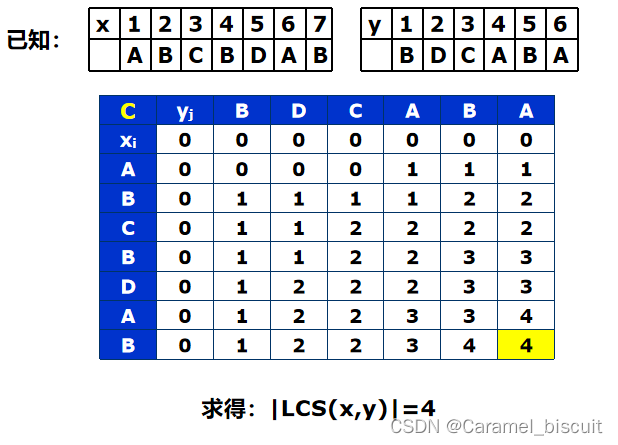
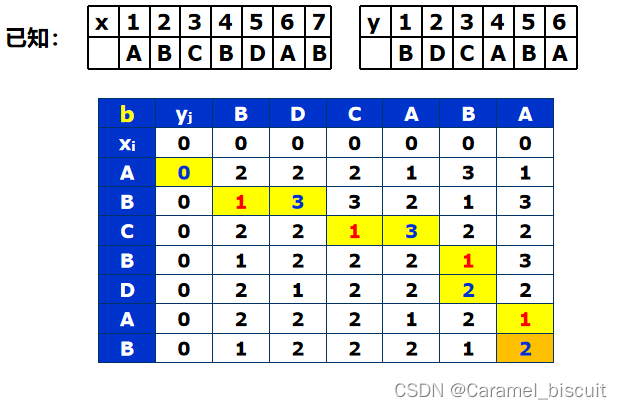
构造最长公共子序列
void LCS(int i,int j,char *x,int **b){
if(i==0||j==0)
return;
if(b[i][j]==1){
LCS(i-1,j-1,x,b);
printf("%d",x[i]);
}else if(b[i][j]==2){
LCS(i-1,j,x,b);
}else{
LCS(i,j-1,x,b);
}
}
还可以去掉数组b,只需要根据c[i][j]和每个字符串最后字符是否相等判断。
最大子段和问题(Maximum Sub-Sequence Sum)
给定n个整数(可能为负数)组成的序列a1,a2,…,an,求该序列形如下式的子段和的最大值,当所有整数均为负整数时定义其最大子段和为0。
最大子段和问题:简单算法,时间复杂度O(n2)
int MaxSum(int n,int *pa,int *besti,int *bestj){
int sum = 0;
for(int i=1; i<=n; i++){
int tmp =0;
for(int j=i; j<=n; j++){
tmp +=pa[j];
if(tmp > sum){
sum = tmp;
*besti = i;
*bestj = j;
}
}
}
}
最大子段和问题:分治算法,时间复杂度O(nlogn)
- 如果将序列a[1:n]分为等长两段:a[1:n/2]和a[n/2+1:n]
- 可以分别求出a[1:n/2]和a[n/2+1:n]的最大子段和
- 原问题的最大子段和a[1:n]有三种情形:a[1:n]的最大子段和与a[1:n/2]的最大子段相同,a[1:n]的最大子段和与a[n/2+:n]的最大子段相同,a[1:n]的最大子段和产生于跨越两段分界点的子序列——显然此时有a[n/2]和a[n/2+1]在最优子序列中,可分别求得包含a[n/2]和a[n/2+1]的极大子段和S1和S2,则a[1:n]的最大子段和=S1+S2。
int MaxSubSum(int *a,int left,int right){
int sum = 0;
if(left == right) sum=a[left]>0 ? A[left]:0;
else{
int center = (left+right)/2;
int leftSum = MaxSubSum(a,left,center);
int rightSum = MaxSubSum(a,center+1,right);
//从中向左
int s1 = 0;
int lefts = 0;
for(int i=center; i>=left;i--){
lefts+=a[i];
if(lefts > s1){
s1 = lefts;
}
}
int s2 = 0;
int rights = 0;
for(i=center+1; i<=right;i++){
rights += a[i];
if(rights > s2){
s2 = rights;
}
}
sum = s1+s2;
if(sum < leftSum){
sum = leftSum;
}
if(sum < rightSum){
sum = rightSum;
}
}
return sum;
}
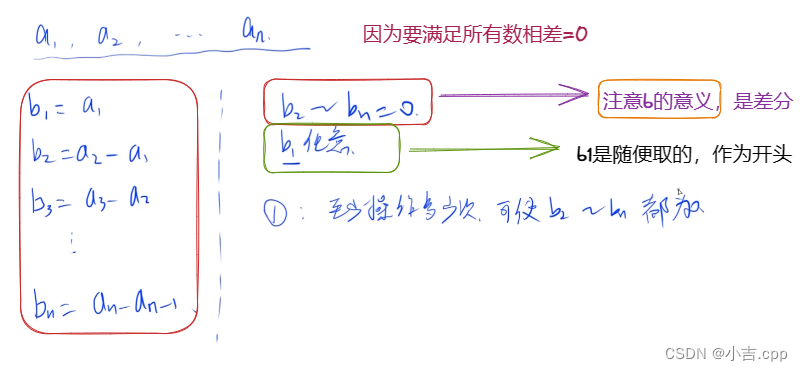
最大子段和问题:动态规划算法时间复杂度O(n)
int MaxSum(int n,int *a){
int sum = 0;
int b = 0;
for(int i=1; i<=n; i++){
if(b>0){
b+=a[i];
}else{
b = a[i];
}
if(b > sum){
sum = b;
}
}
return sum;
}
凸多边形最优三角剖分问题
当一个简单多边形及其内部构成一个闭凸集时,称为凸多边形。
凸集的含义:凸多边形边界或内部的任意两点所连成的直线段上的所有点均在凸多边形的内部或边界上。
通常用多边形顶点的逆时针序列表示凸多边形,V={v0, v1, ……, vn-1} 表示具有n条边(v0, v1),(v1, v2 ),……,(vn-1 , vn)的一个凸多边形(约定:v0 =vn )。
凸多边形的三角剖分
- 将多边形P分割成互不相交的三角形的弦的集合T。
- 在该部分中各弦互不相交,且集合T已达到最大。
在有n个顶点的凸多边形,恰有n-3条弦和n-2个三角形。
给定凸多边形P,以及定在由多边形的边和弦组成的三角形上的权函数W,要求确定该凸多边形的三角部分,使得该三角部分中诸三角形上权值之和最小。
完全加括号表达式的语法树
矩阵连乘的最优计算次序等价于矩阵链的最优完全加括号方式,一个表达式的完全加括号方式相当于一颗平衡二叉树
例如:完全加括号的矩阵连乘积((A1(A2A3))(A4(A5A6))),可以用如下的平衡二叉树进行表示,其中叶节点为表达式中的原子;树根表示左右子树相结合,这样的二叉树称为该表达式的语法树。
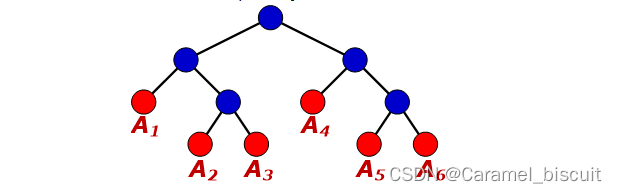
凸多边形三角剖分也可以用语法树来表示(如图)
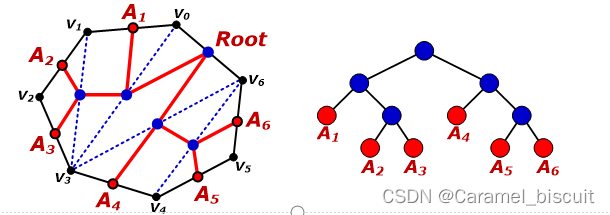
- 该语法树的根节点为边(V0,V6)
- 三角剖分中的弦组成其余的内节点(子树的根节点)
- 多边形中除(V0,V6)外的各条边都是语法树的一个叶节点。
凸多边形三角剖分与矩阵连乘问题的同构关系
- 凸n边形的三角剖分和有n-1个叶节点的语法树存在一一对应关系。
- n个矩阵的完全加括号乘积和有n个叶节点的语法树存在一一对应关系。
- 推论:n个矩阵连乘的完全加括号和凸n+1边形的三角剖分也存在一一对应关系。其中Ai对应于凸多边形的一条边(Vi-1,Vi),三角剖分中的每条弦(Vi,Vj)对应于一组矩阵的连乘积A[i+1,j]
矩阵连乘的最优计算次序问题是凸多边形最优三角剖分的特例。
- 对于给定的矩阵链(A1 A2 … An)。
- 定义一个与之相应的凸多边形P={v0,v1,…,vn}。
- 使得矩阵Ai与凸多边形的边(Vi-1,Vi)一一对应。
- 若矩阵Ai的维数为Pi-1xPi
- 定义三角形(ViVjVk)上的权函数值:w(ViVjVk)=pixpjxpk
- 则凸多边形P的最优三角剖分所对应的语法树同时也给出了该矩阵A1A2 … An 的最优完全加括号方式
凸多边形最优三角剖分的最优子结构性质
设:T为凸多边形P={v0,v1,…,vn}的一个最优三角剖分。
并设:T包含三角形v0vkvn
则:T的权为三部分权之和:三角形v0vkvn的权,以及两个子多边形{V0,…,Vk}和{Vk,…,Vn}的权之和。
可以断言:由T所确定的这两个子多边形的三角剖分也是最优的。
这是因为:若子多边形有更小权的三角剖分,则三部分之和将小于T的值,这将导致T不是最优三角剖分的矛盾。
设:t[i][j]为凸子多边形p{Vi-1,Vi,…,Vj}的最优三角剖分所对应的权函数值,即三角剖分的最优值。
设:退化的两顶点多边形{Vi-1Vi}具有权值0(t[i][i] = 0)
则:原问题(凸n+1边形)的最优权值为t[1][n]。
当(j-i)>=1时,凸子多边形{Vi-1,Vi,…,Vj}至少有三个顶点,设k为其中一个中间点(i<=k<j),由最优子结构性质,t[i][j]的值应为三部分权值之和:两个凸子多边形的最优权值t[i][k]和t[k+1][j]加上三角形Vi-1VkVj的权值。
由于K的可能位置有j-i个,因此问题转换为:在其中选择使得t[i][j]达到最小的位置,相应地得到t[i][j]递归定义如下:
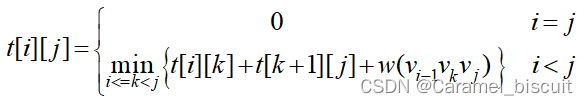
与矩阵连乘问题相比,除了权函数的定义外,t[i][j]与m[i][j]的递归式完全相同,因此只需对MatrixChain算法做少量修改即可。
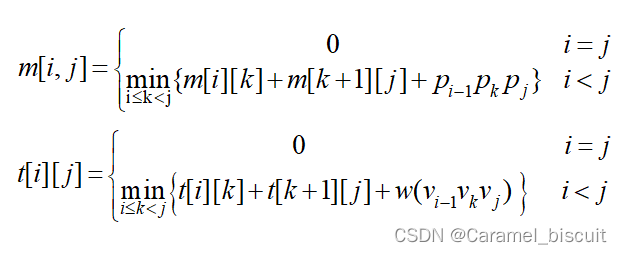
void minweighttriangulation(int n,int **t,int **s){
for(int i=1; i<=n; i++) t[i][i] = 0;
for(int r=2; r<=n; r++){
for(int i=1; i<=n-r+1; i++){
int j = i+r-1;
t[i][j] = t[i+1][j] + w(i-1,i,j);
s[i][j] = i;
for(int k=i+1; k<n; k++){
int u = t[i][k] + t[k+1][j] + w(i-1,k,j);
if(u < t[i][j]){
t[i][j] = u;
s[i][j] = k;
}
}
}
}
}
与矩阵连乘算法的复杂度一样,计算时间上界为O(n3),算法所占用的空间为O(n2)。
凸多边形最优三角剖分的最优解
- 计算最优值t[1][n]时,可以用数组S记录三角剖分信息。
- S[i][j]记录于(Vi-1,Vj)共同组成三角形的第三个顶点的位置。
图像压缩问题
灰度图
灰度图是指用灰度表示的图像,灰度是在白色和黑色之间分的若干个等级,其中最常用的是256级,也就是256级灰度图,灰度就是没有色彩,RGB色彩分量全部相等。
例如:RGB(100,100,100) 代表灰度为100
例如:RGB(50,50,50) 代表灰度为50
在计算机中常用像素点的灰度值序列来表示图像
**灰度图的压缩:**图像A的像素点灰度值序列为:{p1,p2,…pn},整数值pi (0 ≤ pi ≤ n) 表示像素点 i 的灰度值,像素点灰度值取值范围[0-255],表示为8位二进制数,减少表示像素点的位数,可以降低图像的空间占用需求。
设:P = {10,12,15,255,1,2,1,1,2,2,1,1}
- S1 = {10, 12, 15, 255, 1, 2, 1, 1, 2, 2, 1, 1}
- 分成12个组,每组仅包含一个像素
- S1 = {10, 12, 15} S2 = {255} S3 = {1, 2, 1, 1, 2, 2, 1, 1}
所需存储空间
分法1:8×12 + 11×1 = 107
分法2:4×3 + 8×1 + 1×5 + 2×3 + 11×12 = 163
分法3:4×3 + 8×1 + 2×8 + 11×3 = 69
0/1背包问题
证明0/1背包是最优子结构(反证)
设(x1,x2,…,xn)是所给0/1背包问题的一个最优解,则(x2,…,xn)是下面一个子问题的最优解:
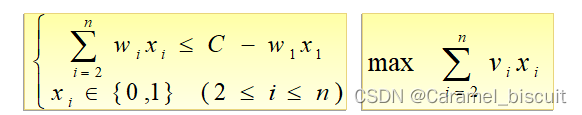
如若不然,设(y2,…,yn)是上述问题的一个最优解,则
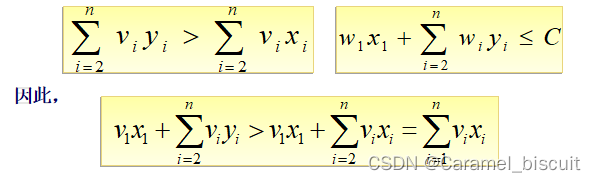
这说明(x1,y2,…,yn)是所给0/1背包问题比(x1,x2,…,xn)更优的解,从而导致矛盾。
令V(i,j)表示前i个物品中能够装入容量为j的背包中的物品的最大价值。
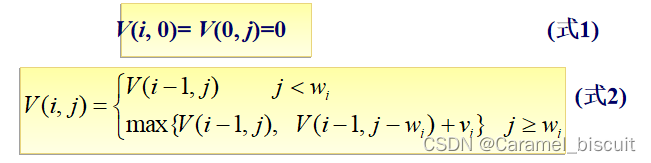
- 把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包,得到的价值均为0。
- 如果第i个物品的重量大于背包的容量,则物品i不能装入背包,则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的。
- 如果第i个物品的重量小于背包的容量,就会有两种情况:如果第i个物品没有装入背包,则背包中物品的价值就等于前i-1个物品装入容量为j的背包中所取得的价值。
- 如果第i个物品装入背包,则背包中物品的价值等于前i-1个物品装入容量为j-w[i]的背包中的价值加上第i个物品的价值vi。
- 取二者中价值较大者作为前i个物品装入容量为j的背包中的最优解。
设n个物品的重量存储在数组w[n]中,价值存储在v[n]中,背包容量C,数组V[n+1][C+1]存放迭代结果,其中V[i][j]表示前i个物品装入容量为j的背包中获得的最大价值,数组x[n]存储装入背包的物品,动态规划法求解0/1背包问题:
int KnapSack(int n,int w[],int v[]){
for(int i=0; i<=n; i++)
V[i][0] = 0;
for(int i=0; i<=C; i++)
V[0][i] = 0;
for(int i=1; i<=n; i++){
for(int j=1; j<=C; j++){
if(w[i] > j){
V[i][j] = V[i-1][j];
}else{
if(V[i-1][j-w[i]]+v[i] >= V[i-1][j]){
V[i][j] = V[i-1][j-w[i]] + v[i];
}else{
V[i][j] = V[i-1][j];
}
}
}
}
// 求装入背包的物品
j = C;
for(i=n;i>0;i--){
if(V[i][j]>V[i-1][j]){
x[i] = 1;
j = j-w[i];
}else{
x[i] = 0;
}
}
return V[n][C];
}
算法时间复杂度为O(nxC)
最优二叉查找树(Optimal Binary Search Tree)
二叉查找树
- 设S={k1,k2,…,kn}是n个互异的关键字组成的有序集,且k1<k2<…<kn。
- 可利用二叉树的节点存储有序集S中的元素,称为二叉查找树。
二叉查找树的性质
- 二叉查找树中任意节点:大于其左子树中任意节点;小于等于其右子树中任意节点。
- 二叉查找树的叶节点是形如(ki,ki+1)的开区间,以符号di表示虚拟的叶节点,约定d0=-无穷,dn+1=正无穷
- 在二叉查找树中搜索一个元素k,返回的结果有两种情况,在二叉查找树的内节点中找到ki==k,在二叉查找树的叶节点中确定k ∈ (ki, ki+1)
二叉搜索树的搜索代价:已知了每个关键字和虚拟键被搜索的概率,可以确定在给定二叉搜索树T内一次搜索的期望代价。假设一次搜索的实际代价为检查的结点的个数,在T内搜索所发现的“结点的深度”加“1”。
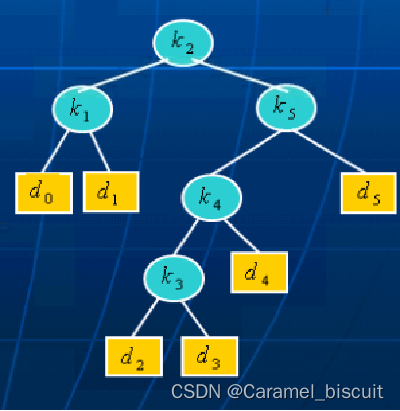
k3的结点深度为3,要找到结点k3,需要检查3+1=4个结点的个数k2 k5 k4 k3。
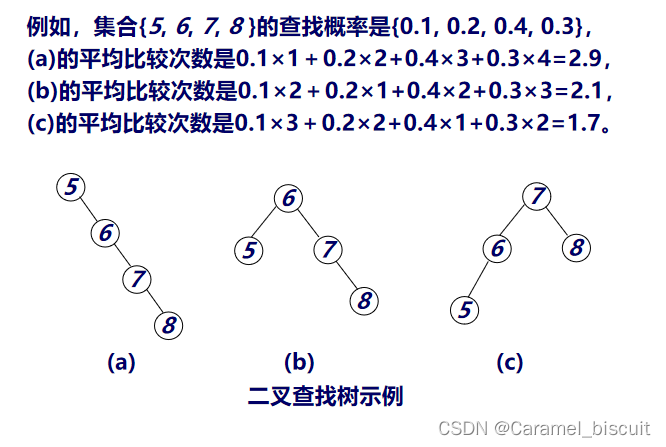
证明最优二叉查找树满足最优性原理
将由{r1,r2,…,rn}构成的二叉查找树记为T(1,n),其中rk(1≤k≤n)是T(1,n)的根节点,则其左子树T(1,k-1)由{r1,…,rk-1}构成,其右子树T(k+1,n)由{rk+1,…,rn}构成。
若T(1,n)是最优二叉查找树,则其左子树T(1,k-1)和右子树T(k+1,n)也是最优二叉查找树,如若不然,假设S(1,k-1)是比T(1,k-1)更优的二叉查找树,则S(1,k-1)的平均比较次数小于T(1,k-1)的平均比较次数,从而由S(1,k-1),rk,T(k+1,n)构成的二叉查找树S(1,n)的平均比较次数小于T(1,n)的平均比较次数,这与T(1,n)是最优二叉查找树的假设矛盾。
最优子结构分析
对于给定关键字序列{ki,…,kj},假设kr是包含该序列的一棵最优子树的根,根kr的左子树包含ki,…kr-1,根kr的右子树包含kr+1,…kj。
- 依次检查所有的侯选根(设为kr)。
- 确定包含关键字ki,…kr-1和kr+1,…,kj的所有二叉查找树。
- 其中期望搜索代价最小就是最优二叉查找树。
- 问题的关键:确认“权重”函数(子树的期望代价)
钢条切割问题
某公司出售一段长度为i英寸的钢条的价格为p[i](i=1,2,3,…),钢条长度整英寸如图:

现在先给一段长度为n的钢条,问怎么切割,获得的收益最大rn?
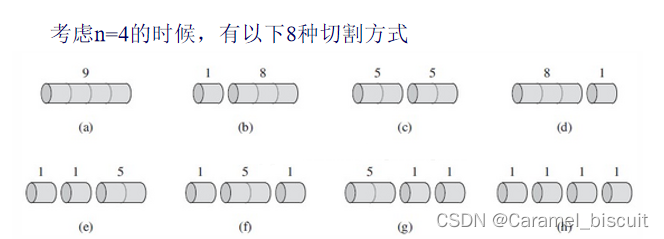
假如一个最优解把n段切成了k段(1≤k≤n),那么最优切割方案:n=i[1]+i[2]+…+i[k],最大收益:rn=p[i[1]]+p[i[2]]
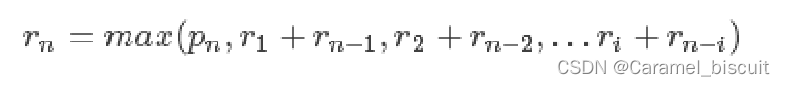
第一个参数Pn为不切割方案,其它n-1个参数对应n-1种方案:对于每个i=1,2,…,n-1,首先把钢条分为长度为i和n-i的两端钢条,分别求出这两段钢条的最优ri和rn-i(每种方案的最优收益为两段的最优收益之和)。
生产与存储问题
某工厂每月需供应市场一定数量的产品。供应需求所剩余产品应存入仓库,一般地说,某月适当增加产量可降低生产成本,但超产部分存入仓库会增加库存费用,要确定一个每月的生产计划,在满足需求条件下,使一年的生产与存储费用之和最小。
投资决策问题
某公司现有资金Q亿元,在今后5年内考虑给A、B、C、D四个项目投资,这些项目的投资期限、回报率均不相同,问应如何确定这些项目每年的投资额,使到第五年末拥有资金的本利总额最大。
设备更新问题
企业使用设备都要考虑设备的更新问题,因为设备越陈旧所需的维修费用越多,但购买新设备则要一次性支出较大的费用。现在某企业要决定一台设备未来8年的更新计划,已预测到第j年购买设备的价格为Kj,Gj为设备经过j年后的残值,Cj为设备连续使用j-1年后在第j年的维修费用(j=1,2…8),问应在哪年更新设备可使总费用最小

![【开发规范】go项目开发中的[流程,git,代码,目录,微服务仓库管理,静态检查]](https://img-blog.csdnimg.cn/e3ed8135e2e14fa58027c416b942ffce.png#pic_center)