👨‍💻作者简介： 大数据专业硕士在读，CSDN人工智能领域博客专家，阿里云专家博主，专注大数据与人工智能知识分享。
🎉专栏推荐： 目前在写CV方向专栏，更新不限于目标检测、OCR、图像分类、图像分割等方向，目前活动仅19.9，虽然付费但会长期更新，感兴趣的小伙伴可以关注下➡️专栏地址
🎉学习者福利： 强烈推荐一个优秀AI学习网站，包括机器学习、深度学习等理论与实战教程，非常适合AI学习者。➡️网站链接。
🎉技术控福利：程序员兼职社区招募！靠谱覆盖技术范围广，CV、NLP均可，Pyhton、matlab各类编程语言, 有意向者➡️访问。

---

📝导读：本篇为注意力机制系列第二篇，主要介绍注意力机制中的通道注意力机制，对通道注意力机制方法进行详细讲解，会对重点论文会进行标注 * ，并配上论文地址和对应代码。
🆙 注意力机制详解系列目录：

1️⃣注意力机制详解系列（一）：注意力机制概述
2️⃣注意力机制详解系列（二）：通道注意力机制
3️⃣注意力机制详解系列（三）：空间注意力机制（待更新）
4️⃣注意力机制详解系列（四）：混合与时域注意力机制（待更新）
5️⃣注意力机制详解系列（五）：注意力机制总结（待更新）

1.通道注意力机制

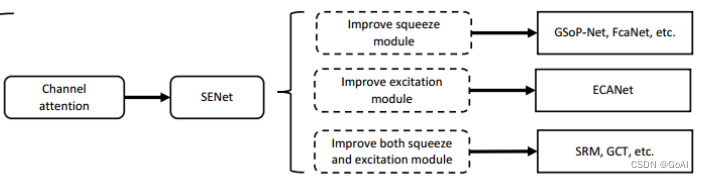
通道注意力机制模型总结

通道注意力机制在计算机视觉中，更关注特征图中channel之间的关系，而普通的卷积会对通道做通道融合，这个开山鼻祖是SENet,后面有GSoP-Net，FcaNet 对SENet中的squeeze部分改进，EACNet对SENet中的excitation部分改进，SRM,GCT等对SENet中的scale部分改进。

通道注意力机制模型对比：

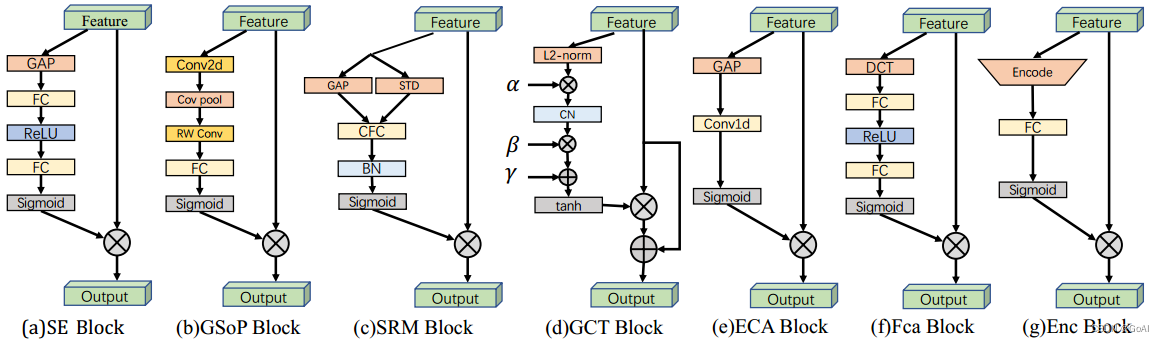
对应论文链接：

论文缩写	论文名称 | 链接	权重范围	论文投稿
SE Block	Squeeze-and-Excitation Networks	(0,1)	CVPR2018
GSoP Block	Global Second-order Pooling Convolutional Networks	(0,1)	CVPR2019
SRM Block	SRM : A Style-based Recalibration Module for Convolutional Neural Networks	(0,1)	ICCV2019
GCT Block	Gated Channel Transformation for Visual Recognition	(0,1)	CVPR2020
ECA Block	ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks	(0,1)	CVPR2020
Fca Block	FcaNet: Frequency Channel Attention Networks	(0,1)	ICCV2021
Enc Block	Context Encoding for Semantic Segmentation	(-1,1)	CVPR2018

1.SENet

论文：https://arxiv.org/abs/1709.01507
Github：https://github.com/hujie-frank/SENet
https://github.com/moskomule/senet.pytorch

SENet是CVPR17年的一篇文章提出。在卷积神经网络中，卷积操作更多的是关注感受野，在通道上默认为是所有通道的融合（深度可分离卷积不对通道进行融合，但是没有学习通道之间的关系，其主要目的是为了减少计算量），SENet提出SE模块，通过学习的方式自动获取每个特征通道的重要程度，学习到不同通道之间的权重,并且利用得到的重要程度来提升特征并抑制对当前任务不重要的特征。

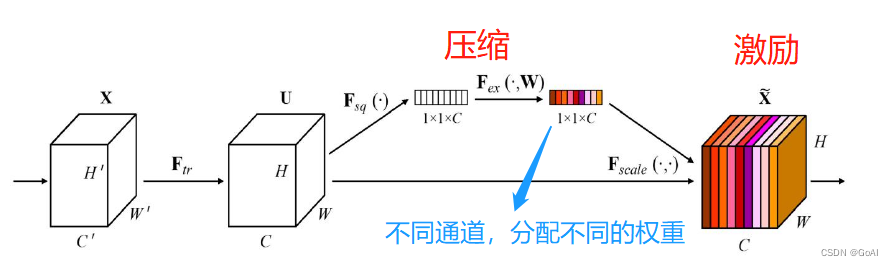
SE模块主要由三部分组成：squeeze、excitation和scale。实现步骤如下：

总体概述：

（1）Squeeze：通过全局平均池化，将每个通道的二维特征（H*W）压缩为1个实数，将特征图从 [h, w, c] ==> [1,1,c]

（2）excitation：给每个特征通道生成一个权重值，论文中通过两个全连接层构建通道间的相关性，输出的权重值数目和输入特征图的通道数相同。[1,1,c] ==> [1,1,c]

（3）Scale：将前面得到的归一化权重加权到每个通道的特征上。论文中使用的是乘法，逐通道乘以权重系数。[h,w,c]*[1,1,c] ==> [h,w,c]

在这种方式下，每一个样本，都会有自己独立的一组权重。换言之，任意的两个样本，它们的权重，都是不一样的。在SENet中，获得权重的具体路径是，“全局池化→全连接层→ReLU函数→全连接层→Sigmoid函数”。

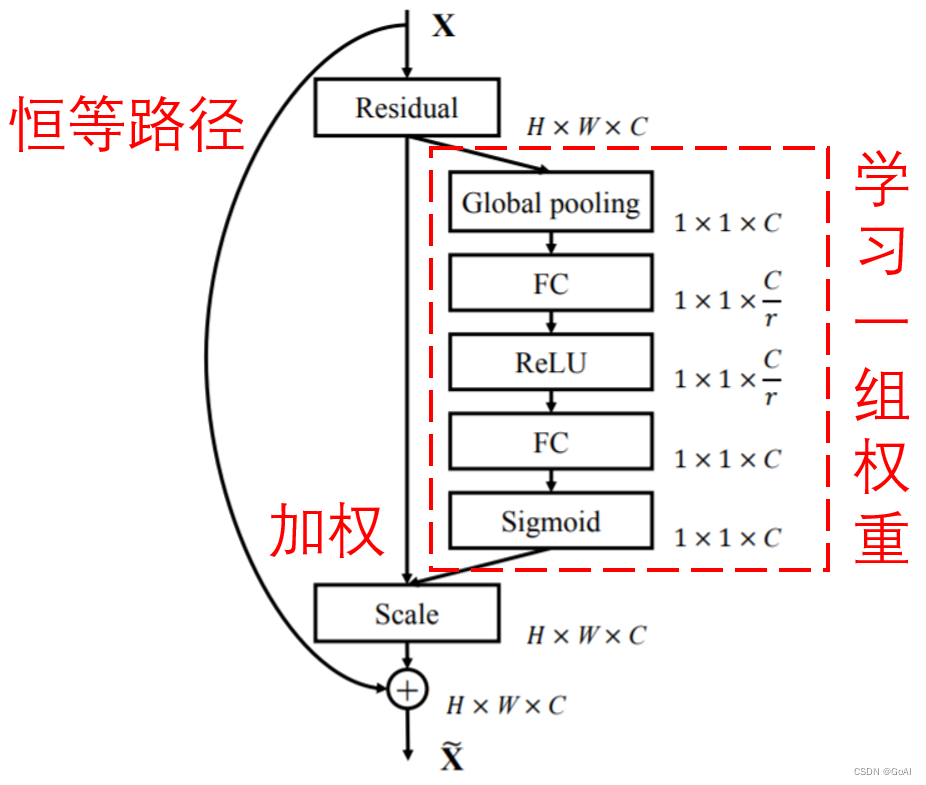
详细解释：

第一步首先对h* w* c大小的feature map 做squeeze操作将其变成1 * 1 * c大小，这一步原文中使用简单粗暴的GAP(全局平均池化)；

第二步excitation操作，对1 * 1 * c的特征图经过两次全连接，特征图大小1 * 1 * c→1 * 1 * 3→1* 1 * c，再对1 * 1* c的特征图做sigmoid将值限制到[0,1]范围内；

第三步scale,将1 * 1 * c的特征权重图与输入的h * w * c的feature map在通道上相乘；完成SE模块的通道注意力机制。

值得注意的是，在squeeze部分，作者使用的是最简单的全局平均池化的方式，主要原因是作者基于通道的整体信息，关注通道之间的相关性，而不是空间分布的相关性，也尽可能的屏蔽掉空间分布信息；在excitation部分，作者通过两个全连接实现1 * 1 * c2→1 * 1 * c3→1 * 1 * c2，第一个全连接层将c2压缩到c3，用于计算量减少，在原文中作者做实验后发现c3=c2/16时，能实现性能和计算量的平衡。

SE模型同Inception，可以即插即用，理论上可以安插在任意一个卷积后面，简单方便，只会增加一点参数量和计算量。

SENet的实现代码如下：

class SELayer(nn.Module):
    def __init__(self, channel, reduction=1):
        super(SELayer, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc1 = nn.Sequential(
            nn.Linear(channel, channel / reduction),
            nn.ReLU(inplace=True),
            nn.Linear(channel / reduction, channel),
            nn.Sigmoid())
        self.fc2 = nn.Sequential(
            nn.Conv2d(channel , channel / reduction, 1, bias=False)
            nn.ReLU(inplace=True),
            nn.Conv2d(channel / reduction, channel, 1, bias=False)
            nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc1(y).view(b, c, 1, 1)
        return x * y

SE模块插入Resnet代码：

class SEBottleneck(nn.Module):
        expansion = 4
 
        def __init__(self, inplanes, planes, stride=1, downsample=None, reduction=16):
            super(SEBottleneck, self).__init__()
            self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=1, bias=False)
            self.bn1 = nn.BatchNorm2d(planes)
            self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=stride,
                                   padding=1, bias=False)
            self.bn2 = nn.BatchNorm2d(planes)
            self.conv3 = nn.Conv2d(planes, planes * 4, kernel_size=1, bias=False)
            self.bn3 = nn.BatchNorm2d(planes * 4)
            self.relu = nn.ReLU(inplace=True)
            self.se = SELayer(planes * 4, reduction)
            self.downsample = downsample
            self.stride = stride
 
        def forward(self, x):
            residual = x
 
            out = self.conv1(x)
            out = self.bn1(out)
            out = self.relu(out)
 
            out = self.conv2(out)
            out = self.bn2(out)
            out = self.relu(out)
 
            out = self.conv3(out)
            out = self.bn3(out)
            out = self.se(out)
 
            if self.downsample is not None:
                residual = self.downsample(x)
 
            out += residual
            out = self.relu(out)
 
            return out

GSoP-Net

论文：https://arxiv.org/abs/1811.12006

github:https://github.com/ZilinGao/Global-Second-order-Pooling-Convolutional-Networks

SE模块中squeeze部分用的是全局平均池化，GSoP-Net的主要创新点是将一阶全局平均池化替换成二阶池化，主要操作为对输入为hwc‘的特征图先通过卷积降维到hwc,然后通道之间两两计算相关性，得到cc的协方差矩阵，第i行元素表明第i i个通道和其他通道的统计层面的依赖。由于二次运算涉及到改变数据的顺序，因此对协方差矩阵执行逐行归一化，保留固有的结构信息。然后通过激励模块对协方差特征图做非线性逐行卷积得到11*4c的特征信息，后面同SENet。相对于SNet,增加了全局的统计建模。

FcaNet

论文：http://arxiv.org/abs/2012.11879

github: https://github.com/cfzd/FcaNet

FCANet主要也是更新SE模块中squeeze部分，作者设计了一种新的高效多谱通道注意力框架。该框架在GAP是DCT的一种特殊形式的基础上，在频域上推广了GAP通道注意力机制，提出使用有限制的多个频率分量代替只有最低频的GAP。通过集成更多频率分量，不同的信息被提取从而形成一个多谱描述。此外，为了更好进行分量选择，作者设计了一种二阶段特征选择准则，在该准则的帮助下，提出的多谱通道注意力框架达到了SOTA效果。

ECA-Net

论文: https://arxiv.org/pdf/1910.03151

代码: https://github.com/BangguWu/ECANet

ECANet介绍：

ECANet主要对SENet模块进行了一些改进，提出了一种不降维的局部跨信道交互策略（ECA模块）和自适应选择一维卷积核大小的方法，使得通道数较大的层可以更多地进行跨通道交互，从而实现了性能上的提优。

ECANet主要对SENet中的excitation部分改进，SENet采用的降维操作会对通道注意力的预测产生负面影响，且获取依赖关系效率低且不必要，因此提出了一种针对CNN的高效通道注意力(ECA)模块，避免了降维，有效地实现了跨通道交互。

ECANet通过大小为 k 的快速一维卷积实现，其中核大小k表示局部跨通道交互的覆盖范围，即有多少领域参与了一个通道的注意预测 ；同时为了避免通过交叉验证手动调整 k，开发了一种自适应方法确定 k，其中跨通道交互的覆盖范围 (即核大小k) 与通道维度成比例 。

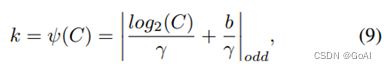
这里 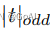表示最近的奇数t。本文中将γ设置为2，b设置为1。

ECANet实现流程：

（1）将输入特征图经过全局平均池化，特征图从 [h,w,c] 的矩阵变成 [1,1,c] 的向量

（2）根据特征图的通道数计算得到自适应的一维卷积核大小 kernel_size

（3）将 kernel_size 用于一维卷积中，得到对于特征图的每个通道的权重

（4）将归一化权重和原输入特征图逐通道相乘，生成加权后的特征图

核心：ECA 注意力机制模块直接在全局平均池化层之后使用1x1卷积层，去除了全连接层。该模块避免了维度缩减，并有效捕获了跨通道交互。并且ECANet 只涉及少数参数就能达到很好的效果。

ECANet实战代码：

#ECANet使用1D卷积代替SE注意力机制中的全连接层
import torch
from torch import nn
import math
from torchstat import stat  # 查看网络参数
 
# 定义ECANet的类
class eca_block(nn.Module):
    # 初始化, in_channel代表特征图的输入通道数, b和gama代表公式中的两个系数
    def __init__(self, in_channel, b=1, gama=2):
        # 继承父类初始化
        super(eca_block, self).__init__()
        
        # 根据输入通道数自适应调整卷积核大小
        kernel_size = int(abs((math.log(in_channel, 2)+b)/gama))
        # 如果卷积核大小是奇数，就使用它
        if kernel_size % 2:
            kernel_size = kernel_size
        # 如果卷积核大小是偶数，就把它变成奇数
        else:
            kernel_size = kernel_size
        
        # 卷积时，为例保证卷积前后的size不变，需要0填充的数量
        padding = kernel_size // 2
        
        # 全局平均池化，输出的特征图的宽高=1
        self.avg_pool = nn.AdaptiveAvgPool2d(output_size=1)
        # 1D卷积，输入和输出通道数都=1，卷积核大小是自适应的
        self.conv = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=kernel_size,
                              bias=False, padding=padding)
        # sigmoid激活函数，权值归一化
        self.sigmoid = nn.Sigmoid()
    
    # 前向传播
    def forward(self, inputs):
        # 获得输入图像的shape
        b, c, h, w = inputs.shape
        
        # 全局平均池化 [b,c,h,w]==>[b,c,1,1]
        x = self.avg_pool(inputs)
        # 维度调整，变成序列形式 [b,c,1,1]==>[b,1,c]
        x = x.view([b,1,c])
        # 1D卷积 [b,1,c]==>[b,1,c]
        x = self.conv(x)
        # 权值归一化
        x = self.sigmoid(x)
        # 维度调整 [b,1,c]==>[b,c,1,1]
        x = x.view([b,c,1,1])
        
        # 将输入特征图和通道权重相乘[b,c,h,w]*[b,c,1,1]==>[b,c,h,w]
        outputs = x * inputs
        return outputs

SRM

论文: https://arxiv.org/pdf/1903.10829

代码:https://github.com/hyunjaelee410/style-based-recalibration-module

SRM受风格迁移的启发，对SENet中的squeeze和excitation部分进行更新：

提出了一种基于style的重新校准模块（SRM)，可以通过利用其style自适应地重新校准中间特征图。SRM首先通过样式池从特征图的每个通道中提取样式信息，然后通过与通道无关的style集成来估计每个通道的重新校准权重。

给定一个输入特征特征图大小为C × H × W ，SRM首先通过结合全局平均池和全局标准差池化的风格式池化收集全局信息。然后使用通道全连接层（即每个通道全连接）、批量归一化BN和sigmoid函数σ来提供注意力向量。最后，与SE块一样，输入特征乘以注意力向量。它利用输入特征的均值和标准差来提高捕获全局信息的能力。为了降低计算层（CFC）的完全连接要求，在全连接的地方也采用了CFC。通过将各个style的相对重要性纳入特征图，SRM有效地增强了CNN的表示能力。重点是轻量级，引入的参数非常少，同时效果还优于SENet.。

GCT

论文: GCT
代码: https://github.com/z-x-yang/GCT

GCT是由百度提出，一种通用且轻量型变化单元，结合了归一化和注意力机制，分析通道之间的相互关系（竞争or协作），对SENet中的squeeze、excitation和scale部分进行更新：在squeeze部分中使用L2 norm进行了global context embeding，同时在excitation中，仍然使用L2 norm 对通道归一化，在scale中通过设置权重γ和偏置β来控制通道特征是否激活。当一个通道的特征权重γc被正激活，GCT将促进这个通道的特征和其它通道的特征“竞争”。当一个通道的特征 γc 被负激活，GCT将促进这个通道的特征和其它通道的特征“合作”。

参考论文

• [1] Squeeze-and-Excitation Networks
• [2] Global Second-order Pooling Convolutional Networks
• [3] FcaNet: Frequency Channel Attention Networks
• [4] ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks
• [5] SRM : A Style-based Recalibration Module for Convolutional Neural Networks
• [6] Gated Channel Transformation for Visual Recognition
• [7] Recurrent Models of Visual Attention

具体链接见对应介绍！

总结：
本篇主要介绍注意力机制中的通道注意力机制，对通道注意力机制方法进行详细讲解，通道注意力机制在计算机视觉中，更关注特征图中channel之间的关系，重点对SENet、ECANe进行重点讲解，下篇将对空间注意力机制展开详细介绍.