回溯: 字符串的排列



回溯:78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

Solution1 回溯
https://leetcode.com/problems/subsets/comments/1011321
https://leetcode.com/problems/subsets/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-gao-/
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
if (startIndex >= nums.size()) { // 终止条件可以不加
return;
}
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
回溯: 39. 组合总和
Solution1 暴力
Solution2 回溯
class Solution {
public:
void dfs(vector<int>& candidates, int target, vector<vector<int>>& ans, vector<int>& combine, int idx) {
if (idx == candidates.size()) {
return;
}
if (target == 0) {
ans.emplace_back(combine);
return;
}
// 直接跳过
dfs(candidates, target, ans, combine, idx + 1);
// 选择当前数
if (target - candidates[idx] >= 0) {
combine.emplace_back(candidates[idx]);
dfs(candidates, target - candidates[idx], ans, combine, idx);
combine.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int>> ans;
vector<int> combine;
dfs(candidates, target, ans, combine, 0);
return ans;
}
};


回溯: 40. 组合总和 II
Solution1 回溯
方法一:回溯
思路与算法
由于我们需要求出所有和为 \textit{target}target 的组合,并且每个数只能使用一次,因此我们可以使用递归 + 回溯的方法来解决这个问题:
我们用 \textit{dfs}(\textit{pos}, \textit{rest})dfs(pos,rest) 表示递归的函数,其中 \textit{pos}pos 表示我们当前递归到了数组 \textit{candidates}candidates 中的第 \textit{pos}pos 个数,而 \textit{rest}rest 表示我们还需要选择和为 \textit{rest}rest 的数放入列表作为一个组合;
对于当前的第 \textit{pos}pos 个数,我们有两种方法:选或者不选。如果我们选了这个数,那么我们调用 \textit{dfs}(\textit{pos} + 1, \textit{rest} - \textit{candidates}[\textit{pos}])dfs(pos+1,rest−candidates[pos]) 进行递归,注意这里必须满足 \textit{rest} \geq \textit{candidates}[\textit{pos}]rest≥candidates[pos]。如果我们不选这个数,那么我们调用 \textit{dfs}(\textit{pos} + 1, \textit{rest})dfs(pos+1,rest) 进行递归;
在某次递归开始前,如果 \textit{rest}rest 的值为 00,说明我们找到了一个和为 \textit{target}target 的组合,将其放入答案中。每次调用递归函数前,如果我们选了那个数,就需要将其放入列表的末尾,该列表中存储了我们选的所有数。在回溯时,如果我们选了那个数,就要将其从列表的末尾删除。
上述算法就是一个标准的递归 + 回溯算法,但是它并不适用于本题。这是因为题目描述中规定了解集不能包含重复的组合,而上述的算法中并没有去除重复的组合。
例如当 \textit{candidates} = [2, 2]candidates=[2,2],\textit{target} = 2target=2 时,上述算法会将列表 [2][2] 放入答案两次。
因此,我们需要改进上述算法,在求出组合的过程中就进行去重的操作。我们可以考虑将相同的数放在一起进行处理,也就是说,如果数 \textit{x}x 出现了 yy 次,那么在递归时一次性地处理它们,即分别调用选择 0, 1, \cdots, y0,1,⋯,y 次 xx 的递归函数。这样我们就不会得到重复的组合。具体地:
我们使用一个哈希映射(HashMap)统计数组 \textit{candidates}candidates 中每个数出现的次数。在统计完成之后,我们将结果放入一个列表 \textit{freq}freq 中,方便后续的递归使用。
列表 \textit{freq}freq 的长度即为数组 \textit{candidates}candidates 中不同数的个数。其中的每一项对应着哈希映射中的一个键值对,即某个数以及它出现的次数。
在递归时,对于当前的第 \textit{pos}pos 个数,它的值为 \textit{freq}[\textit{pos}][0]freq[pos][0],出现的次数为 \textit{freq}[\textit{pos}][1]freq[pos][1],那么我们可以调用
\textit{dfs}(\textit{pos} + 1, \textit{rest} - i \times \textit{freq}[\textit{pos}][0])
dfs(pos+1,rest−i×freq[pos][0])
即我们选择了这个数 ii 次。这里 ii 不能大于这个数出现的次数,并且 i \times \textit{freq}[\textit{pos}][0]i×freq[pos][0] 也不能大于 \textit{rest}rest。同时,我们需要将 ii 个 \textit{freq}[\textit{pos}][0]freq[pos][0] 放入列表中。
这样一来,我们就可以不重复地枚举所有的组合了。
我们还可以进行什么优化(剪枝)呢?一种比较常用的优化方法是,我们将 \textit{freq}freq 根据数从小到大排序,这样我们在递归时会先选择小的数,再选择大的数。这样做的好处是,当我们递归到 \textit{dfs}(\textit{pos}, \textit{rest})dfs(pos,rest) 时,如果 \textit{freq}[\textit{pos}][0]freq[pos][0] 已经大于 \textit{rest}rest,那么后面还没有递归到的数也都大于 \textit{rest}rest,这就说明不可能再选择若干个和为 \textit{rest}rest 的数放入列表了。此时,我们就可以直接回溯。
class Solution {
private:
vector<pair<int, int>> freq;
vector<vector<int>> ans;
vector<int> sequence;
public:
void dfs(int pos, int rest) {
if (rest == 0) {
ans.push_back(sequence);
return;
}
if (pos == freq.size() || rest < freq[pos].first) {
return;
}
dfs(pos + 1, rest);
int most = min(rest / freq[pos].first, freq[pos].second);
for (int i = 1; i <= most; ++i) {
sequence.push_back(freq[pos].first);
dfs(pos + 1, rest - i * freq[pos].first);
}
for (int i = 1; i <= most; ++i) {
sequence.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
for (int num: candidates) {
if (freq.empty() || num != freq.back().first) {
freq.emplace_back(num, 1);
} else {
++freq.back().second;
}
}
dfs(0, target);
return ans;
}
};






回溯: 46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
Solution1 暴力
Solution2 回溯

class Solution {
public:
void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
// 所有数都填完了
if (first == len) {
res.emplace_back(output);
return;
}
for (int i = first; i < len; ++i) {
// 动态维护数组
swap(output[i], output[first]);
// 继续递归填下一个数
backtrack(res, output, first + 1, len);
// 撤销操作
swap(output[i], output[first]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
backtrack(res, nums, 0, (int)nums.size());
return res;
}
};
回溯:22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]
示例 2:
输入:n = 1
输出:[“()”]
提示:
1 <= n <= 8






Solution1 暴力

Solution2 递归 + 剪枝

回溯: 17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
示例 2:
输入:digits = “”
输出:[]
示例 3:
输入:digits = “2”
输出:[“a”,“b”,“c”]
提示:
0 <= digits.length <= 4
digits[i] 是范围 [‘2’, ‘9’] 的一个数字。
Solution 1 暴力
Simple and efficient iterative solution.
Explanation with sample input "123"
Initial state:
result = {""}
Stage 1 for number "1":
result has {""}
candiate is "abc"
generate three strings "" + "a", ""+"b", ""+"c" and put into tmp,
tmp = {"a", "b","c"}
swap result and tmp (swap does not take memory copy)
Now result has {"a", "b", "c"}
Stage 2 for number "2":
result has {"a", "b", "c"}
candidate is "def"
generate nine strings and put into tmp,
"a" + "d", "a"+"e", "a"+"f",
"b" + "d", "b"+"e", "b"+"f",
"c" + "d", "c"+"e", "c"+"f"
so tmp has {"ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf" }
swap result and tmp
Now result has {"ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf" }
Stage 3 for number "3":
result has {"ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf" }
candidate is "ghi"
generate 27 strings and put into tmp,
add "g" for each of "ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"
add "h" for each of "ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"
add "h" for each of "ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"
so, tmp has
{"adg", "aeg", "afg", "bdg", "beg", "bfg", "cdg", "ceg", "cfg"
"adh", "aeh", "afh", "bdh", "beh", "bfh", "cdh", "ceh", "cfh"
"adi", "aei", "afi", "bdi", "bei", "bfi", "cdi", "cei", "cfi" }
swap result and tmp
Now result has
{"adg", "aeg", "afg", "bdg", "beg", "bfg", "cdg", "ceg", "cfg"
"adh", "aeh", "afh", "bdh", "beh", "bfh", "cdh", "ceh", "cfh"
"adi", "aei", "afi", "bdi", "bei", "bfi", "cdi", "cei", "cfi" }
Finally, return result.
Soulution 2 回溯


Solution 3 队列



二分:0~n-1中缺失的数字


二分:162. 寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000
-231 <= nums[i] <= 231 - 1
对于所有有效的 i 都有 nums[i] != nums[i + 1]


Solution1 暴力

Solution2 二分法

int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right ) {
int mid = left + (right - left) / 2;
if (nums[mid] < nums[mid + 1]) {
left = mid+1;
} else {
right = mid+1;
}
}
return left;
}
二分: 旋转数组的最小数字


二分:33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104
Solution1 暴力
Solution2 二分查找


二分:34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109
Solution1 暴力
Solution2 二分


二分搜索讲解
https://www.bilibili.com/video/BV1fA4y1o715?spm_id_from=0.0.header_right.history_list.click
寻找target在数组里的左右边界,有如下三种情况:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int leftBorder = getLeftBorder(nums, target);
int rightBorder = getRightBorder(nums, target);
// 情况一
if (leftBorder == -2 || rightBorder == -2) return {-1, -1};
// 情况三
if (rightBorder - leftBorder > 1) return {leftBorder + 1, rightBorder - 1};
// 情况二
return {-1, -1};
}
private:
int getRightBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] > target) {
right = middle - 1;
} else { // 寻找右边界,nums[middle] == target的时候更新left
left = middle + 1;
rightBorder = left;
}
}
return rightBorder;
}
int getLeftBorder(vector<int>& nums, int target) {
int left = 0;
int right = nums.size() - 1;
int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
while (left <= right) {
int middle = left + ((right - left) / 2);
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新right
right = middle - 1;
leftBorder = right;
} else {
left = middle + 1;
}
}
return leftBorder;
}
};
二分: 35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
Solution1 暴力
public int searchInsert(int[] nums, int target) {
for(int i = 0; i < nums.length;i++){
if(nums[i] >= target){
return i;
}
}
return nums.length;
}
Solution2 二分
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int n = nums.size();
int left = 0;
int right = n; // 定义target在左闭右开的区间里,[left, right) target
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在 [middle+1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值的情况,直接返回下标
}
}
// 分别处理如下四种情况
// 目标值在数组所有元素之前 [0,0)
// 目标值等于数组中某一个元素 return middle
// 目标值插入数组中的位置 [left, right) ,return right 即可
// 目标值在数组所有元素之后的情况 [left, right),这是右开区间,return right 即可
return right;
}
};
二分:69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
Time Complexity: O(logn) | due to binary search using while loop.
Space Complexity: O(1) | as only 4 variables are initialized at the beginning. Which is constant irrespective of given input.
long long s=0, e=x, ans, mid; //long long due to some of test cases overflows integer limit.
while(s<=e){
mid=(s+e)/2;
if(mid*mid==x) return mid; //if the 'mid' value ever gives the result, we simply return it.
else if(mid*mid<x){
s=mid+1; //if 'mid' value encounterted gives lower result, we simply discard all the values lower than mid.
ans=mid; //an extra pointer 'ans' is maintained to keep track of only lowest 'mid' value.
}
else e=mid-1; //if 'mid' value encountered gives greater result, we simply discard all the values greater than mid.
}
return ans;
Solution1 暴力
Solution2 二分搜索

:287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
提示:
1 <= n <= 105
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗?
Overview
Finding the Duplicate Number is a classic problem, and as such there are many different ways to approach it; a total of 7 approaches are presented here. The first 4 approaches involve rearranging or modifying elements of the array, and hence do not meet the constraints specified in the problem statement. However, they are included here since they are more feasible to come up with as the first approach in an interview setting. Since each approach is independent of the other approaches, they can be read in any order.
Proof
Proving that at least one duplicate must exist in numsnums is an application of the pigeonhole principle. Here, each number in numsnums is a "pigeon" and each distinct number that can appear in numsnums is a "pigeonhole." Because there are n+1n+1 numbers and nn distinct possible numbers, the pigeonhole principle implies that if you were to put each of the n + 1n+1 pigeons into nn pigeonholes, at least one of the pigeonholes would have 2 or more pigeons.
Approach 1: Sort
Note: This approach modifies individual elements and does not use constant space, and hence does not meet the problem constraints. However, it utilizes a fundamental concept that can help solve similar problems.
Intuition
In an unsorted array, duplicate elements may be scattered across the array. However, in a sorted array, duplicate numbers will be next to each other.
Algorithm
Sort the input array (numsnums).
Iterate through the array, comparing the current number to the previous number (i.e. compare nums[i]nums[i] to nums[i - 1]nums[i−1] where i > 0i>0).
Return the first number that is equal to its predecessor.
Complexity Analysis
Time Complexity: O(n \log n)O(nlogn)
Sorting takes O(n \log n)O(nlogn) time. This is followed by a linear scan, resulting in a total of O(n \log n)O(nlogn) + O(n)O(n) = O(n \log n)O(nlogn) time.
Space Complexity: O(\log n)O(logn) or O(n)O(n)
The space complexity of the sorting algorithm depends on the implementation of each programming language:
In Java, Arrays.sort() for primitives is implemented using a variant of the Quick Sort algorithm, which has a space complexity of O(\log n)O(logn)
In C++, the sort() function provided by STL uses a hybrid of Quick Sort, Heap Sort and Insertion Sort, with a worst case space complexity of O(\log n)O(logn)
In Python, the sort() function is implemented using the Timsort algorithm, which has a worst-case space complexity of O(n)O(n)
Approach 2: Set
Note: This approach does not use constant space, and hence does not meet the problem constraints. However, it utilizes a fundamental concept that can help solve similar problems.
Intuition
As we traverse the array, we need a way to "remember" values that we've seen. If we come across a number that we've seen before, we've found the duplicate. An efficient way to record the seen values is by adding each number to a set as we iterate over the numsnums array.
Algorithm
In order to achieve linear time complexity, we need to be able to insert elements into a data structure and look them up in constant time. A HashSet/unordered_set is well suited for this purpose. Initialize an empty hashset, seenseen.
Iterate over the array and first check if the current element exists in the hashset (seenseen).
If it does exist in the hashset, that number is the duplicate and can be returned right away.
Otherwise, insert the current element into seenseen, move to the next element in the array and repeat step 2.
Complexity Analysis
Time Complexity: O(n)O(n)
HashSet insertions and lookups have amortized constant time complexities. Hence, this algorithm requires linear time, since it consists of a single for loop that iterates over each element, looking up the element and inserting it into the set at most once.
Space Complexity: O(n)O(n)
We use a set that may need to store at most nn elements, leading to a linear space complexity of O(n)O(n).
Solution1 二分法

class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size();
int l = 1, r = n - 1, ans = -1;
while (l <= r) {
int mid = (l + r) >> 1;
int cnt = 0;
for (int i = 0; i < n; ++i) {
cnt += nums[i] <= mid;
}
if (cnt <= mid) {
l = mid + 1;
} else {
r = mid - 1;
ans = mid;
}
}
return ans;
}
};
Solution2 二进制

class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size(), ans = 0;
// 确定二进制下最高位是多少
int bit_max = 31;
while (!((n - 1) >> bit_max)) {
bit_max -= 1;
}
for (int bit = 0; bit <= bit_max; ++bit) {
int x = 0, y = 0;
for (int i = 0; i < n; ++i) {
if (nums[i] & (1 << bit)) {
x += 1;
}
if (i >= 1 && (i & (1 << bit))) {
y += 1;
}
}
if (x > y) {
ans |= 1 << bit;
}
}
return ans;
}
};
Solution3 快慢指针


class Solution {
public:
int findDuplicate(vector<int>& nums) {
int slow = 0, fast = 0;
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
动态规划:53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
Solution1 暴力
Solution2 动态规划



Solution3 分治

动态规划:62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109
Since the robot can only move right and down, when it arrives at a point, it either arrives from left or above. If we use dp[i][j] for the number of unique paths to arrive at the point (i, j), then the state equation is dp[i][j] = dp[i][j - 1] + dp[i - 1][j]. Moreover, we have the base cases dp[0][j] = dp[i][0] = 1 for all valid i and j.
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 1));
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
The above solution runs in O(m * n) time and costs O(m * n) space. However, you may have noticed that each time when we update dp[i][j], we only need dp[i - 1][j] (at the previous row) and dp[i][j - 1] (at the current row). So we can reduce the memory usage to just two rows (O(n)).
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> pre(n, 1), cur(n, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
cur[j] = pre[j] + cur[j - 1];
}
swap(pre, cur);
}
return pre[n - 1];
}
};
Further inspecting the above code, pre[j] is just the cur[j] before the update. So we can further reduce the memory usage to one row.
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> cur(n, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
cur[j] += cur[j - 1];
}
}
return cur[n - 1];
}
};
Now, you may wonder whether we can further reduce the memory usage to just O(1) space since the above code seems to use only two variables (cur[j] and cur[j - 1]). However, since the whole row cur needs to be updated for m - 1 times (the outer loop) based on old values, all of its values need to be saved and thus O(1)-space is impossible. However, if you are having a DP problem without the outer loop and just the inner one, then it will be possible.
Solution1 排列组合

Solution2 动态规划
我们令 dp[i][j] 是到达 i, j 最多路径
动态方程:dp[i][j] = dp[i-1][j] + dp[i][j-1]
注意,对于第一行 dp[0][j],或者第一列 dp[i][0],由于都是在边界,所以只能为 1
时间复杂度:O(m*n)O(m∗n)
空间复杂度:O(m * n)O(m∗n)
优化:因为我们每次只需要 dp[i-1][j],dp[i][j-1]
所以我们只要记录这两个数,直接看代码吧!
思路二:
class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < n; i++) dp[0][i] = 1;
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}
优化1:空间复杂度 O(2n)O(2n)
class Solution {
public int uniquePaths(int m, int n) {
int[] pre = new int[n];
int[] cur = new int[n];
Arrays.fill(pre, 1);
Arrays.fill(cur,1);
for (int i = 1; i < m;i++){
for (int j = 1; j < n; j++){
cur[j] = cur[j-1] + pre[j];
}
pre = cur.clone();
}
return pre[n-1];
}
}
优化2:空间复杂度 O(n)O(n)
class Solution {
public int uniquePaths(int m, int n) {
int[] cur = new int[n];
Arrays.fill(cur,1);
for (int i = 1; i < m;i++){
for (int j = 1; j < n; j++){
cur[j] += cur[j-1] ;
}
}
return cur[n-1];
}
}
动态规划:64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例 1:
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
his is a typical DP problem. Suppose the minimum path sum of arriving at point (i, j) is S[i][j], then the state equation is S[i][j] = min(S[i - 1][j], S[i][j - 1]) + grid[i][j].
Well, some boundary conditions need to be handled. The boundary conditions happen on the topmost row (S[i - 1][j] does not exist) and the leftmost column (S[i][j - 1] does not exist). Suppose grid is like [1, 1, 1, 1], then the minimum sum to arrive at each point is simply an accumulation of previous points and the result is [1, 2, 3, 4].
Now we can write down the following (unoptimized) code.
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int> > sum(m, vector<int>(n, grid[0][0]));
for (int i = 1; i < m; i++)
sum[i][0] = sum[i - 1][0] + grid[i][0];
for (int j = 1; j < n; j++)
sum[0][j] = sum[0][j - 1] + grid[0][j];
for (int i = 1; i < m; i++)
for (int j = 1; j < n; j++)
sum[i][j] = min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j];
return sum[m - 1][n - 1];
}
};
As can be seen, each time when we update sum[i][j], we only need sum[i - 1][j] (at the current column) and sum[i][j - 1] (at the left column). So we need not maintain the full m*n matrix. Maintaining two columns is enough and now we have the following code.
Solution0 暴力
Solution1 动态规划

class Solution {
public int minPathSum(int[][] grid) {
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(i == 0 && j == 0) continue;
else if(i == 0) grid[i][j] = grid[i][j - 1] + grid[i][j];
else if(j == 0) grid[i][j] = grid[i - 1][j] + grid[i][j];
else grid[i][j] = Math.min(grid[i - 1][j], grid[i][j - 1]) + grid[i][j];
}
}
return grid[grid.length - 1][grid[0].length - 1];
}
}
动态规划:70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
提示:
1 <= n <= 45
The problem seems to be a dynamic programming one. Hint: the tag also suggests that!
Here are the steps to get the solution incrementally.
Base cases:
if n <= 0, then the number of ways should be zero.
if n == 1, then there is only way to climb the stair.
if n == 2, then there are two ways to climb the stairs. One solution is one step by another; the other one is two steps at one time.
The key intuition to solve the problem is that given a number of stairs n, if we know the number ways to get to the points [n-1] and [n-2] respectively, denoted as n1 and n2 , then the total ways to get to the point [n] is n1 + n2. Because from the [n-1] point, we can take one single step to reach [n]. And from the [n-2] point, we could take two steps to get there.
The solutions calculated by the above approach are complete and non-redundant. The two solution sets (n1 and n2) cover all the possible cases on how the final step is taken. And there would be NO overlapping among the final solutions constructed from these two solution sets, because they differ in the final step.
Now given the above intuition, one can construct an array where each node stores the solution for each number n. Or if we look at it closer, it is clear that this is basically a fibonacci number, with the starting numbers as 1 and 2, instead of 1 and 1.
Solution1 递归
class Solution {
public:
int climbStairs(int n) {
int dp0=1;
int dp1=1;
for(int i=2;i<=n;i++){
int tmp=dp0;
dp0=dp1;
dp1=tmp+dp1;
}
return dp1;
}
};
动态规划 91. 解码方法
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
‘A’ -> “1”
‘B’ -> “2”
…
‘Z’ -> “26”
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,“11106” 可以映射为:
“AAJF” ,将消息分组为 (1 1 10 6)
“KJF” ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 “06” 不能映射为 “F” ,这是由于 “6” 和 “06” 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
示例 1:
输入:s = “12”
输出:2
解释:它可以解码为 “AB”(1 2)或者 “L”(12)。
示例 2:
输入:s = “226”
输出:3
解释:它可以解码为 “BZ” (2 26), “VF” (22 6), 或者 “BBF” (2 2 6) 。
示例 3:
输入:s = “0”
输出:0
解释:没有字符映射到以 0 开头的数字。
含有 0 的有效映射是 ‘J’ -> “10” 和 ‘T’-> “20” 。
由于没有字符,因此没有有效的方法对此进行解码,因为所有数字都需要映射。
提示:
1 <= s.length <= 100
s 只包含数字,并且可能包含前导零。
通过次数235,094提交次数721,617


Solution1 动态规划

class Solution {
public:
int numDecodings(string s) {
if (s[0] == '0') return 0;
vector<int> dp(s.size()+1);
dp[0]=1;dp[1]=1;
for (int i =1; i < s.size(); i++) {
if (s[i] == '0')//1.s[i]为0的情况
if (s[i - 1] == '1' || s[i - 1] == '2') //s[i - 1]等于1或2的情况
dp[i+1] = dp[i-1];//由于s[1]指第二个下标,对应为dp[2],所以dp的下标要比s大1,故为dp[i+1]
else
return 0;
else //2.s[i]不为0的情况
if (s[i - 1] == '1' || (s[i - 1] == '2' && s[i] <= '6'))//s[i-1]s[i]两位数要小于26的情况
dp[i+1] = dp[i]+dp[i-1];
else//其他情况
dp[i+1] = dp[i];
}
return dp[s.size()];
}
};
Solution2 动态规划 空间复杂度优化为O(1)

树/动态规划: 96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19



Solution1 动态规划
结题思路:假设n个节点存在二叉排序树的个数是G(n),1为根节点,2为根节点,…,n为根节点,
当1为根节点时,其左子树节点个数为0,右子树节点个数为n-1,
同理当2为根节点时,其左子树节点个数为1,右子树节点为n-2,
所以可得G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)*G(0)
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
动态规划:121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104

I hope now question, approach is absolute clear.
code each line explained : Similar for C++, Java
{
int lsf = Integer.MAX_VALUE; // least so far
int op = 0; // overall profit
int pist = 0; // profit if sold today
for(int i = 0; i < prices.length; i++){
if(prices[i] < lsf){ // if we found new buy value which is more smaller then previous one
lsf = prices[i]; // update our least so far
}
pist = prices[i] - lsf; // calculating profit if sold today by, Buy - sell
if(op < pist){ // if pist is more then our previous overall profit
op = pist; // update overall profit
}
}
return op; // return op
Solution0 暴力解法
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = (int)prices.size(), ans = 0;
for (int i = 0; i < n; ++i){
for (int j = i + 1; j < n; ++j) {
ans = max(ans, prices[j] - prices[i]);
}
}
return ans;
}
};
Solution1 动态规划
动态规划 前i天的最大收益 = max{前i-1天的最大收益,第i天的价格-前i-1天中的最小价格}
class Solution {
public int maxProfit(int[] prices) {
if(prices.length <= 1)
return 0;
int min = prices[0], max = 0;
for(int i = 1; i < prices.length; i++) {
max = Math.max(max, prices[i] - min);
min = Math.min(min, prices[i]);
}
return max;
}
}
动态规划:122. 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104

Solution1 贪心算法

Solution2 动态规划

class Solution {
public int maxProfit(int[] prices) {
int [] dp = new int [prices.length+1];//这里从第0天开始,到底i天
dp[0] = 0;//第0天没有股票,最大利润为0
dp[1] = 0;//第一天只能买,不能买,因此最大利润也是0
for(int i = 1;i<prices.length;i++){
int A =dp[i]+prices[i]-prices[i-1];//第一种选择
int B = dp[i];//第二种选择
dp[i+1] = A>B ? A : B;//i从0开始,所以dp[I+1]是当前天数
}
return dp[prices.length];
动态规划:139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅有小写英文字母组成
wordDict 中的所有字符串 互不相同
We use a boolean vector dp[]. dp[i] is set to true if a valid word (word sequence) ends there. The optimization is to look from current position i back and only substring and do dictionary look up in case the preceding position j with dp[j] == true is found.
Solution1 动态规划
bool wordBreak(string s, vector<string>& wordDict) {
vector<bool> dp(s.size()+1, false);
unordered_set<string> m(wordDict.begin(), wordDict.end());
dp[0] = true;
for (int i = 1; i <= s.size(); ++i){
for (int j = 0; j < i; ++j){
if (dp[j] && m.find(s.substr(j, i-j)) != m.end()){
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
Solution2 动态规划 优化版
【优化】对于以上代码可以优化。每次并不需要从s[0]开始搜索。因为wordDict中的字符串长度是有限的。只需要从i-maxWordLength开始搜索就可以了
bool wordBreak(string s, vector<string>& wordDict) {
vector<bool> dp(s.size()+1, false);
unordered_set<string> m(wordDict.begin(), wordDict.end());
dp[0] = true;
//获取最长字符串长度
int maxWordLength = 0;
for (int i = 0; i < wordDict.size(); ++i){
maxWordLength = std::max(maxWordLength, (int)wordDict[i].size());
}
for (int i = 1; i <= s.size(); ++i){
for (int j = std::max(i-maxWordLength, 0); j < i; ++j){
if (dp[j] && m.find(s.substr(j, i-j)) != m.end()){
dp[i] = true;
break;
}
}
}
return dp[s.size()];
}
动态规划:152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104
-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
There can be Mutliple ways to frame the solution once we get the intuition right !! So, what should the intuition be ? Let's discuss that out !
Let's consider array to have no 0s (for the moment)......
So, on what factor does the answer depends now ?? It surely depends on the count of negative numbers in the array !!
There are 2 possibilities - either the count of -ve numbers is even or odd.... --->>>
If the count is even, then obviously we would want to include all of them(in fact the whole array) to maximise the product. As multiplying an even number of -ve numbers would make the result +ve.
If the count is odd, then we would want to exclude one -ve number from our product, so that the product gets maximised. So, now the question is, which -ve number to exclude? Example ---> arr={-2,-3,-1,-4,-5} which number should be excluded ? On observing it , we should get one fact clear, that the number which is going to get ignored is either going to be the first one or the last one.
Note that, we cannot exclude a -ve number that is not the first or the last, because, if we do so, we will need to exclude all(because you are breaking the product at this point) other -ve nums following that -ve number and then that needn't result in the maximum product.
Having said all that, now the question is whether to exclude the first -ve num or the last -ve num in the array. We can only know the answer by trying both.
So, firstly we will take the product from the beginning of the array and we will include the first -ve number and will leave out the last one !!
And will do the vice-versa for checking the other scenario !!
So , in that example we would leave the first -ve number... (-2 and then total_product will be product of rest of the numbers in array) or we would leave the last number...(-5) ... And maximum of those 2 cases will be the answer !!
Now, what if array has zeroes? Well, it changes nothing much to be honest, we can consider the part on both the side of 0 as the subarrays and the maximum product that way will be the max(subarray1_ans, subarray2_ans) .... And how to mark the division point ? How do we seperate the subarrays????...
Thats pretty simple and we have done it in kadane's algo, just make the curr_ongoing_prod=1 !! And maintain one maxm_prod variable seperately ....
Example -->>> arr={-2,1,4,5,0,-3,4,6,1,-2} .... so we can consider subarray1={-2,1,4,5} and subarray2={-3,4,6,-2} and then the max_ans(subarray1,subarray2) will be our answer !!
Let's have a look on our code now ....
Solution0 暴力
Solution1 动态规划

class Solution {
public:
int maxProduct(vector<int>& nums) {
int n = nums.size();
if(n == 0){
return 0;
} else if(n == 1) {
return nums[0];
}
int p = nums[0];
int maxP = nums[0];
int minP = nums[0];
for(int i = 1; i < n; i++) {
int t = maxP;
maxP = max(max(maxP * nums[i], nums[i]), minP *nums[i]);
minP = min(min(t * nums[i], nums[i]), minP * nums[i]);
p = max(maxP, p);
}
return p;
}
};
动态规划:198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 400
This is a classic 1D-DP problem where at every step we have a choice to make ...
So the first and foremost thing in any DP problem is to find the reccurence relation !!
At every ith house robber has 2 options: a) rob current house i. b) don't rob current house.
In case he is robbing the (i)th house, the money he can get till the i-th house == money robbed till (i-2)th house + money robbed at (i)th house....let's say total money robbed in this case equals to X.
In case he is not robbing, money robbed till i-th house==money robbed till (i-1)th house...lets say total money robbed in this case equals to Y.
So , the maxm money he gets till i-th house is the max(X,Y).
Example of case (a) --> nums={2,3,2} ... Here, the robber will rob the house at index-2 as nums[index-2] + nums[index-0] > nums[index-1]
Example of case (b)--> nums={2,7,3} ... here maximum money robbed till index-2 will not be equal to nums[index-2] + nums[index-0]... as nums[index-1] is greater than the sum of money at both those houses ...
We can achieve the desired solution to this problem via mutliple ways, let's start with the simpler ones and then will look forward to optimize the Time and Space Complexities
Simple Recursion
Time Complexcity : O ( 2^n ) Gives us TLE
Space Complexcity : O( 1 )
Solution1 动态规划
dp 方程 dp[i] = max(dp[i-2]+nums[i], dp[i-1])
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty()) {
return 0;
}
int size = nums.size();
if (size == 1) {
return nums[0];
}
vector<int> dp = vector<int>(size, 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < size; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[size - 1];
}
};
Solution2 动态规划
上述方法使用了数组存储结果。考虑到每间房屋的最高总金额只和该房屋的前两间房屋的最高总金额相关,因此可以使用滚动数组,在每个时刻只需要存储前两间房屋的最高总金额。
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.empty()) {
return 0;
}
int size = nums.size();
if (size == 1) {
return nums[0];
}
int first = nums[0], second = max(nums[0], nums[1]);
for (int i = 2; i < size; i++) {
int temp = second;
second = max(first + nums[i], second);
first = temp;
}
return second;
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是数组长度。只需要对数组遍历一次。
空间复杂度:O(1)O(1)。使用滚动数组,可以只存储前两间房屋的最高总金额,而不需要存储整个数组的结果,因此空间复杂度是 O(1)O(1)。
动态规划:221. 最大正方形

Approach 1: Brute Force
The simplest approach consists of trying to find out every possible square of 1’s that can be formed from within the matrix. The question now is – how to go for it?
We use a variable to contain the size of the largest square found so far and another variable to store the size of the current, both initialized to 0. Starting from the left uppermost point in the matrix, we search for a 1. No operation needs to be done for a 0. Whenever a 1 is found, we try to find out the largest square that can be formed including that 1. For this, we move diagonally (right and downwards), i.e. we increment the row index and column index temporarily and then check whether all the elements of that row and column are 1 or not. If all the elements happen to be 1, we move diagonally further as previously. If even one element turns out to be 0, we stop this diagonal movement and update the size of the largest square. Now we, continue the traversal of the matrix from the element next to the initial 1 found, till all the elements of the matrix have been traversed.
Complexity Analysis
Time complexity : O((mn)^2)
In worst case, we need to traverse the complete matrix for every 1.
Space complexity : O(1)O(1). No extra space is used.

Solution0 暴力法

Solution1 动态规划
class Solution {
public int maximalSquare(char[][] matrix) {
/**
dp[i][j]表示以第i行第j列为右下角所能构成的最大正方形边长, 则递推式为:
dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]);
**/
int m = matrix.length;
if(m < 1) return 0;
int n = matrix[0].length;
int max = 0;
int[][] dp = new int[m+1][n+1];
for(int i = 1; i <= m; ++i) {
for(int j = 1; j <= n; ++j) {
if(matrix[i-1][j-1] == '1') {
dp[i][j] = 1 + Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1]));
max = Math.max(max, dp[i][j]);
}
}
}
return max*max;
}
}
动态规划:279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
Idea:
This question is very similar to coin change https://leetcode.com/problems/coin-change/discuss/1104203/C%2B%2B-Super-Simple-and-Short-Dynamic-Programming-Solution.
The only difference is that in coin change we get a vector of coins and here we know that the coins are all the perfect squares.
So our first step will be to construct a "coin" vector.
Then, we do it the same way as coin change.
Solution1 动态规划

Solution2 数学

class Solution {
public:
// 判断是否为完全平方数
bool isPerfectSquare(int x) {
int y = sqrt(x);
return y * y == x;
}
// 判断是否能表示为 4^k*(8m+7)
bool checkAnswer4(int x) {
while (x % 4 == 0) {
x /= 4;
}
return x % 8 == 7;
}
int numSquares(int n) {
if (isPerfectSquare(n)) {
return 1;
}
if (checkAnswer4(n)) {
return 4;
}
for (int i = 1; i * i <= n; i++) {
int j = n - i * i;
if (isPerfectSquare(j)) {
return 2;
}
}
return 3;
}
};
动态规划:300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500
-104 <= nums[i] <= 104
进阶:
你能将算法的时间复杂度降低到 O(n log(n)) 吗?
✔️ Solution 1: Dynamic Programming
This is a classic Dynamic Programming problem.
Let dp[i] is the longest increase subsequence of nums[0..i] which has nums[i] as the end element of the subsequence.
Complexity
Time: O(N^2), where N <= 2500 is the number of elements in array nums.
Space: O(N)
✔️ Solution 2: Greedy with Binary Search
Let's construct the idea from following example.
Consider the example nums = [2, 6, 8, 3, 4, 5, 1], let's try to build the increasing subsequences starting with an empty one: sub1 = [].
Let pick the first element, sub1 = [2].
6 is greater than previous number, sub1 = [2, 6]
8 is greater than previous number, sub1 = [2, 6, 8]
3 is less than previous number, we can't extend the subsequence sub1, but we must keep 3 because in the future there may have the longest subsequence start with [2, 3], sub1 = [2, 6, 8], sub2 = [2, 3].
With 4, we can't extend sub1, but we can extend sub2, so sub1 = [2, 6, 8], sub2 = [2, 3, 4].
With 5, we can't extend sub1, but we can extend sub2, so sub1 = [2, 6, 8], sub2 = [2, 3, 4, 5].
With 1, we can't extend neighter sub1 nor sub2, but we need to keep 1, so sub1 = [2, 6, 8], sub2 = [2, 3, 4, 5], sub3 = [1].
Finally, length of longest increase subsequence = len(sub2) = 4.
In the above steps, we need to keep different sub arrays (sub1, sub2..., subk) which causes poor performance. But we notice that we can just keep one sub array, when new number x is not greater than the last element of the subsequence sub, we do binary search to find the smallest element >= x in sub, and replace with number x.
Let's run that example nums = [2, 6, 8, 3, 4, 5, 1] again:
Let pick the first element, sub = [2].
6 is greater than previous number, sub = [2, 6]
8 is greater than previous number, sub = [2, 6, 8]
3 is less than previous number, so we can't extend the subsequence sub. We need to find the smallest number >= 3 in sub, it's 6. Then we overwrite it, now sub = [2, 3, 8].
4 is less than previous number, so we can't extend the subsequence sub. We overwrite 8 by 4, so sub = [2, 3, 4].
5 is greater than previous number, sub = [2, 3, 4, 5].
1 is less than previous number, so we can't extend the subsequence sub. We overwrite 2 by 1, so sub = [1, 3, 4, 5].
Finally, length of longest increase subsequence = len(sub) = 4.
Complexity
Time: O(N * logN), where N <= 2500 is the number of elements in array nums.
Space: O(N), we can achieve O(1) in space by overwriting values of sub into original nums array.
Complexity:
Time: O(N * logN)
Space: O(N)
Solution1 动态规划

class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = (int)nums.size();
if (n == 0) {
return 0;
}
vector<int> dp(n, 0);
for (int i = 0; i < n; ++i) {
dp[i] = 1;
for (int j = 0; j < i; ++j) {
if (nums[j] < nums[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
return *max_element(dp.begin(), dp.end());
}
};

Solution2 贪心

class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int len = 1, n = (int)nums.size();
if (n == 0) {
return 0;
}
vector<int> d(n + 1, 0);
d[len] = nums[0];
for (int i = 1; i < n; ++i) {
if (nums[i] > d[len]) {
d[++len] = nums[i];
} else {
int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0
while (l <= r) {
int mid = (l + r) >> 1;
if (d[mid] < nums[i]) {
pos = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
d[pos + 1] = nums[i];
}
}
return len;
}
};
动态规划:313. 超级丑数
超级丑数 是一个正整数,并满足其所有质因数都出现在质数数组 primes 中。
给你一个整数 n 和一个整数数组 primes ,返回第 n 个 超级丑数 。
题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。
示例 1:
输入:n = 12, primes = [2,7,13,19]
输出:32
解释:给定长度为 4 的质数数组 primes = [2,7,13,19],前 12 个超级丑数序列为:[1,2,4,7,8,13,14,16,19,26,28,32] 。
示例 2:
输入:n = 1, primes = [2,3,5]
输出:1
解释:1 不含质因数,因此它的所有质因数都在质数数组 primes = [2,3,5] 中。
提示:
1 <= n <= 105
1 <= primes.length <= 100
2 <= primes[i] <= 1000
题目数据 保证 primes[i] 是一个质数
primes 中的所有值都 互不相同 ,且按 递增顺序 排列
It is actually like how we merge k sorted list:
ugly number k sorted list
1 2 7 13 19 1 * [2,7,13,19]
| | | | |
2 4 14 26 38 2 * [2,7,13,19]
| | | | |
4 8 28 52 76 4 * [2,7,13,19]
| | | | |
7 14 49 91 133 7 * [2,7,13,19]
| | | | |
8 16 56 ... ... 8 * [2,7,13,19]
| | | | |
. . . . .
. . . . .
. . . . .
We can see that each prime number in primes[] form a sorted list, and now our job is to merge them and find the nth minimum.
Here we don't have the next pointer for each node to trace the next potential candidate. But as we can see in the graph, we can make use of the ugly number we have produced so far!
Solution1 最小堆

class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
PriorityQueue<Long>queue=new PriorityQueue<>();
long res=1;
for(int i=1;i<n;i++){
for(int prime:primes){
queue.add(prime*res);
}
res=queue.poll();
while(!queue.isEmpty()&&res==queue.peek()) queue.poll();
}
return (int)res;
}
}
Solution2 动态规划

class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
vector<int> dp(n + 1); //用来存储丑数序列
dp[1] = 1; //第一个丑数是1
int m = primes.size();
vector<int> nums(m); //记录新丑数序列
vector<int> pointers(m, 1); //记录质数该与哪一位丑数做乘积
for (int i = 2; i <= n; i++) {
int minn = INT_MAX;
for (int j = 0; j < m; j++) {
nums[j] = dp[pointers[j]] * primes[j]; //旧丑数 * 质数序列 = 新丑数序列
minn = min(minn, nums[j]); //寻找所有新丑数中最小的丑数
}
dp[i] = minn;
for (int j = 0; j < m; j++)
if (minn == nums[j]) //如果此位置已经诞生过最小丑数
pointers[j]++; //让此位置所取旧丑数向后推一位
}
return dp[n];
}
};
动态规划/递归:322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104
If you carefully observe the below 3 codes. You will see that the DP Memoization is dervied from the Recursion code just by changing 3 lines and the DP Tabulation is derived from the DP Memoization.
Recursion
Time: O(2^n)
Space: O(n)
Writing a recursive function is all about find two things:
The base case: Just calculate the output for the smallest possible input
The choice diagram: For any given input, just see what all choices do we have.
DP Memoization
Time: O(n.m)
Space: O(n.m)
In the above recursive case, we were doing repeated work in the form of subproblems. Hence we store the results of those subproblems in a table to reduce the number of recursive calls.
DP Tabulation
Time: O(n.m)
Space: O(n.m)
We have reached the best conceivable run time for this question but since we have recursive calls in the previous algorithm. It might lead to stackoverflow error in the worst case when recursive calls are a lot. Hence we want to totally emit the notion of recursions. To do that, we simply convert the recursion into iterative code.
The below code is bottom up dynamic programming because we are starting from the first element in the 2D array and filling the DP from this first element till the last element. And eventually, the last cell stores our final result.
Solution1 动态规划

class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
int Max = amount + 1;
vector<int> dp(amount + 1, Max);
dp[0] = 0;
for (int i = 1; i <= amount; ++i) {
for (int j = 0; j < (int)coins.size(); ++j) {
if (coins[j] <= i) {
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
};
Solution2 贪心+回溯+剪枝


void coinChange(vector<int>& coins, int amount, int c_index, int count, int& ans) {
if (amount == 0) {
ans = min(ans, count);
return;
}
if (c_index == coins.size()) return;
for (int k = amount / coins[c_index]; k >= 0 && k + count < ans; k--) {
coinChange(coins, amount - k * coins[c_index], c_index + 1, count + k, ans);
}
}
int coinChange(vector<int>& coins, int amount) {
if (amount == 0) return 0;
sort(coins.rbegin(), coins.rend());
int ans = INT_MAX;
coinChange(coins, amount, 0, 0, ans);
return ans == INT_MAX ? -1 : ans;
}
树/动态规划: 337. 打家劫舍 III

Step I -- Think naively
At first glance, the problem exhibits the feature of "optimal substructure": if we want to rob maximum amount of money from current binary tree (rooted at root), we surely hope that we can do the same to its left and right subtrees.
So going along this line, let's define the function rob(root) which will return the maximum amount of money that we can rob for the binary tree rooted at root; the key now is to construct the solution to the original problem from solutions to its subproblems, i.e., how to get rob(root) from rob(root.left), rob(root.right), ... etc.
Apparently the analyses above suggest a recursive solution. And for recursion, it's always worthwhile figuring out the following two properties:
Termination condition: when do we know the answer to rob(root) without any calculation? Of course when the tree is empty ---- we've got nothing to rob so the amount of money is zero.
Recurrence relation: i.e., how to get rob(root) from rob(root.left), rob(root.right), ... etc. From the point of view of the tree root, there are only two scenarios at the end: root is robbed or is not. If it is, due to the constraint that "we cannot rob any two directly-linked houses", the next level of subtrees that are available would be the four "grandchild-subtrees" (root.left.left, root.left.right, root.right.left, root.right.right). However if root is not robbed, the next level of available subtrees would just be the two "child-subtrees" (root.left, root.right). We only need to choose the scenario which yields the larger amount of money.
However the solution runs very slowly (1186 ms) and barely got accepted (the time complexity turns out to be exponential, see my comments below).
Step II -- Think one step further
In step I, we only considered the aspect of "optimal substructure", but think little about the possibilities of overlapping of the subproblems. For example, to obtain rob(root), we need rob(root.left), rob(root.right), rob(root.left.left), rob(root.left.right), rob(root.right.left), rob(root.right.right); but to get rob(root.left), we also need rob(root.left.left), rob(root.left.right), similarly for rob(root.right). The naive solution above computed these subproblems repeatedly, which resulted in bad time performance. Now if you recall the two conditions for dynamic programming (DP): "optimal substructure" + "overlapping of subproblems", we actually have a DP problem. A naive way to implement DP here is to use a hash map to record the results for visited subtrees.
Step III -- Think one step back
In step I, we defined our problem as rob(root), which will yield the maximum amount of money that can be robbed of the binary tree rooted at root. This leads to the DP problem summarized in step II.
Now let's take one step back and ask why we have overlapping subproblems. If you trace all the way back to the beginning, you'll find the answer lies in the way how we have defined rob(root). As I mentioned, for each tree root, there are two scenarios: it is robbed or is not. rob(root) does not distinguish between these two cases, so "information is lost as the recursion goes deeper and deeper", which results in repeated subproblems.
If we were able to maintain the information about the two scenarios for each tree root, let's see how it plays out. Redefine rob(root) as a new function which will return an array of two elements, the first element of which denotes the maximum amount of money that can be robbed if root is not robbed, while the second element signifies the maximum amount of money robbed if it is robbed.
Let's relate rob(root) to rob(root.left) and rob(root.right)..., etc. For the 1st element of rob(root), we only need to sum up the larger elements of rob(root.left) and rob(root.right), respectively, since root is not robbed and we are free to rob its left and right subtrees. For the 2nd element of rob(root), however, we only need to add up the 1st elements of rob(root.left) and rob(root.right), respectively, plus the value robbed from root itself, since in this case it's guaranteed that we cannot rob the nodes of root.left and root.right.
As you can see, by keeping track of the information of both scenarios, we decoupled the subproblems and the solution essentially boiled down to a greedy one. Here is the program:
Solution1 动态规划

class Solution {
public:
unordered_map <TreeNode*, int> f, g;
void dfs(TreeNode* node) {
if (!node) {
return;
}
dfs(node->left);
dfs(node->right);
f[node] = node->val + g[node->left] + g[node->right];
g[node] = max(f[node->left], g[node->left]) + max(f[node->right], g[node->right]);
}
int rob(TreeNode* root) {
dfs(root);
return max(f[root], g[root]);
}
};
动态规划/背包:分割等和子集
背包问题 后面和回溯问题一起搞定
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
Solution
❌ Solution - I (Brute-Force)
Let's try solving it using brute-force approach. We need to partition the array into two subsets. This means that for each element of the array, we can either place it in 1st subset, or place it in 2nd subset.
Since we are only concerned with the sums of subset being equal, we will maintain 1st subset's sum: sum1 & 2nd subset's sum: sum2. For each element, we try both possible options of either placing it in 1st subset and increasing sum1 or placing it in 2nd subset & increasing sum2. Finally, once we reach the end of array, we can check if the current placements gave equal sum. If none of the possible placements give equal sum, we will return false.
We can slightly optimize the above approach by observing that equal partion are only possible when the total sum of array can be equally split, i.e, it is even. This effectively allows us to directly return false if the sum is odd. When the sum is even, we only need to check if we can construct one subset with its sum equal to total_sum / 2 (the other will automatically have the same sum, so we dont need to care about it). Thus the above can be optimized to -
Time Complexity : O(2N), where N is the number of elements in nums. For each element, we try both choices of including or excluding an element from subset leading to recursive branches 2*2*2..N times which give time complexity of O(2N)
Space Complexity : O(N), required by recursive stack
✔️ Solution - II (Dynamic Programming - Memoization)
The above solution times out because we were performing repeated calculations over and over unnecessarily. The result for a given parameters sum, i (can we achieve subset sum = sum starting from i index?) will always be the same. So once we have calculated it, we dont need to repea the whole calculation again when it is called from another recursive branch. Instead we can save the result for this state and return it whenever we called again.
Thus, we can use dynamic programming here. We use a dp array where dp[i][sum] denotes whether subset-sum = sum can be achieved or not starting from the ith index.
Initially all elements in dp are initialized to -1 denoting that we have not computed that state
If dp[i][sum] == 1 means that we can achieve sum starting from ith index
If dp[i][sum] == 0 means we cant achieve that sum starting from the ith index
Time Complexity : O(N*sum), where N is the number of elements in nums & sum is the sum of all elements in nums.
Space Complexity : O(N*sum), required by dp
✔️ Solution - III (Optimized Dynamic Programming - Memoization)
I am not sure if my reasoning is correct for this approach or it passes due to weak test cases. All other solutions I have seen are 2D memo. I initially thought this approach would fail but seems like it passes (tried on other OJs too).
We can further optimize the above memoization approach by reducing the state that we memoize. We used dp[i][sum] in the above approach to denote if sum can be achieved starting from ith element in nums. But we dont really care if we achieve the sum starting from i index or not. We are only concerned with whether we can achieve it or not. Thus, we can reduce the state down to 1D dp where dp[sum] denotes whether sum is possible to be achived from nums or not.
It is essential that we 1st recurse by choosing the current element and only then try the branch of not choosing. This prevents the recursive function from going all the way down the recursion tree by not choosing any elements and incorrectly marking sums as not achievable which could have been achievable if we had chosen earlier elements that we skipped.
I am not sure if this is best explanation but if someone can better explain or provide some kind of proof/reasoning as to why recursing by 1st picking the element & then not picking will guarantee correct answer, do comment below.
Time Complexity : O(N*sum)
Check the below image for illustration (Credits: @SanjayMarreddi)
Space Complexity : O(sum), required by dp
✔️ Solution - IV (Dynamic Programming - Tabulation)
We can convert the dp approach to iterative version. Here we will again use dp array, where dp[sum] will denote whether sum is achievable or not. Initially, we have dp[0] = true since a 0 sum is always achievable. Then for each element num, we will iterate & find if it is possible to form a sum j by adding num to some previously formable sum.
One thing to note that it is essential to iterate from right to left in the below inner loop to avoid marking multiple sum, say j1 as achievable and then again using that result to mark another bigger sum j2 (j2=j1+num) as achievable. This would be wrong since it would mean choosing num multiple times. So we start from right to left to avoid overwriting previous results updated in the current loop.
Time Complexity : O(N*sum)
Space Complexity : O(sum)
✔️ Solution - V (Dynamic Programming using bitmask)
We can use bitmasking to condense the inner loop of previous approach into a single bit-shift operation. Here we will use bitset in C++ consisting of sum number of bits (other language can use bigInt or whatever support is provided for such operations).
Each bit in bitset (dp[i]) will denote whether sum i is possible or not. Now, when we get a new number num, it can be added to every sum already possible, i.e, every dp[i] bit which is already 1. This operation can be performed using bit shift as dp << num. How? See the following example
Suppose current dp = 1011
This means sums 0, 1 and 3 are possible to achieve.
Let the next number we get: num = 5.
Now we can achieve (0, 1 & 3) which were already possible and (5, 6, 8) which are new sum after adding 'num=5' to previous sums
1. 'dp << num': This operation will add num to every bit .
3 2 1 0 8 7 6 5 4 3 2 1 0
So, dp = 1 0 1 1 will be transformed to dp = 1 0 1 1 0 0 0 0 0 (after 5 shifts to left)
Note that new dp now denotes 5, 6, 8 which are the new sums possible.
We will combine it with previous sums using '|' operation
8 7 6 5 4 3 2 1 0
2. 'dp | dp << num' = 1 0 1 1 0 1 0 1 1
And now we have every possible sum after combining new num with previous possible sums.
Finally, we will return dp[halfSum] denoting whether half sum is achievable or not.
Time Complexity : O(N*sum)
Space Complexity : O(sum)
动态规划:礼物的最大价值

动态规划: 连续子数组的最大和

动态规划:剪绳子







动态规划: 青蛙跳台阶




动态规划: 最长重复子数组
Approach #1: Brute Force with Initial Character Map [Time Limit Exceeded]
Intuition and Algorithm
In a typical brute force, for all starting indices i of A and j of B, we will check for the longest matching subarray A[i:i+k] == B[j:j+k] of length k. This would look roughly like the following psuedocode:
ans = 0
for i in [0 .. A.length - 1]:
for j in [0 .. B.length - 1]:
k = 0
while (A[i+k] == B[j+k]): k += 1 #and i+k < A.length etc.
ans = max(ans, k)
Our insight is that in typical cases, most of the time A[i] != B[j]. We could instead keep a hashmap Bstarts[A[i]] = all j such that B[j] == A[i], and only loop through those in our j loop.
Approach #2: Binary Search with Naive Check [Time Limit Exceeded]
Intuition
If there is a length k subarray common to A and B, then there is a length j <= k subarray as well.
Let check(length) be the answer to the question "Is there a subarray with length length, common to A and B?" This is a function with range that must take the form [True, True, ..., True, False, False, ..., False] with at least one True. We can binary search on this function.
Algorithm
Focusing on the binary search, our invariant is that check(hi) will always be False. We'll start with hi = min(len(A), len(B)) + 1; clearly check(hi) is False.
Now we perform our check in the midpoint mi of lo and hi. When it is possible, then lo = mi + 1, and when it isn't, hi = mi. This maintains the invariant. At the end of our binary search, hi == lo and lo is the lowest value such that check(lo) is False, so we want lo - 1.
As for the check itself, we can naively check whether any A[i:i+k] == B[j:j+k] using set structures.
Approach #3: Dynamic Programming [Accepted]
Intuition and Algorithm
Since a common subarray of A and B must start at some A[i] and B[j], let dp[i][j] be the longest common prefix of A[i:] and B[j:]. Whenever A[i] == B[j], we know dp[i][j] = dp[i+1][j+1] + 1. Also, the answer is max(dp[i][j]) over all i, j.
We can perform bottom-up dynamic programming to find the answer based on this recurrence. Our loop invariant is that the answer is already calculated correctly and stored in dp for any larger i, j.






动态规划:和为K的子数组
Brief note about Question-
We have to return the total number of continuous subarrays whose sum equals to k.
Let's take an example not given in the question by taking negative numbers
Suppose our arr is arr[]: [-1, -1, 1] && k = 0
So, the answer should be '1' as their is only one subarray whose sum is 0 i.e (-1 + 1)
Solution - I (Brute force, TLE)-
Since we are very obedient person and don't want to do anything extra from our side.
So, we will try to generate the sum of each subarray and if matches withk , then increment our answer.
Like, this is the most basic thing we can do.
Time Complexity --> O(n ^ 2) // where n is the size of the array
Space Complexity --> O(1) // we are not using anything extra from our side
It paases [ 85 / 89 ] in built test cases




动态规划:最长回文子串






位运算:268. 丢失的数字
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums = [3,0,1]
输出:2
解释:n = 3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 2:
输入:nums = [0,1]
输出:2
解释:n = 2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums 中。
示例 3:
输入:nums = [9,6,4,2,3,5,7,0,1]
输出:8
解释:n = 9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums 中。
示例 4:
输入:nums = [0]
输出:1
解释:n = 1,因为有 1 个数字,所以所有的数字都在范围 [0,1] 内。1 是丢失的数字,因为它没有出现在 nums 中。
提示:
n == nums.length
1 <= n <= 104
0 <= nums[i] <= n
nums 中的所有数字都 独一无二
The basic idea is to use XOR operation. We all know that a^b^b =a, which means two xor operations with the same number will eliminate the number and reveal the original number.
In this solution, I apply XOR operation to both the index and value of the array. In a complete array with no missing numbers, the index and value should be perfectly corresponding( nums[index] = index), so in a missing array, what left finally is the missing number.
Solution1 排序

Solution2 求和

Solution3 位运算

Solution4 哈希

位运算:338. 比特位计数\
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
提示:
0 <= n <= 105
进阶:
很容易就能实现时间复杂度为 O(n log n) 的解决方案,你可以在线性时间复杂度 O(n) 内用一趟扫描解决此问题吗?
你能不使用任何内置函数解决此问题吗?(如,C++ 中的 __builtin_popcount )

Solution1
方法一:i & (i - 1)可以去掉i最右边的一个1(如果有),因此 i & (i - 1)是比 i 小的,而且i & (i - 1)的1的个数已经在前面算过了,所以i的1的个数就是 i & (i - 1)的1的个数加上1
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 1;i<= num;i++){ //注意要从1开始,0不满足
res[i] = res[i & (i - 1)] + 1;
}
return res;
}
Solution2
方法二:i >> 1会把最低位去掉,因此i >> 1 也是比i小的,同样也是在前面的数组里算过。当 i 的最低位是0,则 i 中1的个数和i >> 1中1的个数相同;当i的最低位是1,i 中1的个数是 i >> 1中1的个数再加1
public int[] countBits(int num) {
int[] res = new int[num + 1];
for(int i = 0;i<= num;i++){
res[i] = res[i >> 1] + (i & 1); //注意i&1需要加括号
}
return res;
}
Solution3
分奇数和偶数:
偶数的二进制1个数超级简单,因为偶数是相当于被某个更小的数乘2,乘2怎么来的?在二进制运算中,就是左移一位,也就是在低位多加1个0,那样就说明dp[i] = dp[i / 2]
奇数稍微难想到一点,奇数由不大于该数的偶数+1得到,偶数+1在二进制位上会发生什么?会在低位多加1个1,那样就说明dp[i] = dp[i-1] + 1,当然也可以写成dp[i] = dp[i / 2] + 1
就这么简单!!!
class Solution {
public:
vector<int> countBits(int num) {
int i = 1;
vector<int> ans(num + 1);
for (int i = 0; i <= num; i++) {
if (i % 2 == 0)
ans[i] = ans[i / 2];
else
ans[i] = ans[i / 2] + 1;
}
return ans;
}
};
位运算:371. 两整数之和
给你两个整数 a 和 b ,不使用 运算符 + 和 - ,计算并返回两整数之和。
示例 1:
输入:a = 1, b = 2
输出:3
示例 2:
输入:a = 2, b = 3
输出:5
提示:
-1000 <= a, b <= 1000
Now we can not use the + operator, which means it is obvious that we have to use some sort of bit manupulation. But the real question is how?
The ans lies within the procedure of the addition, which I am going to show you below.
from binary level, how do we exactly add two numbers, let us see -->
_
a = 2 = 010
b = 3 = 011
------------
c = 5 = 101
In the position, where we have a dash above, there we are generating a carry, which will be carried over to the next bit, and added to that next bit. So, the addition pattern goes like -
0 0 1 1
+ 0 +1 + 0 + 1
---- ---- ---- ----
0 1 1 0 (with a carry 1)
Is this pattern similar to you? Have you seen this in the XOR table? Let's see the XOR table quickly -
a b | XOR
- - | - -
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 0
These are the exact same, hence for addition, we need to use the XOR operator. But what to do with the carry? Hey, we need to add that carry to the next bit, right? That is what we have seen in the implementation of the addition as well. We will do that only, but we can NOT use addition anyway.
But, before that, let's do the XOR for 2 and 3 example.
-- Doing only XOR --
a = 2 = 010
b = 3 = 011
------------
c = 1 = 001
1 is NOT our answer, and in this procedure, we have left the carry out, which is 100. Now what's the pattern for finding the carry? It is after we AND the two numbers, we will LEFT-SHIFT the result by 1. Didn't get it?
-- Doing only AND --
a = 2 = 010
b = 3 = 011
------------
c = 2 = 010
-----------
Doing Left-Shift by 1 (<<1)
-----------
c = 4 = 100
So, we found out the carry as well, and believe me or not, but it is the entire Algorithm. You have to repeat the steps of 1. XOR and 2. AND with Left-Shift, until the step no 2. becomes 0, and you will have your answer.
Example -
a = 2 = 010
b = 3 = 011
-----------
x = 1 = 001 = a
c = 4 = 100 = b
-----------
x = 5 = 101
c = 0 = 000
x = XOR & c = AND with Left-Shift
Since carry becomes 0, hence our answer is the XOR result = 5.
Below is the working code for the same, and you can run this code to find the desired answer.
class Solution {
public int getSum(int a, int b) {
while(b != 0){
int temp = (a&b)<<1;
a = a ^ b;
b = temp;
}
return a;
}
}
Time Complexity: O(1)
Space Complexity: O(1)
Time is O(1), because the max and min bounds are 1000 and -1000 respectively, which means the input will NOT be arbitrarily large, and it will be in the limits, hence the time will be constant.
The code for c and c++ will be very similar, and python will be a little different. If you like this approach, then please give me a thumbs up.
Thanks & Happy Coding :)
Solution1 位运算
int getSum(int a, int b)
{
int sum, carry;
sum = a ^ b; //异或这里可看做是相加但是不显现进位,比如5 ^ 3
/*0 1 0 1
0 0 1 1
------------
0 1 1 0
上面的如果看成传统的加法,不就是1+1=2,进1得0,但是这里没有显示进位出来,仅是相加,0+1或者是1+0都不用进位*/
carry = (a & b) << 1;
//相与为了让进位显现出来,比如5 & 3
/* 0 1 0 1
0 0 1 1
------------
0 0 0 1
上面的最低位1和1相与得1,而在二进制加法中,这里1+1也应该是要进位的,所以刚好吻合,但是这个进位1应该要再往前一位,所以左移一位*/
if(carry != 0) //经过上面这两步,如果进位不等于0,那么就是说还要把进位给加上去,所以用了尾递归,一直递归到进位是0。
{
return getSum(sum, carry);
}
return sum;
}
位运算:数组中数字出现的次数




位运算:不用加减乘除做加法

位运算:汉明距离
Solution I:
We use XOR bitwise operatoin to get all the bits that are set either in x or in y, not both.
Then we count the number of such bits and we're done!
class Solution {
public:
int hammingDistance(int x, int y) {
int res = 0;
int num = x^y;
while (num) {
res += num % 2;
num >>= 1;
}
return res;
}
};
Solution II - Without XOR:
We iterate x and y in parallel.
If (x % 2 != y % 2) - only one of the rightmost bits are set - we add one to res.
class Solution {
public:
int hammingDistance(int x, int y) {
int res = 0;
while (x || y) {
res += (x % 2 != y % 2);
x >>= 1, y >>= 1;
}
return res;
}
};


位运算:二进制中1的个数


位运算:数字的补数
✔️ Solution - I (Brute-Force)
We can simply iterate and find the leftmost bit (MSB) that is set. From that point onwards, we flip every bit till we reach the rightmost bit (LSB). To flip a bit, we can use ^ 1 (XOR 1) operation. This will flip a bit to 0 if it is set and flip to 1 if it is unset.
C++
class Solution {
public:
int findComplement(int num) {
int i = 31;
while((num & 1 << i) == 0) i--; // skip the left 0 bits till we reach the 1st set bit from left
while(i >= 0)
num ^= 1 << i--; // flip all bits by XORing with 1
return num;
}
};
Python
class Solution:
def findComplement(self, num):
i = 31
while (num & 1 << i) == 0:
i -= 1
while i >= 0:
num ^= 1 << i
i -= 1
return num
Time Complexity : O(N), where N is the number of bits. In this case, since we are starting from i=31, it should be constant but I am denoting time complexity of this approach as generalized O(N)
Space Complexity : O(1)
✔️ Solution - II (Bit-Manipulation Tricks)
The above method basically finds the leftmost set bit and XORs the remaining bits with 1. A more efficient way to do the same would be to simply XOR num with another number having all bits to the right of nums's 1st set bit as 1 and rest bit to left as 0. This would achieve the same thing as above.
For eg. num = 13
=> num = 13 (1101)
=> mask = 15 (1111)
--------------------
^ 2 (0010) We got all the bits flipped
But how to get mask?
A simple way would be to initialize mask = 0 and keep flipping bits of it to 1 starting from the rightmost bit (LSB) till we reach the leftmost set bit of num.
Now, how do we know that we reached the leftmost set bit in num?
We use another variable tmp = num. Each time, we will rightshift tmp essentially removing the rightmost bit. When we remove the leftmost set bit from it, it will become 0. Thus, we loop till tmp is not 0.
C++
class Solution {
public:
int findComplement(int num) {
int mask = 0; // all bits in mask are initially 0
for(int tmp = num; tmp; tmp >>= 1) // set bits in mask to 1 till we reach leftmost set bit in num
mask = (mask << 1) | 1; // leftshifts and sets the rightmost bit to 1
return mask ^ num; // finally XORing with mask will flip all bits in num
}
};
Python
class Solution:
def findComplement(self, num):
mask, tmp = 0, num
while tmp:
mask = (mask << 1) | 1
tmp >>= 1
return mask ^ num
Another way to do the same would be to the other way around and start with mask with all bits as 1. Then we keep setting rightmost bits in mask to 0 one by one till there are no common set bits left in num and mask (num & mask == 0 when no common set bits are present).
For eg. num = 13 (1101) and mask = -1 (111...1111) [all 32 set bits are set in -1 binary representation]
1. num = 000...1101
mask = 111...1110 => we still have common set bits
2. num = 000...1101
mask = 111...1100 => we still have common set bits
3. num = 000...1101
mask = 111...1000 => we still have common set bits
4. num = 000...1101
mask = 111...0000 => no more common bits left
Now what?
Now we can simply flip all bits in mask (using ~ operator). It will now have all rightmost bits set to one starting from leftmost set bit in num, i.e, we now have the same mask that we had in previous approach.
Now, we can XOR it with num and we get the flipped result
C++
class Solution {
public:
int findComplement(int num) {
uint mask = -1; // -1 is represented in binary as all bits set to 1
while(mask & num) mask <<= 1; // remove rightmost bits 1 by 1 till no common bits are left
return ~mask ^ num; // XORs with 1 & flips all bits in num starting from the leftmost set bit
}
};
Python
class Solution:
def findComplement(self, num):
mask = -1
while mask & num: mask <<= 1
return ~mask ^ num
This approach used 1 less operation inside loop (1st approach used 3 operations: right-shift >> on tmp, left-shift << on mask and | with 1 to set rightmost bit. This one uses 2: & to check if there are common bits in mask and num and left-shift << to remove the right set bits one by one)
Time Complexity : O(P) / O(log num), where P is the position of leftmost set bit in num. O(P) ~ O(log2(num))
Space Complexity : O(1)
✔️ Solution - III (Flip Bits from Right to Left)
We can start from the right-end and flip bits one by one. This is somewhat similar to 1st solution in above appraoch. But here we will not use mask but rather a bit starting with i=1 and just directly XOR it with num, then left-shift it & repeat thus flipping the bits in num one by one.
So, how do we know when to stop? We stop as soon i > num. This denotes that we have passed the leftmost set bit in num and thus we have flipped all the bits that needed to be flipped.
C++
class Solution {
public:
int findComplement(int num) {
int i = 1;
while(i <= num)
num ^= i,
i <<= 1;
return num;
}
};
Python
class Solution():
def findComplement(self, num):
i = 1
while i <= num:
num ^= i
i <<= 1
return num
Time Complexity : O(P) / O(log num)
Space Complexity : O(1)


递归: 24. 两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
Solution1 递归



Solution2 迭代


树/递归:95. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:
输入:n = 3
输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1
输出:[[1]]
提示:
1 <= n <= 8
The basic idea is that we can construct the result of n node tree just from the result of n-1 node tree.
Here's how we do it: only 2 conditions: 1) The nth node is the new root, so newroot->left = oldroot;
2) the nth node is not root, we traverse the old tree, every time the node in the old tree has a right child, we can perform: old node->right = nth node, nth node ->left = right child; and when we reach the end of the tree, don't forget we can also add the nth node here.
One thing to notice is that every time we push a TreeNode in our result, I push the clone version of the root, and I recover what I do to the old node immediately. This is because you may use the old tree for several times.
Solution1 回溯


树/递归:98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:true
示例 2:
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
树中节点数目范围在[1, 104] 内
-231 <= Node.val <= 231 - 1
For the recursive solution, we set a lower bound and a upper bound for the tree. When we recurse on the left subtree, the upper bound becomes the value of its root. When we recurse on the right subtree, the lower bound becomes the value of its root.
Solution1 递归
方法一: 递归
思路和算法
要解决这道题首先我们要了解二叉搜索树有什么性质可以给我们利用,由题目给出的信息我们可以知道:如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树。
这启示我们设计一个递归函数 helper(root, lower, upper) 来递归判断,函数表示考虑以 root 为根的子树,判断子树中所有节点的值是否都在 (l,r)(l,r) 的范围内(注意是开区间)。如果 root 节点的值 val 不在 (l,r)(l,r) 的范围内说明不满足条件直接返回,否则我们要继续递归调用检查它的左右子树是否满足,如果都满足才说明这是一棵二叉搜索树。
那么根据二叉搜索树的性质,在递归调用左子树时,我们需要把上界 upper 改为 root.val,即调用 helper(root.left, lower, root.val),因为左子树里所有节点的值均小于它的根节点的值。同理递归调用右子树时,我们需要把下界 lower 改为 root.val,即调用 helper(root.right, root.val, upper)。
函数递归调用的入口为 helper(root, -inf, +inf), inf 表示一个无穷大的值。
class Solution {
public:
bool helper(TreeNode* root, long long lower, long long upper) {
if (root == nullptr) {
return true;
}
if (root -> val <= lower || root -> val >= upper) {
return false;
}
return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MIN, LONG_MAX);
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次,因此时间复杂度为 O(n)O(n)。
空间复杂度:O(n)O(n),其中 nn 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,即二叉树的高度。最坏情况下二叉树为一条链,树的高度为 nn ,递归最深达到 nn 层,故最坏情况下空间复杂度为 O(n)O(n) 。
Solution2 中序遍历为升序
基于方法一中提及的性质,我们可以进一步知道二叉搜索树「中序遍历」得到的值构成的序列一定是升序的,这启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的,整棵树是二叉搜索树,否则不是,下面的代码我们使用栈来模拟中序遍历的过程。
可能有读者不知道中序遍历是什么,我们这里简单提及。中序遍历是二叉树的一种遍历方式,它先遍历左子树,再遍历根节点,最后遍历右子树。而我们二叉搜索树保证了左子树的节点的值均小于根节点的值,根节点的值均小于右子树的值,因此中序遍历以后得到的序列一定是升序序列。
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> stack;
long long inorder = (long long)INT_MIN - 1;
while (!stack.empty() || root != nullptr) {
while (root != nullptr) {
stack.push(root);
root = root -> left;
}
root = stack.top();
stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root -> val <= inorder) {
return false;
}
inorder = root -> val;
root = root -> right;
}
return true;
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 为二叉树的节点个数。二叉树的每个节点最多被访问一次,因此时间复杂度为 O(n)O(n)。
空间复杂度:O(n)O(n),其中 nn 为二叉树的节点个数。栈最多存储 nn 个节点,因此需要额外的 O(n)O(n) 的空间。
树/递归:101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:
输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
Explanation :
class Solution {
public:
bool solve(TreeNode * r1, TreeNode * r2)
{
// See the tree diagram are r1 and r2 null ? No, so this line dont execute
if(r1 == NULL && r2 == NULL)
return true;
// Is any one of r1 or r2 null ? Or are these values different ? No. Both values are
// same so this else if wont execute either
else if(r1 == NULL || r2 == NULL || r1->val != r2->val)
return false;
// Now comes the main part, we are calling 2 seperate function calls
return solve(r1->left, r2->right) && solve(r1->right, r2->left);
// First solve() before && will execute
// r1->left is 3 and r2->right = 3
// Both values are same , they will by pass both if and else if statement
// Now again r1->left is null and r2->right is null
// So they will return true from first if condtion
// Now the scene is : we have executed first solve() before && and it has
// returned us True so expression becomes ' return true && solve() '
// Now solve after && will execute
// Similarly it will check for 4 and 4 , it will by pass if else statements
// next time both will become null, so will return true
// Thus 2nd solve() at the end will also hold true
// and we know 'true && true' is true
// so true will be returned to caller, and thus tree is mirror of itself.
// Similarly you can check for any testcase, flow of execution will remain same.
}
bool isSymmetric(TreeNode* root)
{
// Imagine a tree: 1
// 2 2
// 3 4 4 3
// We are standing on root that is 1, function begins
// and now r1 and r2 points to 2 and 2 respectively.
return solve(root->left, root->right);
}
};
Solution1 递归

class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null) {
return true;
}
//调用递归函数,比较左节点,右节点
return dfs(root.left,root.right);
}
boolean dfs(TreeNode left, TreeNode right) {
//递归的终止条件是两个节点都为空
//或者两个节点中有一个为空
//或者两个节点的值不相等
if(left==null && right==null) {
return true;
}
if(left==null || right==null) {
return false;
}
if(left.val!=right.val) {
return false;
}
//再递归的比较 左节点的左孩子 和 右节点的右孩子
//以及比较 左节点的右孩子 和 右节点的左孩子
return dfs(left.left,right.right) && dfs(left.right,right.left);
}
}
Solution2 队列
回想下递归的实现:
当两个子树的根节点相等时,就比较:
左子树的 left 和 右子树的 right,这个比较是用递归实现的。
现在我们改用队列来实现,思路如下:
首先从队列中拿出两个节点(left 和 right)比较
将 left 的 left 节点和 right 的 right 节点放入队列
将 left 的 right 节点和 right 的 left 节点放入队列
时间复杂度是 O(n)O(n),空间复杂度是 O(n)O(n)
动画演示如下:
class Solution {
public boolean isSymmetric(TreeNode root) {
if(root==null || (root.left==null && root.right==null)) {
return true;
}
//用队列保存节点
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
//将根节点的左右孩子放到队列中
queue.add(root.left);
queue.add(root.right);
while(queue.size()>0) {
//从队列中取出两个节点,再比较这两个节点
TreeNode left = queue.removeFirst();
TreeNode right = queue.removeFirst();
//如果两个节点都为空就继续循环,两者有一个为空就返回false
if(left==null && right==null) {
continue;
}
if(left==null || right==null) {
return false;
}
if(left.val!=right.val) {
return false;
}
//将左节点的左孩子, 右节点的右孩子放入队列
queue.add(left.left);
queue.add(right.right);
//将左节点的右孩子,右节点的左孩子放入队列
queue.add(left.right);
queue.add(right.left);
}
return true;
}
}
递归:200. 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’

Solution1 DFS
思路:遍历岛这个二维数组,如果当前数为1,则进入感染函数并将岛个数+1
感染函数:其实就是一个递归标注的过程,它会将所有相连的1都标注成2。为什么要标注?这样就避免了遍历过程中的重复计数的情况,一个岛所有的1都变成了2后,遍历的时候就不会重复遍历了。建议没想明白的同学画个图看看。
class Solution {
public int numIslands(char[][] grid) {
int islandNum = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == '1'){
infect(grid, i, j);
islandNum++;
}
}
}
return islandNum;
}
//感染函数
public void infect(char[][] grid, int i, int j){
if(i < 0 || i >= grid.length ||
j < 0 || j >= grid[0].length || grid[i][j] != '1'){
return;
}
grid[i][j] = '2';
infect(grid, i + 1, j);
infect(grid, i - 1, j);
infect(grid, i, j + 1);
infect(grid, i, j - 1);
}
}
Solution2 BFS
主循环和思路一类似,不同点是在于搜索某岛屿边界的方法不同。
bfs 方法:
借用一个队列 queue,判断队列首部节点 (i, j) 是否未越界且为 1:
若是则置零(删除岛屿节点),并将此节点上下左右节点 (i+1,j),(i-1,j),(i,j+1),(i,j-1) 加入队列;
若不是则跳过此节点;
循环 pop 队列首节点,直到整个队列为空,此时已经遍历完此岛屿。
class Solution {
public int numIslands(char[][] grid) {
int count = 0;
for(int i = 0; i < grid.length; i++) {
for(int j = 0; j < grid[0].length; j++) {
if(grid[i][j] == '1'){
bfs(grid, i, j);
count++;
}
}
}
return count;
}
private void bfs(char[][] grid, int i, int j){
Queue<int[]> list = new LinkedList<>();
list.add(new int[] { i, j });
while(!list.isEmpty()){
int[] cur = list.remove();
i = cur[0]; j = cur[1];
if(0 <= i && i < grid.length && 0 <= j && j < grid[0].length && grid[i][j] == '1') {
grid[i][j] = '0';
list.add(new int[] { i + 1, j });
list.add(new int[] { i - 1, j });
list.add(new int[] { i, j + 1 });
list.add(new int[] { i, j - 1 });
}
}
}
}
递归:206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000
Well, since the head pointer may also be modified, we create a pre that points to it to facilitate the reverse process.
For the example list 1 -> 2 -> 3 -> 4 -> 5 in the problem statement, it will become 0 -> 1 -> 2 -> 3 -> 4 -> 5 (we init pre -> val to be 0). We also set a pointer cur to head. Then we keep inserting cur -> next after pre until cur becomes the last node. This idea uses three pointers (pre, cur and temp). You may implement it as follows.
Solution1 迭代
/迭代法
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while(cur!=null) {
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}
Solution2 递归
//尾递归
public ListNode reverseList(ListNode head) {
return reverse(null,head);
}
private static ListNode reverse(ListNode pre,ListNode cur){
if(cur==null) return pre;
ListNode next = cur.next;
cur.next = pre;
return reverse(cur,next);
}
树/递归:235. 二叉搜索树的最近公共祖先

Well, remember to take advantage of the property of binary search trees, which is, node -> left -> val < node -> val < node -> right -> val. Moreover, both p and q will be the descendants of the root of the subtree that contains both of them. And the root with the largest depth is just the lowest common ancestor. This idea can be turned into the following simple recursive code.
Solution1 非递归
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//如果根节点和p,q的差相乘是正数,说明这两个差值要么都是正数要么都是负数,也就是说
//他们肯定都位于根节点的同一侧,就继续往下找
while ((root.val - p.val) * (root.val - q.val) > 0)
root = p.val < root.val ? root.left : root.right;
//如果相乘的结果是负数,说明p和q位于根节点的两侧,如果等于0,说明至少有一个就是根节点
return root;
}
Solution2 递归
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//如果小于等于0,说明p和q位于root的两侧,直接返回即可
if ((root.val - p.val) * (root.val - q.val) <= 0)
return root;
//否则,p和q位于root的同一侧,就继续往下找
return lowestCommonAncestor(p.val < root.val ? root.left : root.right, p, q);
}
树/递归:236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
Approach 1: Recursive Approach
Intuition
The approach is pretty intuitive. Traverse the tree in a depth first manner. The moment you encounter either of the nodes p or q, return some boolean flag. The flag helps to determine if we found the required nodes in any of the paths. The least common ancestor would then be the node for which both the subtree recursions return a True flag. It can also be the node which itself is one of p or q and for which one of the subtree recursions returns a True flag.
Let us look at the formal algorithm based on this idea.
Algorithm
Start traversing the tree from the root node.
If the current node itself is one of p or q, we would mark a variable mid as True and continue the search for the other node in the left and right branches.
If either of the left or the right branch returns True, this means one of the two nodes was found below.
If at any point in the traversal, any two of the three flags left, right or mid become True, this means we have found the lowest common ancestor for the nodes p and q.
Complexity Analysis
Time Complexity: O(N)O(N), where NN is the number of nodes in the binary tree. In the worst case we might be visiting all the nodes of the binary tree.
Space Complexity: O(N)O(N). This is because the maximum amount of space utilized by the recursion stack would be NN since the height of a skewed binary tree could be NN.
Approach 2: Iterative using parent pointers
Intuition
If we have parent pointers for each node we can traverse back from p and q to get their ancestors. The first common node we get during this traversal would be the LCA node. We can save the parent pointers in a dictionary as we traverse the tree.
Algorithm
Start from the root node and traverse the tree.
Until we find p and q both, keep storing the parent pointers in a dictionary.
Once we have found both p and q, we get all the ancestors for p using the parent dictionary and add to a set called ancestors.
Similarly, we traverse through ancestors for node q. If the ancestor is present in the ancestors set for p, this means this is the first ancestor common between p and q (while traversing upwards) and hence this is the LCA node.
Complexity Analysis
Time Complexity : O(N)O(N), where NN is the number of nodes in the binary tree. In the worst case we might be visiting all the nodes of the binary tree.
Space Complexity : O(N)O(N). In the worst case space utilized by the stack, the parent pointer dictionary and the ancestor set, would be NN each, since the height of a skewed binary tree could be NN.
Solution1 递归
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return null;
// 如果p,q为根节点,则公共祖先为根节点
if (root.val == p.val || root.val == q.val) return root;
// 如果p,q在左子树,则公共祖先在左子树查找
if (find(root.left, p) && find(root.left, q)) {
return lowestCommonAncestor(root.left, p, q);
}
// 如果p,q在右子树,则公共祖先在右子树查找
if (find(root.right, p) && find(root.right, q)) {
return lowestCommonAncestor(root.right, p, q);
}
// 如果p,q分属两侧,则公共祖先为根节点
return root;
}
private boolean find(TreeNode root, TreeNode c) {
if (root == null) return false;
if (root.val == c.val) {
return true;
}
return find(root.left, c) || find(root.right, c);
}
}
递归:最小的K个数




树/递归:二叉搜索树与双向链表



树/递归: 二叉树的镜像




树/递归: 对称的二叉树

树/递归: 树的子结构


树/递归: 二叉树中和为某一个值的路径

递归/树:105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
Solution
You need to understand preorder and postorder traversal first, and then go ahead.
Basic idea is:
preorder[0] is the root node of the tree
preorder[x] is a root node of a sub tree
In in-order traversal
When inorder[index] is an item in the in-order traversal
inorder[0]-inorder[index-1] are on the left branch
inorder[index+1]-inorder[size()-1] are on the right branch
if there is nothing on the left, that means the left child of the node is NULL
if there is nothing on the right, that means the right child of the node is NULL
Algorithm:
Start from rootIdx 0
Find preorder[rootIdx] from inorder, let's call the index pivot
Create a new node with inorder[pivot]
Create its left child recursively
Create its right child recursively
Return the created node.
The implementation is self explanatory. Have a look :)
Solution1 递归
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
// preorder: [root, [left], [right]]
// inorder: [[left], root, [right]]
return buildTree(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
}
TreeNode* buildTree(vector<int>& preorder, int lo1, int hi1, vector<int>& inorder, int lo2, int hi2) {
if (lo1 > hi1 || lo2 > hi2) return nullptr;
int root = preorder[lo1];
int mid = lo2;
// 在 inorder 中查找 root 位置
for (int i = lo2; i <= hi2; ++i) {
if (inorder[i] == root) {
mid = i;
break;
}
}
auto s = new TreeNode(root);
// 下面的数组表示分割长度
// inorder: [mid-lo2, mid, hi2-mid]
// preorder:[root, mid-lo2, hi2-mid]
s->left = buildTree(preorder, lo1+1, lo1+mid-lo2, inorder, lo2, mid-1);
s->right = buildTree(preorder, lo1+mid-lo2+1, hi1, inorder, mid+1, hi2);
return s;
}
};
Solution2
class Solution {
public:
int getLength(ListNode* head) {
int ret = 0;
for (; head != nullptr; ++ret, head = head->next);
return ret;
}
TreeNode* buildTree(ListNode*& head, int left, int right) {
if (left > right) {
return nullptr;
}
int mid = (left + right + 1) / 2;
TreeNode* root = new TreeNode();
root->left = buildTree(head, left, mid - 1);
root->val = head->val;
head = head->next;
root->right = buildTree(head, mid + 1, right);
return root;
}
TreeNode* sortedListToBST(ListNode* head) {
int length = getLength(head);
return buildTree(head, 0, length - 1);
}
};
递归/树:109. 有序链表转换二叉搜索树
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。
示例 1:
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2:
输入: head = []
输出: []
提示:
head 中的节点数在[0, 2 * 104] 范围内
-105 <= Node.val <= 105
Recursively build tree.
find midpoint by fast/slow method, use middle node as root.
build left child by first half of the list
build right child by second half of the list (head is midpoint->next)
Solution1 先找中点 然后再左右分别构造
class Solution {
public TreeNode sortedListToBST(ListNode head) {
if(head == null) return null;
else if(head.next == null) return new TreeNode(head.val);
ListNode pre = head;
ListNode p = pre.next;
ListNode q = p.next;
//找到链表的中点p
while(q!=null && q.next!=null){
pre = pre.next;
p = pre.next;
q = q.next.next;
}
//将中点左边的链表分开
pre.next = null;
TreeNode root = new TreeNode(p.val);
root.left = sortedListToBST(head);
root.right = sortedListToBST(p.next);
return root;
}
}
递归/树:113. 路径总和 II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
树中节点总数在范围 [0, 5000] 内
-1000 <= Node.val <= 1000
-1000 <= targetSum <= 1000
Idea
DFS from the root down to it's descendants:
We need to keep current path (which stores elements in the path) so far.
We need to keep the remain targetSum so far (after minus value of elements in the path).
If we already reach into leaf node
Check if targetSum == 0 then we found a valid path from root to leaf node which sum equal to targetSum, so add current path to the answer.
Else dfs on left node and on the right node.
Complexity
Time: O(N^2), where N <= 5000 is the number of elements in the binary tree.
First, we think the time complexity is O(N) because we only visit each node once.
But we forgot to calculate the cost to copy the current path when we found a valid path, which in the worst case can cost O(N^2), let see the following example for more clear.
Extra Space (without counting output as space): O(H), where H is height of the binary tree. This is the space for stack recursion or keeping path so far.
Solution1 DFS
我们可以采用深度优先搜索的方式,枚举每一条从根节点到叶子节点的路径。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
复杂度分析

class Solution {
public:
vector<vector<int>> ret;
vector<int> path;
void dfs(TreeNode* root, int targetSum) {
if (root == nullptr) {
return;
}
path.emplace_back(root->val);
targetSum -= root->val;
if (root->left == nullptr && root->right == nullptr && targetSum == 0) {
ret.emplace_back(path);
}
dfs(root->left, targetSum);
dfs(root->right, targetSum);
path.pop_back();
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
dfs(root, targetSum);
return ret;
}
};
Solution2 BFS
方法二:广度优先搜索
思路及算法
我们也可以采用广度优先搜索的方式,遍历这棵树。当我们遍历到叶子节点,且此时路径和恰为目标和时,我们就找到了一条满足条件的路径。
为了节省空间,我们使用哈希表记录树中的每一个节点的父节点。每次找到一个满足条件的节点,我们就从该节点出发不断向父节点迭代,即可还原出从根节点到当前节点的路径。
class Solution {
public:
vector<vector<int>> ret;
unordered_map<TreeNode*, TreeNode*> parent;
void getPath(TreeNode* node) {
vector<int> tmp;
while (node != nullptr) {
tmp.emplace_back(node->val);
node = parent[node];
}
reverse(tmp.begin(), tmp.end());
ret.emplace_back(tmp);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return ret;
}
queue<TreeNode*> que_node;
queue<int> que_sum;
que_node.emplace(root);
que_sum.emplace(0);
while (!que_node.empty()) {
TreeNode* node = que_node.front();
que_node.pop();
int rec = que_sum.front() + node->val;
que_sum.pop();
if (node->left == nullptr && node->right == nullptr) {
if (rec == targetSum) {
getPath(node);
}
} else {
if (node->left != nullptr) {
parent[node->left] = node;
que_node.emplace(node->left);
que_sum.emplace(rec);
}
if (node->right != nullptr) {
parent[node->right] = node;
que_node.emplace(node->right);
que_sum.emplace(rec);
}
}
}
return ret;
}
};
从上到下打印二叉树|||


树/分治: 重建二叉树


树:最大二叉树
Approach 1: Recursive Solution
The current solution is very simple. We make use of a function construct(nums, l, r), which returns the maximum binary tree consisting of numbers within the indices ll and rr in the given numsnums array(excluding the r^{th}r
th
element).
The algorithm consists of the following steps:
Start with the function call construct(nums, 0, n). Here, nn refers to the number of elements in the given numsnums array.
Find the index, max_imax
i
, of the largest element in the current range of indices (l:r-1)(l:r−1). Make this largest element, nums[max\_i]nums[max_i] as the local root node.
Determine the left child using construct(nums, l, max_i). Doing this recursively finds the largest element in the subarray left to the current largest element.
Similarly, determine the right child using construct(nums, max_i + 1, r).
Return the root node to the calling function.

树: 把二叉搜索树转换成为累加树

树:二叉树的直径
'''
class Solution {
public:
int dia=0;
int diameterOfBinaryTree(TreeNode* root) {
//base case 1:
if(!root)
return 0;
//recursively, call the helper function with the root
helper(root);
//return the diameter value
return dia;
}
int helper(TreeNode* node){
//base case 2
if(!node)
return 0;
//initialize two pointers, left & right ones
int leftNode=helper(node->left);
int rightNode=helper(node->right);
//updated diameter value is the max path between two nodes-> path between two leaves
dia=max(dia, leftNode+rightNode);
//for each node-> add the diameter by one, as you pass an edge
return 1+max(leftNode, rightNode);
}
};


树:94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
Solution1 递归

Solution2 迭代
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> stk;
while (root != nullptr || !stk.empty()) {
while (root != nullptr) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
res.push_back(root->val);
root = root->right;
}
return res;
}
};
树:102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-1000 <= Node.val <= 1000
What is level in our binary tree? It is set of nodes, for which distance between root and these nodes are constant. And if we talk about distances, it can be a good idea to use bfs.
We put our root into queue, now we have level 0 in our queue.
On each step extract all nodes from queue and put their children to to opposite end of queue. In this way we will have full level in the end of each step and our queue will be filled with nodes from the next level.
In the end we just return result.
Complexity
Time complexity is O(n): we perform one bfs on our tree. Space complexity is also O(n), because we have answer of this size.
Code
Solution1 队列实现


class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector <vector <int>> ret;
if (!root) {
return ret;
}
queue <TreeNode*> q;
q.push(root);
while (!q.empty()) {
int currentLevelSize = q.size();
ret.push_back(vector <int> ());
for (int i = 1; i <= currentLevelSize; ++i) {
auto node = q.front(); q.pop();
ret.back().push_back(node->val);
if (node->left) q.push(node->left);
if (node->right) q.push(node->right);
}
}
return ret;
}
};
Solution2 递归实现
层序遍历一般来说确实是用队列实现的,但是这里很明显用递归前序遍历就能实现呀,而且复杂度O(n)。。。
要点有几个:
利用depth变量记录当前在第几层(从0开始),进入下层时depth + 1;
如果depth >= vector.size()说明这一层还没来过,这是第一次来,所以得扩容咯;
因为是前序遍历,中-左-右,对于每一层来说,左边的肯定比右边先被遍历到,实际上后序中序都是一样的。。。
代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
pre(root, 0, ans);
return ans;
}
void pre(TreeNode *root, int depth, vector<vector<int>> &ans) {
if (!root) return ;
if (depth >= ans.size())
ans.push_back(vector<int> {});
ans[depth].push_back(root->val);
pre(root->left, depth + 1, ans);
pre(root->right, depth + 1, ans);
}
};
树:103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100
Assuming after traversing the 1st level, nodes in queue are {9, 20, 8}, And we are going to traverse 2nd level, which is even line and should print value from right to left [8, 20, 9].
We know there are 3 nodes in current queue, so the vector for this level in final result should be of size 3.
Then, queue [i] -> goes to -> vector[queue.size() - 1 - i]
i.e. the ith node in current queue should be placed in (queue.size() - 1 - i) position in vector for that line.
For example, for node(9), it's index in queue is 0, so its index in vector should be (3-1-0) = 2.
Solution1 层序遍历
层序遍历,然后在奇数时逆序一下
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int> > res;
if(!root) return res;
queue<TreeNode *> q;
q.push(root);
int flag = 0;
while(!q.empty())
{
vector<int> out;
int size = q.size(); //取得每一层的长度
for(int i = 0; i < size; i++)
{
auto temp = q.front();
q.pop();
out.push_back(temp->val);
if(temp->left)
{
q.push(temp->left);
}
if(temp->right)
{
q.push(temp->right);
}
}
if(flag%2==1)
{
reverse(out.begin(),out.end());
}
res.push_back(out);
flag++;
}
return res;
}
};
树:104. 二叉树的最大深度


Solution1 DFS


Slution2 BFS

树:105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
olution
You need to understand preorder and postorder traversal first, and then go ahead.
Basic idea is:
preorder[0] is the root node of the tree
preorder[x] is a root node of a sub tree
In in-order traversal
When inorder[index] is an item in the in-order traversal
inorder[0]-inorder[index-1] are on the left branch
inorder[index+1]-inorder[size()-1] are on the right branch
if there is nothing on the left, that means the left child of the node is NULL
if there is nothing on the right, that means the right child of the node is NULL
Algorithm:
Start from rootIdx 0
Find preorder[rootIdx] from inorder, let's call the index pivot
Create a new node with inorder[pivot]
Create its left child recursively
Create its right child recursively
Return the created node.
The implementation is self explanatory. Have a look :)
树:144. 二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
输入:root = [1,null,2,3]
输出:[1,2,3]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
示例 4:
输入:root = [1,2]
输出:[1,2]
示例 5:
输入:root = [1,null,2]
输出:[1,2]
提示:
树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
There are three solutions to this problem.
Iterative solution using stack --- O(n) time and O(n) space;
Recursive solution --- O(n) time and O(n) space (function call stack);
Morris traversal --- O(n) time and O(1) space.
Solution1 递归

Solution2 迭代

class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> res;
if (root == nullptr) {
return res;
}
stack<TreeNode*> stk;
TreeNode* node = root;
while (!stk.empty() || node != nullptr) {
while (node != nullptr) {
res.emplace_back(node->val);
stk.emplace(node);
node = node->left;
}
node = stk.top();
stk.pop();
node = node->right;
}
return res;
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。
空间复杂度:O(n)O(n),为迭代过程中显式栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。
树:199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:
输入: [1,null,3]
输出: [1,3]
示例 3:
输入: []
输出: []
提示:
二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

Solution1 层序遍历
使用层序遍历,并只保留每层最后一个节点的值
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
unordered_map<int, int> rightmostValueAtDepth;
int max_depth = -1;
queue<TreeNode*> nodeQueue;
queue<int> depthQueue;
nodeQueue.push(root);
depthQueue.push(0);
while (!nodeQueue.empty()) {
TreeNode* node = nodeQueue.front();nodeQueue.pop();
int depth = depthQueue.front();depthQueue.pop();
if (node != NULL) {
// 维护二叉树的最大深度
max_depth = max(max_depth, depth);
// 由于每一层最后一个访问到的节点才是我们要的答案,因此不断更新对应深度的信息即可
rightmostValueAtDepth[depth] = node -> val;
nodeQueue.push(node -> left);
nodeQueue.push(node -> right);
depthQueue.push(depth + 1);
depthQueue.push(depth + 1);
}
}
vector<int> rightView;
for (int depth = 0; depth <= max_depth; ++depth) {
rightView.push_back(rightmostValueAtDepth[depth]);
}
return rightView;
}
};

这里可以通过维护两个node queue来实现
树:226. 翻转二叉树

To invert a binary tree, we swap the left and right subtrees and invert them recursively/iteratively.
Solution1
利用前序遍历
class Solution {
// 先序遍历--从顶向下交换
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;
// 保存右子树
TreeNode rightTree = root.right;
// 交换左右子树的位置
root.right = invertTree(root.left);
root.left = invertTree(rightTree);
return root;
}
}
利用中序遍历
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) return null;
invertTree(root.left); // 递归找到左节点
TreeNode rightNode= root.right; // 保存右节点
root.right = root.left;
root.left = rightNode;
// 递归找到右节点 继续交换 : 因为此时左右节点已经交换了,所以此时的右节点为root.left
invertTree(root.left);
}
}
利用后序遍历
class Solution {
public TreeNode invertTree(TreeNode root) {
// 后序遍历-- 从下向上交换
if (root == null) return null;
TreeNode leftNode = invertTree(root.left);
TreeNode rightNode = invertTree(root.right);
root.right = leftNode;
root.left = rightNode;
return root;
}
}
利用层次遍历
class Solution {
public TreeNode invertTree(TreeNode root) {
// 层次遍历--直接左右交换即可
if (root == null) return null;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode node = queue.poll();
TreeNode rightTree = node.right;
node.right = node.left;
node.left = rightTree;
if (node.left != null){
queue.offer(node.left);
}
if (node.right != null){
queue.offer(node.right);
}
}
return root;
}
}
230. 二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。

Solution1 非递归
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode*> s;
int num=0;
TreeNode *cur=root;
while(!s.empty() || cur)
{
if(cur)
{
s.push(cur);
cur=cur->left;
}
else
{
cur=s.top();
s.pop();
num++;
if(num==k)
return cur->val;
cur=cur->right;
}
}
return 0;
}
};
Solution2 记录子节点数目

class MyBst {
public:
MyBst(TreeNode *root) {
this->root = root;
countNodeNum(root);
}
// 返回二叉搜索树中第k小的元素
int kthSmallest(int k) {
TreeNode *node = root;
while (node != nullptr) {
int left = getNodeNum(node->left);
if (left < k - 1) {
node = node->right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node->left;
}
}
return node->val;
}
private:
TreeNode *root;
unordered_map<TreeNode *, int> nodeNum;
// 统计以node为根结点的子树的结点数
int countNodeNum(TreeNode * node) {
if (node == nullptr) {
return 0;
}
nodeNum[node] = 1 + countNodeNum(node->left) + countNodeNum(node->right);
return nodeNum[node];
}
// 获取以node为根结点的子树的结点数
int getNodeNum(TreeNode * node) {
if (node != nullptr && nodeNum.count(node)) {
return nodeNum[node];
}else{
return 0;
}
}
};
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
MyBst bst(root);
return bst.kthSmallest(k);
}
};
二叉搜索树的第K大节点

树:114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

Solution1 递归
TreeNode* last = nullptr;
void flatten(TreeNode* root) {
if (root == nullptr) return;
flatten(root->right);
flatten(root->left);
root->right = last;
root->left = nullptr;
last = root;
}
Solution2 迭代
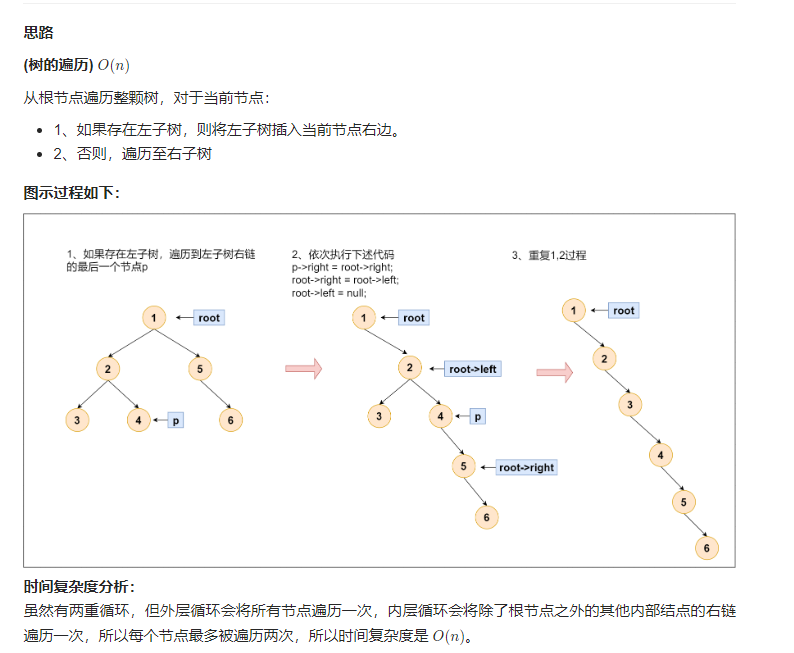
class Solution {
public:
void flatten(TreeNode* root) {
while(root){
TreeNode* p = root->left;
if(p){
while(p->right) p = p->right;
p->right = root->right;
root->right = root->left;
root->left = nullptr;
}
root = root->right;
}
}
};