1. Two Sum
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
Solution 1
双层遍历
Solution 2
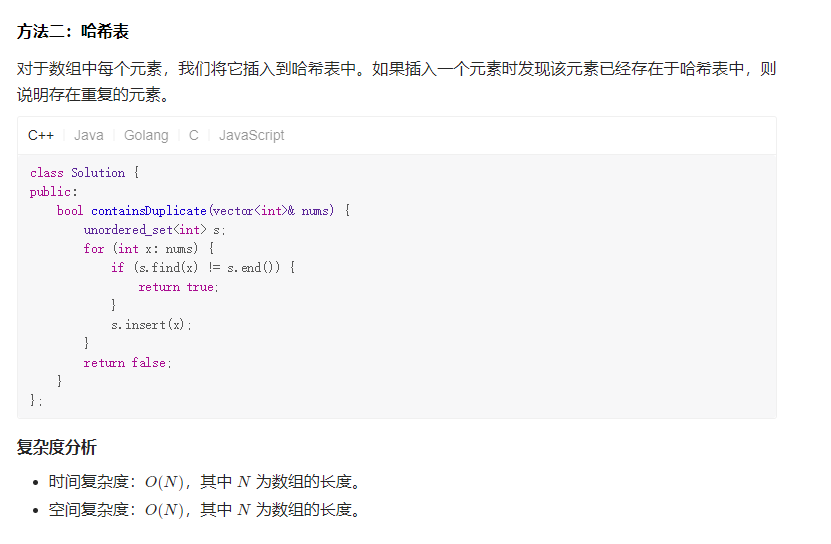
哈希表
The basic idea is to maintain a hash table for each element num in nums,
using num as key and its index (0-based) as value. For each num,
search for target - num in the hash table.
If it is found and is not the same element as num, then we are done.
The code is as follows. Note that each time before we add num to mp,
we search for target - num first and so we will not hit the same element.
18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例 2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]
提示:
1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109
Solution 1 暴力枚举
Solution 2 双指针法
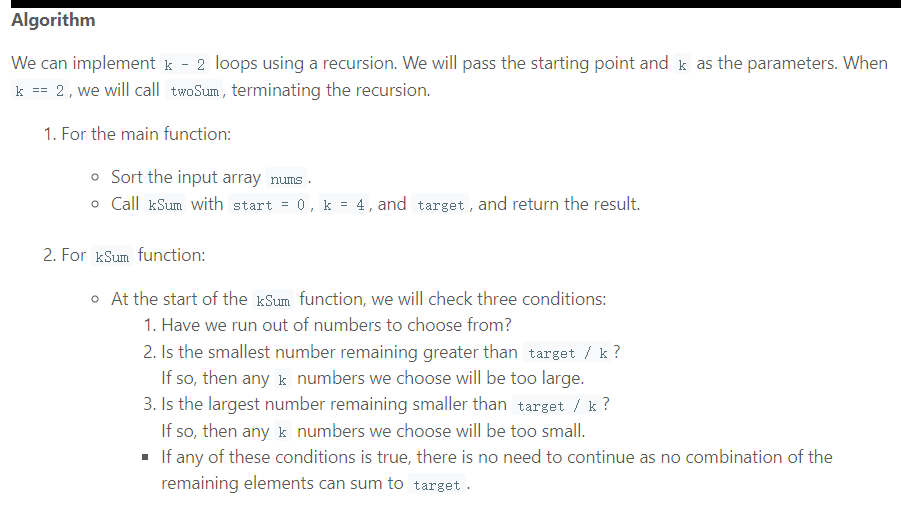
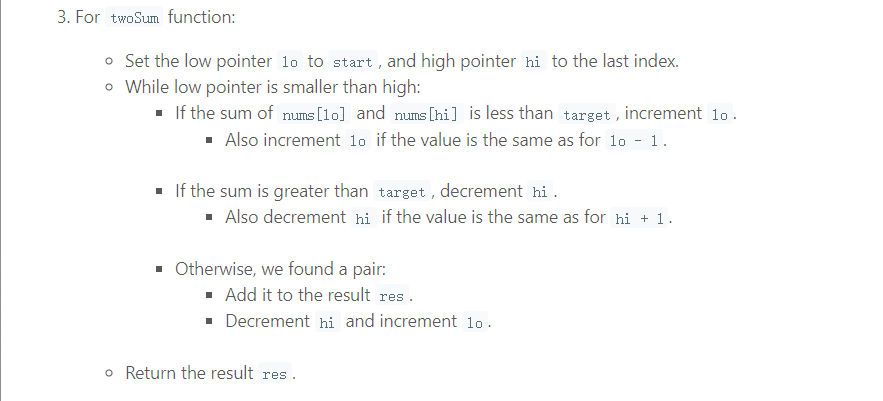
The two pointers pattern requires the array to be sorted, so we do that first. Also, it's easier to deal with duplicates if the array is sorted: repeated values are next to each other and easy to skip.
For 3Sum, we enumerate each value in a single loop, and use the two pointers pattern for the rest of the array. For kSum, we will have k - 2 nested loops to enumerate all combinations of k - 2 values.


19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2:
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
提示:
链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz
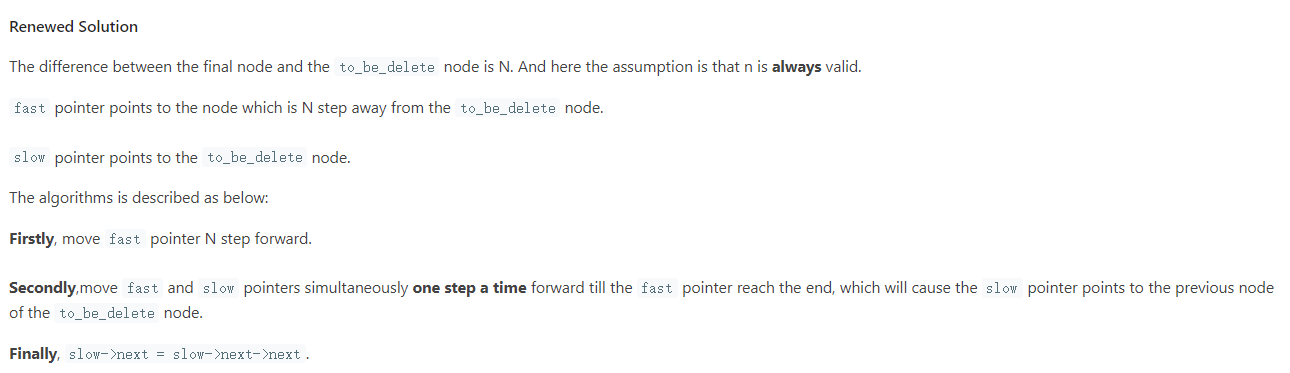
Solution1 计算链表长度
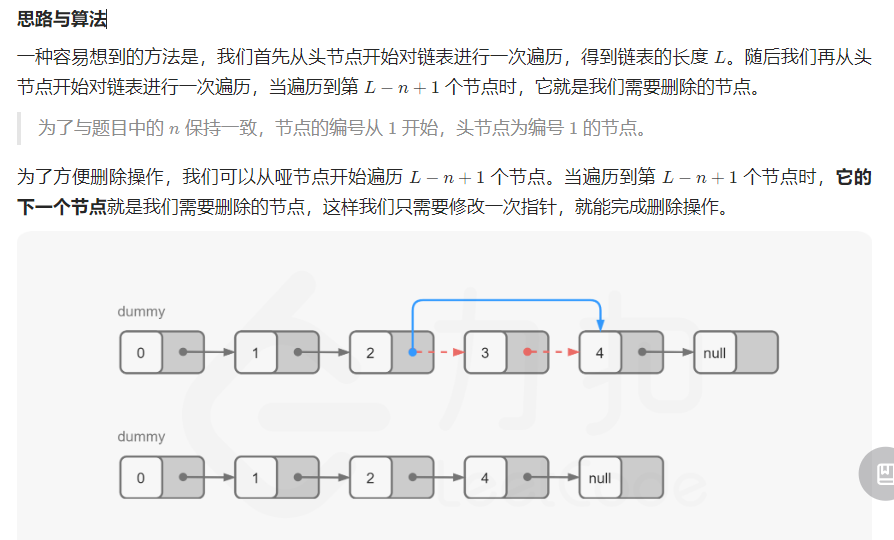
Solution2 栈

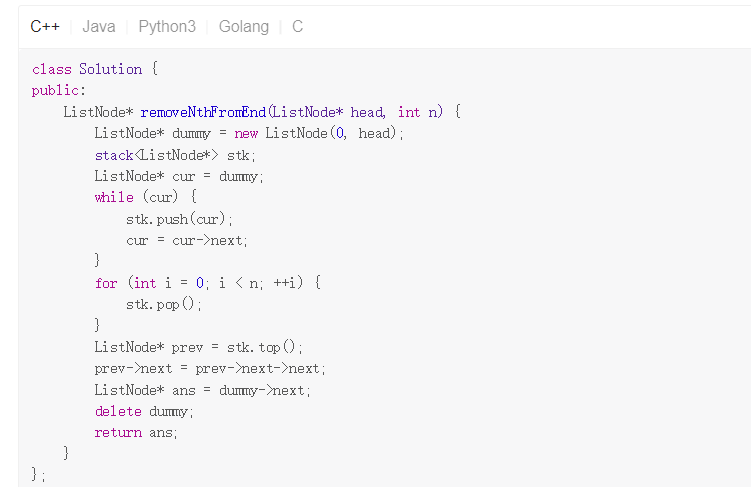
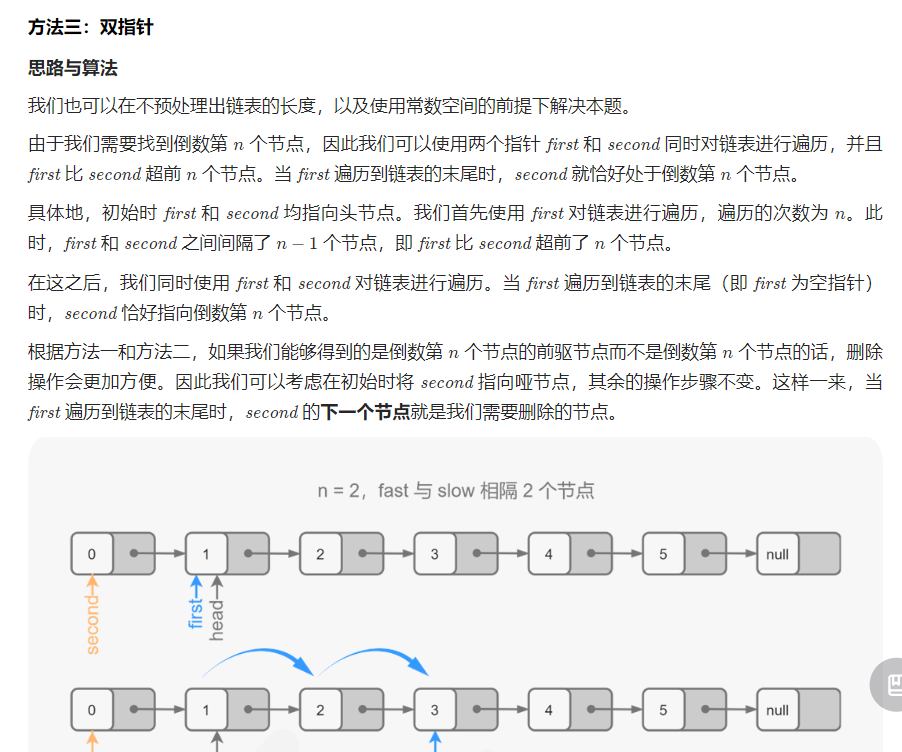
Solution3 快慢指针
20. 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = “()”
输出:true
示例 2:
输入:s = “()[]{}”
输出:true
示例 3:
输入:s = “(]”
输出:false
示例 4:
输入:s = “([)]”
输出:false
示例 5:
输入:s = “{[]}”
输出:true
Solution1 栈
class Solution {
public:
bool isValid(string s) {
stack<char> st; //taking stack for keep tracking the order of the brackets..
for(auto i:s) //iterate over each and every elements
{
if(i=='(' or i=='{' or i=='[') st.push(i); //if current element of the string will be opening bracket then we will just simply push it into the stack
else //if control comes to else part, it means that current element is a closing bracket, so check two conditions current element matches with top of the stack and the stack must not be empty...
{
if(st.empty() or (st.top()=='(' and i!=')') or (st.top()=='{' and i!='}') or (st.top()=='[' and i!=']')) return false;
st.pop(); //if control reaches to that line, it means we have got the right pair of brackets, so just pop it.
}
}
return st.empty(); //at last, it may possible that we left something into the stack unpair so return checking stack is empty or not..
}
};

26. 删除有序数组中的重复项
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = […]; // 输入数组
int[] expectedNums = […]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 升序 排列
Solution1 暴力
Solution2 双指针
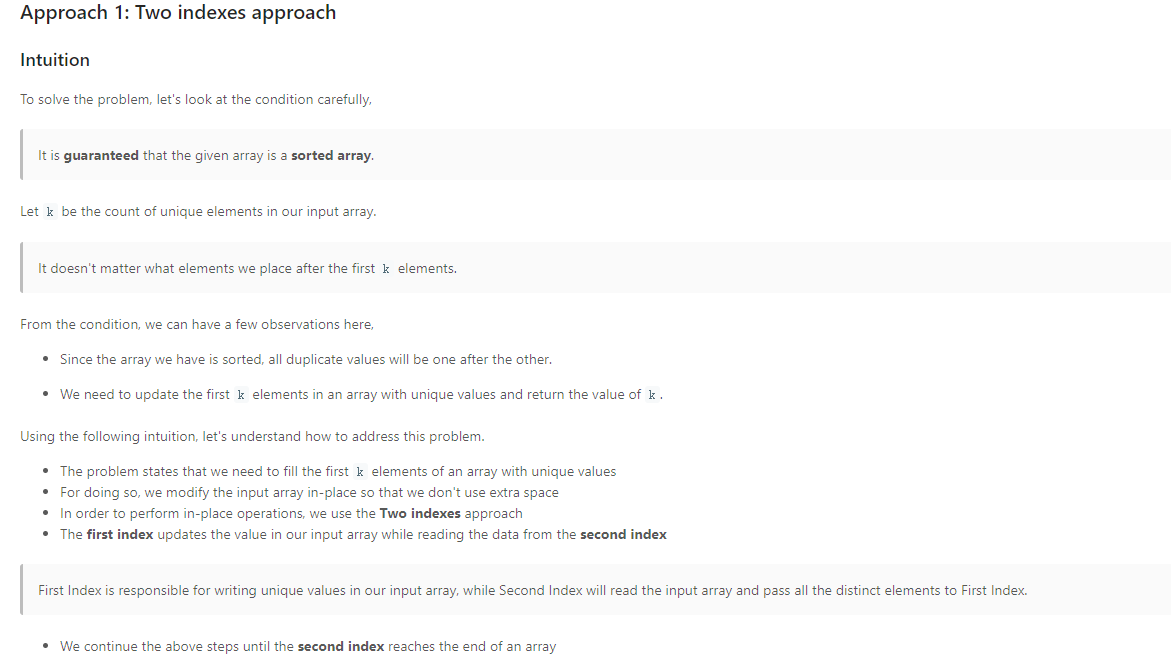


Solution3 双指针 优化
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
Solution1 暴力
Solution2


48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
提示:
n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000
Solution1 原地查找
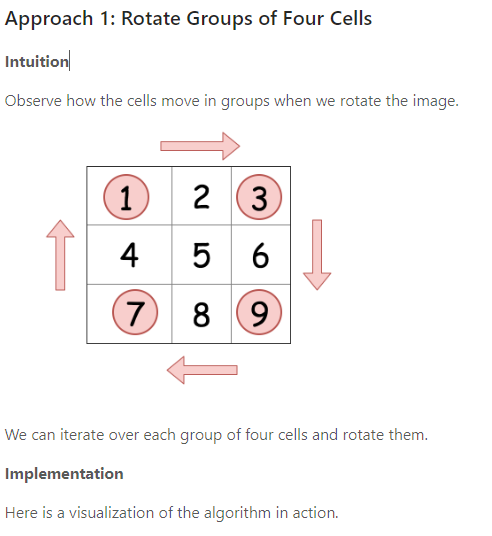
Solution2 先转置再竖直对称反转

class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
//先转置
for(int row=0;row<=matrix.size()-1;row++){
for(int col=row;col<=matrix[0].size()-1;col++){
swap(matrix[row][col],matrix[col][row]);
}
}
//在竖直对称翻转
for(int row=0;row<=matrix.size()-1;row++){
for(int col = 0;col<=(matrix.size()-1)/2;col++){
swap(matrix[row][col],matrix[row][matrix.size()-1-col]);
}
}
}
};
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
示例 1:
输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,“tan”],[“ate”,“eat”,“tea”]]
示例 2:
输入: strs = [“”]
输出: [[“”]]
示例 3:
输入: strs = [“a”]
输出: [[“a”]]
提示:
1 <= strs.length <= 104
0 <= strs[i].length <= 100
strs[i] 仅包含小写字母
Solution1 Map
Use an unordered_map to group the strings by their sorted counterparts. Use the sorted string as the key and all anagram strings as the value.
Moreover, since the string only contains lower-case alphabets, we can sort them using counting sort to improve the time complexity.
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
map<string,vector<string>>res;
//遍历
for(auto val:strs){
string tmp=val;
//以排序后的str作为key vector<string>作为value 放进map
sort(val.begin(),val.end());
if(res.find(val)==res.end()){
vector<string> t={tmp};
res.insert({val,t});
}else{
res[val].push_back(tmp);
}
}
//遍历输出结果
vector<vector<string>> result;
for(auto p:res){
result.push_back(p.second);
}
return result;
}
};
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100
spiral-matrix
Algorithm:
First we will iterate in to first row from left to right push back all the elements into a vector. After iterating, we change the top to second row (top++).
Then we will iterate from new top to bottom and push back only right most elements of each row. After iterating, we change the right to second last column (right--).
Then we will iterate in bottom row from right to left and pushback all the elements from new right to left. After iterating, we change the bottom to second last row (bottom--).
Then we will iterate from new bottom to new top and push back only left most element. After iterating, we change the left to second column (left++).
Repeat all these steps until left = right and top = bottom.
Solution1 原地遍历
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
if(matrix.empty()){return res;}
int s=0,x=matrix.size()-1,z=0,y=matrix[0].size()-1;
while(true){
//在上边沿
for(int i=s,j=z;j<=y;j++){
res.push_back(matrix[i][j]);
}
if(++s>x) break;
//在右边沿
for(int i=s,j=y;i<=x;i++){
res.push_back(matrix[i][j]);
}
if(--y<z) break;
//在下边沿
for(int i=x,j=y;j>=z;j--){
res.push_back(matrix[i][j]);
}
if(--x<s) break;
//在左边沿
for(int i=x,j=z;i>=s;i--){
res.push_back(matrix[i][j]);
}
if(++z>y) break;
}
return res;
}
};
Solution2 按层遍历

class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return {};
}
int rows = matrix.size(), columns = matrix[0].size();
vector<int> order;
int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {
order.push_back(matrix[top][column]);
}
for (int row = top + 1; row <= bottom; row++) {
order.push_back(matrix[row][right]);
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {
order.push_back(matrix[bottom][column]);
}
for (int row = bottom; row > top; row--) {
order.push_back(matrix[row][left]);
}
}
left++;
right--;
top++;
bottom--;
}
return order;
}
};
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104
nitially sort the array and then push the first element into the answer for speculation.
We have two condition if the first elements second part of ans array is greater than or equal to the second element first part of the
interval array.
The other condition we have to tackle is what if its not? then we push the particular element into the ans array which will be then be under speculation.
interval: [[1,3],[2,6],[8,10],[15,18]]
i
We initally push the 1st element into the ans array:
ans=[[1,3]]
j j points to the latest pushed element
Then we i is incremented.
[[1,3],[2,6],[8,10],[15,18]]
i
Now the ans[j][1]>interval[i][0] this means there is a possiblity of merging so we merger them
Remember the way we merge is to take the second element as max(ans[j][1],interval[i][1])
cuz imagine we have this
[1,7][2,4] --->merge should be ---->[1,7]
ans=[[1,6]]
then we move i forward
[[1,3],[2,6],[8,10],[15,18]]
i
Since ans[j][1]<interval[i][0] thus not contributing to the merge.
Thus we will push this into the ans array and speculate.
ans=[[1,6][8,10]]
j <----j is moved forward
i is moved forward
[[1,3],[2,6],[8,10],[15,18]]
i
Since ans[j][1]<interval[i][0] thus not contributing to the merge.
ans=[[1,6][8,10][15,18]]
j
Thus yielding our final answer.
vector<vector<int>> merge(vector<vector<int>>& interval) {
vector<vector<int>> ans;
if(interval.size()==0)return ans;
sort(interval.begin(),interval.end());
ans.push_back(interval[0]);
int j=0;
for(int i=1;i<interval.size();i++)
{
if(ans[j][1]>=interval[i][0])
ans[j][1]=max(ans[j][1],interval[i][1]);
else
{
j++;
ans.push_back(interval[i]);
}
}
return ans;
}
Solution1 排序

复杂度分析
时间复杂度:O(n\log n)O(nlogn),其中 nn 为区间的数量。除去排序的开销,我们只需要一次线性扫描,所以主要的时间开销是排序的 O(n\log n)O(nlogn)。
空间复杂度:O(\log n)O(logn),其中 nn 为区间的数量。这里计算的是存储答案之外,使用的额外空间。O(\log n)O(logn) 即为排序所需要的空间复杂度。
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size() == 0) {
return {};
}
sort(intervals.begin(), intervals.end());
vector<vector<int>> merged;
for (int i = 0; i < intervals.size(); ++i) {
int L = intervals[i][0], R = intervals[i][1];
if (!merged.size() || merged.back()[1] < L) {
merged.push_back({L, R});
}
else {
merged.back()[1] = max(merged.back()[1], R);
}
}
return merged;
}
};
61. 旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例 2:
输入:head = [0,1,2], k = 4
输出:[2,0,1]
提示:
链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 109
There is no trick for this problem. Some people used slow/fast pointers to find the tail node but I don't see the benefit (in the sense that it doesn't reduce the pointer move op) to do so. So I just used one loop to find the length first.
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if(!head) return head;
int len=1; // number of nodes
ListNode *newH, *tail;
newH=tail=head;
while(tail->next) // get the number of nodes in the list
{
tail = tail->next;
len++;
}
tail->next = head; // circle the link
if(k %= len)
{
for(auto i=0; i<len-k; i++) tail = tail->next; // the tail node is the (len-k)-th node (1st node is head)
}
newH = tail->next;
tail->next = NULL;
return newH;
}
};
Solution1 暴力
Soluion2 闭环

66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123。
示例 2:
输入:digits = [4,3,2,1]
输出:[4,3,2,2]
解释:输入数组表示数字 4321。
示例 3:
输入:digits = [0]
输出:[1]
提示:
1 <= digits.length <= 100
0 <= digits[i] <= 9
My solution is nothing special and isn't clever at all. I decided to post it since I thought the "official" solution article from leetcode was very poorly written and confused me more, even after I solved it on my own.
So, I believe my comments below should explain the idea, but I want to add that it helps to test the more obscure test cases for this problem to understand the algorithm. For example:
[9]
[9090]
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
int n = digits.size() - 1;
for (int i = n; i >= 0; --i) { // traverse digits from the last element (least significant)
// since we begin with the last digit, increasing that digit by one
// results in overflow. Therefore, all elements PRIOR to digits[0]
// need to be considered since there may be additional nines between
// digits[0], ... , digits[n].
if (digits[i] == 9) {
digits[i] = 0;
} else { // current digit is not 9 so we can safely increment by one
digits[i] += 1;
return digits;
}
}
// if the program runs to this point, each 9 is now a 0.
// to get a correct solution, we need to add one more element with
// a value of zero AND set digits[0] to 1 (in the most significant position)
// to account for the carry digit.
digits.push_back(0);
digits[0] = 1;
return digits;
}
};
Solution 0 暴力
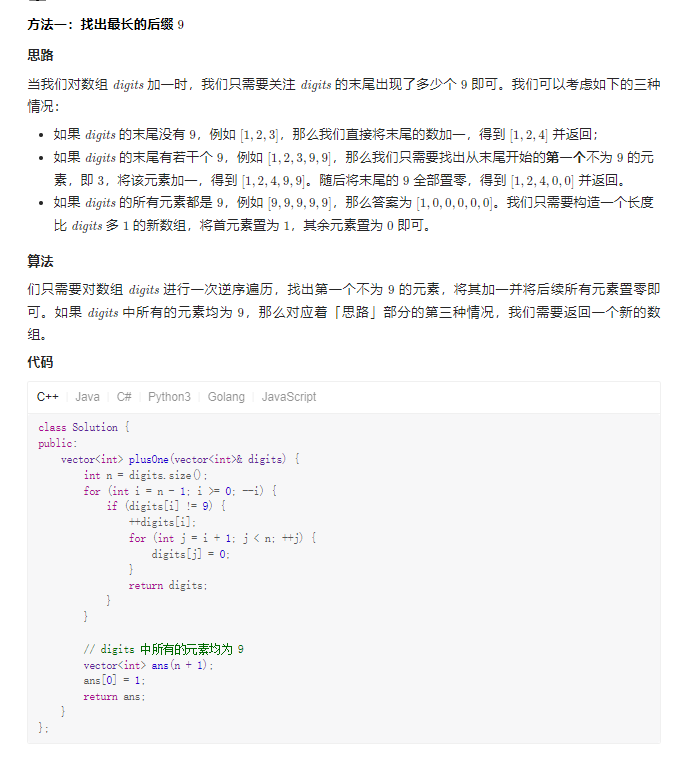
Solution 1 逆序遍历 找到9
75. 颜色分类
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
提示:
n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2
进阶:
你可以不使用代码库中的排序函数来解决这道题吗?
你能想出一个仅使用常数空间的一趟扫描算法吗?
The solution requires the use of tracking 3 positions, the Low, Mid and High.
We assume that the mid is the "Unknown" area that we must evaluate.
If we encounter a 0, we know that it will be on the low end of the array, and if we encounter a 2, we know it will be on the high end of the array.
To achieve this in one pass without preprocessing (counting), we simply traverse the unknown will generating the low and high ends.
Take this example:
Assume our input is: 1 0 2 2 1 0 (short for simplicity).
Running the algorithm by hand would look something like:
1 0 2 2 1 0
^ ^
L H
M
Mid != 0 || 2
Mid++
1 0 2 2 1 0
^ ^ ^
L M H
Mid == 0
Swap Low and Mid
Mid++
Low++
0 1 2 2 1 0
^ ^ ^
L M H
Mid == 2
Swap High and Mid
High--
0 1 0 2 1 2
^ ^ ^
L M H
Mid == 0
Swap Low and Mid
Mid++
Low++
0 0 1 2 1 2
^ ^ ^
L M H
Mid == 2
Swap High and Mid
High--
0 0 1 1 2 2
^ ^
L M
H
Mid <= High is our exit case
Solution1 暴力
根据题目中的提示,我们可以统计出数组中 0, 1, 20,1,2 的个数,再根据它们的数量,重写整个数组。这种方法较为简单,也很容易想到,而本题解中会介绍两种基于指针进行交换的方法。
Solution2 单指针
我们可以考虑对数组进行两次遍历。在第一次遍历中,我们将数组中所有的 00 交换到数组的头部。在第二次遍历中,我们将数组中所有的 11 交换到头部的 00 之后。此时,所有的 22 都出现在数组的尾部,这样我们就完成了排序。
具体地,我们使用一个指针 \textit{ptr}ptr 表示「头部」的范围,\textit{ptr}ptr 中存储了一个整数,表示数组 \textit{nums}nums 从位置 00 到位置 \textit{ptr}-1ptr−1 都属于「头部」。\textit{ptr}ptr 的初始值为 00,表示还没有数处于「头部」。
在第一次遍历中,我们从左向右遍历整个数组,如果找到了 00,那么就需要将 00 与「头部」位置的元素进行交换,并将「头部」向后扩充一个位置。在遍历结束之后,所有的 00 都被交换到「头部」的范围,并且「头部」只包含 00。
在第二次遍历中,我们从「头部」开始,从左向右遍历整个数组,如果找到了 11,那么就需要将 11 与「头部」位置的元素进行交换,并将「头部」向后扩充一个位置。在遍历结束之后,所有的 11 都被交换到「头部」的范围,并且都在 00 之后,此时 22 只出现在「头部」之外的位置,因此排序完成。
class Solution {
public:
void sortColors(vector<int>& nums) {
int n = nums.size();
int ptr = 0;
for (int i = 0; i < n; ++i) {
if (nums[i] == 0) {
swap(nums[i], nums[ptr]);
++ptr;
}
}
for (int i = ptr; i < n; ++i) {
if (nums[i] == 1) {
swap(nums[i], nums[ptr]);
++ptr;
}
}
}
};
Solution3 双指针

class Solution {
public:
void sortColors(vector<int>& nums) {
int n = nums.size();
int p0 = 0, p2 = n - 1;
for (int i = 0; i <= p2; ++i) {
while (i <= p2 && nums[i] == 2) {
swap(nums[i], nums[p2]);
--p2;
}
if (nums[i] == 0) {
swap(nums[i], nums[p0]);
++p0;
}
}
}
};
83. 删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例 1:
输入:head = [1,1,2]
输出:[1,2]
示例 2:
输入:head = [1,1,2,3,3]
输出:[1,2,3]
提示:
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列
noticed that the solutions posted here are too long and complicated. They use unnecessary variables and/or checks etc.
The solution can be much more concise. Here is my solution:
class Solution {
public:
ListNode *deleteDuplicates(ListNode *head) {
ListNode* cur = head;
while (cur) {
while (cur->next && cur->val == cur->next->val)
cur->next = cur->next->next;
cur = cur->next;
}
return head;
}
};
Note about freeing memory. We need to free memory when we delete a node. But don't use delete node; construct on an interview without discussing it with the interviewer. A list node can be allocated in many different ways and we can use delete node; only if we are sure that the nodes were allocated with new TreeNode(...);.
Solution1 一次遍历
方法一:一次遍历
思路与算法
由于给定的链表是排好序的,因此重复的元素在链表中出现的位置是连续的,因此我们只需要对链表进行一次遍历,就可以删除重复的元素。
具体地,我们从指针 \textit{cur}cur 指向链表的头节点,随后开始对链表进行遍历。如果当前 \textit{cur}cur 与 \textit{cur.next}cur.next 对应的元素相同,那么我们就将 \textit{cur.next}cur.next 从链表中移除;否则说明链表中已经不存在其它与 \textit{cur}cur 对应的元素相同的节点,因此可以将 \textit{cur}cur 指向 \textit{cur.next}cur.next。
当遍历完整个链表之后,我们返回链表的头节点即可。
细节
当我们遍历到链表的最后一个节点时,\textit{cur.next}cur.next 为空节点,如果不加以判断,访问 \textit{cur.next}cur.next 对应的元素会产生运行错误。因此我们只需要遍历到链表的最后一个节点,而不需要遍历完整个链表。
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是链表的长度。
空间复杂度:O(1)O(1)。
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if (!head) {
return head;
}
ListNode* cur = head;
while (cur->next) {
if (cur->val == cur->next->val) {
cur->next = cur->next->next;
}
else {
cur = cur->next;
}
}
return head;
}
};
86. 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2
输出:[1,2]
提示:
链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200
Approach 1: Two Pointer Approach
Intuition
We can take two pointers before and after to keep track of the two linked lists as described above. These two pointers could be used two create two separate lists and then these lists could be combined to form the desired reformed list.
Algorithm
Initialize two pointers before and after. In the implementation we have initialized these two with a dummy ListNode. This helps to reduce the number of conditional checks we would need otherwise. You can try an implementation where you don't initialize with a dummy node and see it yourself!
Dummy Node Initialization
Iterate the original linked list, using the head pointer.
If the node's value pointed by head is lesser than x, the node should be part of the before list. So we move it to before list.
Else, the node should be part of after list. So we move it to after list.
Once we are done with all the nodes in the original linked list, we would have two list before and after. The original list nodes are either part of before list or after list, depending on its value.
Note: Since we traverse the original linked list from left to right, at no point would the order of nodes change relatively in the two lists. Another important thing to note here is that we show the original linked list intact in the above diagrams. However, in the implementation, we remove the nodes from the original linked list and attach them in the before or after list. We don't utilize any additional space. We simply move the nodes from the original list around.
Now, these two lists before and after can be combined to form the reformed list.
We did a dummy node initialization at the start to make implementation easier, you don't want that to be part of the returned list, hence just move ahead one node in both the lists while combining the two list. Since both before and after have an extra node at the front.
Solution1 双指针

88. 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
This code relies on the simple observation that once all of the numbers from nums2 have been merged into nums1, the rest of the numbers in nums1 that were not moved are already in the correct place.
The way to think about the solution is that we will have to do a reverse sorting.
We initialize k=m+n-1 as that will be the last location of nums1.
We will keep checking for the greater element of the two arrays(i=m-1,j=n-1) and insert the values.
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
nums1 = [1,2,3,0,0,0]
| |
i k
nums2 = [2,5,6]
|
j
nums2[j]>nums1[i] thus nums1[k]=6
k and j are decremented.
nums1 = [1,2,3,0,0,6]
| |
i k
nums2 = [2,5,6]
|
j
nums2[j]>nums1[i] thus nums1[k]=5
k and j are decremented.
nums1 = [1,2,3,0,5,6]
| |
i k
nums2 = [2,5,6]
|
j
We keep following up this procedure and we get the desired reult.
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i=m-1,j=n-1,k=m+n-1;
while(i>=0&&j>=0)
{
if(nums1[i]>nums2[j])
{
nums1[k]=nums1[i];
i--;
k--;
}
else
{
nums1[k]=nums2[j];
j--;
k--;
}
}
while(i>=0)
nums1[k--]=nums1[i--];
while(j>=0)
nums1[k--]=nums2[j--];
}
Solution1 暴力直接合并后排序
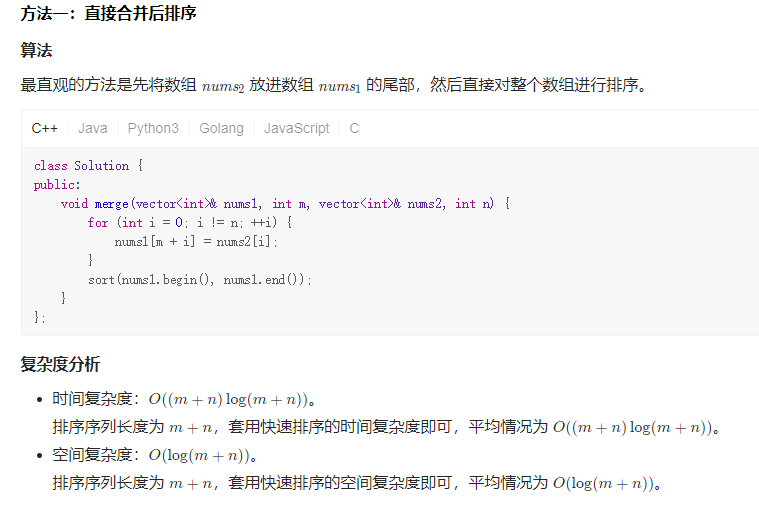
Solution2 双指针

class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1 = 0, p2 = 0;
int sorted[m + n];
int cur;
while (p1 < m || p2 < n) {
if (p1 == m) {
cur = nums2[p2++];
} else if (p2 == n) {
cur = nums1[p1++];
} else if (nums1[p1] < nums2[p2]) {
cur = nums1[p1++];
} else {
cur = nums2[p2++];
}
sorted[p1 + p2 - 1] = cur;
}
for (int i = 0; i != m + n; ++i) {
nums1[i] = sorted[i];
}
}
};
复杂度分析
时间复杂度:O(m+n)O(m+n)。
指针移动单调递增,最多移动 m+nm+n 次,因此时间复杂度为 O(m+n)O(m+n)。
空间复杂度:O(m+n)O(m+n)。
需要建立长度为 m+nm+n 的中间数组 \textit{sorted}sorted。
Solution3 逆向双指针

class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int p1 = m - 1, p2 = n - 1;
int tail = m + n - 1;
int cur;
while (p1 >= 0 || p2 >= 0) {
if (p1 == -1) {
cur = nums2[p2--];
} else if (p2 == -1) {
cur = nums1[p1--];
} else if (nums1[p1] > nums2[p2]) {
cur = nums1[p1--];
} else {
cur = nums2[p2--];
}
nums1[tail--] = cur;
}
}
};
92. 反转链表 II
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
提示:
链表中节点数目为 n
1 <= n <= 500
-500 <= Node.val <= 500
1 <= left <= right <= n
进阶: 你可以使用一趟扫描完成反转吗?
Solution1 原地反转
Algorithm
We define a recursion function that will do the job of reversing a portion of the linked list.
Let's call this function recurse. The function takes in 3 parameters: m being the starting point of the reversal, n being the ending point for the reversal, and a pointer right which will start at the n^{th}n
th
node in the linked list and move backwards with the backtracking of the recursion. If this is not clear at the moment, the diagrams that follow will help.
Additionally, we have a pointer called left which starts from the m^{th}m
th
node in the linked list and moves forward. In Python, we have to take a global variable for this which get's changed with recursion. In other languages, where changes made in function calls persist, we can consider this pointer as an additional variable for the function recurse.
In a recursion call, given m, n, and right, we check if n == 1. If this is the case, we don't need to go any further.
Until we reach n = 1, we keep moving the right pointer one step forward and after doing that, we make a recursive call with the value of n decreased by 1. At the same time, we keep on moving the left pointer forward until m == 1. When we refer to a pointer being moved forward, it essentially means pointer.next.
So we backtrack as soon as n reaches 1. At that point of time, the right pointer is at the last node of the sublist we want to reverse and the left has already reached the first node of this sublist. So, we swap out the data and move the left pointer one step forward using left = left.next. We need this change to persist across the backtracking process.
From there on, every time we backtrack, the right pointer moves one step backwards. This is the simulation we've been mentioning all along. The backward movement is simulated by backtracking.
We stop the swaps when either right == left, which happens if the sublist size is odd, or, right.next == left which happens when during the backtracking process for an even sized sublist, the right pointer crosses left. We use a global boolean flag for stopping the swaps once these conditions are met.
Let's look at a series of diagrams explaining the process on a sample linked list. Hopefully, things would be clearer after this.
This is the first step in the recursion process. We have a list given to us and the left and the right pointers start off from the head of the linked list. The first step makes a recursive call with updated values of m and n i.e. their values each reduced by 1. Also, the left and the right pointers move one step forward in the linked list.
The next two steps show the movement of the left and the right pointers in the list. Notice that after the second step, the left pointer reaches it's designated spot. So, we don't move it any further. Only the right pointer progresses from here on out until it reaches node 6.
As we can see, after the step 5, both the pointers are in their designated spots in the list and we can start the backtracking process. We don't recurse further. The operation performed during the backtracking is swapping of data between the left and right nodes.
The right pointer crosses the left pointer after step 3 (backtracking) as can be seen above and by that point, we have already reversed the required portion of the linked list. We needed the output list to be [7 → 9 → 8 → 1 → 10 → 2 → 6] and that's what we have. So, we don't perform any more swaps and in the code, we can use a global boolean flag to stop the swapping after a point. We can't really break out of recursion per say.

118. 杨辉三角
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
The pascal triangle problem has a very simple and intuitive dynamic programming approach. As the definition states, every element of a row is formed by the sum of the two numbers directly above. So, we can just apply DP and use the previously stored rows of trianlge to calculate the new rows.
We can just initialize the start and end elements of each row as 1 and update only the elements between them. This will make the code simpler and avoid the need of having extra checks for edge elements of each row.
Solution1 直接求解
lass Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> yanghui;
for (int i = 0; i < numRows; i++)
{
vector<int> data(i + 1);
yanghui.push_back(data);
for (int j = 0; j < i; ++j)
{
if(j == 0) yanghui[i][j] = 1;
else
{
yanghui[i][j] = yanghui[i - 1][j - 1] + yanghui[i - 1][j];
}
}
yanghui[i][yanghui[i].size() - 1] = 1;
}
return yanghui;
}
};
125. 验证回文串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个回文串。
字母和数字都属于字母数字字符。
给你一个字符串 s,如果它是回文串,返回 true ;否则,返回 false 。
示例 1:
输入: “A man, a plan, a canal: Panama”
输出:true
解释:“amanaplanacanalpanama” 是回文串。
示例 2:
输入:“race a car”
输出:false
解释:“raceacar” 不是回文串。
示例 3:
输入:s = " "
输出:true
解释:在移除非字母数字字符之后,s 是一个空字符串 “” 。
由于空字符串正着反着读都一样,所以是回文串。
提示:
1 <= s.length <= 2 * 105
s 仅由可打印的 ASCII 字符组成
bool isPalindrome(string s) {
for (int i = 0, j = s.size() - 1; i < j; i++, j--) { // Move 2 pointers from each end until they collide
while (isalnum(s[i]) == false && i < j) i++; // Increment left pointer if not alphanumeric
while (isalnum(s[j]) == false && i < j) j--; // Decrement right pointer if no alphanumeric
if (toupper(s[i]) != toupper(s[j])) return false; // Exit and return error if not match
}
return true;
}
Solution1 筛选 + 判断
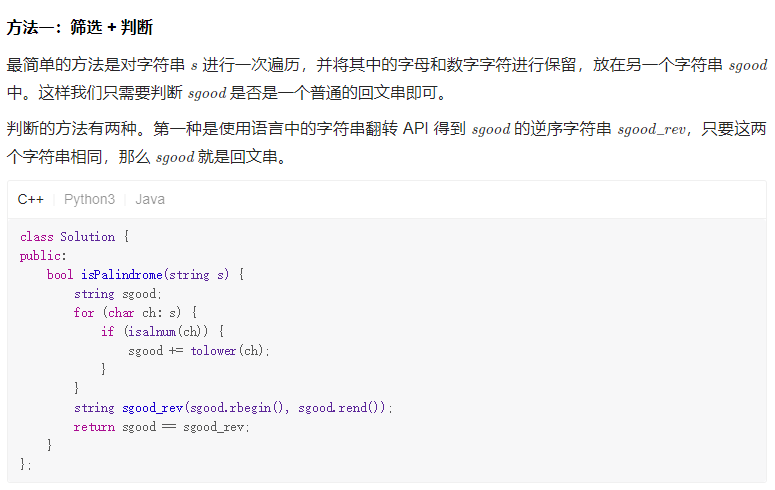
Solution2 筛选 + 判断 02

Solution03 在原字符串上直接判断
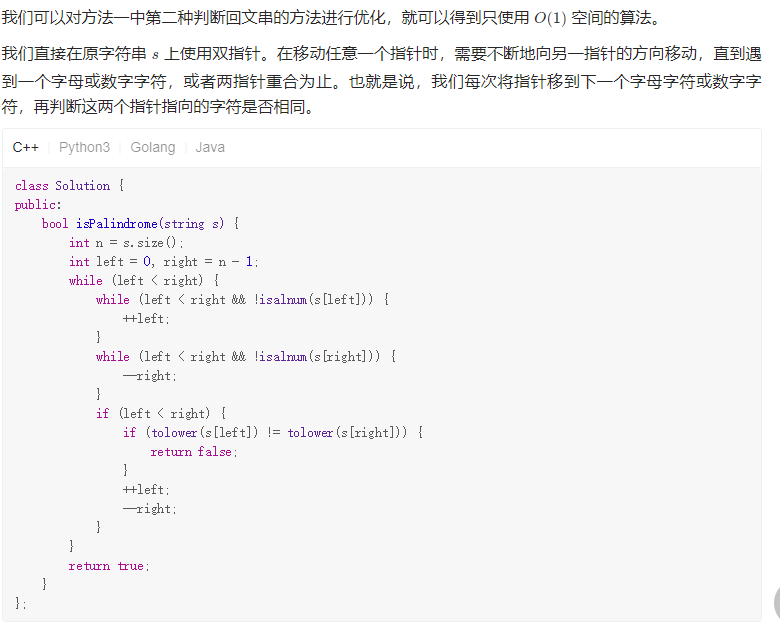
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
Solution1 哈希表
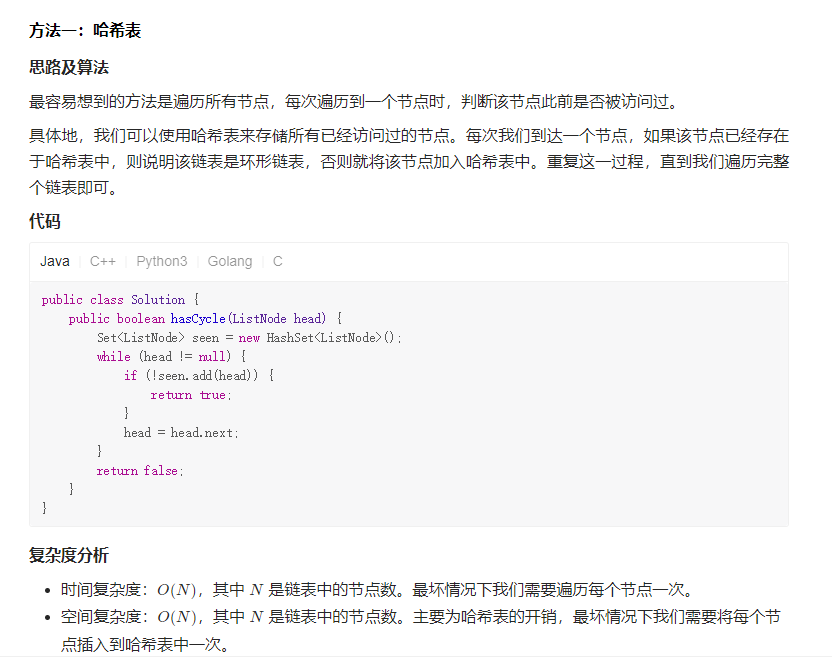
Solution2



142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引
Alogrithm Description:
Step 1: Determine whether there is a cycle
1.1) Using a slow pointer that move forward 1 step each time
1.2) Using a fast pointer that move forward 2 steps each time
1.3) If the slow pointer and fast pointer both point to the same location after several moving steps, there is a cycle;
1.4) Otherwise, if (fast->next == NULL || fast->next->next == NULL), there has no cycle.
Step 2: If there is a cycle, return the entry location of the cycle
2.1) L1 is defined as the distance between the head point and entry point
2.2) L2 is defined as the distance between the entry point and the meeting point
2.3) C is defined as the length of the cycle
2.4) n is defined as the travel times of the fast pointer around the cycle When the first encounter of the slow pointer and the fast pointer
According to the definition of L1, L2 and C, we can obtain:
the total distance of the slow pointer traveled when encounter is L1 + L2
the total distance of the fast pointer traveled when encounter is L1 + L2 + n * C
Because the total distance the fast pointer traveled is twice as the slow pointer, Thus:
2 * (L1+L2) = L1 + L2 + n * C => L1 + L2 = n * C => L1 = (n - 1) C + (C - L2)*
It can be concluded that the distance between the head location and entry location is equal to the distance between the meeting location and the entry location along the direction of forward movement.
So, when the slow pointer and the fast pointer encounter in the cycle, we can define a pointer "entry" that point to the head, this "entry" pointer moves one step each time so as the slow pointer. When this "entry" pointer and the slow pointer both point to the same location, this location is the node where the cycle begins.
Solution1 哈希表
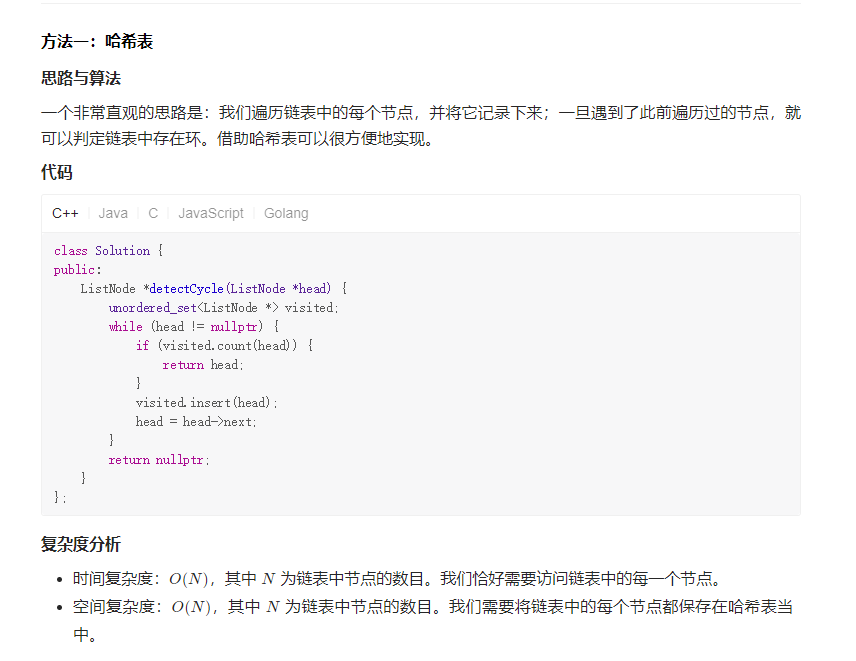
Solution2 双指针

class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while (fast != nullptr) {
slow = slow->next;
if (fast->next == nullptr) {
return nullptr;
}
fast = fast->next->next;
if (fast == slow) {
ListNode *ptr = head;
while (ptr != slow) {
ptr = ptr->next;
slow = slow->next;
}
return ptr;
}
}
return nullptr;
}
};

143. 重排链表
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
输入:head = [1,2,3,4]
输出:[1,4,2,3]
示例 2:
输入:head = [1,2,3,4,5]
输出:[1,5,2,4,3]
提示:
链表的长度范围为 [1, 5 * 104]
1 <= node.val <= 1000
If you never solved singly linked lists problems before, or you do not have a lot of experience, this problem can be quite difficult. However if you already know all the tricks, it is not difficult at all. Let us first try to understand what we need to do. For list [1,2,3,4,5,6,7] we need to return [1,7,2,6,3,5,4]. We can note, that it is actually two lists [1,2,3,4] and [7,6,5], where elements are interchange. So, to succeed we need to do the following steps:
Find the middle of or list - be careful, it needs to work properly both for even and for odd number of nodes. For this we can either just count number of elements and then divide it by to, and do two traversals of list. Or we can use slow/fast iterators trick, where slow moves with speed 1 and fast moves with speed 2. Then when fast reches the end, slow will be in the middle, as we need.
Reverse the second part of linked list. Again, if you never done it before, it can be quite painful, please read oficial solution to problem 206. Reverse Linked List. The idea is to keep three pointers: prev, curr, nextt stand for previous, current and next and change connections in place. Do not forget to use slow.next = None, in opposite case you will have list with loop.
Finally, we need to merge two lists, given its heads. These heads are denoted by head and prev, so for simplisity I created head1 and head2 variables. What we need to do now is to interchange nodes: we put head2 as next element of head1 and then say that head1 is now head2 and head2 is previous head1.next. In this way we do one step for one of the lists and rename lists, so next time we will take element from head2, then rename again and so on.
Complexity: Time complexity is O(n), because we first do O(n) iterations to find middle, then we do O(n) iterations to reverse second half and finally we do O(n) iterations to merge lists. Space complexity is O(1).
Solution0 暴力
Solution1 双指针
1.快慢指针找到中点 2.拆成两个链表 3.遍历两个链表,后面的塞到前面的“缝隙里”
void reorderList(ListNode* head) {
if(head==NULL || head->next == NULL)
return;
//快慢指针分出两段
ListNode *slow = head,*fast = head;
while(fast->next && fast->next->next){
slow = slow->next;
fast = fast->next->next;
}
//后端反转
ListNode *needReverser = slow->next;
slow->next = NULL;
needReverser = reverse(needReverser);
//插入前端缝隙
ListNode *cur = head;
while(cur && needReverser){
ListNode *curSecond = needReverser;
needReverser = needReverser->next;
ListNode *nextCur = cur->next;
curSecond->next = cur->next;
cur->next = curSecond;
cur = nextCur;
}
}
ListNode *reverse(ListNode *head){
ListNode *p1 = NULL;
ListNode *p2 = head;
ListNode *p3 = p2;
while(p2){
p3 = p2->next;
p2->next = p1;
p1 = p2;
p2 = p3;
}
return p1;
}
146. LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put
n this question we have to keep track of the most least recently used item in the cache. I have designed the cache using list and map in C++.
We do it by following the steps below :-
When we access an item in the cache it moves to the front of the list as it is the most recently used item.
When we want to remove an item we remove it from the last of the list as it is the least recently used item in the cache.
When we insert an item we insert it into the front of the list as it is the most recently used item.
The idea is to store the keys in the map and its corrosponding values into the list...
Note : splice() function here takes the element at the m[key] and places it at the beginning of the list...
Solution1 哈希表 + 双向链表
方法一:哈希表 + 双向链表
算法
LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 O(1)O(1) 的时间内完成 get 或者 put 操作。具体的方法如下:
对于 get 操作,首先判断 key 是否存在:
如果 key 不存在,则返回 -1−1;
如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 O(1)O(1),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)O(1)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 O(1)O(1) 时间内完成。
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
分治:148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
链表中节点的数目在范围 [0, 5 * 104] 内
-105 <= Node.val <= 105
Brief note about Question-
We have to return the linked list after sorting it in ascending order.
Let's take an example not given in question -
Suppose head of linked list given to us is like, head: [3,-9,8,67,9]
then answer should like [-9,3,8,9,67] after sorting it in ascending order.
Solution - I (Using Merge sort, Accepted)-
We want to sort a linked list, then we may able to use any of the sorting algorithm and then apply on it.
We will use merge sort here, because I find it easy to implement in linked list.
Whole implementation totally based on the merge sort, so i strongly suggest you to read a article on the merge sort.
Some basic thing that we will do in applying merge sort on our linked list are-
We divide our linked liist into two equal parts until when only one element is left.
After that we start merge them on the basis of value.
Now, if we divide them into two equal parts then then how we will find mid in linked list.
We find mid of linked list using tortise and hare method or say using fast and slow pointer.
See commented code for more explanation.
Solution1 自顶向下归并排序

class Solution {
public:
ListNode* sortList(ListNode* head) {
return sortList(head, nullptr);
}
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid = slow;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
Solution2 自底向上归并排序

class Solution {
public:
ListNode* sortList(ListNode* head) {
if (head == nullptr) {
return head;
}
int length = 0;
ListNode* node = head;
while (node != nullptr) {
length++;
node = node->next;
}
ListNode* dummyHead = new ListNode(0, head);
for (int subLength = 1; subLength < length; subLength <<= 1) {
ListNode* prev = dummyHead, *curr = dummyHead->next;
while (curr != nullptr) {
ListNode* head1 = curr;
for (int i = 1; i < subLength && curr->next != nullptr; i++) {
curr = curr->next;
}
ListNode* head2 = curr->next;
curr->next = nullptr;
curr = head2;
for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
curr = curr->next;
}
ListNode* next = nullptr;
if (curr != nullptr) {
next = curr->next;
curr->next = nullptr;
}
ListNode* merged = merge(head1, head2);
prev->next = merged;
while (prev->next != nullptr) {
prev = prev->next;
}
curr = next;
}
}
return dummyHead->next;
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = [“2”,“1”,“+”,“3”,“*”]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = [“4”,“13”,“5”,“/”,“+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = [“10”,“6”,“9”,“3”,“+”,“-11”,““,”/“,””,“17”,“+”,“5”,“+”]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104
tokens[i] 是一个算符(“+”、“-”、“*” 或 “/”),或是在范围 [-200, 200] 内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。
逆波兰表达式主要有以下两个优点:
去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
Idea:
Reverse Polish Notation was designed specifically to make computing easier with the more efficient use of a stack. So we can use a stack here to store numbers until they're used, and then each operand will use the top two values of the stack.
Since the order of the numbers is still important for subtraction and division, we'll have to make sure that the two numbers are processed in their original order, which is the opposite order of the stack.
After each successful operation, the result should be pushed back onto the stack until it's used. After iteration is complete, the remaining value in the stack will be our answer, so we should return stack[0].
Time Complexity: O(N) where N is the length of tokens
Space Complexity: O(N) for the length of the stack, up to N / 2 + 1 values
Solution1 栈

class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> stk;
int n = tokens.size();
for (int i = 0; i < n; i++) {
string& token = tokens[i];
if (isNumber(token)) {
stk.push(atoi(token.c_str()));
} else {
int num2 = stk.top();
stk.pop();
int num1 = stk.top();
stk.pop();
switch (token[0]) {
case '+':
stk.push(num1 + num2);
break;
case '-':
stk.push(num1 - num2);
break;
case '*':
stk.push(num1 * num2);
break;
case '/':
stk.push(num1 / num2);
break;
}
}
}
return stk.top();
}
bool isNumber(string& token) {
return !(token == "+" || token == "-" || token == "*" || token == "/");
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是数组 \textit{tokens}tokens 的长度。需要遍历数组 \textit{tokens}tokens 一次,计算逆波兰表达式的值。
空间复杂度:O(n)O(n),其中 nn 是数组 \textit{tokens}tokens 的长度。使用栈存储计算过程中的数,栈内元素个数不会超过逆波兰表达式的长度。
Solution2 数组模拟栈

class Solution {
public:
int evalRPN(vector<string>& tokens) {
int n = tokens.size();
vector<int> stk((n + 1) / 2);
int index = -1;
for (int i = 0; i < n; i++) {
string& token = tokens[i];
if (token.length() > 1 || isdigit(token[0])) {
index++;
stk[index] = atoi(token.c_str());
} else {
switch (token[0]) {
case '+':
index--;
stk[index] += stk[index + 1];
break;
case '-':
index--;
stk[index] -= stk[index + 1];
break;
case '*':
index--;
stk[index] *= stk[index + 1];
break;
case '/':
index--;
stk[index] /= stk[index + 1];
break;
}
}
}
return stk[index];
}
};
171. Excel 表列序号
给你一个字符串 columnTitle ,表示 Excel 表格中的列名称。返回 该列名称对应的列序号 。
例如:
A -> 1
B -> 2
C -> 3
…
Z -> 26
AA -> 27
AB -> 28
…
示例 1:
输入: columnTitle = “A”
输出: 1
示例 2:
输入: columnTitle = “AB”
输出: 28
示例 3:
输入: columnTitle = “ZY”
输出: 701
提示:
1 <= columnTitle.length <= 7
columnTitle 仅由大写英文组成
columnTitle 在范围 [“A”, “FXSHRXW”] 内
1. There are 26 letters in our alphabet and we start counting from 1, not zero.
So 'Z' is 26.
2. The rest of the combinations start from a base 26
AA --> 26*1+ 1 = 27 (A == 1)
AB --> 26*1+ 2 = 28 (B == 2)
AC -->26*1 + 3 = 29 (C == 3)
.....
So we can write like this:
result = 0
d = s[i](char) - 'A' + 1 (we used s[i] - 'A' to convert the letter to a number like it's going to be C)
result = result* 26 + d
If the given input is only one letter, it will automatically take the value s[i] - 'A' + 1 as the first result is 0.
Some More Explanation
1. For every additional digit of the string, we multiply the value of the digit by 26^n
2. here n is the number of digits it is away from the one's place.
3. This is similar to how the number 254 could be broken down as this:
(2 x 10 x 10) + (5 x 10) + (4).
4. The reason we use 26 instead of 10 is because 26 is our base.
For s = "BCM" the final solution would be (2 x 26 x 26) + (3 x 26) + (13)
We could do this process iteratively. Start at looking at the first digit "B". Add the int equivalent of "B" to the running sum and continue.
Every time we look at the following digit multiply our running sum by 26 before adding the next digit to signify we are changing places. Example below:
"B" = 2
"BC" = (2)26 + 3
"BCM" = (2(26) + 3)26 + 13
Time Complexity : O(n) one scan of string , n is number of characters in the string
CODE WITH EXPLANATION
Solution1 26进制
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
示例 1:
输入:
[“MinStack”,“push”,“push”,“push”,“getMin”,“pop”,“top”,“getMin”]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1
pop、top 和 getMin 操作总是在 非空栈 上调用
push, pop, top, and getMin最多被调用 3 * 104 次
I came up with this simple solution using just a single stack.
Here I am using Stack of Pair of Int. The first value of the pair would store the element of the normal stack and the second value would store the minimum up to that point in the stack.
So even if the minimum element of the stack is removed from the top, we still have a backup of the next minimum element in the pair. So for every element pushed in the stack, it stores its corresponding minimum value.
For example, let's do a Dry Run of an example.
["MinStack","push","push","push","push","push","getMin","pop","pop","top","push","getMin"]
[[],[5],[-2],[3],[-10],[20],[],[],[],[],[30],[]]
We push 5,-2,3,-10,20 in the stack.
If the stack is empty we push {val,val} in the stack
else we push {val,min(s.top().second,val)} which is basically minimum upto that point.
Hence {5,5},{-2,-2},{3,-2},{-10,-10},{20,-10} are pushed in the stack.
To pop simply do stack.pop()
To get the top return stack.top().first;
Now we pop 20 and -10 from the stack
The elements in the stack would be {5,5},{-2,-2},{3,-2}
On pushing 30 to the stack
The elements in the stack would be {5,5},{-2,-2},{3,-2},{30,-2}.
The Output of the code would be:
[null,null,null,null,null,null,-10,null,null,3,null,-2]
All the operations are one liners expect the Push operation which is a 2 liner.
class MinStack {
public:
vector< pair<int,int> > s;
MinStack() { }
void push(int val) {
if(s.empty())
s.push_back({val,val});
else
s.push_back({val,min(s.back().second,val)});
}
void pop() { s.pop_back(); }
int top() { return s.back().first; }
int getMin() { return s.back().second; }
};
The Time complexity of each operation is O(1)
The Space complexity is O(N)
Solution1 辅助栈

Solution2 不用辅助栈

160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal - 相交的起始节点的值。如果不存在相交节点,这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中(从头节点开始)跳到交叉节点的节点数
skipB - 在 listB 中(从头节点开始)跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构,并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at ‘8’
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at ‘2’
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
提示:
listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点,intersectVal 为 0
如果 listA 和 listB 有交点,intersectVal == listA[skipA] == listB[skipB]
进阶:你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
O ( 1 ) SPACE SOLUTION
First using constant space check for last element of both lists.
If tails of both lists are different then return NULL
Now we know that intersection length will be same for both lists. So we want to make length prior to the intersection also equal.
Head pointer of the longer list is moved to next till length of both lists become equal
NOW we will have intersetion point at the same distance from head for both the lists.
Now keep comparing heads till match found.
Solution1 哈希集合
Solution2 双指针


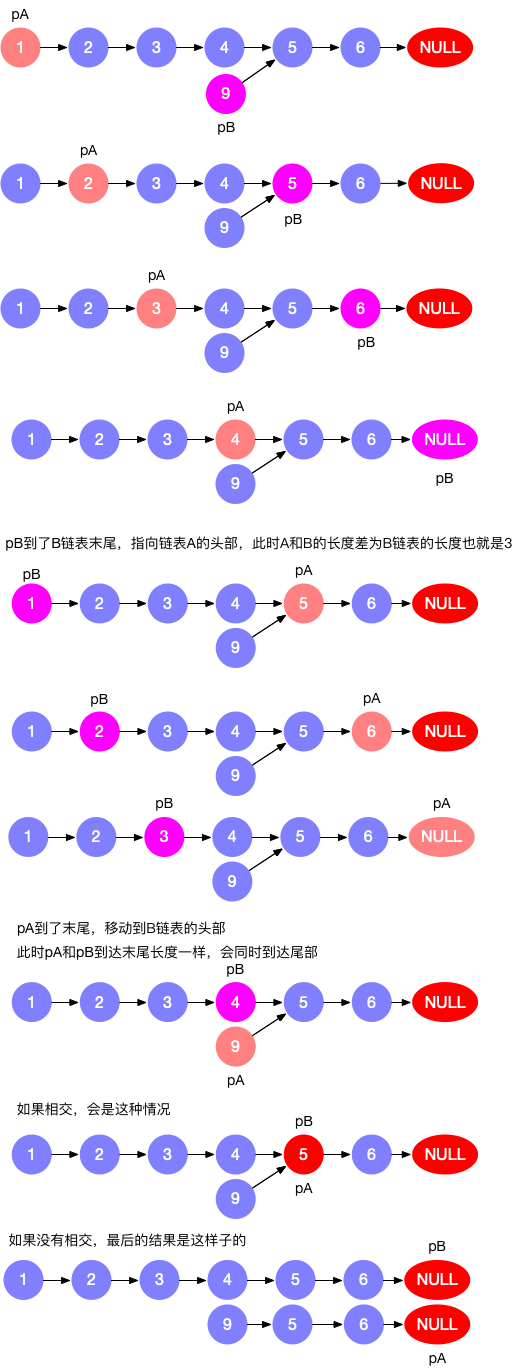
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode *pA = headA, *pB = headB;
while (pA != pB) {
pA = pA == nullptr ? headB : pA->next;
pB = pB == nullptr ? headA : pB->next;
}
return pA;
}
};
169. 多数元素

Approach 1: Brute Force
Intuition
We can exhaust the search space in quadratic time by checking whether each element is the majority element.
Algorithm
The brute force algorithm iterates over the array, and then iterates again for each number to count its occurrences. As soon as a number is found to have appeared more than any other can possibly have appeared, return it.
Complexity Analysis
Time complexity : O(n^2)
The brute force algorithm contains two nested for loops that each run for nn iterations, adding up to quadratic time complexity.
Space complexity : O(1)
The brute force solution does not allocate additional space proportional to the input size.
Solution 1 哈希表

Solution 2 排序
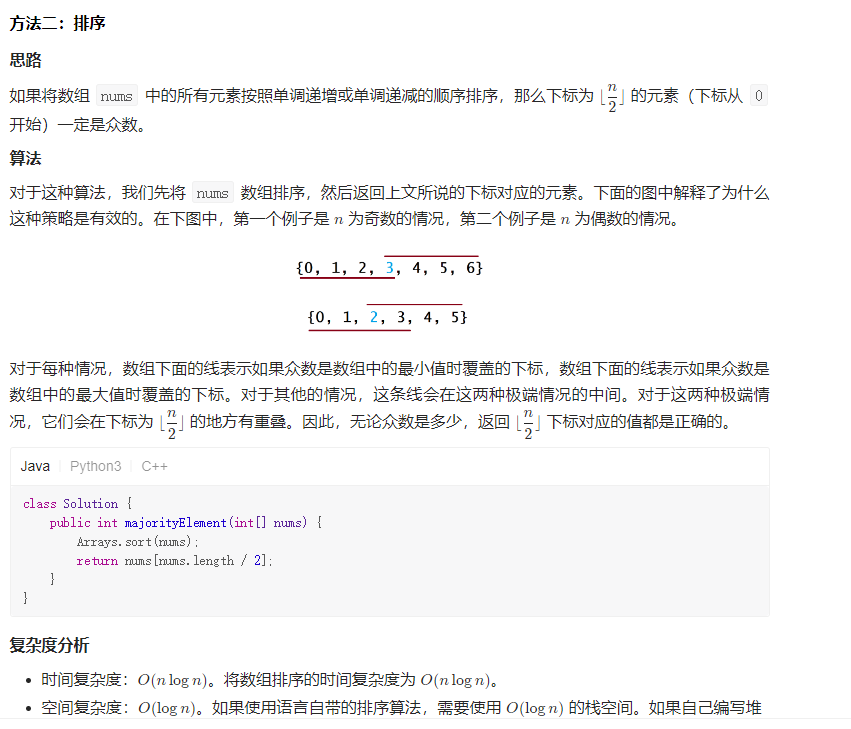
Solution 3 Boyer-Moore 投票法
172. 阶乘后的零
给定一个整数 n ,返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * … * 3 * 2 * 1
示例 1:
输入:n = 3
输出:0
解释:3! = 6 ,不含尾随 0
示例 2:
输入:n = 5
输出:1
解释:5! = 120 ,有一个尾随 0
示例 3:
输入:n = 0
输出:0
提示:
0 <= n <= 104

Solution1
首先题目的意思是末尾有几个0
比如6! = 【1* 2* 3* 4* 5* 6】
其中只有25末尾才有0,所以就可以抛去其他数据 专门看2 5 以及其倍数 毕竟 4 * 25末尾也是0
比如10! = 【2456810】
其中 4能拆成22 10能拆成25
所以10! = 【2*(22)5(23)(222)(2*5)】
一个2和一个5配对 就产生一个0 所以10!末尾2个0
转头一想 2肯定比5多 所以只数5的个数就行了
假若N=31 31里能凑10的5为[5, 2*5, 3*5, 4*5, 25, 6*5]
class Solution {
public:
int trailingZeroes(int n) {
int res=0;
for(int i=n;i>0;i/=5){
res+=i/5;
}
return res;
}
};
179. 最大数
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2]
输出:“210”
示例 2:
输入:nums = [3,30,34,5,9]
输出:“9534330”
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 109
Intuition
To construct the largest number, we want to ensure that the most significant digits are occupied by the largest digits.
Algorithm
First, we convert each integer to a string. Then, we sort the array of strings.
While it might be tempting to simply sort the numbers in descending order, this causes problems for sets of numbers with the same leading digit. For example, sorting the problem example in descending order would produce the number 95343039534303, while the correct answer can be achieved by transposing the 33 and the 3030. Therefore, for each pairwise comparison during the sort, we compare the numbers achieved by concatenating the pair in both orders. We can prove that this sorts into the proper order as follows:
Assume that (without loss of generality), for some pair of integers aa and bb, our comparator dictates that aa should precede bb in sorted order. This means that a\frown b > b\frown aa⌢b>b⌢a (where \frown⌢ represents concatenation). For the sort to produce an incorrect ordering, there must be some cc for which bb precedes cc and cc precedes aa. This is a contradiction because a\frown b > b\frown aa⌢b>b⌢a and b\frown c > c\frown bb⌢c>c⌢b implies a\frown c > c\frown aa⌢c>c⌢a. In other words, our custom comparator preserves transitivity, so the sort is correct.
Once the array is sorted, the most "signficant" number will be at the front. There is a minor edge case that comes up when the array consists of only zeroes, so if the most significant number is 00, we can simply return 00. Otherwise, we build a string out of the sorted array and return it.
Solution0 暴力
Solution1 排序
自定义一种排序方式 比较 s1 + s2 和 s2 + s1
class Solution {
public:
static bool cmp(int a,int b){
string sa = to_string(a);
string sb = to_string(b);
return sa+sb>sb+sa;
}
string largestNumber(vector<int>& nums) {
sort(nums.begin(),nums.end(),cmp);
string ret;
for(auto num:nums){
if(!(num==0&&ret[0]=='0')) ret+=to_string(num);
}
return ret;
}
};

187. 重复的DNA序列
DNA序列 由一系列核苷酸组成,缩写为 ‘A’, ‘C’, ‘G’ 和 ‘T’.。
例如,“ACGAATTCCG” 是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。
示例 1:
输入:s = “AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT”
输出:[“AAAAACCCCC”,“CCCCCAAAAA”]
示例 2:
输入:s = “AAAAAAAAAAAAA”
输出:[“AAAAAAAAAA”]
提示:
0 <= s.length <= 105
s[i]==‘A’、‘C’、‘G’ or ‘T’
Simple sliding window solution.
comments added for better explanation.
class Solution {
public:
vector<string> findRepeatedDnaSequences(string s) {
vector<string> ans;
map<string,int> mmap;
//storing the first 10 size substring(dna sequence)
//in temp
string temp=s.substr(0,10);
//adding first dna sequence to map
mmap[temp]++;
//now the sliding window.
for(int i=10;i<s.length();i++)
{
//remove first character from exsisting substring
temp=temp.substr(1);
//add the next character in substring.
temp=temp+s[i];
//add the new dna sequence to map.
mmap[temp]++;
//if the count of given sequence is greater than 2
//and it is not present in out ans vector push it in
//it
//we have done the find operation to keep the elements in answer vector
//unique.
//for example if aa...a sequence is present 4 times, it will adding 4 times
//in ans according to our sliding window logic. but we want it only one time.
//therefore we check in our vector if the given dna sequence is already present or not/
if(mmap[temp]>1 and find(ans.begin(),ans.end(),temp)==ans.end())
{
ans.push_back(temp);
}
}
return ans;
}
};
Solution1 哈希表
我们可以用一个哈希表统计 ss 所有长度为 1010 的子串的出现次数,返回所有出现次数超过 1010 的子串。
代码实现时,可以一边遍历子串一边记录答案,为了不重复记录答案,我们只统计当前出现次数为 22 的子串。
class Solution {
const int L = 10;
public:
vector<string> findRepeatedDnaSequences(string s) {
vector<string> ans;
unordered_map<string, int> cnt;
int n = s.length();
for (int i = 0; i <= n - L; ++i) {
string sub = s.substr(i, L);
if (++cnt[sub] == 2) {
ans.push_back(sub);
}
}
return ans;
}
};
Solution2 哈希表 滑动窗口 二进制

class Solution {
const int L = 10;
unordered_map<char, int> bin = {{'A', 0}, {'C', 1}, {'G', 2}, {'T', 3}};
public:
vector<string> findRepeatedDnaSequences(string s) {
vector<string> ans;
int n = s.length();
if (n <= L) {
return ans;
}
int x = 0;
for (int i = 0; i < L - 1; ++i) {
x = (x << 2) | bin[s[i]];
}
unordered_map<int, int> cnt;
for (int i = 0; i <= n - L; ++i) {
x = ((x << 2) | bin[s[i + L - 1]]) & ((1 << (L * 2)) - 1);
if (++cnt[x] == 2) {
ans.push_back(s.substr(i, L));
}
}
return ans;
}
};
189. 轮转数组
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105
// o(n) This solution is simply reversing the array and the reversing array from 0 to k-1 and then from k to n-1. Do a dry run by taking an example on copy and you will usndersand it.
// o(n) Using extra space approach we simply store the last k elemets in same order from n-k to n-1 in a temp vector and we then pushback the reaining elements in the temp vector from index 0 to n-k-1;
/ o(n*k) we roatate elements of the vector one by one for k times and achieve k roatations.
Solution1 使用额外的数组

Solution2 数组翻转
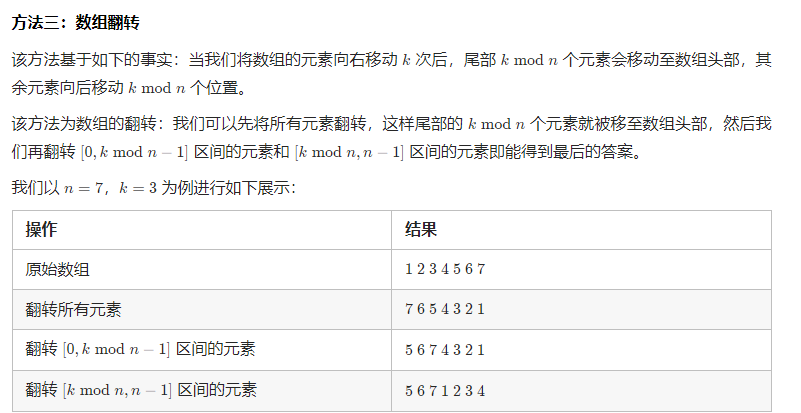
class Solution {
public:
void reverse(vector<int>& nums, int start, int end) {
while (start < end) {
swap(nums[start], nums[end]);
start += 1;
end -= 1;
}
}
void rotate(vector<int>& nums, int k) {
k %= nums.size();
reverse(nums, 0, nums.size() - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.size() - 1);
}
};
202. 快乐数
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
示例 2:
输入:n = 2
输出:false
提示:
1 <= n <= 231 - 1
1.hash-set
The hash-set solution is very straightforward. For every new data, we check whether it is already in the set. If no, we insert it into the set. If yes, we detect the loop. Only when the node in the loop is "1", the number is happy number.
2.hash-map
The idea is similar as hase-set. We check the node value to check whether it is in the loop.
The code is as follow. The time complexity usually is O(1) (the worst may be O(n) due to conflict)
3.Floyd's Cycle detection algorithm
Floyd's cycle detection algorithm is a pointer algorithm that uses only two pointers, which move through the sequence at different speeds. Obviously, if there is a loop, they will meet in the loop. It is also called the "tortoise and the hare algorithm"
4.Brent's Cycle detection algorithm
Brent's algorithm features a moving rabbit and a stationary, then teleporting, turtle. Both turtle and rabbit start at the top of the list. The rabbit takes one step per iteration. Every once in a while, we teleport the turtle to the rabbit's position, and let the rabbit continue moving. We start out waiting just 2 steps before teleportation, and we double that each time we move the turtle. If there is a loop, they will meet in the loop.
The code is as follows. The time complexity is O(λ + μ)*. However you're doing less stepping than with Floyd's (in fact the upper bound for steps is the number you would do with Floyd's algorithm). According to Brent's research, his algorithm is 24-36% faster on average for implicit linked list algorithms.(However, it cost same time as the Floyd's in the OJ ;) )
Solution1 快慢指针
//参考英文网站热评第一。这题可以用快慢指针的思想去做,有点类似于检测是否为环形链表那道题
//如果给定的数字最后会一直循环重复,那么快的指针(值)一定会追上慢的指针(值),也就是
//两者一定会相等。如果没有循环重复,那么最后快慢指针也会相等,且都等于1。
class Solution {
public boolean isHappy(int n) {
int fast=n;
int slow=n;
do{
slow=squareSum(slow);
fast=squareSum(fast);
fast=squareSum(fast);
}while(slow!=fast);
if(fast==1)
return true;
else return false;
}
private int squareSum(int m){
int squaresum=0;
while(m!=0){
squaresum+=(m%10)*(m%10);
m/=10;
}
return squaresum;
}
}
Solution2 暴力
class Solution {
public:
bool isHappy(int n) {
int ans=0;
for(int i = 0 ; i< 100;i++)
{
while(n>0)
{
ans += (n%10)*(n%10);
n = n /10;
}
n = ans;
if(n==1)
return true;
}
return false;
}
};
203. 移除链表元素
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
示例 1:
输入:head = [1,2,6,3,4,5,6], val = 6
输出:[1,2,3,4,5]
示例 2:
输入:head = [], val = 1
输出:[]
示例 3:
输入:head = [7,7,7,7], val = 7
输出:[]
提示:
列表中的节点数目在范围 [0, 104] 内
1 <= Node.val <= 50
0 <= val <= 50
✔️ Solution - I (Iterative using Dummy node)
A simple solution to delete the nodes having value T is to traverse over the linked list and just remove the next pointers to the node having value as T. Now, usually in deletion problem of linked list, there can be multiple cases where node to be deleted is either a head node or other node in rest of list. We usually make use of a dummy node at the start or sentinel node to avoid handling multiple edge cases and write a clean uniform solution.
So, the algorithm we are using can be summarised as -
Initialize a dummy/sentinel node having its next pointer pointing to the head of linked list and another node pointer prev pointing to this dummy node.
Start iterating over head of linked list
If current node's value is not equal to T, we can just move to next node without deleting current node. In this case,
We first update prev pointer and point it to current head
Then move head to next node.
Otherwise, if head -> val == T, we know that this node needs to be deleted. In this case,
We can just update the next pointer of previous node to the next pointer of current node. This will basically remove the current node from list.
Then, we update head to its next node just as in previous case.
Finally, ignore the dummy node created at start and return its next node.
Solution1 迭代
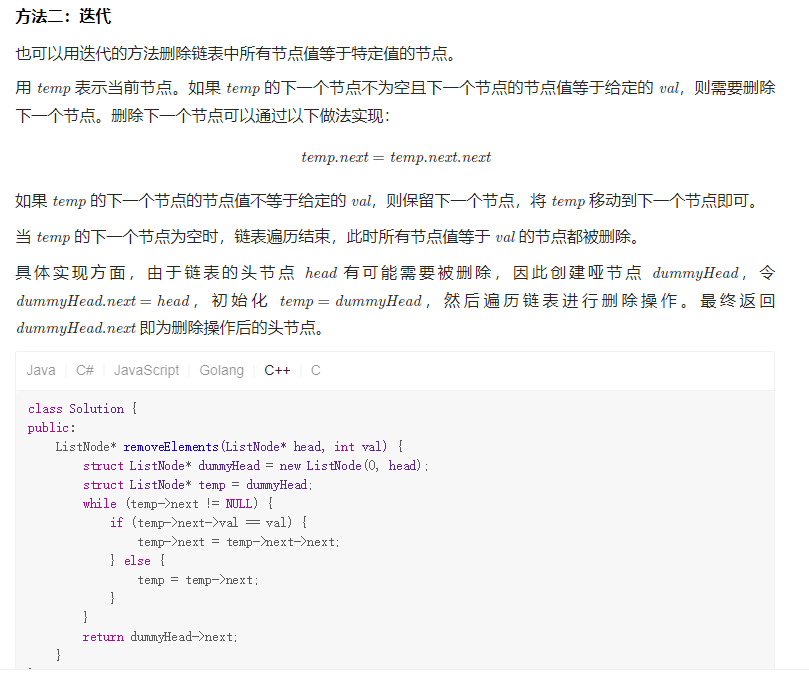
Solution2 递归
ListNode *removeElements(ListNode *head, int val)
{
if (!head)
return head;
head->next = removeElements(head->next, val);
return head->val == val ? head->next : head;
}
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是链表的长度。需要遍历链表一次。
空间复杂度:O(1)O(1)。
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104
This problem is well known and quite often can be found in various text books.
You can take a couple of approaches to actually solve it:
O(N lg K) running time + O(K) memory
Other possibility is to use a min oriented priority queue that will store the K-th largest values. The algorithm iterates over the whole input and maintains the size of priority queue.
O(N) best case / O(N^2) worst case running time + O(1) memory
The smart approach for this problem is to use the selection algorithm (based on the partion method - the same one as used in quicksort).
O(N) guaranteed running time + O(1) space
So how can we improve the above solution and make it O(N) guaranteed? The answer is quite simple, we can randomize the input, so that even when the worst case input would be provided the algorithm wouldn't be affected. So all what it is needed to be done is to shuffle the input.
Solution1 堆排序
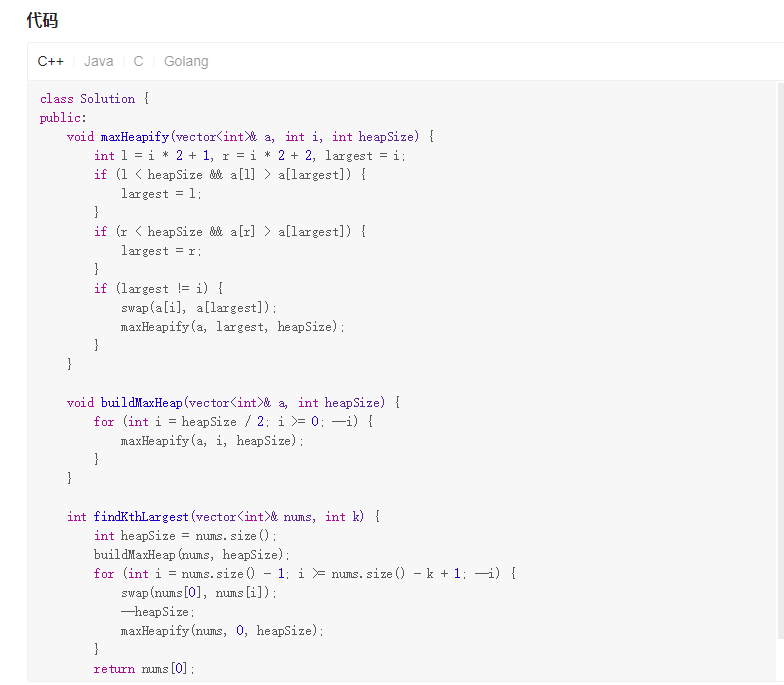
复杂度分析
时间复杂度:O(n \log n)O(nlogn),建堆的时间代价是 O(n)O(n),删除的总代价是 O(k \log n)O(klogn),因为 k < nk<n,故渐进时间复杂为 O(n + k \log n) = O(n \log n)O(n+klogn)=O(nlogn)。
空间复杂度:O(\log n)O(logn),即递归使用栈空间的空间代价。

217. 存在重复元素
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1]
输出:true
示例 2:
输入:nums = [1,2,3,4]
输出:false
示例 3:
输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true
提示:
1 <= nums.length <= 105
-109 <= nums[i] <= 109
This problem seems trivial, so lets try different approaches to solve it:
Starting from worst time complexity to the best one:
Time complexity: O(N^2), memory: O(1)
The naive approach would be to run a iteration for each element and see whether a duplicate value can be found: this results in O(N^2) time complexity.
Time complexity: O(N lg N), memory: O(1) - not counting the memory used by sort
Since it is trivial task to find duplicates in sorted array, we can sort it as the first step of the algorithm and then search for consecutive duplicates.
Time complexity: O(N), memory: O(N)
Finally we can used a well known data structure hash table that will help us to identify whether an element has been previously encountered in the array.
This is trivial but quite nice example of space-time tradeoff.
Solution1 排序
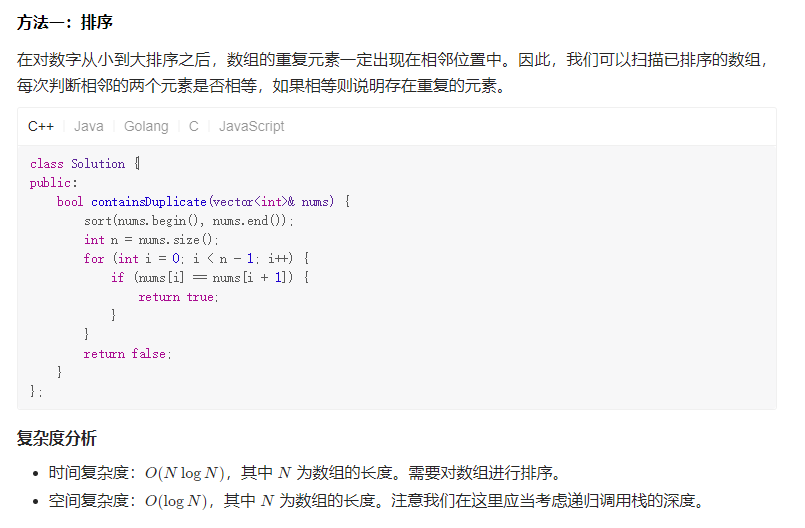
Solution2
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
[“MyStack”, “push”, “push”, “top”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
提示:
1 <= x <= 9
最多调用100 次 push、pop、top 和 empty
每次调用 pop 和 top 都保证栈不为空
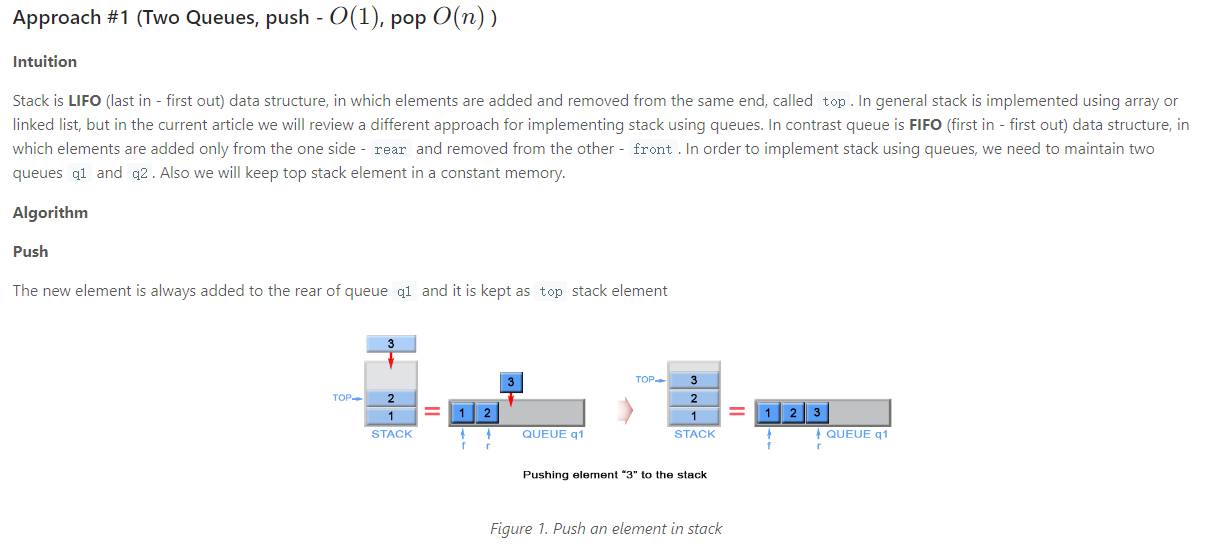
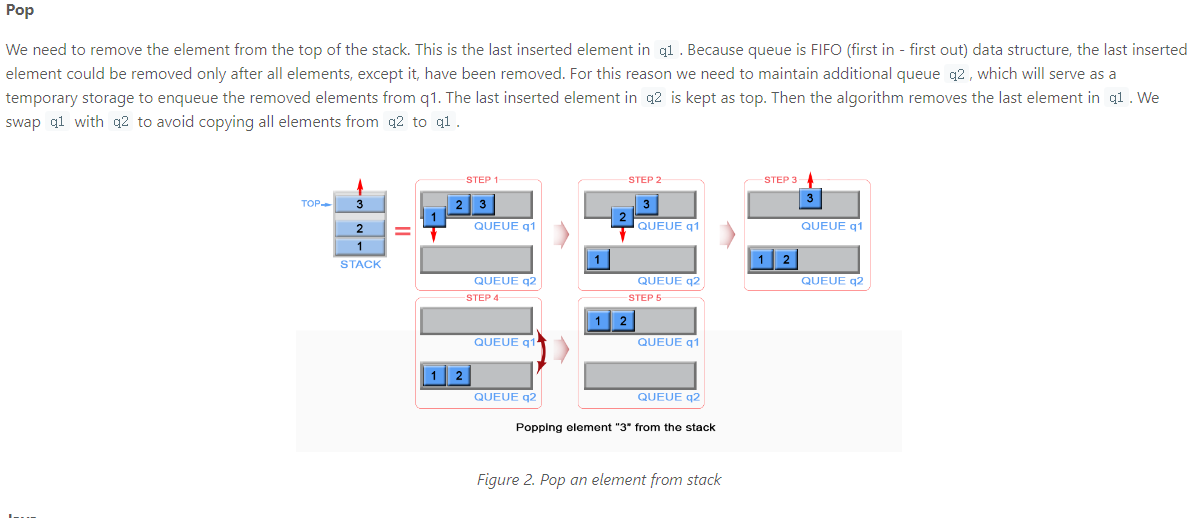
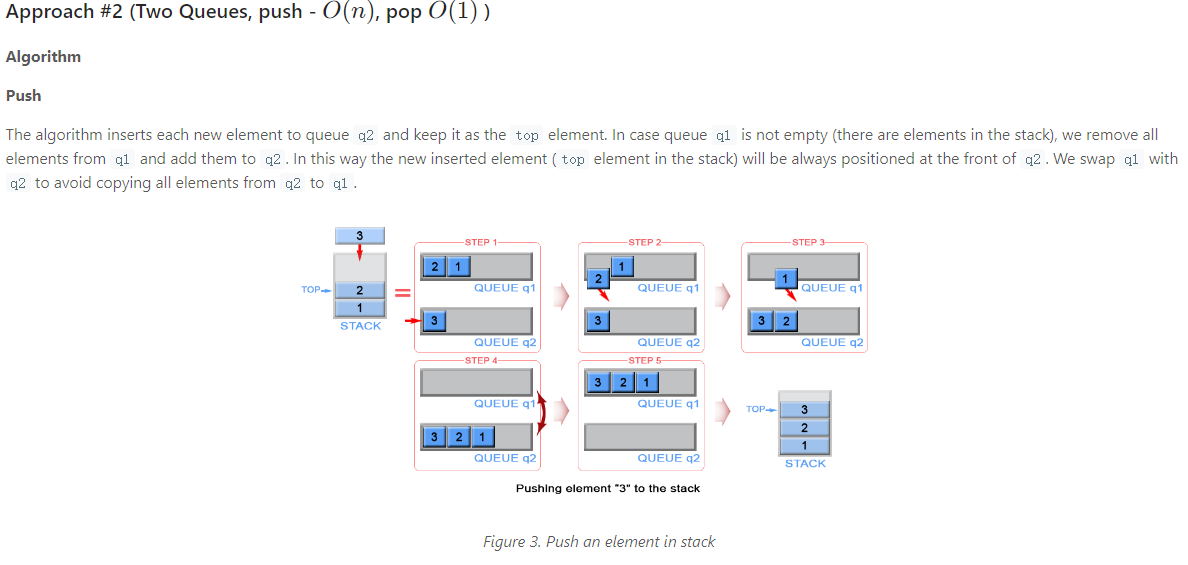
Solution1 两个队列

class MyStack {
public:
queue<int> queue1;
queue<int> queue2;
/** Initialize your data structure here. */
MyStack() {
}
/** Push element x onto stack. */
void push(int x) {
queue2.push(x);
while (!queue1.empty()) {
queue2.push(queue1.front());
queue1.pop();
}
swap(queue1, queue2);
}
/** Removes the element on top of the stack and returns that element. */
int pop() {
int r = queue1.front();
queue1.pop();
return r;
}
/** Get the top element. */
int top() {
int r = queue1.front();
return r;
}
/** Returns whether the stack is empty. */
bool empty() {
return queue1.empty();
}
};
Solution2 单个队列

227. 基本计算器 II
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
输入:s = “3+2*2”
输出:7
示例 2:
输入:s = " 3/2 "
输出:1
示例 3:
输入:s = " 3+5 / 2 "
输出:5
提示:
1 <= s.length <= 3 * 105
s 由整数和算符 (‘+’, ‘-’, ‘*’, ‘/’) 组成,中间由一些空格隔开
s 表示一个 有效表达式
表达式中的所有整数都是非负整数,且在范围 [0, 231 - 1] 内
题目数据保证答案是一个 32-bit 整数


Solution1 栈
方法一:栈
思路
由于乘除优先于加减计算,因此不妨考虑先进行所有乘除运算,并将这些乘除运算后的整数值放回原表达式的相应位置,则随后整个表达式的值,就等于一系列整数加减后的值。
基于此,我们可以用一个栈,保存这些(进行乘除运算后的)整数的值。对于加减号后的数字,将其直接压入栈中;对于乘除号后的数字,可以直接与栈顶元素计算,并替换栈顶元素为计算后的结果。
具体来说,遍历字符串 ss,并用变量 \textit{preSign}preSign 记录每个数字之前的运算符,对于第一个数字,其之前的运算符视为加号。每次遍历到数字末尾时,根据 \textit{preSign}preSign 来决定计算方式:
加号:将数字压入栈;
减号:将数字的相反数压入栈;
乘除号:计算数字与栈顶元素,并将栈顶元素替换为计算结果。
代码实现中,若读到一个运算符,或者遍历到字符串末尾,即认为是遍历到了数字末尾。处理完该数字后,更新 \textit{preSign}preSign 为当前遍历的字符。
遍历完字符串 ss 后,将栈中元素累加,即为该字符串表达式的值。
class Solution {
public:
int calculate(string s) {
vector<int> stk;
char preSign = '+';
int num = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (isdigit(s[i])) {
num = num * 10 + int(s[i] - '0');
}
if (!isdigit(s[i]) && s[i] != ' ' || i == n - 1) {
switch (preSign) {
case '+':
stk.push_back(num);
break;
case '-':
stk.push_back(-num);
break;
case '*':
stk.back() *= num;
break;
default:
stk.back() /= num;
}
preSign = s[i];
num = 0;
}
}
return accumulate(stk.begin(), stk.end(), 0);
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 为字符串 ss 的长度。需要遍历字符串 ss 一次,计算表达式的值。
空间复杂度:O(n)O(n),其中 nn 为字符串 ss 的长度。空间复杂度主要取决于栈的空间,栈的元素个数不超过 nn。
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
示例 1:
输入:
[“MyQueue”, “push”, “push”, “peek”, “pop”, “empty”]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 1, 1, false]
解释:
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

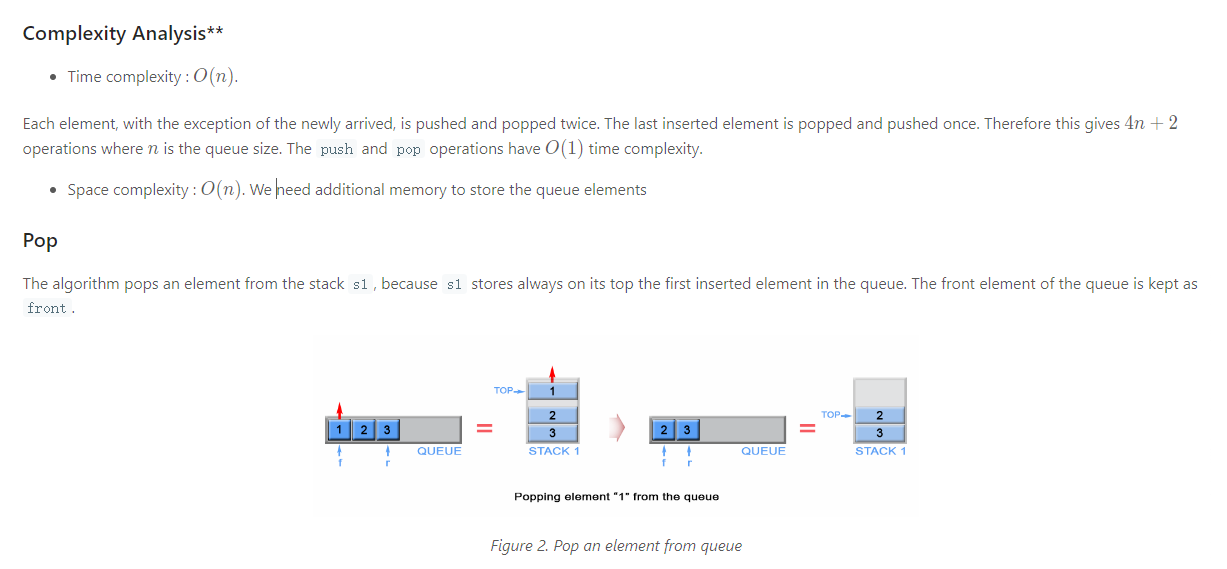
Solution1
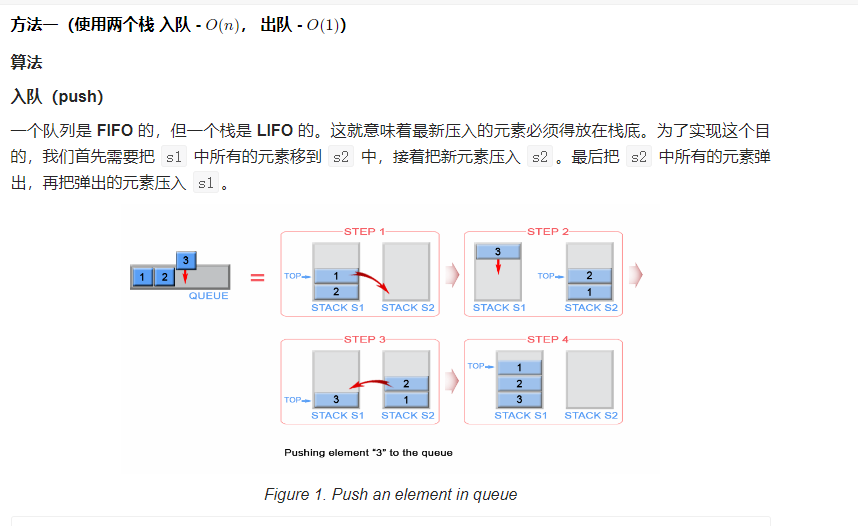
思路
将一个栈当作输入栈,用于压入 \texttt{push}push 传入的数据;另一个栈当作输出栈,用于 \texttt{pop}pop 和 \texttt{peek}peek 操作。
每次 \texttt{pop}pop 或 \texttt{peek}peek 时,若输出栈为空则将输入栈的全部数据依次弹出并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
class MyQueue {
private:
stack<int> inStack, outStack;
void in2out() {
while (!inStack.empty()) {
outStack.push(inStack.top());
inStack.pop();
}
}
public:
MyQueue() {}
void push(int x) {
inStack.push(x);
}
int pop() {
if (outStack.empty()) {
in2out();
}
int x = outStack.top();
outStack.pop();
return x;
}
int peek() {
if (outStack.empty()) {
in2out();
}
return outStack.top();
}
bool empty() {
return inStack.empty() && outStack.empty();
}
};

234. 回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
示例 1:
输入:head = [1,2,2,1]
输出:true
示例 2:
输入:head = [1,2]
输出:false
提示:
链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9
进阶:你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
Functions used below are HEART n SOUL of linkedlist questions. Usually, any LinkedList question can be broken down to these functions:-
Reverse ===> Used for space optimization
Find Mid ===> Slow-Fast Pointer
Iteration : normal iter, recursive iter, adjacent node 2-vars, slow-fast
Insert : start , mid, last
delete : start, mid, last
THIS QUESTION:
find Mid of linkedlist --------> do see cases of even/odd length on paper
reverse second half from mid pointer ----> see how prev gets changed
Now compare first and second half Easy huh! 😜
EdgeCase:
linkedlist size =0,1
Solution0 将链表复制到数组
class Solution {
public:
bool isPalindrome(ListNode* head) {
vector<int> vals;
while (head != nullptr) {
vals.emplace_back(head->val);
head = head->next;
}
for (int i = 0, j = (int)vals.size() - 1; i < j; ++i, --j) {
if (vals[i] != vals[j]) {
return false;
}
}
return true;
}
};
Solution1 中点开始比较
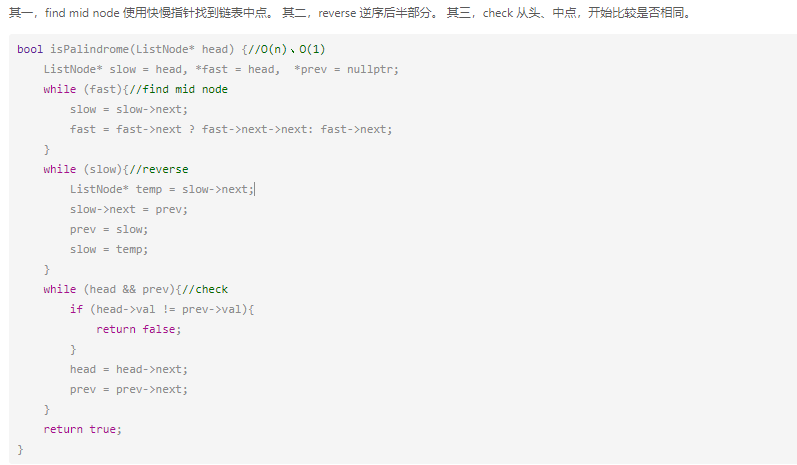
237. 删除链表中的节点
有一个单链表的 head,我们想删除它其中的一个节点 node。
给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。
链表的所有值都是 唯一的,并且保证给定的节点 node 不是链表中的最后一个节点。
删除给定的节点。注意,删除节点并不是指从内存中删除它。这里的意思是:
给定节点的值不应该存在于链表中。
链表中的节点数应该减少 1。
node 前面的所有值顺序相同。
node 后面的所有值顺序相同。
自定义测试:
对于输入,你应该提供整个链表 head 和要给出的节点 node。node 不应该是链表的最后一个节点,而应该是链表中的一个实际节点。
我们将构建链表,并将节点传递给你的函数。
输出将是调用你函数后的整个链表。
示例 1:
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:指定链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9
示例 2:
输入:head = [4,5,1,9], node = 1
输出:[4,5,9]
解释:指定链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9
提示:
链表中节点的数目范围是 [2, 1000]
-1000 <= Node.val <= 1000
链表中每个节点的值都是 唯一 的
需要删除的节点 node 是 链表中的节点 ,且 不是末尾节点
class Solution {
public void deleteNode(ListNode node) {
node.val=node.next.val;
node.next=node.next.next;
}
}
So, this is our code.
We don't have the access to the previous node of the to be deleted node.
But we have the access to the next node, which makes deletion of next node possible.
So, we copy the value of the next node to this node and delete the next node (i.e connecting our current node to the next node's next)
Hopefully you understood, Thank you 😀
Solution1
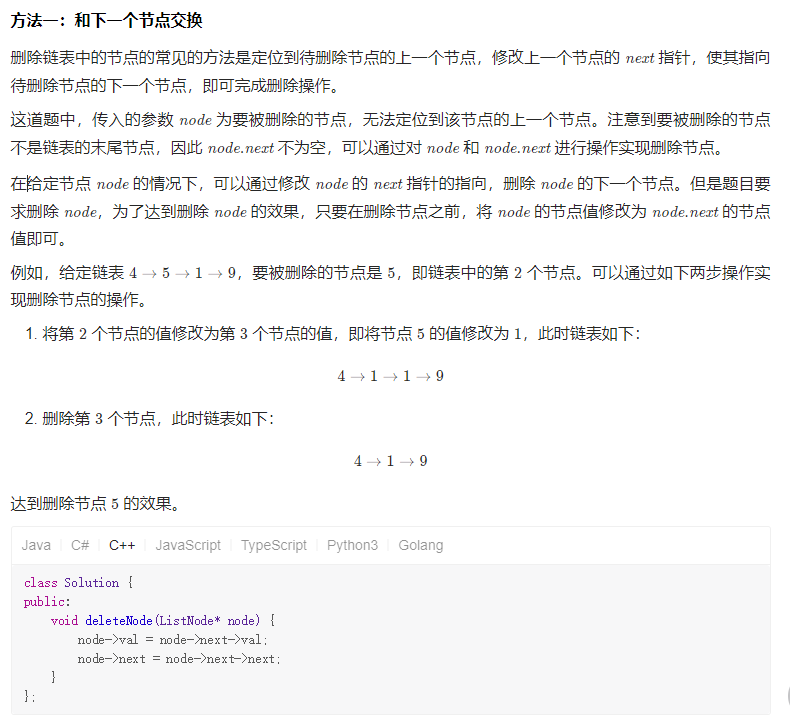
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
✔️ Solution - I (Calculate product & divide by self)
We can simply calculate product of the whole array and for each element in nums, divide the product by nums[i]. This effectively leaves us with product of whole array except self at each index. We need to take care of zeros that may occur in the array -
1. If there are more than one 0s in nums, the result is an array consisting of all 0.
2. If there is a single 0 in nums, then the result is an array consisting of all 0 except at the index where there was 0 in nums, which will contain product of rest of array.
3. If there's no 0 in nums, then the result is an array ans where ans[i] = prod / nums[i] (prod = product of all elements in nums).
Solution1 累乘列表

class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
// L 和 R 分别表示左右两侧的乘积列表
vector<int> L(length, 0), R(length, 0);
vector<int> answer(length);
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
};
Solution2 空间复杂度为O(1)的方法

class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
vector<int> answer(length);
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
}
};
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例 1:
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
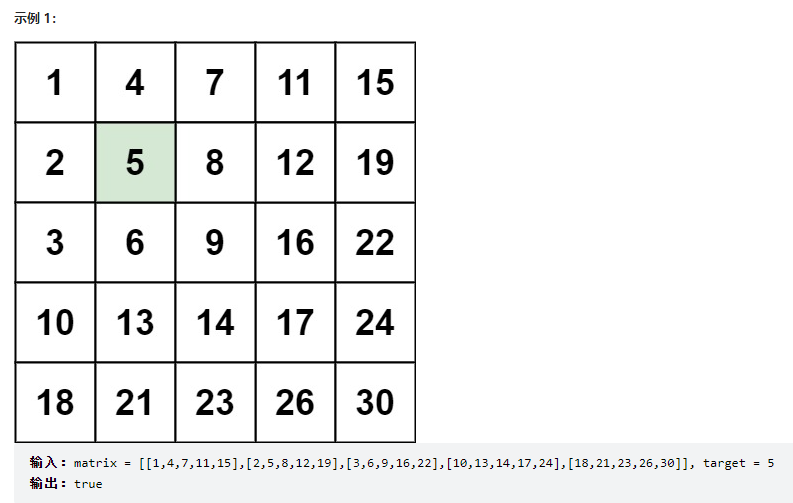
提示:
m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109
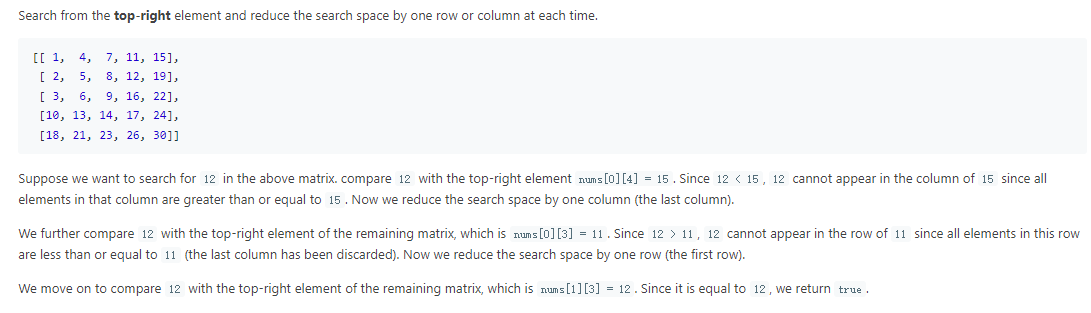
Solution0 暴力
Solution1 从右上角看是一颗二叉搜索树
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
if(matrix.size() == 0) {
return false;
}
int i = 0;
int j = matrix[0].size()-1;
while(i < matrix.size() && j >= 0) {
if(matrix[i][j] == target) {
return true;
}
if(matrix[i][j] < target) {
++ i;
}
else {
-- j;
}
}
return false;
}
};
242. 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1:
输入: s = “anagram”, t = “nagaram”
输出: true
示例 2:
输入: s = “rat”, t = “car”
输出: false
提示:
1 <= s.length, t.length <= 5 * 104
s 和 t 仅包含小写字母
Hash Table
This idea uses a hash table to record the times of appearances of each letter in the two strings s and t. For each letter in s, it increases the counter by 1 while for each letter in t, it decreases the counter by 1. Finally, all the counters will be 0 if they two are anagrams of each other.
The first implementation uses the built-in unordered_map and takes 36 ms.
class Solution {
public:
bool isAnagram(string s, string t) {
if (s.length() != t.length()) return false;
int n = s.length();
unordered_map<char, int> counts;
for (int i = 0; i < n; i++) {
counts[s[i]]++;
counts[t[i]]--;
}
for (auto count : counts)
if (count.second) return false;
return true;
}
};
Since the problem statement says that "the string contains only lowercase alphabets", we can simply use an array to simulate the unordered_map and speed up the code. The following implementation takes 12 ms.
class Solution {
public:
bool isAnagram(string s, string t) {
if (s.length() != t.length()) return false;
int n = s.length();
int counts[26] = {0};
for (int i = 0; i < n; i++) {
counts[s[i] - 'a']++;
counts[t[i] - 'a']--;
}
for (int i = 0; i < 26; i++)
if (counts[i]) return false;
return true;
}
};
Sorting
For two anagrams, once they are sorted in a fixed order, they will become the same. This code is much shorter (this idea can be done in just 1 line using Python as here). However, it takes much longer time --- 76 ms in C++.
class Solution {
public:
bool isAnagram(string s, string t) {
sort(s.begin(), s.end());
sort(t.begin(), t.end());
return s == t;
}
};
C++ 三种方法:
Solution1 1.直接用sort函数
class Solution {
public:
bool isAnagram(string s, string t) {
sort(s.begin(),s.end());
sort(t.begin(),t.end());
if(s==t)
return true;
else
return false;
}
};
Solution2 2.map计数
class Solution {
public:
bool isAnagram(string s, string t) {
unordered_map<char,int> map;
if (s.size() != t.size())
return false;
for(int i=0;i<s.size();i++){
++map[s[i]];
–map[t[i]];
}
for(unordered_map<char,int>::iterator it=map.begin();it!=map.end();it++){
if(it->second!=0)
return false;
}
return true;
}
};
Solution3 3.效率最高
class Solution {
public:
bool isAnagram(string s, string t) {
int num[26]={0};
if(s.length()!=t.length())
return false;
for(int i=0;s[i]!=‘\0’;i++){
num[s[i]-‘a’]++;
num[t[i]-‘a’]–;
}
for(int i=0;i<26;i++)
if(num[i]!=0)
return false;
return true;
}
};
258. 各位相加
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。返回这个结果。
示例 1:
输入: num = 38
输出: 2
解释: 各位相加的过程为:
38 --> 3 + 8 --> 11
11 --> 1 + 1 --> 2
由于 2 是一位数,所以返回 2。
示例 1:
输入: num = 0
输出: 0
提示:
0 <= num <= 231 - 1
进阶:你可以不使用循环或者递归,在 O(1) 时间复杂度内解决这个问题吗?
Math's Explained :-
Any number where it's digits add to 9 is always divisible by 9. (18, 27, 36, 45, 54, 63, 72, 81, 90, etc.) Therefore the 'digital root' for any number divisible by 9 is always 9. You can see this even in larger numbers like 99 because 9 + 9 = 18, and then 1 + 8 = 9 still, so the root always becomes 9 for any numbers divisible by 9.
Additionally, 0 always has a digital root of 0 obviously.
The only other cases you need to worry about to find the digital root are when it isn't 0 or 9.
So for any number that isn't 0 and isn't divisible by 9, the root will always n % 9 for a given number n. (AKA the difference between given number n and the nearest number that is divisible by 9, since numbers divisible by 9 always have a digital root of 9).
For examples: 100 % 9 = 1 (one greater than 99, which is divisible by 9).
101 % 9 = 2
102 % 9 = 3 and so on.
This explanation/algorithm skips the whole "add digits until there is only 1 remaining", so the description of this problem seems pretty misleading to me since it makes you think the solution will be something unrelated to the optimal one. I guess the point of Leetcode is to learn all of these tricks though.
Solution1 : 找规律
除了传统的单纯循环,还可以找规律。假如一个三位数’abc’,其值大小为s1 = 100 * a + 10 * b + 1 * c,经过一次各位相加后,变为s2 = a + b + c,减小的差值为(s1 -s2) = 99 * a + 9 * b,差值可以被9整除,每一个循环都这样,缩小了9的倍数。当num小于9,即只有一位时,直接返回num,大于9时,如果能被9整除,则返回9(因为不可能返回0也不可能返回两位数及以上的值),如果不能被整除,就返回被9除的余数。
class Solution:
def addDigits(self, num: int) -> int:
if num > 9:
num = num % 9
if num == 0:
return 9
return num
Solution2 :循环
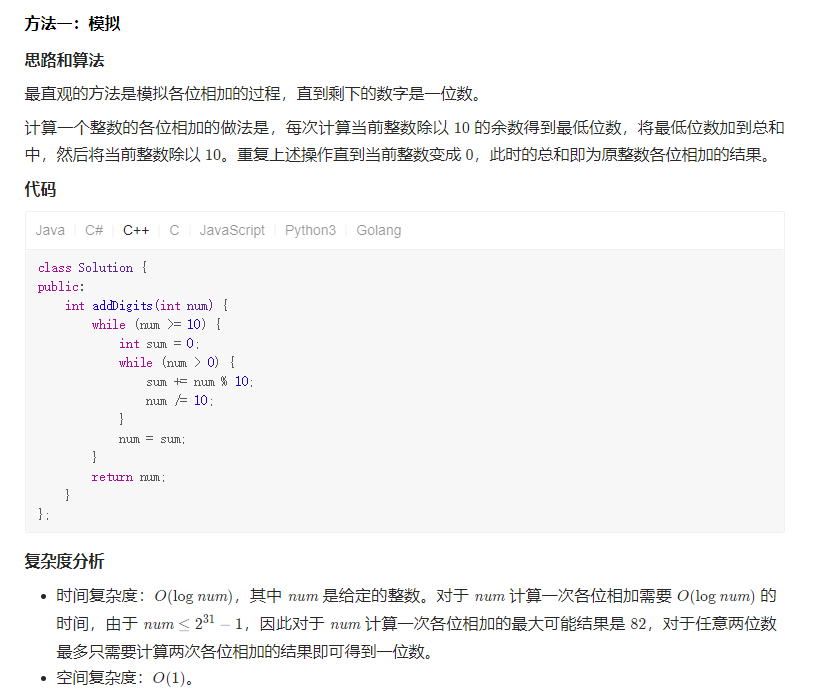
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
Solution
This question comes under a broad category of "Array Transformation". This category is the meat of tech interviews. Mostly because arrays are such a simple and easy to use data structure. Traversal or representation doesn't require any boilerplate code and most of your code will look like the Pseudocode itself.
The 2 requirements of the question are:
Move all the 0's to the end of array.
All the non-zero elements must retain their original order.
It's good to realize here that both the requirements are mutually exclusive, i.e., you can solve the individual sub-problems and then combine them for the final solution.
Approach #1 (Space Sub-Optimal) [Accepted]
C++
void moveZeroes(vector<int>& nums) {
int n = nums.size();
// Count the zeroes
int numZeroes = 0;
for (int i = 0; i < n; i++) {
numZeroes += (nums[i] == 0);
}
// Make all the non-zero elements retain their original order.
vector<int> ans;
for (int i = 0; i < n; i++) {
if (nums[i] != 0) {
ans.push_back(nums[i]);
}
}
// Move all zeroes to the end
while (numZeroes--) {
ans.push_back(0);
}
// Combine the result
for (int i = 0; i < n; i++) {
nums[i] = ans[i];
}
}
Complexity Analysis
Space Complexity : O(n)O(n). Since we are creating the "ans" array to store results.
Time Complexity: O(n)O(n). However, the total number of operations are sub-optimal. We can achieve the same result in less number of operations.
If asked in an interview, the above solution would be a good start. You can explain the interviewer(not code) the above and build your base for the next Optimal Solution.
Approach #2 (Space Optimal, Operation Sub-Optimal) [Accepted]
This approach works the same way as above, i.e. , first fulfills one requirement and then another. The catch? It does it in a clever way. The above problem can also be stated in alternate way, " Bring all the non 0 elements to the front of array keeping their relative order same".
This is a 2 pointer approach. The fast pointer which is denoted by variable "cur" does the job of processing new elements. If the newly found element is not a 0, we record it just after the last found non-0 element. The position of last found non-0 element is denoted by the slow pointer "lastNonZeroFoundAt" variable. As we keep finding new non-0 elements, we just overwrite them at the "lastNonZeroFoundAt + 1" 'th index. This overwrite will not result in any loss of data because we already processed what was there(if it were non-0,it already is now written at it's corresponding index,or if it were 0 it will be handled later in time).
After the "cur" index reaches the end of array, we now know that all the non-0 elements have been moved to beginning of array in their original order. Now comes the time to fulfil other requirement, "Move all 0's to the end". We now simply need to fill all the indexes after the "lastNonZeroFoundAt" index with 0.
C++
void moveZeroes(vector<int>& nums) {
int lastNonZeroFoundAt = 0;
// If the current element is not 0, then we need to
// append it just in front of last non 0 element we found.
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != 0) {
nums[lastNonZeroFoundAt++] = nums[i];
}
}
// After we have finished processing new elements,
// all the non-zero elements are already at beginning of array.
// We just need to fill remaining array with 0's.
for (int i = lastNonZeroFoundAt; i < nums.size(); i++) {
nums[i] = 0;
}
}
Complexity Analysis
Space Complexity : O(1)O(1). Only constant space is used.
Time Complexity: O(n)O(n). However, the total number of operations are still sub-optimal. The total operations (array writes) that code does is nn (Total number of elements).
Approach #3 (Optimal) [Accepted]
The total number of operations of the previous approach is sub-optimal. For example, the array which has all (except last) leading zeroes: [0, 0, 0, ..., 0, 1].How many write operations to the array? For the previous approach, it writes 0's n-1n−1 times, which is not necessary. We could have instead written just once. How? ..... By only fixing the non-0 element,i.e., 1.
The optimal approach is again a subtle extension of above solution. A simple realization is if the current element is non-0, its' correct position can at best be it's current position or a position earlier. If it's the latter one, the current position will be eventually occupied by a non-0 ,or a 0, which lies at a index greater than 'cur' index. We fill the current position by 0 right away,so that unlike the previous solution, we don't need to come back here in next iteration.
In other words, the code will maintain the following invariant:
All elements before the slow pointer (lastNonZeroFoundAt) are non-zeroes.
All elements between the current and slow pointer are zeroes.
Therefore, when we encounter a non-zero element, we need to swap elements pointed by current and slow pointer, then advance both pointers. If it's zero element, we just advance current pointer.
With this invariant in-place, it's easy to see that the algorithm will work.
C++
void moveZeroes(vector<int>& nums) {
for (int lastNonZeroFoundAt = 0, cur = 0; cur < nums.size(); cur++) {
if (nums[cur] != 0) {
swap(nums[lastNonZeroFoundAt++], nums[cur]);
}
}
}
Complexity Analysis
Space Complexity : O(1)O(1). Only constant space is used.
Time Complexity: O(n)O(n). However, the total number of operations are optimal. The total operations (array writes) that code does is Number of non-0 elements.This gives us a much better best-case (when most of the elements are 0) complexity than last solution. However, the worst-case (when all elements are non-0) complexity for both the algorithms is same.
Solution1
void moveZeroes(int* nums, int numsSize) {
int i = 0,j = 0;
for(i = 0 ; i < numsSize; i++)
{
if(nums[i] != 0)
{
nums[j++] = nums[i];
}
}
while(j < numsSize)
{
nums[j++] = 0;
}
}
292. Nim 游戏
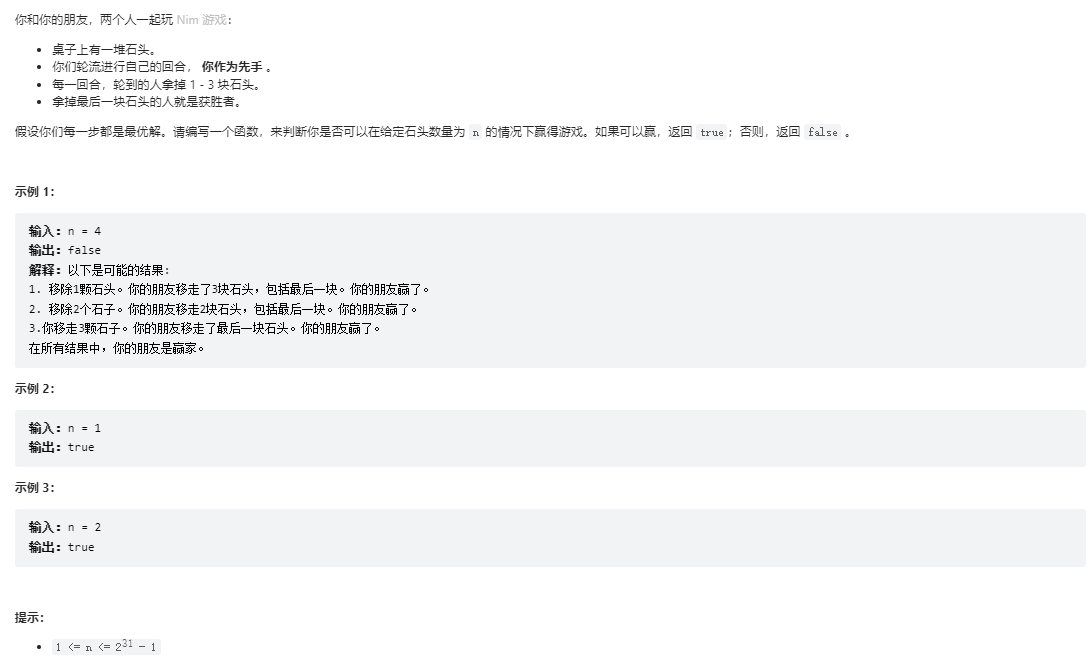
Solution
You can always win a Nim game if the number of stones nn in the pile is not divisible by 44.
Reasoning
Let us think of the small cases. It is clear that if there are only one, two, or three stones in the pile, and it is your turn, you can win the game by taking all of them. Like the problem description says, if there are exactly four stones in the pile, you will lose. Because no matter how many you take, you will leave some stones behind for your opponent to take and win the game. So in order to win, you have to ensure that you never reach the situation where there are exactly four stones on the pile on your turn.
Similarly, if there are five, six, or seven stones you can win by taking just enough to leave four stones for your opponent so that they lose. But if there are eight stones on the pile, you will inevitably lose, because regardless whether you pick one, two or three stones from the pile, your opponent can pick three, two or one stone to ensure that, again, four stones will be left to you on your turn.
It is obvious that the same pattern repeats itself for n=4,8,12,16,\dotsn=4,8,12,16,…, basically all multiples of 44.
Complexity Analysis
Time complexity: O(1)O(1)
Only one check is performed.
Space complexity: O(1)O(1)
No additional space is used, so space complexity is also O(1)O(1).
Solution1 数学推理
326.3的幂


Solution1 试除法
Solution2 约数法
328. 奇偶链表
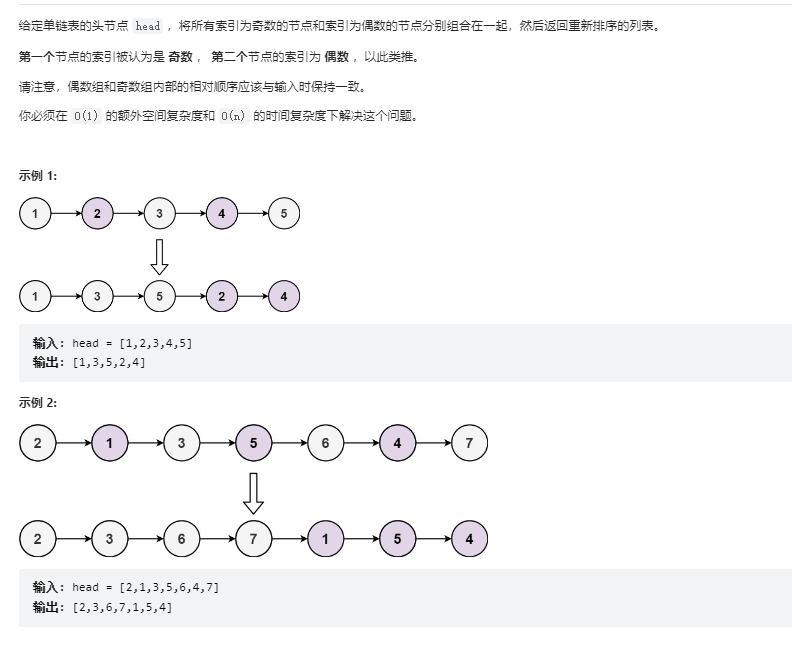
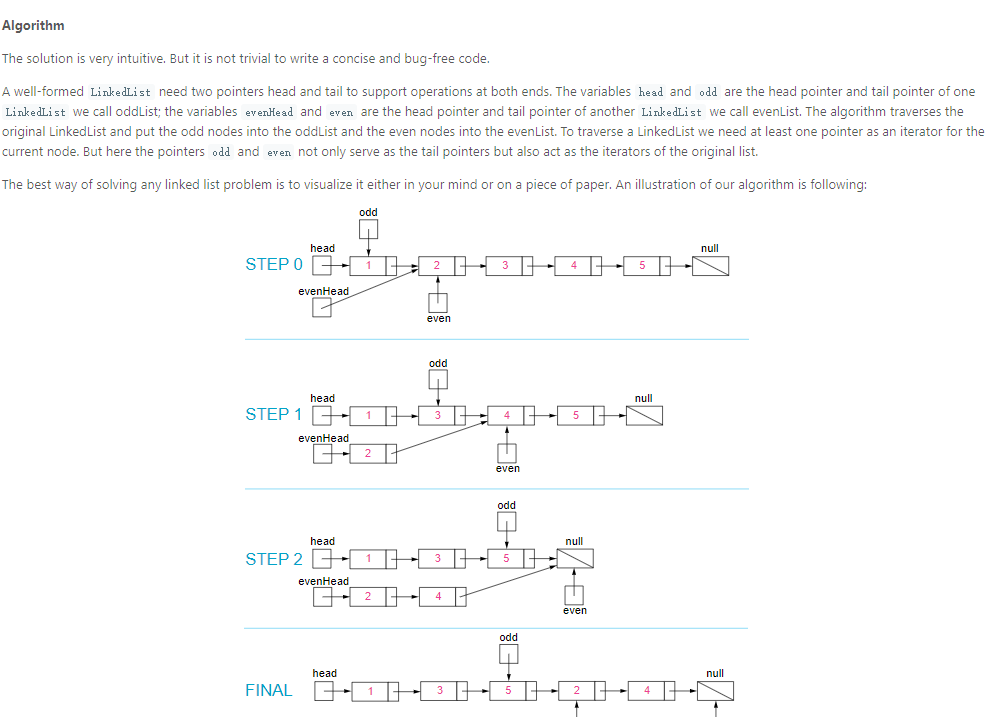
Solution1 双链法
结点1作为奇数链的头 结点2作为偶数链的头
从第3个点开始遍历,依次轮流附在奇、偶链的后面
遍历完后,奇数链的尾连向偶链的头,偶链的尾为空, 返回奇数链的头
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
if (head == nullptr) {
return head;
}
ListNode* evenHead = head->next;
ListNode* odd = head;
ListNode* even = evenHead;
while (even != nullptr && even->next != nullptr) {
odd->next = even->next;
odd = odd->next;
even->next = odd->next;
even = even->next;
}
odd->next = evenHead;
return head;
}
};
复杂度分析
时间复杂度:O(n)O(n),其中 nn 是链表的节点数。需要遍历链表中的每个节点,并更新指针。
空间复杂度:O(1)O(1)。只需要维护有限的指针。
334. 递增的三元子序列
给你一个整数数组 nums ,判断这个数组中是否存在长度为 3 的递增子序列。
如果存在这样的三元组下标 (i, j, k) 且满足 i < j < k ,使得 nums[i] < nums[j] < nums[k] ,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [1,2,3,4,5]
输出:true
解释:任何 i < j < k 的三元组都满足题意
示例 2:
输入:nums = [5,4,3,2,1]
输出:false
解释:不存在满足题意的三元组
示例 3:
输入:nums = [2,1,5,0,4,6]
输出:true
解释:三元组 (3, 4, 5) 满足题意,因为 nums[3] == 0 < nums[4] == 4 < nums[5] == 6
提示:
1 <= nums.length <= 5 * 105
-231 <= nums[i] <= 231 - 1
bool increasingTriplet(vector<int>& nums) {
int c1 = INT_MAX, c2 = INT_MAX;
for (int x : nums) {
if (x <= c1) {
c1 = x; // c1 is min seen so far (it's a candidate for 1st element)
} else if (x <= c2) { // here when x > c1, i.e. x might be either c2 or c3
c2 = x; // x is better than the current c2, store it
} else { // here when we have/had c1 < c2 already and x > c2
return true; // the increasing subsequence of 3 elements exists
}
}
return false;
}
Solution1 贪心

Solution2 双向遍历

class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
int n = nums.size();
if (n < 3) {
return false;
}
vector<int> leftMin(n);
leftMin[0] = nums[0];
for (int i = 1; i < n; i++) {
leftMin[i] = min(leftMin[i - 1], nums[i]);
}
vector<int> rightMax(n);
rightMax[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; i--) {
rightMax[i] = max(rightMax[i + 1], nums[i]);
}
for (int i = 1; i < n - 1; i++) {
if (nums[i] > leftMin[i - 1] && nums[i] < rightMax[i + 1]) {
return true;
}
}
return false;
}
};
复杂度分析
时间复杂度:O(n),其中 nn 是数组 \textit{nums}nums 的长度。需要遍历数组三次。
空间复杂度:O(n),其中 nn 是数组 \textit{nums}nums 的长度。需要创建两个长度为 nn 的数组 \textit{leftMin}leftMin 和 \textit{rightMax}rightMax。
344. 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = [“h”,“e”,“l”,“l”,“o”]
输出:[“o”,“l”,“l”,“e”,“h”]
示例 2:
输入:s = [“H”,“a”,“n”,“n”,“a”,“h”]
输出:[“h”,“a”,“n”,“n”,“a”,“H”]
We use here two pointers that gives us access to characters for swapping in left and right side of the string. For swapping we use a convinient C++ method swap. We just iterate over characters and swap them.
Time: O(n)
Space: O(1)
Solution1 双指针交换
class Solution {
public:
void reverseString(vector<char>& s) {
for (int i = 0, j = s.size() - 1; i < s.size()/2; i++, j--) {
swap(s[i],s[j]);
}
}
};
堆:347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
提示:
1 <= nums.length <= 105
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一,换句话说,数组中前 k 个高频元素的集合是唯一的
进阶:你所设计算法的时间复杂度 必须 优于 O(n log n) ,其中 n 是数组大小。
How's going Ladies - n - Gentlemen, today we are going to solve another coolest problem i.e. Top K Frequent Elements
Okay, so in order to solve this problem, first of all let's understand what the problem statement is:
Given an integer array nums,
and an integer k, return the k most frequent elements. You may return the answer in any order.
Okay, so wait wait listen just looking at this if you know the HashMap, you'll simply gonna say we can solve this problem easily using HashMap. And I'll say yes, exactly we gonna do the exact same thing but we will use Heap as well with HashMap, if you got the idea by listening heap. Then you had just solve the brute force approach
So, let's talk about it's
Brute Force Approach :-
Let's take an example,
Input: nums = [1,1,1,2,2,3], k = 2
Output: [1,2]
So, we have 2 step's to perform in this problem:-
HashMap
Heap
Step -1 :- Make an Frequency map & fill it with the given elements
[1,1,1,2,2,3]
------------------------------------------------
| 1 ---> | 3 |
| | |
| 2 ---> | 2 | HashMap of Integer, Integer
| | |
| 3 ---> | 1 |
------------------------------------------------
Okay, so we just had completed our step no.1 now, it;s time to move to next step
Step -2 :- Make an MaxHeap & fill it with keys & on the peek of our Heap we will be having most frequent elements
HashMap :-
Key Value
1 ----> 3
2 ----> 2
3 ----> 1
Heap :-
| 1 | from the top of the heap we'll pop that no. of element requires in our array of k size
| 2 |
| 3 |
------------
Create result array res & store K frequent elements in it.
Heap :-
| | res : [1]
| 2 |
| 3 |
------------
Heap :-
| | res : [1, 2]
| |
| 3 |
------------
As, our K is 2 we gonna only store Most frequent K elements in our array, therefore in the result we get:- [1, 2]
I hope so, ladies - n - gentlemen, this approach is absolute clear, Let's code it, up
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> map = new HashMap<>();
for(int i : nums){
map.put(i, map.getOrDefault(i, 0) + 1);
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a,b) -> map.get(b) - map.get(a));
for(int key : map.keySet()){
maxHeap.add(key);
}
int res[] = new int[k];
for(int i = 0; i < k; i++){
res[i] = maxHeap.poll();
}
return res;
}
}
ANALYSIS :-
Time Complexity :- BigO(K log D) as we are Poll K distinct elements from the Heap & here D is no. of distinct (unique) elements in the input array
Space Complexity :- BigO(D), this is the size of the heap.
Well, this is not a super efficient Approach,
We can solve this more efficiently as well, now some of you'll ask but how!!
Well, for that we have Bucket Sorting
Optimize Approach :-
Let's understand what bucket sort is,
Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
In this process we gonna follow 3 major steps :-
Step - 1 :
Create Frequency map:
1.1 Iterate thru the given nums[] array
1.2. With each iteration - check if map already contains current key
If current key is already in the map just increase the value for this key
Else add key value pair.
Where key is current int and value is 1 (1 -> we encounter given key for the first time)
image
Step - 2 :
Create Bucket List[]:
index of bucket[] arr will represent the value from our map
Why not use int[] arr? Multiple values can have the same frequency that's why we use List[] array of lists instead of regular array
Iterate thrue the map and for each value add key at the index of that value
image
Step - 3 :
If we look at bucket arr we can see that most frequent elements are located at the end of arr
and leat frequent elemnts at the begining
Last step is to iterate from the end to the begining of the arr and add elements to result List
image
I hope so ladies - n - gentlemen Approach is absolute clear, Let's code it up
Solution1 排序法
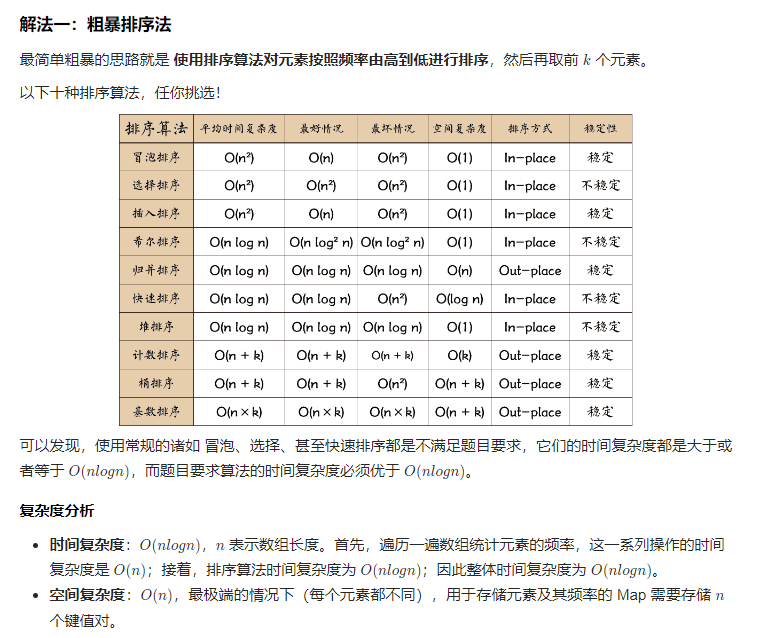
Solution2 最小堆法
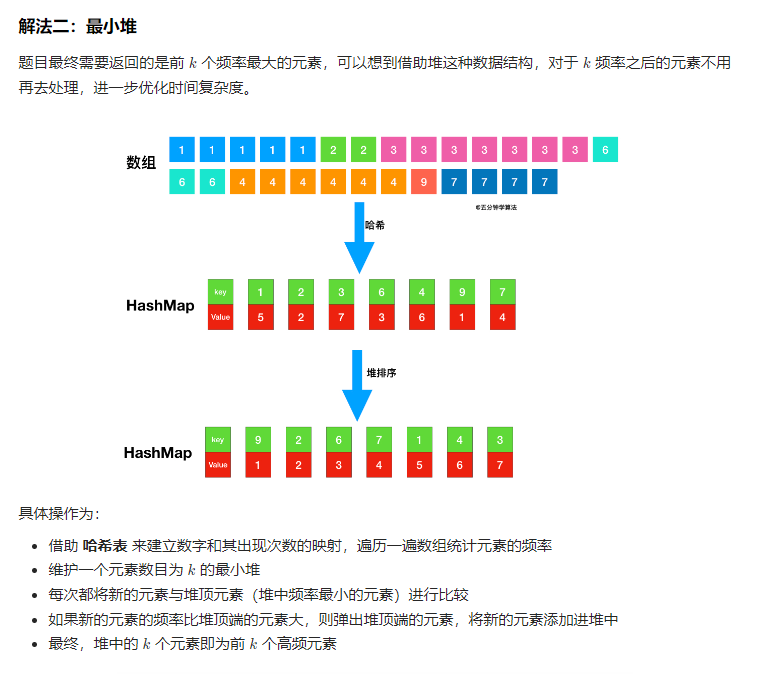
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
vector<int> res;
map<int, int> freq;
using pii = std::pair<int, int>;
priority_queue<pii, vector<pii>, greater<pii>> pq;
for (auto e : nums) ++freq[e];
for (auto& pair : freq) {
pq.emplace(pair.second, pair.first);
if (pq.size() > k) pq.pop();
}
while (!pq.empty()) {
res.emplace_back(pq.top().second);
pq.pop();
}
return res;
}
};
349. 两个数组的交集
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的
Approach 1: Two Sets
Intuition
The naive approach would be to iterate along the first array nums1 and to check for each value if this value in nums2 or not. If yes - add the value to output. Such an approach would result in a pretty bad \mathcal{O}(n \times m)O(n×m) time complexity, where n and m are arrays' lengths.
To solve the problem in linear time, let's use the structure set, which provides in/contains operation in \mathcal{O}(1)O(1) time in average case.
The idea is to convert both arrays into sets, and then iterate over the smallest set checking the presence of each element in the larger set. Time complexity of this approach is \mathcal{O}(n + m)O(n+m) in the average case.
Solution1
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果,之所以用set是为了给结果集去重
int hash[1005] = {0}; // 默认数值为0
for (int num : nums1) { // nums1中出现的字母在hash数组中做记录
hash[num] = 1;
}
for (int num : nums2) { // nums2中出现话,result记录
if (hash[num] == 1) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};
Solution2
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 发现nums2的元素 在nums_set里又出现过
if (nums_set.find(num) != nums_set.end()) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};
378. 有序矩阵中第 K 小的元素
给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
你必须找到一个内存复杂度优于 O(n2) 的解决方案。
示例 1:
输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出:13
解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13
示例 2:
输入:matrix = [[-5]], k = 1
输出:-5
提示:
n == matrix.length
n == matrix[i].length
1 <= n <= 300
-109 <= matrix[i][j] <= 109
题目数据 保证 matrix 中的所有行和列都按 非递减顺序 排列
1 <= k <= n2
进阶:
你能否用一个恒定的内存(即 O(1) 内存复杂度)来解决这个问题?
你能在 O(n) 的时间复杂度下解决这个问题吗?这个方法对于面试来说可能太超前了,但是你会发现阅读这篇文章( this paper )很有趣。
✔️ Solution 1: Max Heap keeps up to k elements
The easy approach is that we iterate all elements in the matrix and and add elements into the maxHeap. The maxHeap will keep up to k smallest elements (because when maxHeap is over size of k, we do remove the top of maxHeap which is the largest one). Finally, the top of the maxHeap is the kth smallest element in the matrix.
This approach leads this problem become the same with 215. Kth Largest Element in an Array, which doesn't take the advantage that the matrix is already sorted by rows and by columns.
Complexity:
Time: O(M * N * logK), where M <= 300 is the number of rows, N <= 300 is the number of columns.
Space: O(K), space for heap which stores up to k elements.
✔️ Solution 2: Min Heap to find kth smallest element from amongst N sorted list
Since each of the rows in matrix are already sorted, we can understand the problem as finding the kth smallest element from amongst M sorted rows.
We start the pointers to point to the beginning of each rows, then we iterate k times, for each time ith, the top of the minHeap is the ith smallest element in the matrix. We pop the top from the minHeap then add the next element which has the same row with that top to the minHeap.
Solution1 暴力
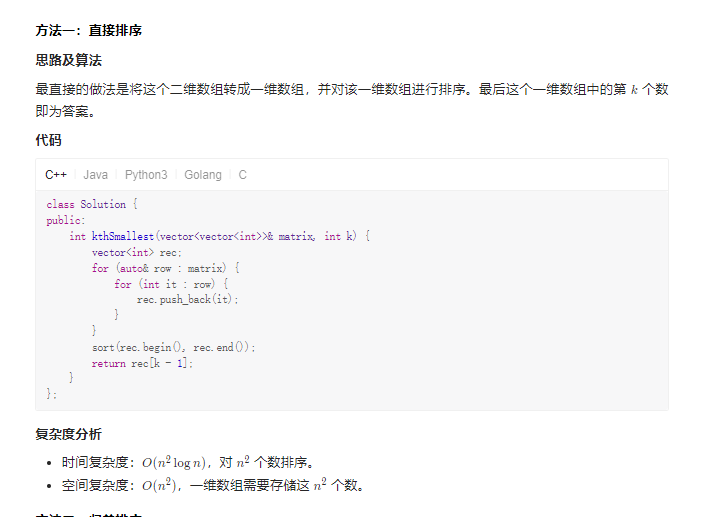
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
struct point {
int val, x, y;
point(int val, int x, int y) : val(val), x(x), y(y) {}
bool operator> (const point& a) const { return this->val > a.val; }
};
priority_queue<point, vector<point>, greater<point>> que;
int n = matrix.size();
for (int i = 0; i < n; i++) {
que.emplace(matrix[i][0], i, 0);
}
for (int i = 0; i < k - 1; i++) {
point now = que.top();
que.pop();
if (now.y != n - 1) {
que.emplace(matrix[now.x][now.y + 1], now.x, now.y + 1);
}
}
return que.top().val;
}
};
Solution2 最小堆


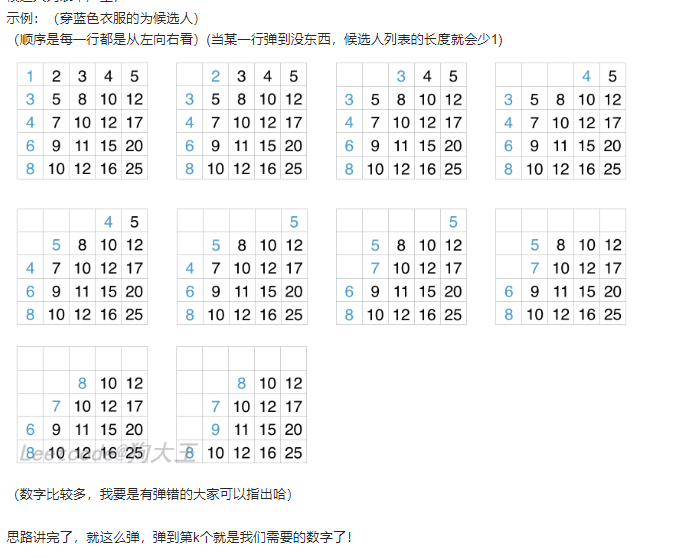
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = “3[a]2[bc]”
输出:“aaabcbc”
示例 2:
输入:s = “3[a2[c]]”
输出:“accaccacc”
示例 3:
输入:s = “2[abc]3[cd]ef”
输出:“abcabccdcdcdef”
示例 4:
输入:s = “abc3[cd]xyz”
输出:“abccdcdcdxyz”
提示:
1 <= s.length <= 30
s 由小写英文字母、数字和方括号 ‘[]’ 组成
s 保证是一个 有效 的输入。
s 中所有整数的取值范围为 [1, 300]
This is the standard solution given under the tab 'Solution' of the same problem: https://leetcode.com/problems/decode-string/solution/
We start with the original string s and index = 0. If the index is not ']', meaning its a digit or alphabet (but not '[' -> this is ensured in the later part of the code). Also note that the string won't start with '[' so there is no chance of having it initially.
First lets take the case when the string isdigit. In that case, count the number of times the inner string need to be repeated. For example 26[X], string X will be repeated 26 times and 26 is stored in k. Now increment the index -> this is done as we know that number will be accompanied by [.
Now recurse on the inner string s and also increment index, this time for ]. While recursing for inner string, if the character is not digit, we store that and return it as a string. Now remember this inner string needs to be repeated 'k' times so we add that to current return string 'ret'. Return the ret string.
Solution1 两个栈

402. 移掉 K 位数字
给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k 位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。
示例 1 :
输入:num = “1432219”, k = 3
输出:“1219”
解释:移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。
示例 2 :
输入:num = “10200”, k = 1
输出:“200”
解释:移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入:num = “10”, k = 2
输出:“0”
解释:从原数字移除所有的数字,剩余为空就是 0 。
提示:
1 <= k <= num.length <= 105
num 仅由若干位数字(0 - 9)组成
除了 0 本身之外,num 不含任何前导零
KNOCKCAT
1. Easy C++
2. Line by Line Explanation with Comments.
3. Detailed Explanation ✅
4. Handwritten snap of an TestCase at the end of code given.
5. Please Upvote if it helps⬆️
6. Link to my Github Profile contains a repository of Leetcode with all my Solutions. ⬇️
LeetCode
EXPLANATION
1. Deleting k digits means keeping n - k digits, where n is the total number of digits.
2. Use a stack that you keep sorted ascendingly. You remove elements from it as long as you can still make it to n - k digits,
and your current element is smaller than the top of the stack:
push(2) => 2
push(4) because 2 < 4 => 24
push(6) because 4 < 6 => 246
pop() because 3 < 6 and we can still end up with 2 digits => 24
pop() for the same reason => 2
push(3) => 23
push(5) => 235
Then just take the first k digits => 23. Or you can make sure never to push more than k digits, and then the final stack is your solution.
3. Note that you cannot pop elements if that means you will not be able to build a solution of k digits.
For this, you need to check the current number of elements in the stack and the number of digits to the right of your current position on the input number.
Some More Points
1. Approach is simple. We need a number which is minimum, thus we need to remove the most significant digits first.
For eg. if we have a number having digits 1-4 then 1234 would be the minimum and not 2314 or anything else.
So in case of 2314, we remove 3 first, and then we go for 2 (Because they are more significant than 4). Observing this simple idea,
we need to remove any digit which is greater than its following digit. Thats why we deleted 3 as it,
was greater than 1 and similiarly 2 as it was also greater than 1.
2. In order to accomplish this, we use stack Data Structure where we pop the top if it is greater than current digit.
3. The conditions mentioned in while loop are important to avoid any Runtime Error. For eg. ["10001" 2] the answer is "0" but if we don't
mention the condition !s.empty(), then the while loop will run on empty stack and try to pop the top which doesn't exist thus throwing RE.
Time Complexity :- O(N) // as we only traversing the string for once
Space complexity:- O(N) // as we will store maximum of n digits in our string
Solution1 贪心+单调栈

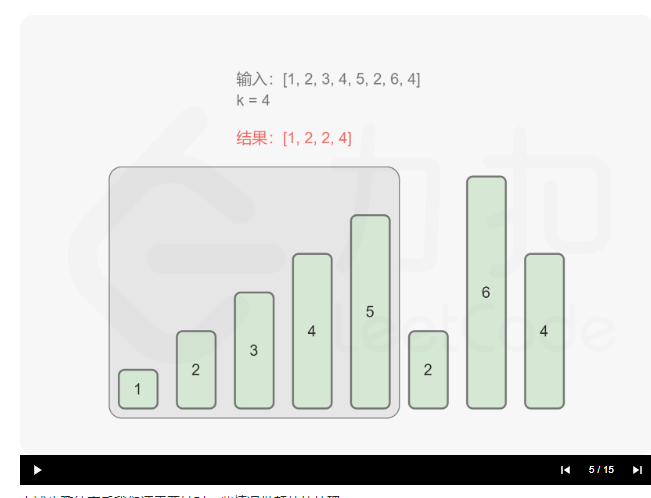
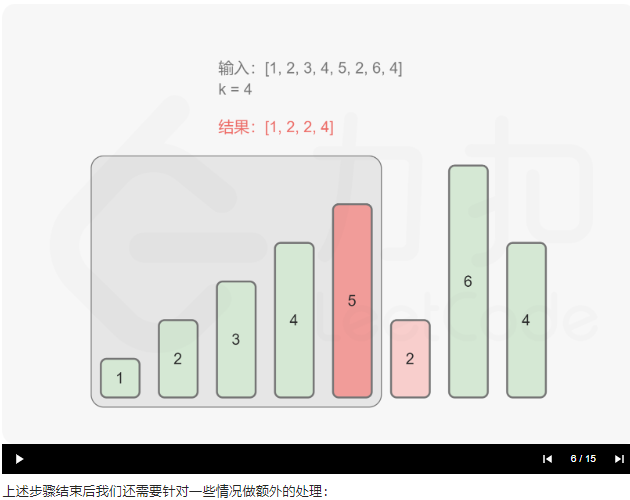
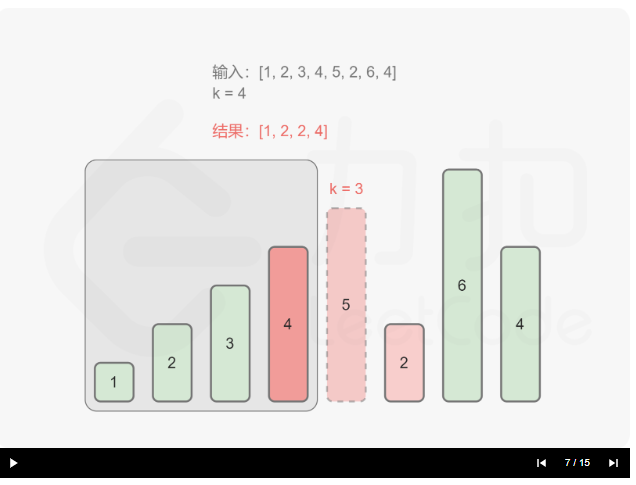
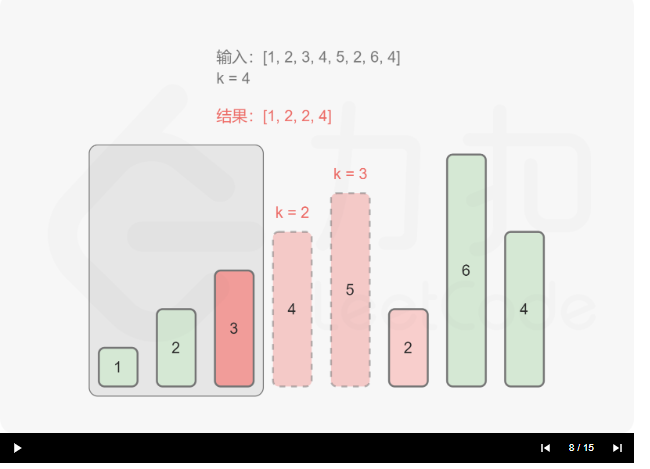
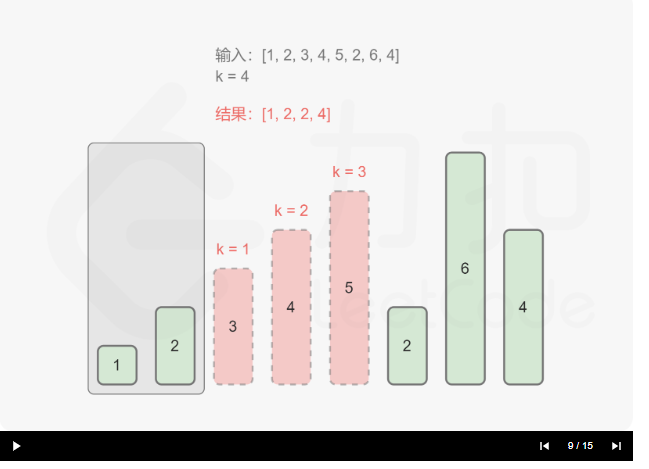



406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 2000
0 <= hi <= 106
0 <= ki < people.length
题目数据确保队列可以被重建
Time Complexity : O(N^2) , Space Complexity : O(N)
Upvote if Found Helpful
Intuition :
So here if we carefully observe we can notice that if we take any person and insert any other shorter person before or after him in queue then the number of people higher or equal to him before him doesn't change. So we need to place the taller people first in the queue and we can add the shorter people in between or after them according to reqirement.
So we need to sort the array according to their height in decreasing order (Heighest at the first).
Now think if 2 person has same height the person with lower (Ki) will be inserted before other. Because The person before will have at least 1 less number of equal or taller people before him than who is after.
So in case of equal heights (Hi) the person with lesser (Ki) will be placed first during sorting.
Now if we insert the person from the sorted array in the ans array in the position (Ki) then the people greater than or equal to him will be in his left and they total will be (Ki) in number (From 0 to (Ki-1)th position). After that whatever we insert will be shorter (Which doesn't matter if inserted after or before the position) or if equal will have greater (Ki) than the present one i.e. will be inserted in the right.
So for each element in the sorted array we insert it at the (Ki)th position in the ans array.
Example :
People = [[7,0], [4,4], [7,2], [5,0], [6,1], [5,4], [8,0]]
Sorted People accordin to comp function : [[8,0], [7,0], [7,2], [6,1], [5,0], [5,4], [4,4]]]
Now for each iteration in the loop ; (Ki of each man is included in ' ', and each inserted man in " ")
man = [8,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[8,0]"]
man = [7,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[7,0]", [8,0]]
man = [7,'2'] -> ans.insert(ans.begin()+'2', man) -> ans = [[7,0], [8,0], "[7,2]"]
man = [6,'1'] -> ans.insert(ans.begin()+'1', man) -> ans = [[7,0], "[6,1]", [8,0], [7,2]]
man = [5,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[5,0]", [7,0], [6,1], [8,0], [7,2]]
man = [5,'4'] -> ans.insert(ans.begin()+'4', man) -> ans = [[5,0], [7,0], [6,1], [8,0], "[5,4]", [7,2]]
man = [4,'4'] -> ans.insert(ans.begin()+'4', man) -> ans = [[5,0], [7,0], [6,1], [8,0], "[4,4]", [5,4], [7,2]]
See the final ans array fullfills all the conditions.
Solution1 先排序 再插队
class Solution {
public:
static bool cmp(const vector<int> a,const vector<int> b){
if (a[0] > b[0]) return true;
if (a[0] == b[0] && a[1] < b[1]) return true;
return false;
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
vector<vector<int >> res;
sort(people.begin(),people.end(),cmp);
for(auto val:people){
res.insert(res.begin()+val[1],val);
}
return res;
}
};
409. 最长回文串
给定一个包含大写字母和小写字母的字符串 s ,返回 通过这些字母构造成的 最长的回文串 。
在构造过程中,请注意 区分大小写 。比如 “Aa” 不能当做一个回文字符串。
示例 1:
输入:s = “abccccdd”
输出:7
解释:
我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。
示例 2:
输入:s = “a”
输入:1
提示:
1 <= s.length <= 2000
s 只由小写 和/或 大写英文字母组成
Approach #1: Greedy [Accepted]
Intuition
A palindrome consists of letters with equal partners, plus possibly a unique center (without a partner). The letter i from the left has its partner i from the right. For example in 'abcba', 'aa' and 'bb' are partners, and 'c' is a unique center.
Imagine we built our palindrome. It consists of as many partnered letters as possible, plus a unique center if possible. This motivates a greedy approach.
Algorithm
For each letter, say it occurs v times. We know we have v // 2 * 2 letters that can be partnered for sure. For example, if we have 'aaaaa', then we could have 'aaaa' partnered, which is 5 // 2 * 2 = 4 letters partnered.
At the end, if there was any v % 2 == 1, then that letter could have been a unique center. Otherwise, every letter was partnered. To perform this check, we will check for v % 2 == 1 and ans % 2 == 0, the latter meaning we haven't yet added a unique center to the answer.
Complexity Analysis
Time Complexity: O(N)O(N), where NN is the length of s. We need to count each letter.
Space Complexity: O(1)O(1), the space for our count, as the alphabet size of s is fixed. We should also consider that in a bit complexity model, technically we need O(\log N)O(logN) bits to store the count values.
Solution1
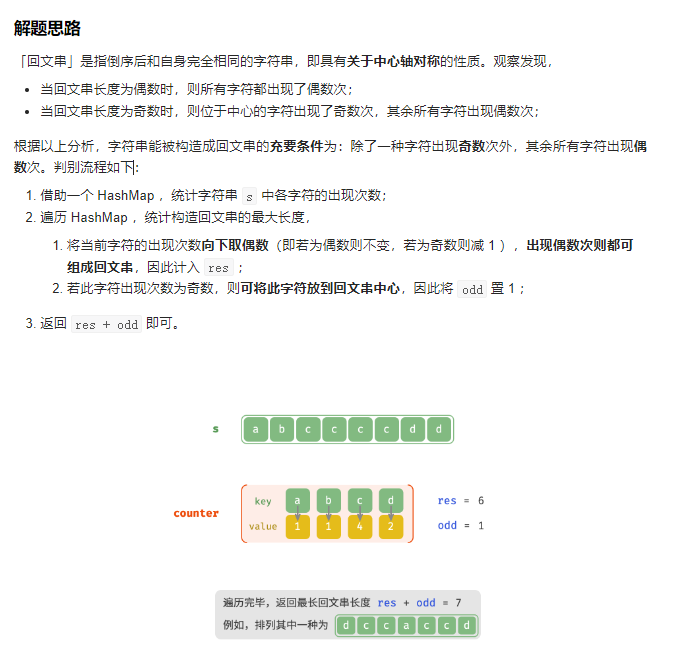
415. 字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = “11”, num2 = “123”
输出:“134”
示例 2:
输入:num1 = “456”, num2 = “77”
输出:“533”
示例 3:
输入:num1 = “0”, num2 = “0”
输出:“0”
提示:
1 <= num1.length, num2.length <= 104
num1 和num2 都只包含数字 0-9
num1 和num2 都不包含任何前导零
26
DBabichev's avatar
DBabichev
35937
Last Edit: August 9, 2021 10:37 PM
1.2K VIEWS
What we need to do in this problem is to perform usual schoolbook addition. We need to start to add numbers from the last elements and take care of carry and cases when one number has more digits that another. Imagine that we want to add two numbers: 986 and 47. Then we have the followint steps:
Add 6 and 7, so we have digit 3 and carry equal to 1.
Add 8 and 4 and 1, so we have 3 and carry equal to 1.
Add 9 from first number, and we do not have anything from second, so we choose 0 from second. Also we have curry equal to 1, finally we have digit 0 and carry equal to 1.
We still have carry, but no digits left, so we evaluate 0 + 0 + 1 = 1. And now we can stop, we do not have digits and we do not have carry.
Final number we constructed is 1033.
Complexity
Time complexity is O(m + n), where m and n are lengths of our linked lists, space complexity is O(max(m, n)) if we count answer as memory or O(1) if we do not.
Solution1

class Solution {
public:
string addStrings(string num1, string num2) {
int i = num1.length() - 1, j = num2.length() - 1, add = 0;
string ans = "";
while (i >= 0 || j >= 0 || add != 0) {
int x = i >= 0 ? num1[i] - '0' : 0;
int y = j >= 0 ? num2[j] - '0' : 0;
int result = x + y + add;
ans.push_back('0' + result % 10);
add = result / 10;
i -= 1;
j -= 1;
}
// 计算完以后的答案需要翻转过来
reverse(ans.begin(), ans.end());
return ans;
}
};

求1+2+…n


求滑动窗口的最大值

扑克牌中的顺子


左旋转字符串
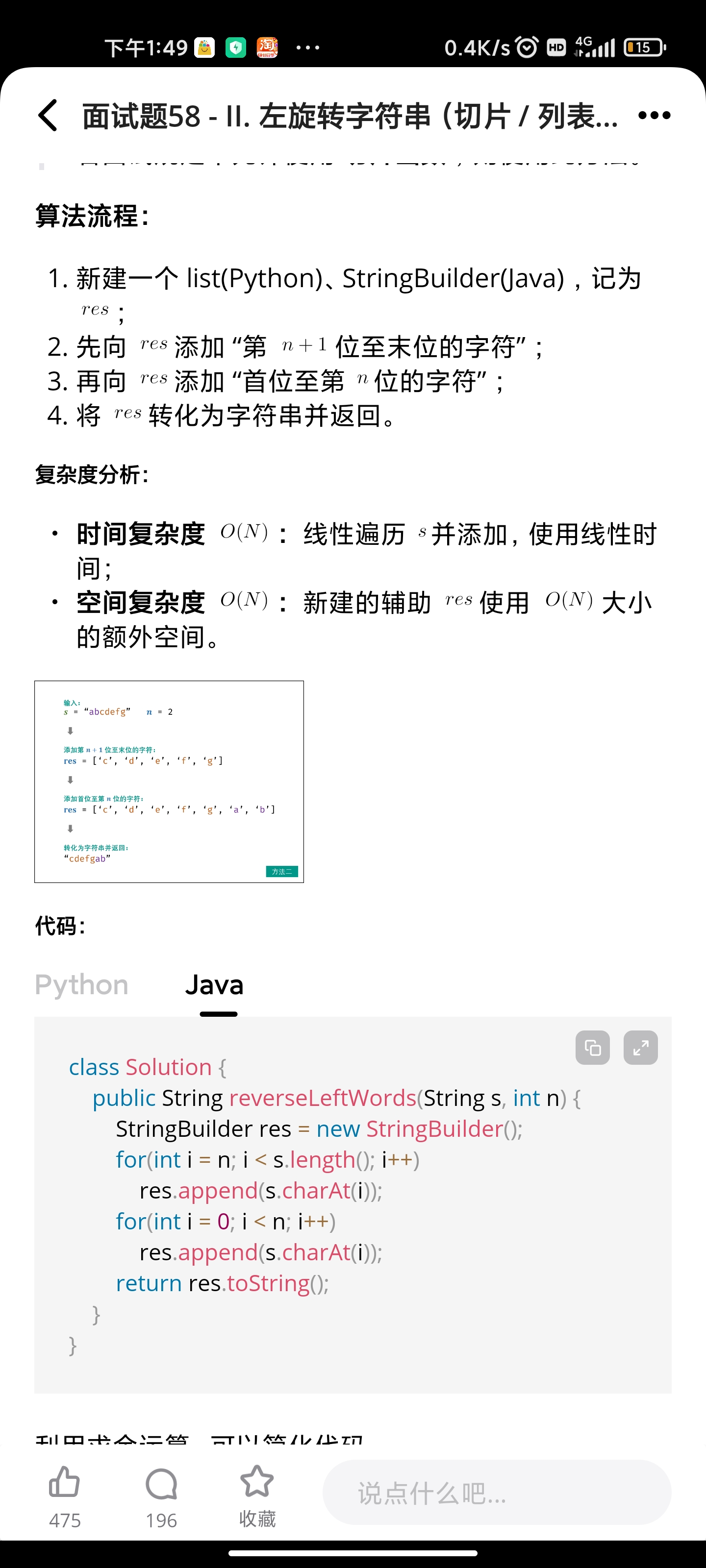
最长不含重复字符的子字符串

滑动窗口的最大值

和为s连续正数序列

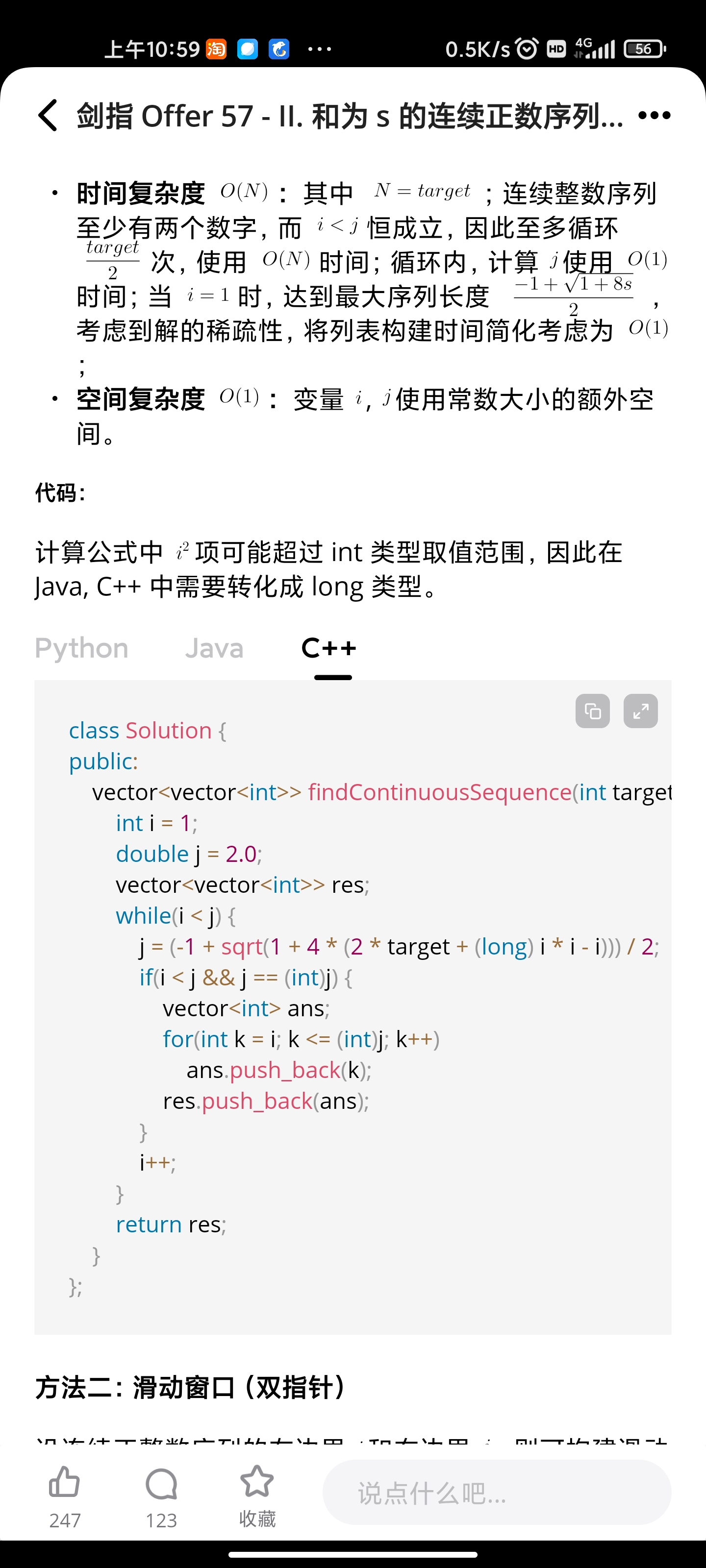

翻转单词顺序

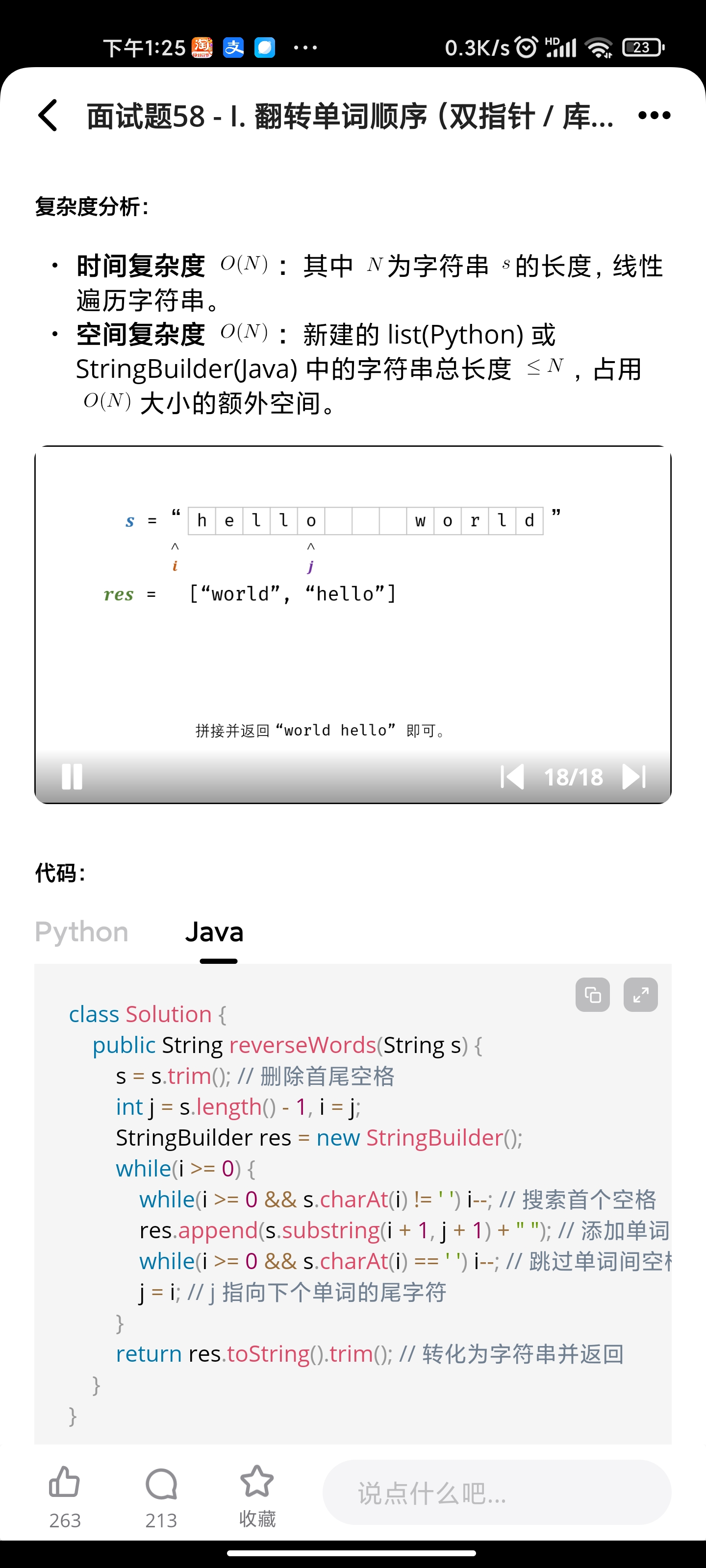
左旋转字符串

和为s的两个数字

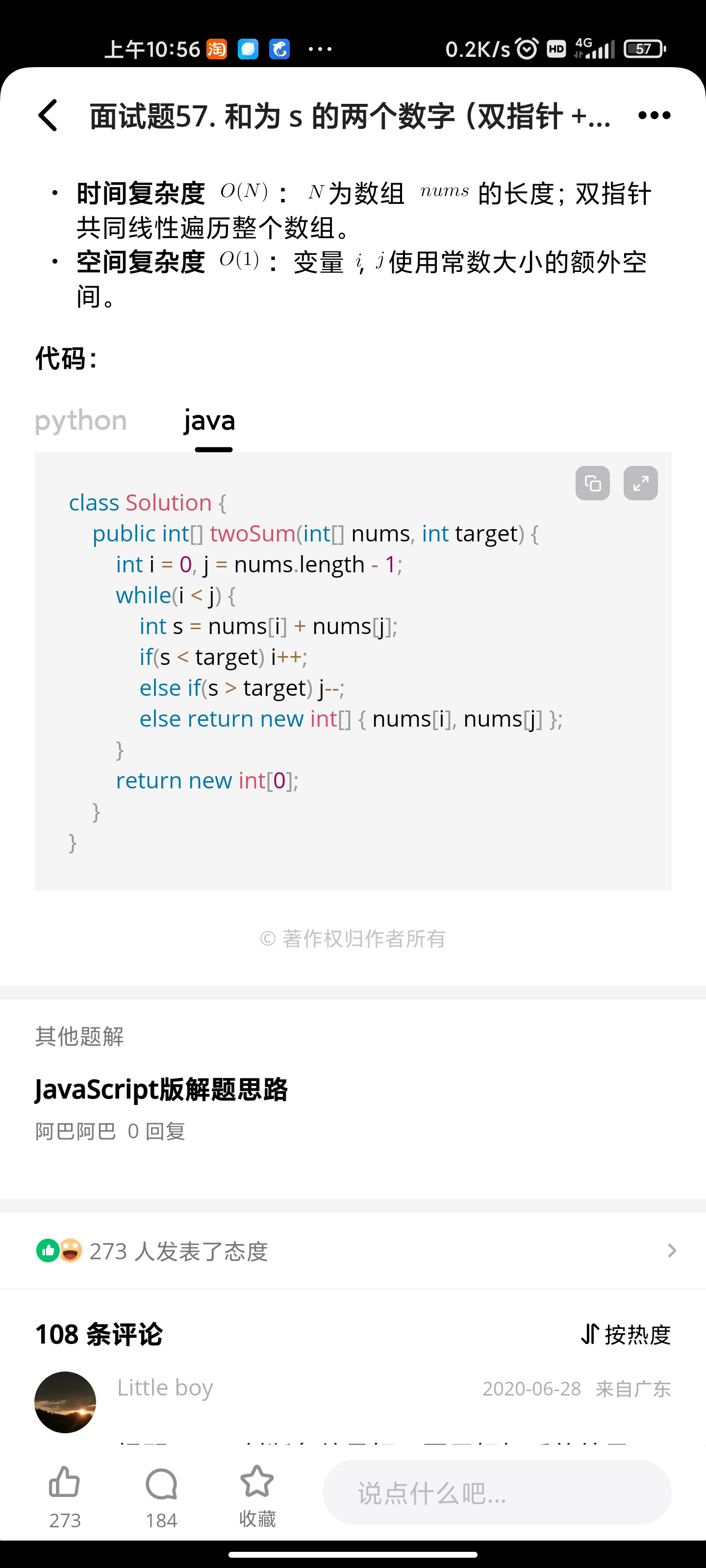
数组中出现次数超过一半的次数


第一个只出现一次的字符


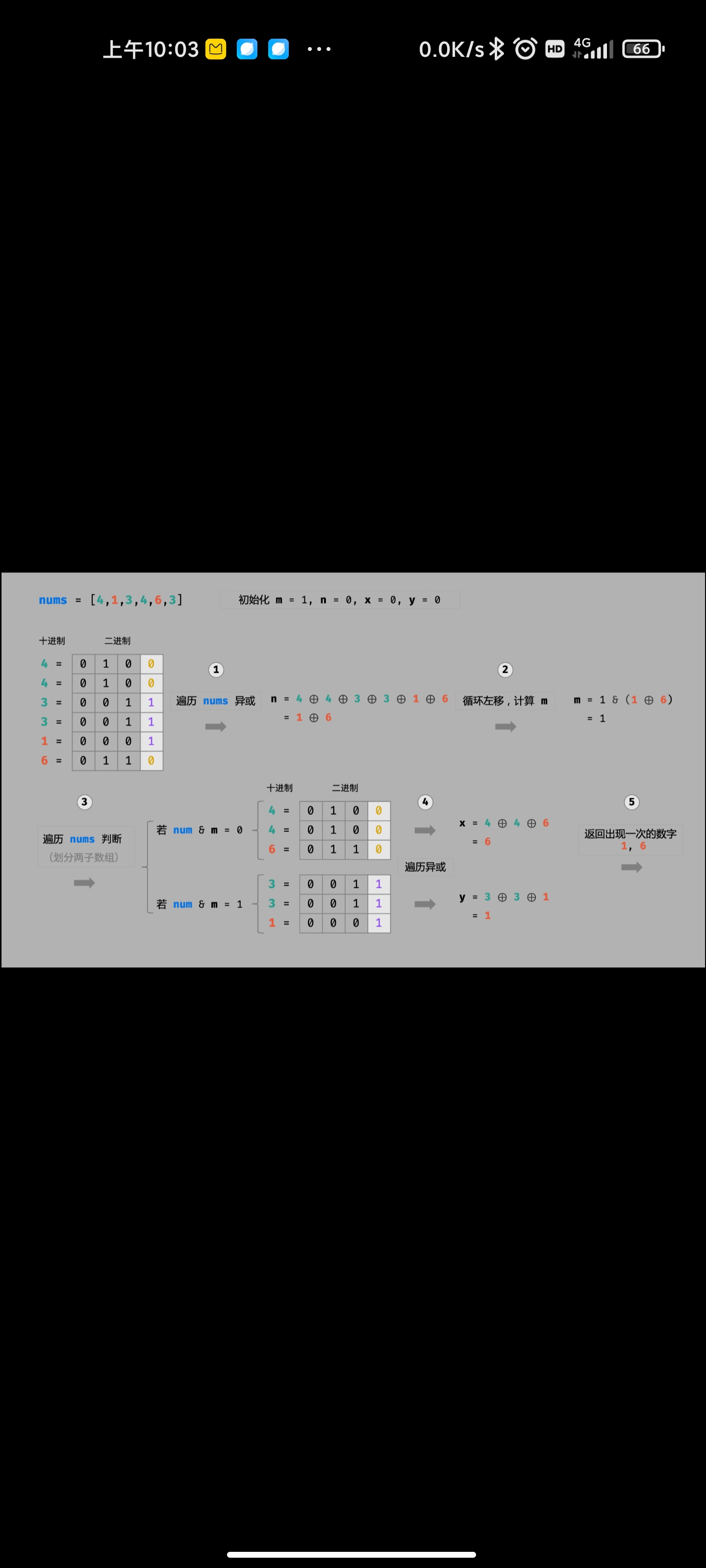

栈的压入、弹出序列

包含min函数的栈
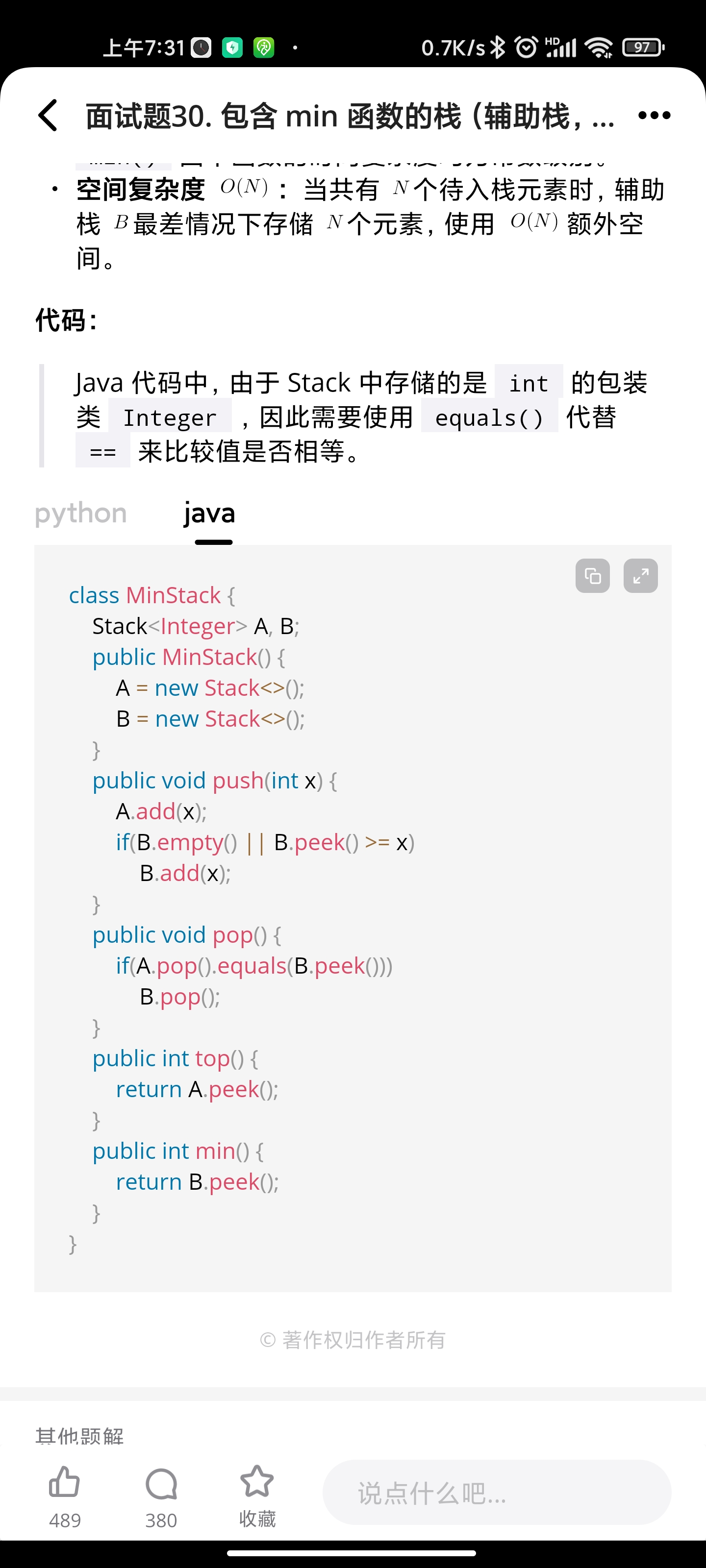
反转链表
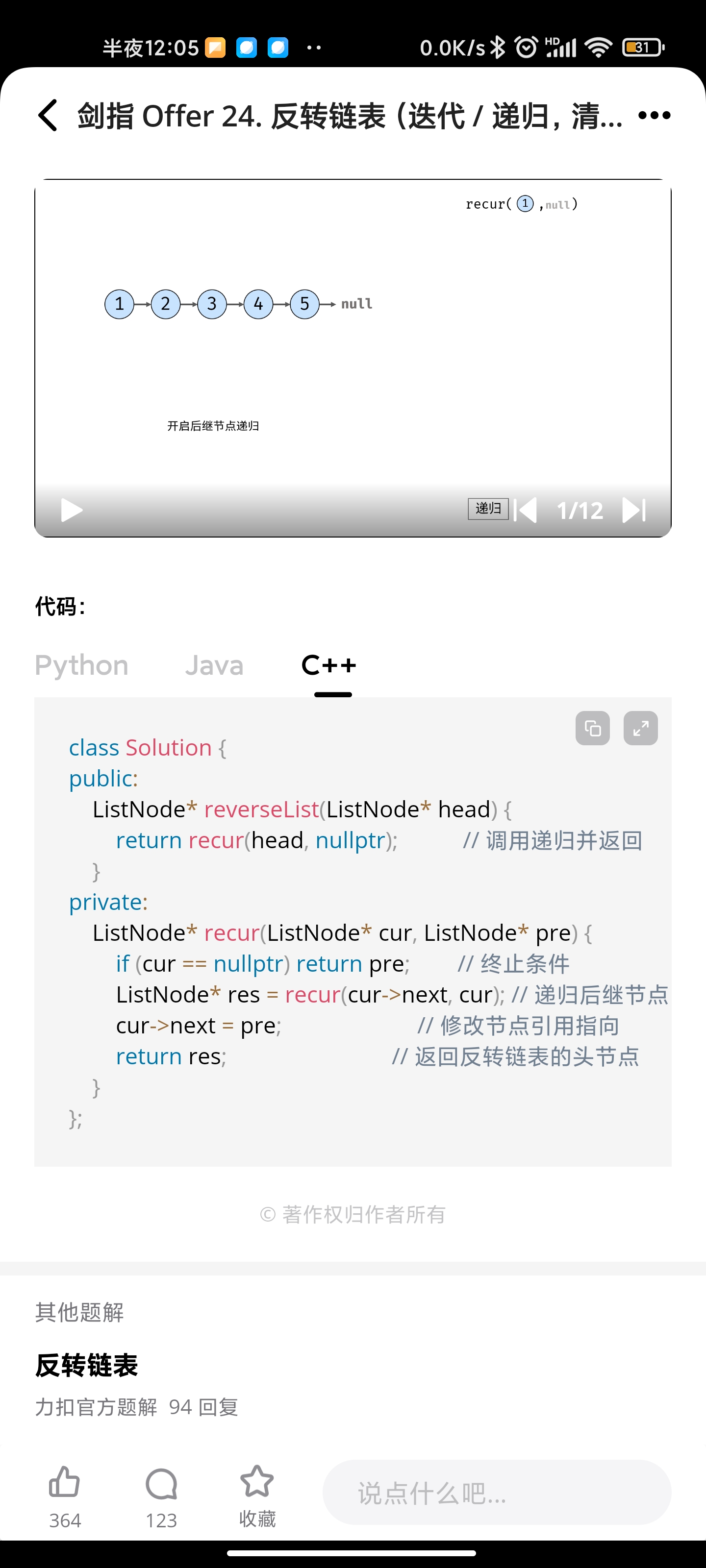
数值的整数次方


删除链表的节点
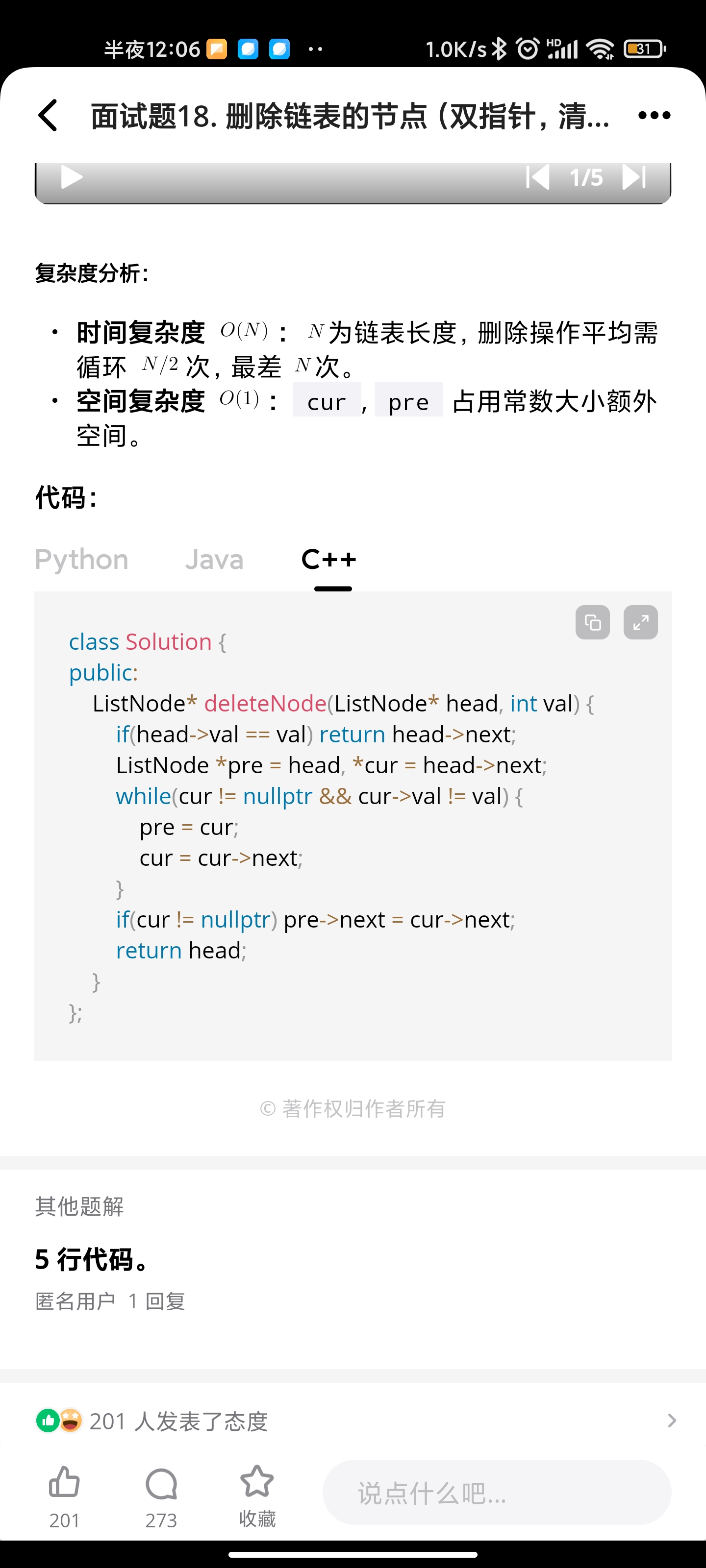
链表的倒数第K个节点


顺时针打印矩阵
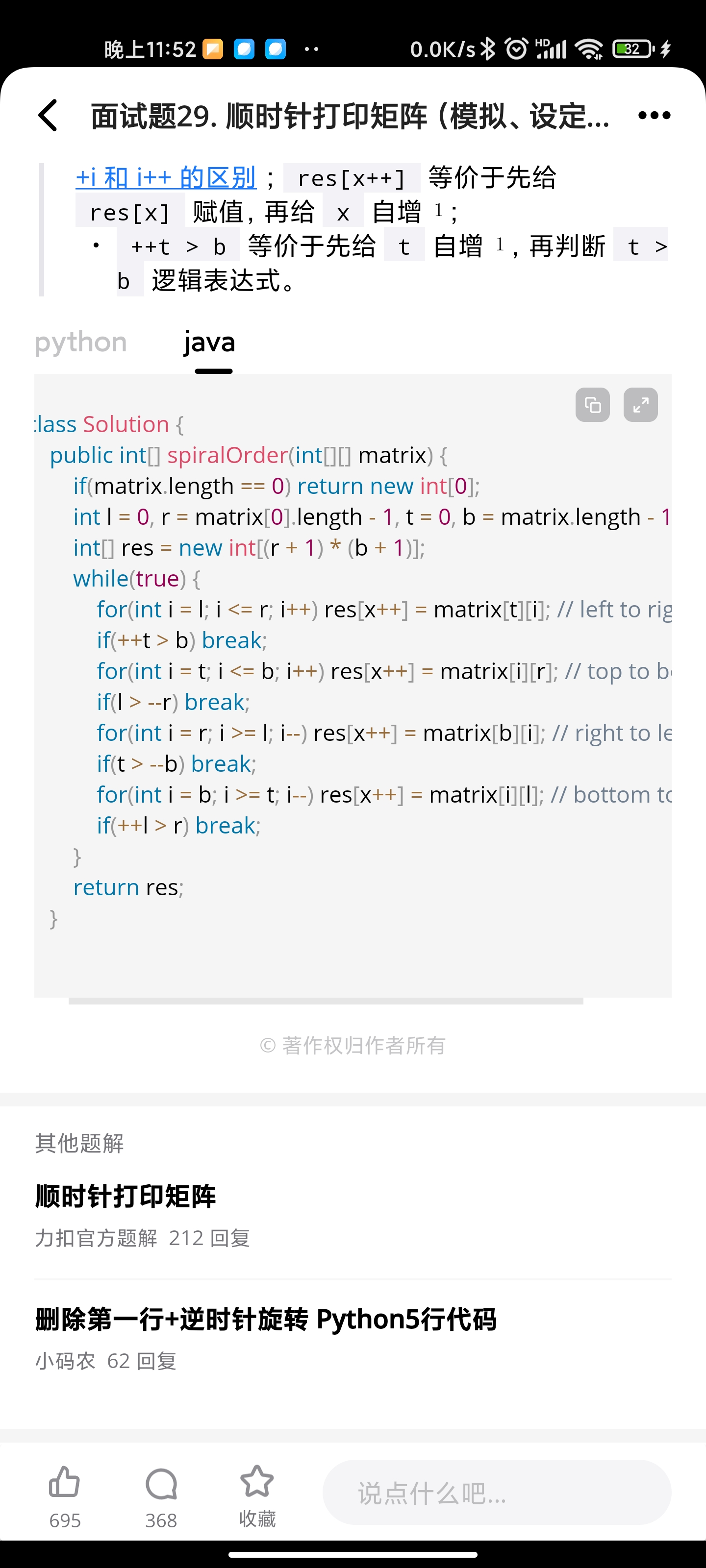


调整数组顺序使得奇数位于偶数前

合并两个排序的链表

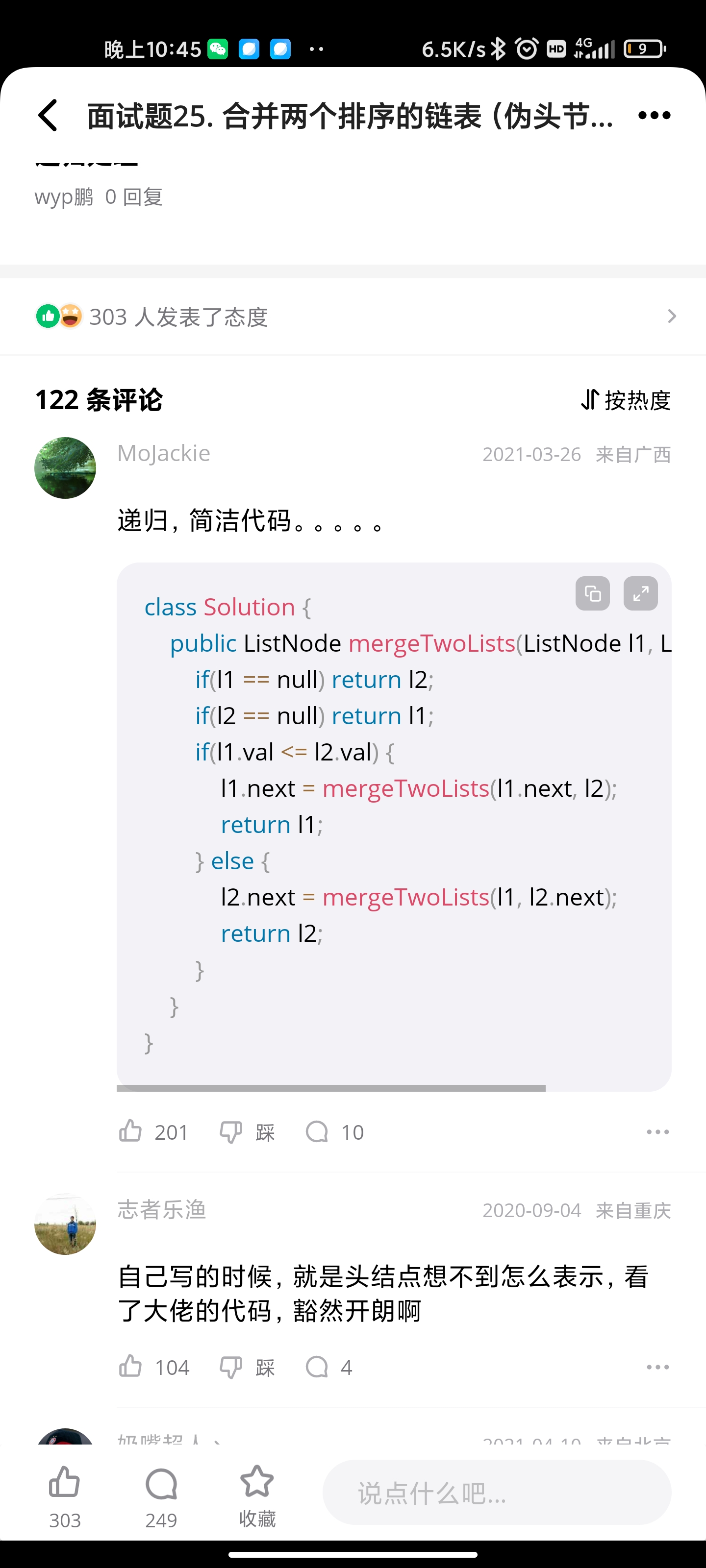
从尾到头打印链表

替换空格
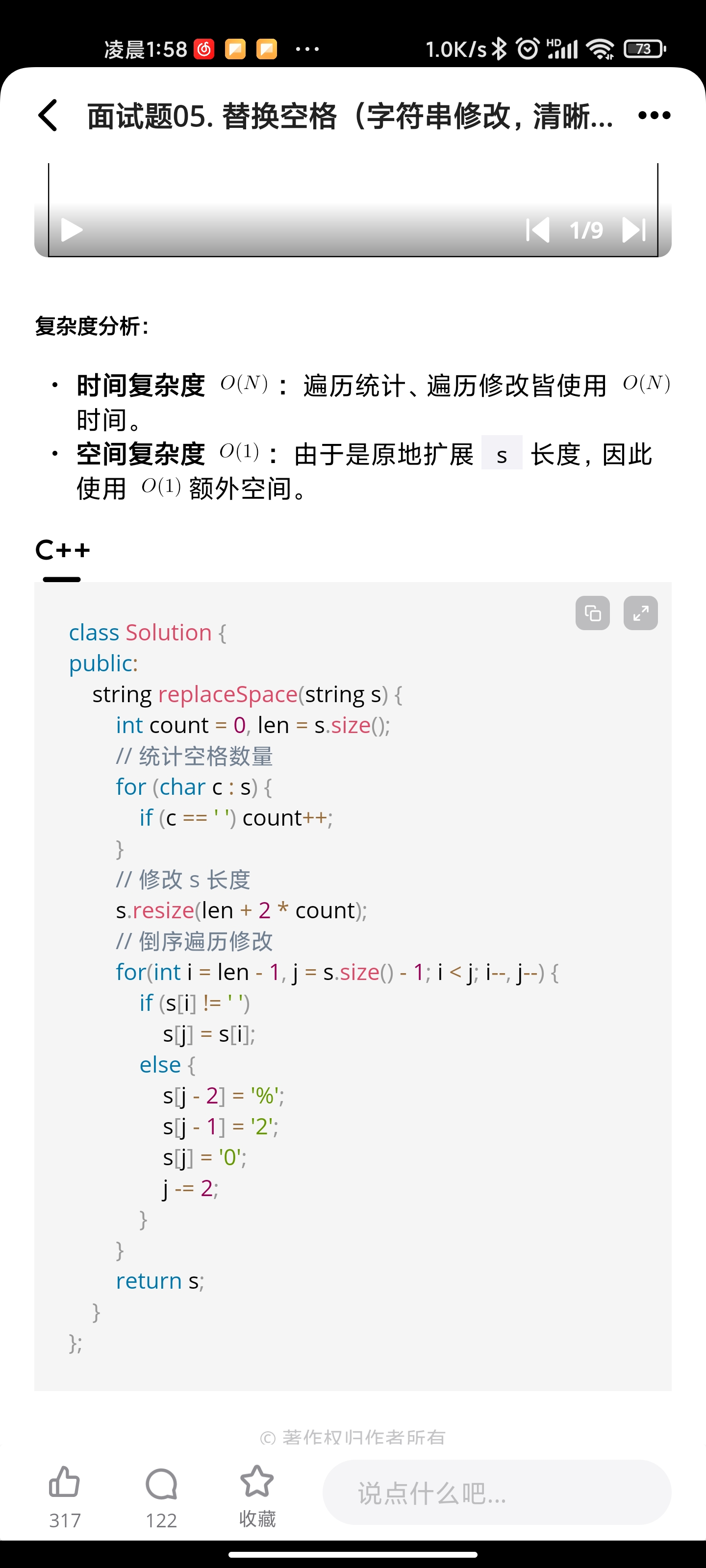


重构字符串
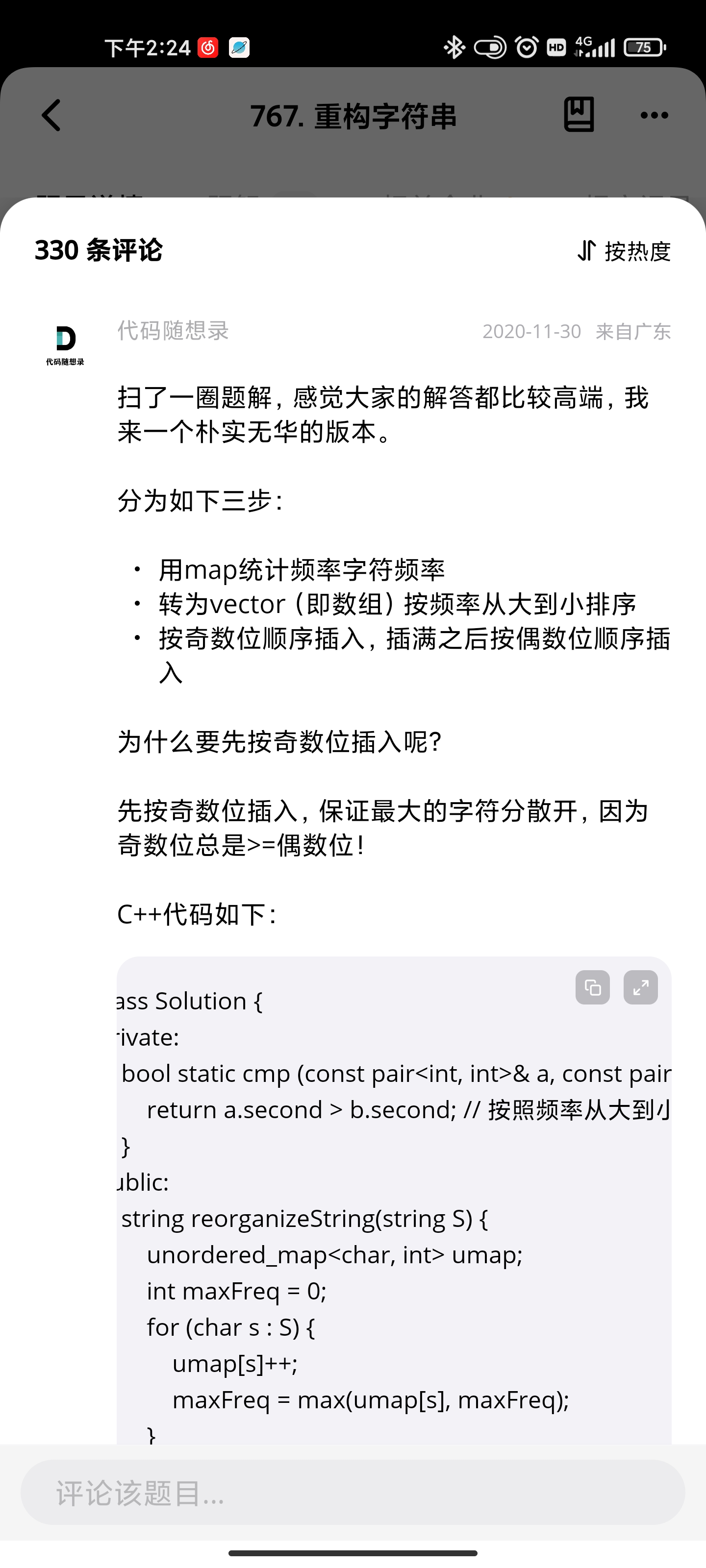

数组中重复的数字




自除数
Approach #1: Brute Force [Accepted]
Intuition and Algorithm
For each number in the given range, we will directly test if that number is self-dividing.
By definition, we want to test each whether each digit is non-zero and divides the number. For example, with 128, we want to test d != 0 && 128 % d == 0 for d = 1, 2, 8. To do that, we need to iterate over each digit of the number.
A straightforward approach to that problem would be to convert the number into a character array (string in Python), and then convert back to integer to perform the modulo operation when checking n % d == 0.
We could also continually divide the number by 10 and peek at the last digit. That is shown as a variation in a comment.
Complexity Analysis
Time Complexity: O(D)O(D), where DD is the number of integers in the range [L, R][L,R], and assuming \log(R)log(R) is bounded. (In general, the complexity would be O(D\log R)O(DlogR).)
Space Complexity: O(D)O(D), the length of the answer.
划分字母区间
Approach 1: Greedy
Intuition
Let's try to repeatedly choose the smallest left-justified partition. Consider the first label, say it's 'a'. The first partition must include it, and also the last occurrence of 'a'. However, between those two occurrences of 'a', there could be other labels that make the minimum size of this partition bigger. For example, in "abccaddbeffe", the minimum first partition is "abccaddb". This gives us the idea for the algorithm: For each letter encountered, process the last occurrence of that letter, extending the current partition [anchor, j] appropriately.
Algorithm
We need an array last[char] -> index of S where char occurs last. Then, let anchor and j be the start and end of the current partition. If we are at a label that occurs last at some index after j, we'll extend the partition j = last[c]. If we are at the end of the partition (i == j) then we'll append a partition size to our answer, and set the start of our new partition to i+1.
Complexity Analysis
Time Complexity: O(N)O(N), where NN is the length of SS.
Space Complexity: O(1)O(1) to keep data structure last of not more than 26 characters.


每日温度
❌ Solution - I (Brute-Force)
Let's see how we can solve this using brute-force approach.
For each index i, we can just iterate over the array till we either find the the 1st index j such that T[j] > T[i] or reach the end of array.
If we find j such that T[j] > T[i], we have ans[i] = j-i.
Otherwise, ans[i] = 0
Time Complexity : O(N2), where N is the number of elements in the input array T. In the worst case, we iterate till the end of array for each index i. So, the total number of iterations required are N-1 + N-2 + N-3 +...+ 1 = N(N-1)/2 which is equivalent to O(N2)
Space Complexity : O(1), ignoring the space required by the output array
✔️ Solution - II (Decreasing Monotonic Stack)
In the above solution, we can see that in the worst case, we are repeatedly iterating till the end of array either to find the next greater element at the very end or not finding it at all. This is redundant. We can optimize the above approach by observing that multiple elements can share a common warmer day. For eg. Consider [4,3,2,1,5]. In the brute-force, we would have iterated till 5th element in every case and assigned ans[i] as difference between the indices. However, we see that all elments share 5 as the next warmer day.
Thus, the pattern we see is that we iterate forward till we find a warmer day and that day will be the answer for all elements before it that are cooler (and not found a warmer day). Thus, we can maintain a stack consisting of indices of days which haven't found a warmer day. The temperature at these indices will be in decreasing order since we are only storing days that haven't found a warmer next day and hence it is known as decreasing monotonic stack. Whenever we find a current day cur which is warmer, we check elements of stack and assign them the difference of indices for all those elements which have temperature of corresponding day less than T[cur].
Thus, the algorithm can be summarized as -
Initialize an empty stack s and ans array of size N all initialized to 0s.
Iterate over T from the start
For each current day cur, check if today's temperature T[cur] is warmer than values corresponding to previous days' indices stored in stack (T[s.top()]). Assign answer for all elements of stack for whom current day's temperature is warmer (T[cur] > T[s.top()]) and pop them off the stack.
Push cur onto the stack denoting that we need to find warmer next day for cur.
All the elements present in the stack at end don't have a next greater element. We don't have to worry about them since ans is already initialized to 0. Thus, we can directly return ans.
Time Complexity : O(N), In the worst case, we require O(2*N) ~ O(N) iterations.
Space Complexity : O(N), In the worst case, we may have decreasing elements in T and stack will store all N indices in it
✔️ Solution - III (Monotonic Stack - 2)
Another way of modelling the problem in terms of monotonic stack that some may find more intuitive is by starting from the end of the array. We again maintain a monotonic stack in this case as well which is similar to above appraoch, the only change is just that we start from the end.
This will again allow us to find the next warmer element for each index just by looking through the stack. Since we are maintaining a sorted stack (increasing from top-to-bottom), we know that the first element that we find in stack for curth day such that T[s.top()] > T[cur], will be next warmer day required for that element.
In the above image, we start from the end and each time assign next warmer day to be top of stack element. In the 1st approach, we instead started from beginning and only assigned next warmer day/s at once once we find a warmer day than all preciding elements. Both approach should work just fine.
The algorithm can be summarized as -
Initialize an empty stack s and ans array of size N all initialized to 0s.
Iterate over T from the end.
For each current day cur, pop values corresponding from stack that have temperature(T[s.top()]) lower than today's temperature T[cur], i.e, T[s.top()] <= T[cur]. This popping is done because these elements are cooler than T[cur] and occur later on than cur. Thus, they will never be a potential answer for elements on the left.
Now that all elements lower than T[cur] have been popped off, stack s is either empty or has some element warmer than cur.
If stack is empty, assign ans[cur] = 0 because no next warmer element exists for cur.
Otherwise, assign ans[cur] = s.top()-cur, the difference between indices of next warmer element and cur.
Then, Push cur onto the stack since it has potential to be next closest warmer day for remaining elements on left of T.
Finally, return ans.



1比特与2比特字符
Solution Approach:
Traverse the array from 0 to n-2 (leaving the last character).
Now if current char is 0, increment i by 1.
Else increment by 2 as 1 is always followed by either 1 or 0.
After the loop ends check if i is pointing to last char (i.e. n-1) or before that return true, else false.
最短无序连续子数组
Approach 1: Brute Force
Algorithm
In the brute force approach, we consider every possible subarray that can be formed from the given array numsnums. For every subarray nums[i:j]nums[i:j] considered, we need to check whether this is the smallest unsorted subarray or not. Thus, for every such subarray considered, we find out the maximum and minimum values lying in that subarray given by maxmax and minmin respectively.
If the subarrays nums[0:i-1]nums[0:i−1] and nums[j:n-1]nums[j:n−1] are correctly sorted, then only nums[i:j]nums[i:j] could be the required subrray. Further, the elements in nums[0:i-1]nums[0:i−1] all need to be lesser than the minmin for satisfying the required condition. Similarly, all the elements in nums[j:n-1]nums[j:n−1] need to be larger than maxmax. We check for these conditions for every possible ii and jj selected.
Further, we also need to check if nums[0:i-1]nums[0:i−1] and nums[j:n-1]nums[j:n−1] are sorted correctly. If all the above conditions are satisfied, we determine the length of the unsorted subarray as j-ij−i. We do the same process for every subarray chosen and determine the length of the smallest unsorted subarray found.




找到所有数组中消失的数字
❌ Solution - I (Brute-Force)
A brute-force way to solve this question is to take each number in range [1, n] and push it into ans array if it doesn't occur in nums.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
for(int i = 1; i <= size(nums); i++)
if(find(begin(nums), end(nums), i) == end(nums)) // linear search in nums for each i
ans.push_back(i);
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
return [i for i in range(1, len(nums)+1) if i not in nums]
Time Complexity : O(n2), we iterate over the range [1, n] which takes O(n) and for each iteration, we check if that element occurs in nums which takes another O(n) giving total time of O(n2)
Space Complexity : O(1), excluding the space required for the output vector, we only use constant extra space. The output space is generally not included in the space complexity.
✔️ Solution - II (Sort & Binary-Search)
Instead of linear-searching if every element in range [1, n] is present in nums or not, we could instead sort nums and then apply binary-search every time. If the element is not found in nums, we include it in ans.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
sort(begin(nums), end(nums));
vector<int> ans;
for(int i = 1; i <= size(nums); i++)
if(!binary_search(begin(nums), end(nums), i)) // binary search in nums for each i
ans.push_back(i);
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
nums.sort()
return [i for i in range(1, len(nums)+1) if nums[bisect_left(nums, i)%len(nums)] != i]
Time Complexity : O(nlogn), we iterate over the range [1, n] which takes O(n) and for each iteration, we check if that element occurs in nums using binary search which takes another O(logn) giving a total time of O(nlogn)
Space Complexity : O(sort), the only extra space required is the one used in internal sorting algorithm. Ignoring that space, we can say it to be O(1)
✔️ Solution - III (HashSet)
We can do even better if we just insert every element from nums into a hashset and then iterate over the range [1, n] and only add those elements to ans and are not present in hashset.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
unordered_set<int> s(begin(nums), end(nums)); // insert every nums[i] in hashset
vector<int> ans(size(nums) - size(s));
for(int i = 1, j = 0; i <= size(nums); i++)
if(!s.count(i)) ans[j++] = i; // add all elements not found in hashset to ans
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
s = set(nums)
return [i for i in range(1, len(nums)+1) if i not in s]
Time Complexity : O(n), we require O(n) time to insert all elements into hashset and another O(n) time to iterate over range and insert elements not present in hashset into ans, thus giving a total time of O(n).
Space Complexity : O(n), required to maintain the hashset.
✔️ Solution - IV (Boolean array)
We can slightly optimize previous approach by using an boolean array of size n instead of hashset, since the range is known to be [1, n]
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<bool> seen(size(nums)+1);
vector<int> ans;
for(auto c : nums) seen[c] = true;
for(int i = 1; i <= size(nums); i++)
if(!seen[i]) ans.push_back(i);
return ans;
}
};
class Solution:
def findDisappearedNumbers(self, nums):
ans, seen = [], [False]*(len(nums)+1)
for c in nums: seen[c] = True
for i in range(1, len(nums)+1):
if not seen[i]:
ans.append(i)
return ans
Time Complexity : O(n)
Space Complexity : O(n)
✔️ Solution - V (Placing Elements at Correct Index - Space Optimized)
This solution involves placing all possible elements at their right index place. By that, I mean every possible index i should be occupied by correct element i+1, i.e, num[i] = i+1. This allows us to check if a number j from range [1, n] exists in nums or not.
The numbers j will be present in nums only if the number j itself is present at nums[j-1] which is its correct index place.
The numbers j' that are not present in nums wont have correct element (which is j' itself) at its correct index place nums[j'-1].
The numbers j that are not in nums wont have correct element at their right index place (nums[i-1]) and that index place would be occupied by some other element.
Now, Can we do this linearly using constant space? Yes!
We will iterate over each element of nums.
For each element c, if the correct index place of c, i.e, nums[c-1] is not occupied by c, then we place c at its correct index place. But we dont want to lose number which was already present at nums[c-1]. So we swap it instead so the number at nums[c-1] occupies current element c & vice-versa.
We placed original current element c at its correct place but now we have another element as c for which we need to place it at its correct place. So, repeat above step till c is at its correct place in nums.
The steps 2 & 3 are repeated for all elements of nums so that we ensure every possible index is occupied by correct element. At last, the index not occupied by correct element are once which dont occur in nums.
Let nums = [4,3,2,7,8,2,3,1]. The steps take place as -
[7,3,2,4,8,2,3,1]
[3,3,2,4,8,2,7,1]
[2,3,3,4,8,2,7,1]
[3,2,3,4,8,2,7,1]
[3,2,3,4,1,2,7,8]
[1,2,3,4,3,2,7,8]
Index 4 & 5 are not occupied by their correct elements meaning the elements corresponding to those indices are missing

分发饼干
Sort greed array and cookie array. Then simply walk both arrays and match cookie to greed if greed is less than cookie.
找到所有数组中消失的数字
1st for loop: for each value x, negate the element at xth position
2nd for loop: get all the positions that has a positive element. These are the missing values to return.
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
// 1st for loop: nums = [4,3,2,7,8,2,3,1]
for(int i = 0; i < nums.size(); i++) // each iteration:
{ // i = 0 i = 1 i = 2 ... i = 7
int temp = nums[i]; // temp = 4 temp = 3 temp = -2 ... temp = -1
temp = (temp > 0) ? temp : -temp; // temp = 4 temp = 3 temp = 2 ... temp = 1
if(nums[temp-1] > 0) // nums[3] > 0 nums[2] > 0 nums[1] > 0 ... nums[0] > 0
nums[temp-1] *= -1; // [4,3,2,-7,8,2,3,1] [4,3,-2,-7,8,2,3,1] [4,-3,-2,-7,8,2,3,1] ... [-4,-3,-2,-7,8,2,-3,-1]
}
// 2nd for loop: nums = [-4,-3,-2,-7,8,2,-3,-1]
for(int i = 0; i < nums.size(); i++)
if(nums[i] > 0) // the 4th & 5th indexes are positive
ans.push_back(i+1); // ans = [5,6]
return ans;
}

最接近的三数之和
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
//BRUTE FORCE APPROACH...(but a little improved)
//Applying two pointers on the sorted array for target-currnumber
//time complexity O(N^2)
int ans; //...Our Final sum(of all three integers) will be stored here
int prevDiff = INT_MAX; //...this will be the closest difference between target and the sum we calculated...this will be changed each time it is compared with a sum that is found to be lower than the previous closest sum
int temp = target;
sort(nums.begin(),nums.end()); //sorting the array inorder to carry out our two pointer approach
for(int i =0;i<nums.size()-2;i++){ //loop till nums.size()-2 because we always play with three pointers two of which we don't want to get out of the array
temp = target-nums[i]; //reducing the target to target-curr value(this curr value is one of the three integers we take into consideration)
int start = i+1; // starting from one index ahead of curr index
int end = nums.size()-1;
int x; // for calculating and comparing with the new target value(temp)...this is similar as two sum problem..
// so the idea here is to get the sum of two integers as closest as (or equal to ) the new target(temp) which is done by
// keeping two pointers and changing their positions so as to get as close as possible to our new target value.
while(start<end){
x = nums[start]+nums[end];
if(x==temp) break; //breaking here ... cuz can't get any closer than the TARGET ITSELF!
if(x<temp) start++; //incase the sum is lower we shift start to right side so as to increase sum and get closer to our target value(temp)
else end--;
}
//now here after this traversal we have obtained a value of sum of three integers as close to temp as possible
//this value is x + nums[i]
//we take the difference of target value (original) with this sum and compare this difference with previous difference(because we need to be as close to target as possible right!)
//if difference is less than prev diff we update our ans and prevDifference gets equal to this difference value..
if(abs(target-(x+nums[i]))<prevDiff){
ans = x+nums[i];
prevDiff = abs(target-(x+nums[i]));
}
}
return ans; //hooray!
}
};


四数相加||
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
int count=0;
unordered_map<int,int> mp;
/* Philosophy
1. I know that Addtion have two parts in it EG (a +b , Part 1 - a, Part 2- b.
2.So, Lets make and find this dependency factors. How can I do it?
3. If there are 4 Sum. it means 2 sums is going to Part 1 and another 2 gonna be Part 2 which are dependent on Part 1 for 0 resultant.
4. I gonna store summation 2 nums1 in a FREQUENCY Hashmap.
5. Then I traverse 2nd part of the summation (rest to nums) and keep checking that do (0-it1-it2) is exist in map .
6. If yes, the add the frequency of Part1 int COUNT var.
7. return count;
*/
//Traversing Part 1
for (auto &it1: nums1)
for (auto &it2:nums2)
mp[it1+it2]++;
// Traversing Part 2
for(auto &it3: nums3)
for(auto &it4:nums4)
if(mp.count(0-it3-it4)) count+=mp[0-it3-it4];
return count;
}
};

分治:最长公共前缀
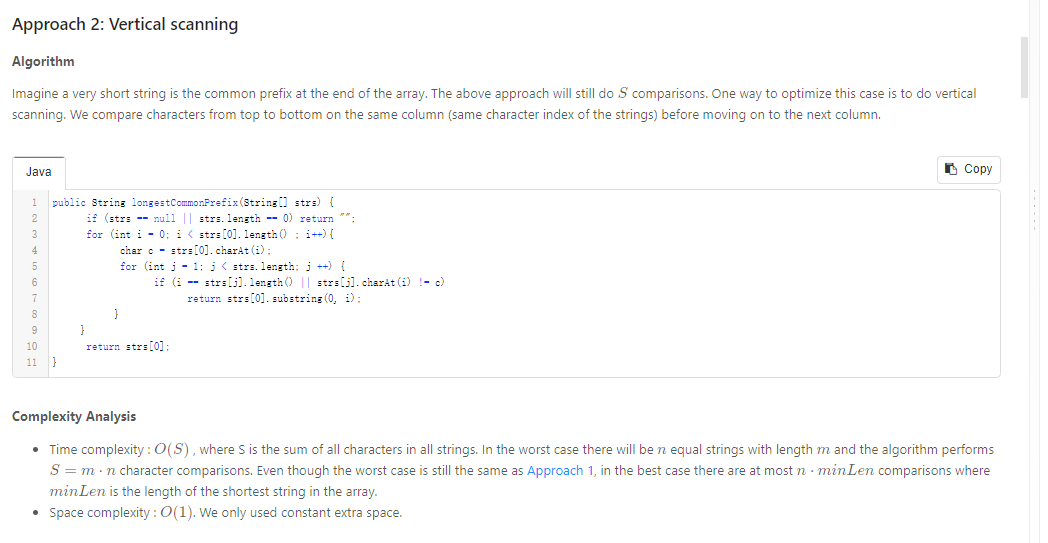



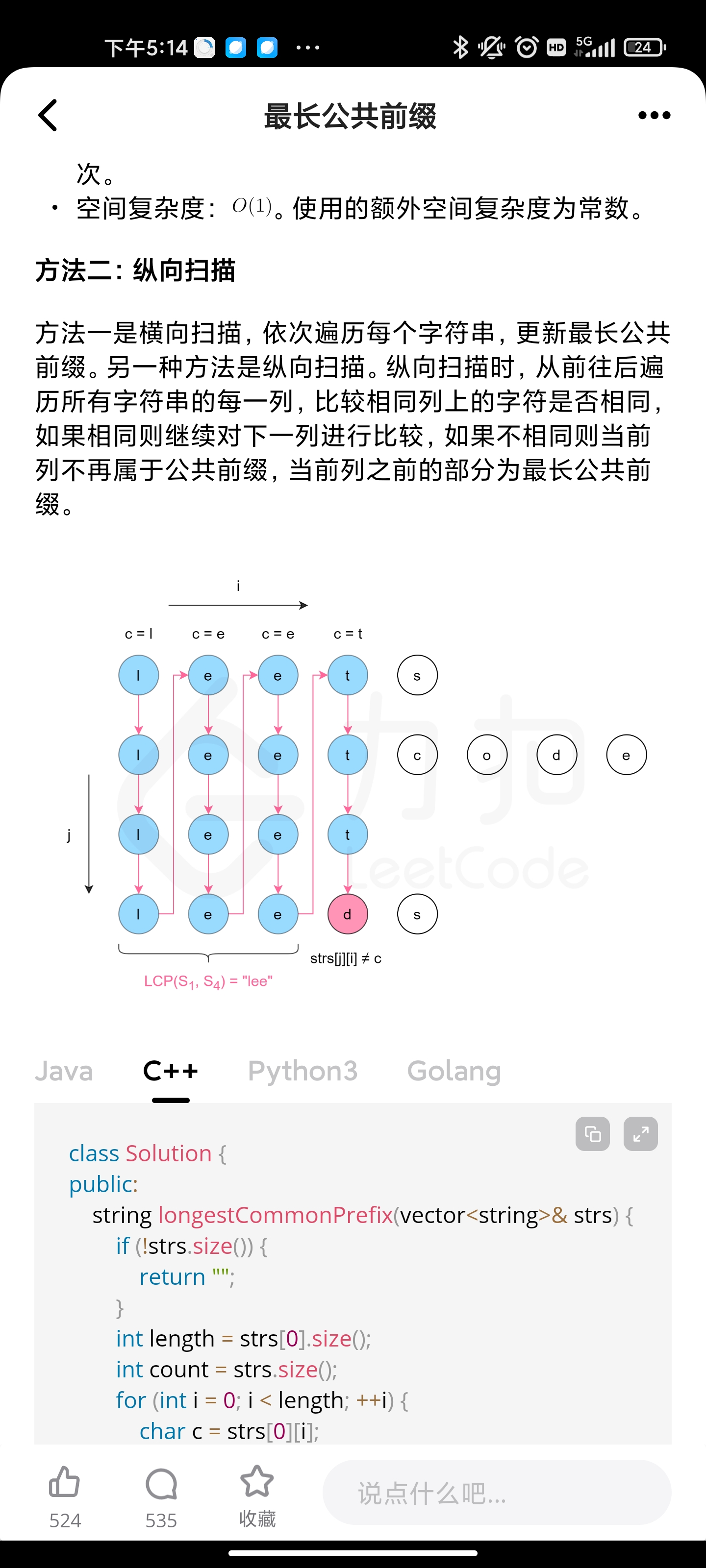
整数反转
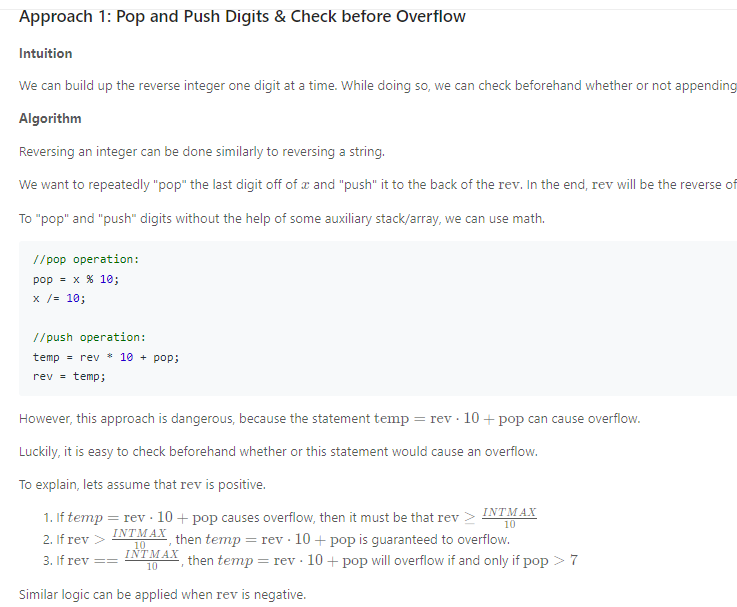


盛水最多的容器
Explanation :
Intuition : Volume/Area depends upon the bar having minimum height
Now suppose, height[i] < height[j], in this case we can only store water with area height[i]*(j-i), now there is chance there is a greater value of i present in array so increment i
Vice-vera height[i]>height[j], here area would be height[j]*(j-i), in this case there's chance a greater value of j is present in array so decrement j
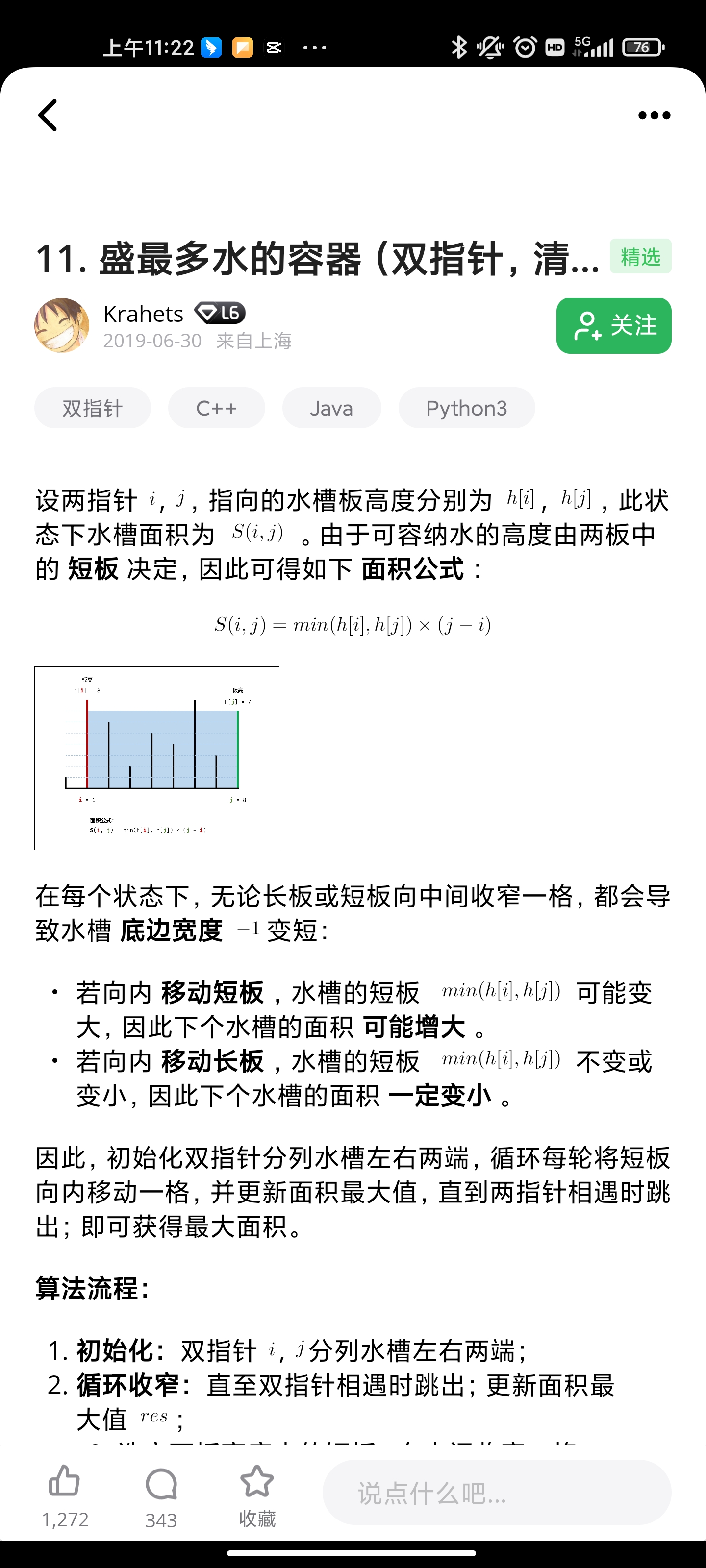
无重复字符的最长子串
A solution for beginners, which is straightforward, easy to understand, without too many complications and room to optimize once you understand the basic premise of the question. Hope this helps!
Time Complexity: O(n)
Space Complexity: O(min of a,b) for the unordered set. a, is the upper bound of the space complexity.
Where a: Size of the string
b: Size of the number of characters in the character-set