二叉平衡树（C++）

news2024/9/27 19:23:18

背景：

  二叉平衡树，就是根据二叉搜索树进行优化，让其速度更加的快，如果读者没有学过二叉搜索树，可以前往以下链接查看资料：
http://t.csdn.cn/cCDQDhttp://t.csdn.cn/cCDQD

二叉搜索树的缺陷：

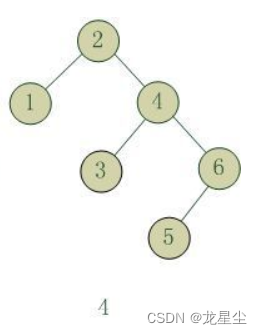
   在以上链接中，我们讲解了二叉搜索树：就是一个二叉树，有着特殊的性质，搜索时间很快！但是这有着一个致命的缺陷，我们给出一个例子，假设我们输入1,2,3,4,5,6,组成的二叉搜索树是这样的：

1.1 和数组搜索时间一样的二叉搜索树

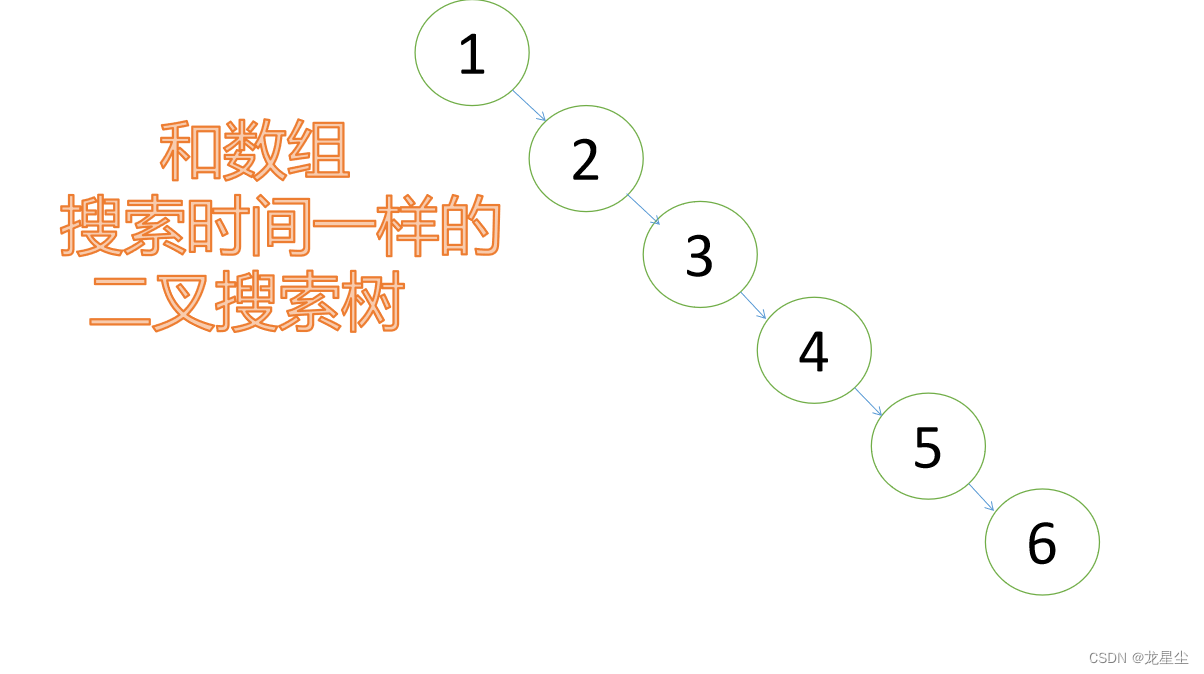
  这样的二叉搜索树，不就和普通的数组查找时间一样吗？连二分查找都不如，会浪费二叉树的大把空间，我们再看一个例子，输入6,5,4,3,2,1的二叉搜索树是这样的：

1.2 以递减序输入造成的二叉搜索树​​​​​​

   以上这个二叉搜索树是根据输入的递减序来进行创建的，而图1.1则是通过递增序输入而造成的二叉搜索树，所以我们知道，如果我们的输入是递增、递减序的话，那么组成的二叉搜索树的搜索时间就和数组一样的。

  所以我们要进行优化，怎么优化呢？就是在二叉搜索树的基础上优化出一个AVL数（二叉平衡树）来。

二叉平衡树简介：

  平衡二叉树也叫做AVL树,AVL树的名字来源于它的发明作者G.M. Adelson-Velsky 和 E.M. Landis。AVL树是最先发明的自平衡二叉查找树(Self-Balancing Binary Search Tree,简称平衡二叉树。

  我们怎么知道这棵二叉搜索树平不平衡呢？我们知道，二叉搜索树的搜索时间和高度是有直接关系的，但是我们按递增、递减序输入之后，高度就和n一样了，所以时间复杂度为O(log n).想要优化，就是改变这棵二叉搜索树的高度。

  首先，我们就是要知道，怎么样才要改变二叉搜索树的高度，难道只是递增、递减序的输入吗？不是的，只要左子树高度与右子树高度没有高度平衡的话，我们就需要进行一次改变二叉搜索树高度的操作。

  什么叫高度平衡呢？就是两者高度相减的绝对值（abs函数可以求解）c，如果c不等于0（高度一样），不等于1，不等于-1（等于1和-1都是两者相差1），那么说明次二叉搜索树不是高度平衡，反之，这棵二叉搜索树就是高度平衡。

  假设呢？我们输入1,2,3来组建二叉搜索树：  

2.1 输入1,2,3后组成的二叉搜索树

 

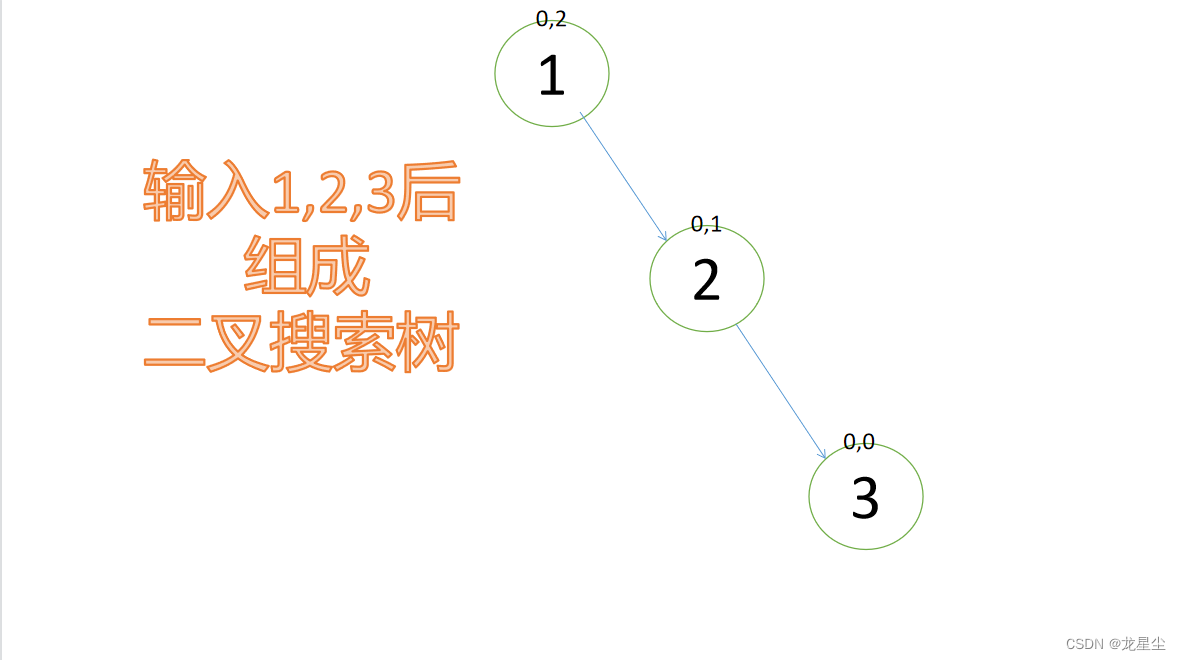
  每一个节点上方都有两个数字，左边的代表其左子树的高度，右边的代表其右子树的高度，从根节点开始，右子树减左子树的绝对值为2，不是-1,0,1，所以这不是一颗高度平衡的树，那么怎么样才是高度平衡的树呢？

  以下为输入1,2,3后组成的一颗高度平衡的树（平衡二叉树）：

2.2 输入1,2,3组成的高度平衡的二叉搜索树（二叉平衡树）

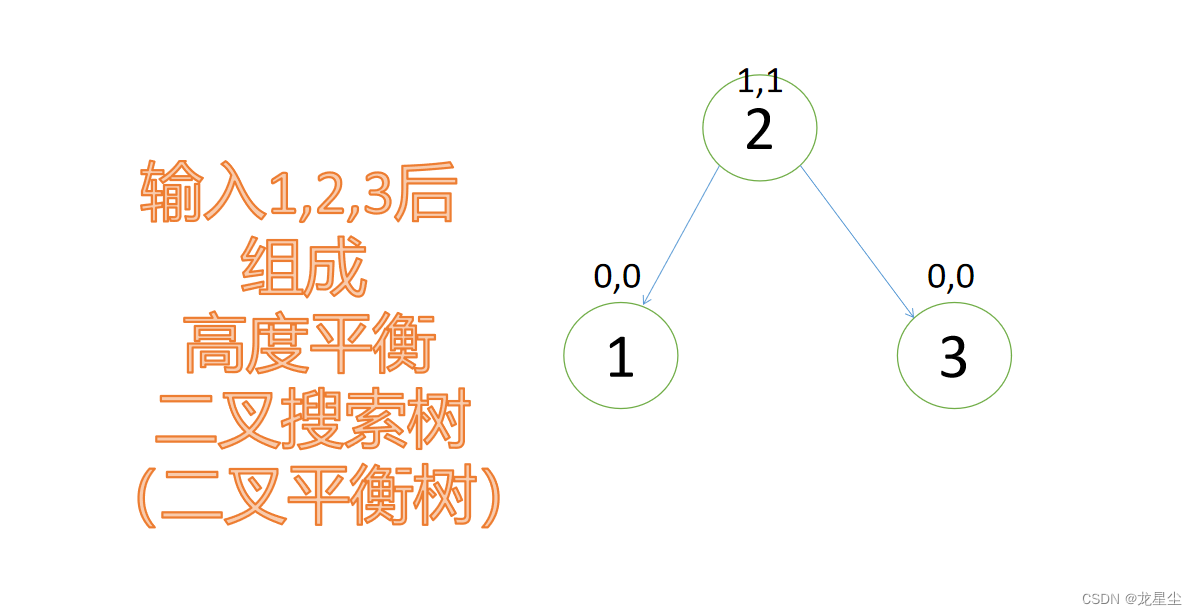
     以上就是一颗二叉平衡树，这样我们查找的最长时间为O(2),之前那棵不平衡的二叉搜索树却需要O(3)的时间，别看差距只有O(1)，如果数据大了之后，差距可是非常的大的。

初始结构代码：

struct Node{
	int data;
	int r_high;
	int l_high;
	int high;
	Node* lchild;
	Node* rchild;
};

如何进行平衡操作：

  思路1（调整输入顺序）：

  看我们上面的图，输入1,2,3后组成了一颗不平衡的二叉搜索树，但是如果我们输入2,1,3那么就可以解决这个问题，可以创建出高度平衡的二叉搜索树。

  这个方法行不行呢？肯定是不行的呀，兄弟们啊！我们讲的是动态搜索啊，什么是动态啊，就是你在进行插入删除操作的之后，依旧可以进行查找，我们永远不知道输入来的下一个数是什么？更不能提前挑好输入顺序了呀，这个方法是不符合实际的，所以不能采用。

  思路2（盯好BF）：

  我们这个思路就是要做好“盯好BF”，BF是什么呢？大家不要误解了啊，BF并不是男朋友的缩写哈，在计算机编程之中，BF就是每一个结点的高度，就是要我们盯紧这个二叉搜索树是不是高度平衡，如果是，那么不用管，如果不是，那么需要进行平衡操作，使其依旧保持高度平衡（并且符合二叉搜索树的基本性质：左子节点小于根节点，右子节点大于根节点）。

  我们怎么求每一个节点的高度呢？我们可以编写一个函数来解决，就是一个递归还是，不断的前往其的左子节点、右子节点，如果不为空的话那么进行计数器倒推++，这样就可以求出左子树的高度和右子树的高度，对两者相减的绝对值进行判断，是不是高度平衡。

  我们可以进行一次总结，看看二叉搜索树有哪些不平衡的的情形。

平衡二叉树不平衡的情形：

把需要重新平衡的结点叫做q，由于任意两个结点最多只有两个儿子，因此高度不平衡时，α结点的两颗子树的高度相差2.容易看出，这种不平衡可能出现在下面4中情况中：

1.对q的左儿子的左子树进行一次插入

2.对q的左儿子的右子树进行一次插入

 

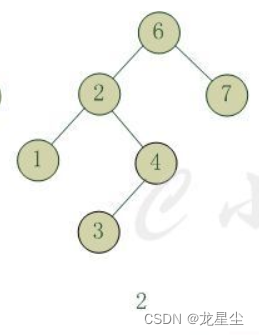
3.对q的右儿子的左子树进行一次插入

 

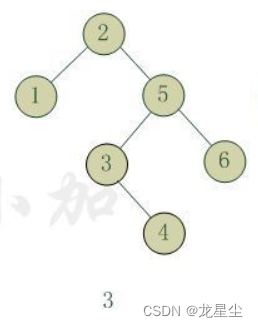
4.对q的右儿子的右子树进行一次插入

 

  情形1和情形4是关于q的镜像对称(也就是说在情形1在镜子里的样子就是情形4），二情形2和情形3(也就是说在情形2在镜子里的样子就是情形3）也是关于q的镜像对称，因此理论上看只有两种情况，但编程的角度看还是四种情形。

  第一种情况是插入发生在“外边”的情形（左左或右右），该情况可以通过一次单旋转完成调整；第二种情况是插入发生在“内部”的情形（左右或右左），这种情况比较复杂，需要通过双旋转来调整。

调整措施：

一、单旋转

左左情况的二叉搜索树

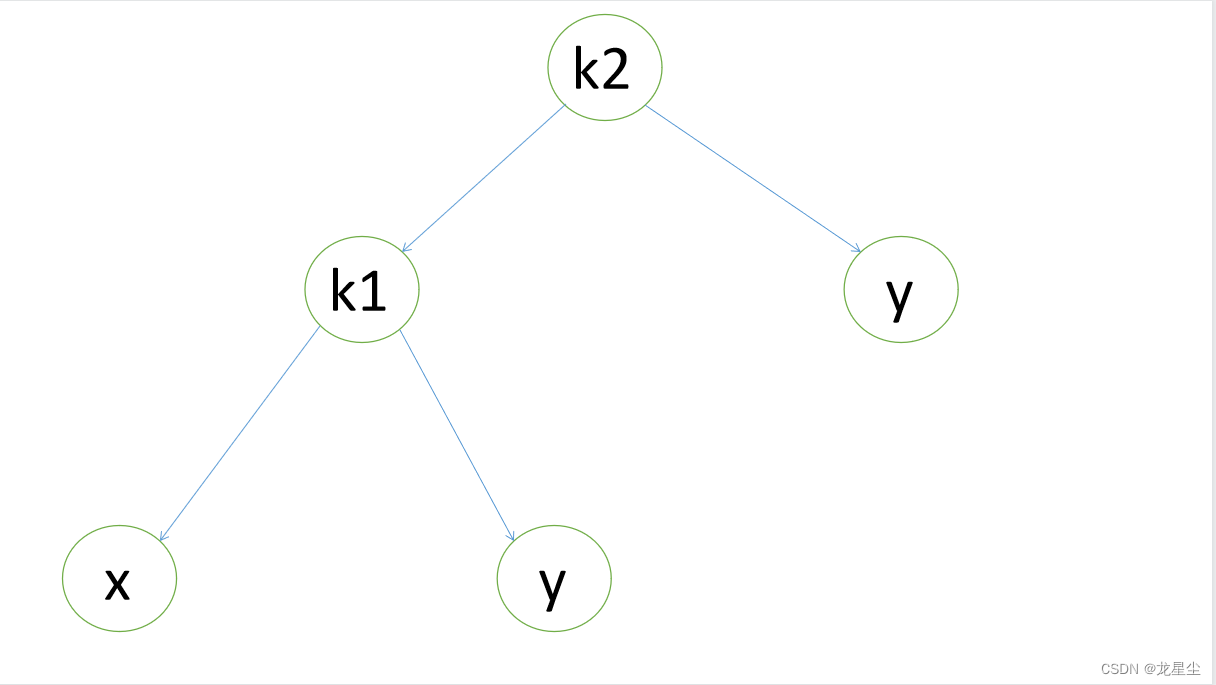
   也就是从根节点k2开始，左子节点有两个结点，并且没有高度平衡，这样我们可以进行一次单旋的操作。

进行一次单旋过后的二叉搜索树

 

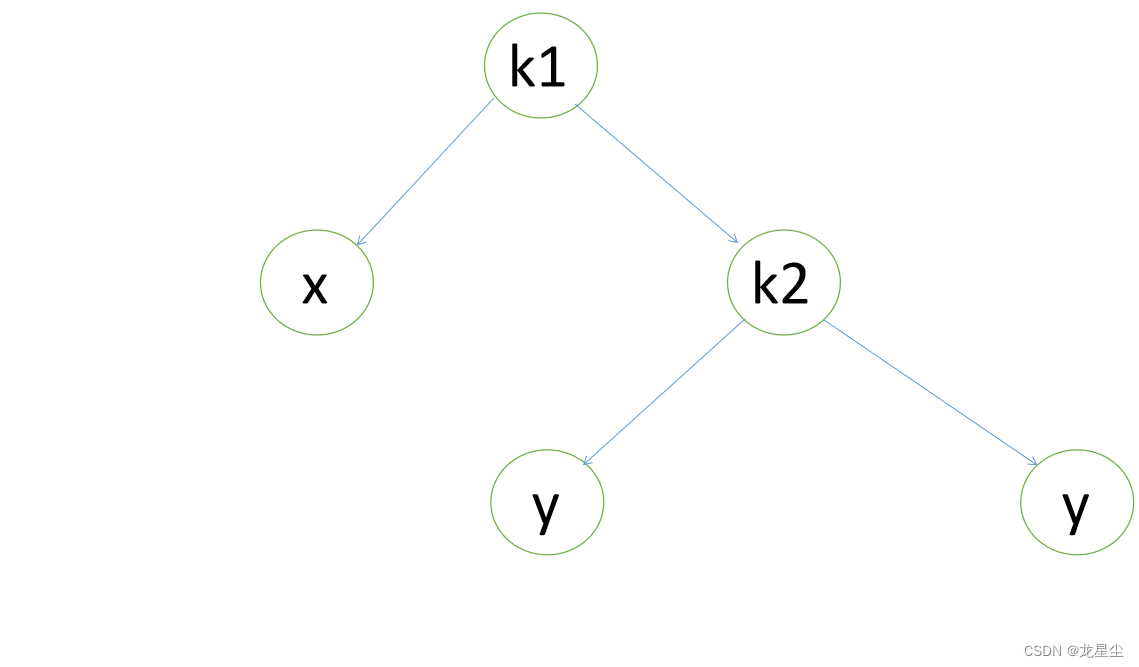
  上图是左左的情况，k2结点不满足平衡性，它的左子树k1比右子树z深两层，k1子树中更深的是k1的左子树x，因此属于左左情况。

  为了恢复平衡，我们把x上移一层，并把z下移一层，但此时实际已经超出了AVL树的性质要求。为此，重新安排结点以形成一颗等价的树。为使树恢复平衡，我们把k2变成这棵树的根节点，因为k2大于k1，把k2置于k1的右子树上，而原本在k1右子树的Y大于k1，小于k2，就把Y置于k2的左子树上，这样既满足了二叉查找树的性质，又满足了平衡二叉树的性质。

这种情况称为单旋转。

二、双旋转

对于左右和右左两种情况，单旋转不能解决问题，要经过两次旋转。

我们以左右来作为例子：

左右情况的二叉搜索树

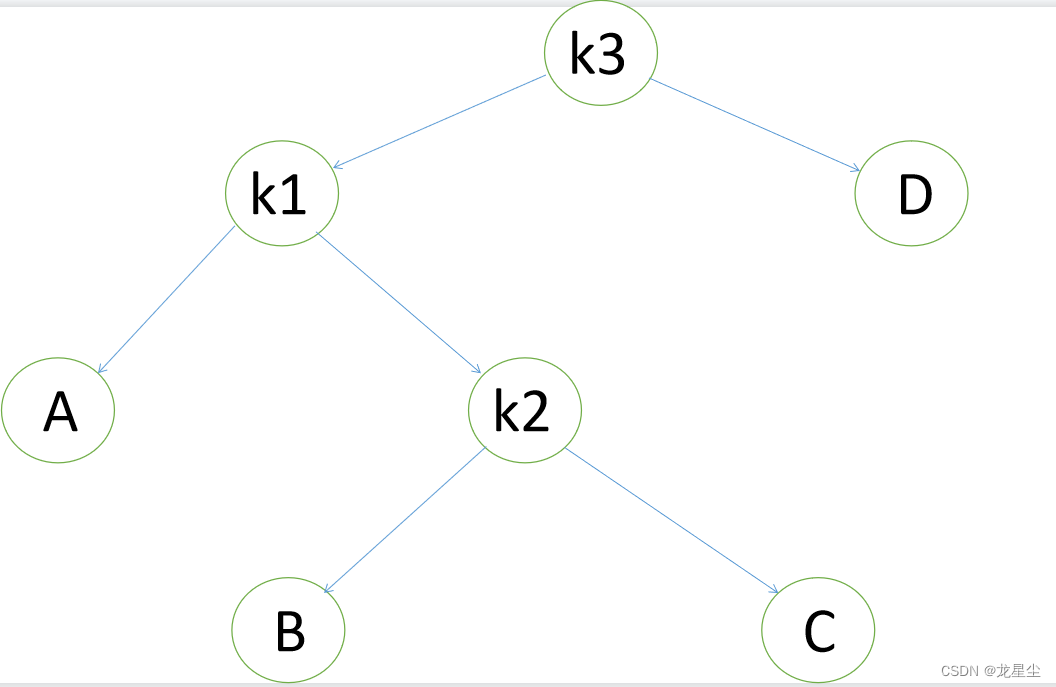
   这种情况，进行一次单旋过后，依旧不是高度平衡，所以我们需要再次进行一次单旋操作，俗称双旋！

  以下为第一次单旋过后的图：

进行了一次单旋的二叉搜索树

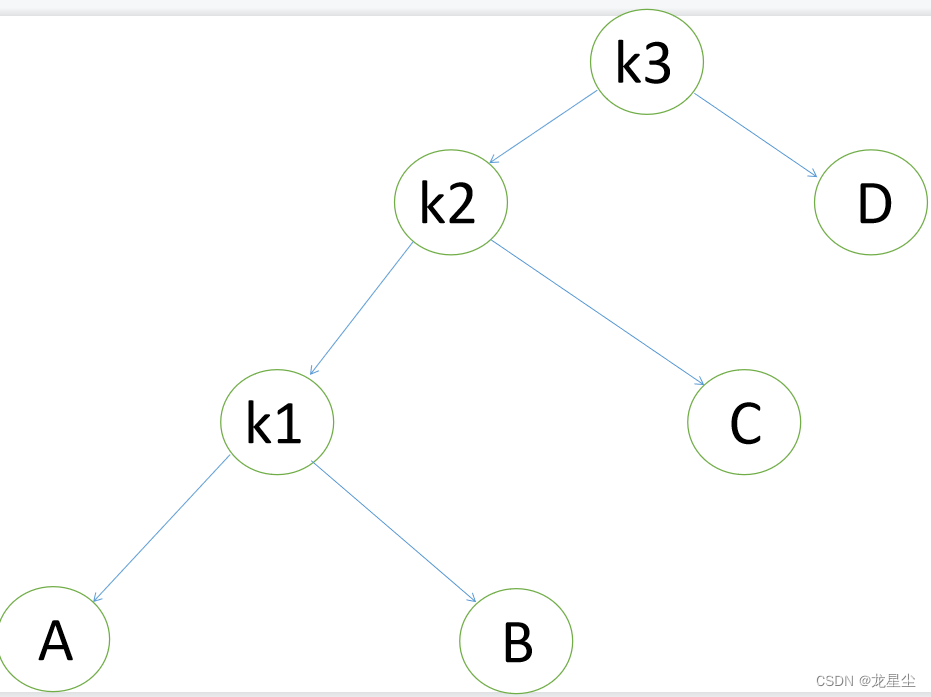
   第二次双旋过后的图：

双旋结束过后的二叉搜索树

 对于上图情况，为使树恢复平衡，我们需要进行两步，第一步，把k1作为根，进行一次右右旋转，旋转之后就变成了左左情况，所以第二步再进行一次左左旋转，最后得到了一棵以k2为根的平衡二叉树。

代码：

bool cz=false;
bool sx=false;
bool CZ=false;
void AVL_CZ(Node* &q,Node *c){
	if(CZ)
	  return ;
	if(q==NULL){
		q=c;
		CZ=true;
		return ;
	}
	bool f=cmp(c->data,q->data);
	if(f)
	  AVL_CZ(q->rchild,c);
	else
	  AVL_CZ(q->lchild,c);
}
void AVL_TC(Node* &q){
	if(cz)
	  return ;
	int c=abs(q->l_high-q->r_high);
	if(!(c!=1&&c!=0&&c!=-1)){
		cz=true;
		return ;
	}
	if(q->l_high>q->r_high){
		AVL_TC(q->lchild);
		if(cz==true&&sx==false){
			Node *p=q;
			q=q->lchild;
			p->lchild=NULL;
			sx=true;
			if(q->rchild==NULL)
			  q->rchild=p;
			else{
				Node *c;
				c=q->rchild;
				q->rchild=p;
				AVL_CZ(q,c);
			}
		}
	}
	else{
		AVL_TC(q->rchild);
		if(cz==true&&sx==false){
			Node *p=q;
			q=q->rchild;
			p->rchild=NULL;
			sx=true;
			if(q->lchild==NULL)
			  q->lchild=p;
			else{
				Node *c;
				c=q->lchild;
				q->lchild=p;
				AVL_CZ(q,c);
			}
		}
	}
}
void AVL(Node* &x){
	int c=abs(x->l_high-x->r_high);
	if(c!=1&&c!=0&&c!=-1){
		cz=sx=CZ=false;
		AVL_TC(x);
	}
}

二叉平衡树的初始化函数：

void init(Node* &p){
	p=new Node; 
	p->l_high=p->r_high=p->high=0;
	p->data=-1;
	p->lchild=new Node;
	p->rchild=new Node;
	p->lchild=NULL;
	p->rchild=NULL;
}
//将高进行调整
void init2(Node *q){
	q->l_high--,q->r_high--,q->high=max(q->l_high,q->r_high);
	if(q->lchild==NULL&&q->rchild==NULL)
	  return ;
	if(q->lchild!=NULL)
	  init2(q->lchild);
	if(q->rchild!=NULL)
	  init2(q->rchild);
}

二叉平衡树的求左右子树高度函数：

  之前我们讲了，可以运用递归的形式，倒退加法！

求高度函数：

int high(Node* &q){
	q->l_high=q->r_high=q->high=1;
	if(q->lchild==NULL&&q->rchild==NULL)
	  return 1;
	if(q->lchild!=NULL)
	  q->l_high+=high(q->lchild);
	if(q->rchild!=NULL)
	  q->r_high+=high(q->rchild);
	q->high=max(q->l_high,q->r_high);
	return q->high;
}

二叉平衡树的查找操作：

  这个很简单，就和二叉搜索树一样，

  我们可以应用递归的形式,如果q->lf为真，并且用cmp(q->data,s)进行比较之后，递归去q->lchild看看，如果q->rf为真，递归去q->rchild看看，每次到一个节点，都要比较这个结点和s是不是一样（pd函数），如果一样，返回为真。

查找函数代码：

bool S=false;
void search(Node *q,int s){
	if(S)
	  return ;
	if(q->data==s){
		S=true;
		return ;
	}
	if(q->lchild==NULL&&q->rchild==NULL)
	  return ;
	bool f=cmp(q->data,s);
	if(f)
	  search(q->lchild,s);
	else
	  search(q->rchild,s);
}

二叉平衡树的删除操作：

  我们以上已经将二叉搜索树优化成了二叉平衡树，接下来我们需要进行二叉平衡树的删除操作！

同插入操作一样，删除结点时也有可能破坏平衡性，这就要求我们删除的时候要进行平衡性调整。

删除分为以下几种情况：

首先在整个二叉树中搜索要删除的结点，如果没搜索到直接返回不作处理，否则执行以下操作：

1.要删除的节点是当前根节点T。

如果左右子树都非空。在高度较大的子树中实施删除操作。

分两种情况：

(1)、左子树高度大于右子树高度，将左子树中最大的那个元素赋给当前根节点，然后删除左子树中元素值最大的那个节点。

(1)、左子树高度小于右子树高度，将右子树中最小的那个元素赋给当前根节点，然后删除右子树中元素值最小的那个节点。

如果左右子树中有一个为空，那么直接用那个非空子树或者是NULL替换当前根节点即可。

2、要删除的节点元素值小于当前根节点T值，在左子树中进行删除。

递归调用，在左子树中实施删除。

这个是需要判断当前根节点是否仍然满足平衡条件，

如果满足平衡条件，只需要更新当前根节点T的高度信息。

否则，需要进行旋转调整：

如果T的左子节点的左子树的高度大于T的左子节点的右子树的高度，进行相应的单旋转。否则进行双旋转。

3、要删除的节点元素值大于当前根节点T值，在右子树中进行删除。

删除函数代码：

bool SC=false;
Node* TH=NULL;
void AVL_remove(Node* &q,int s){
	if(SC)
	  return ;
	if(q->data==s){
		Node *a=q;
		if(q->lchild==NULL&&q->rchild==NULL)
		  q=NULL;
		else if(a->l_high>=a->r_high&&q->lchild!=NULL&&((q->lchild->lchild==NULL||q->lchild->rchild==NULL)&&q->lchild->lchild!=q->lchild->rchild)){
			q=q->lchild;
			if(a->rchild!=NULL)
			  q->rchild=a->rchild;
		}
		else if(a->l_high<=a->r_high&&q->rchild!=NULL&&((q->rchild->lchild==NULL||q->rchild->rchild==NULL)&&q->rchild->lchild!=q->rchild->rchild)){
			q=q->rchild;
			if(a->lchild!=NULL)
			  q->lchild=a->lchild;
		}
		SC=true;
		return ;
	}
	bool f=cmp(q->data,s);
	if(f)
	  AVL_remove(q->lchild,s);
	else
	  AVL_remove(q->rchild,s);
}
bool remove(Node* &q,int s){
	search(q,s);
	if(S){
		AVL_remove(q,s);
		if(SC)
		  return true;
		else
		  return false;
	}
	else
	  return false;
}

main主函数代码:

int main(){
	Node* p;
	init(p); 
	while(1){
		cout<<"1.插入\n2.查找\n3.删除\n";
		int c;
		cin>>c;
		if(c==1){
			int a;
			cout<<"输入要插入的数:";
			cin>>a;
			bool f=insert(p,a);
			if(!f){
				cout<<"插入失败！\n";
				return 0;
			}
			high(p);
			AVL(p); 
			high(p);
			init2(p);
			puts("树:");
			print(p);
		}
		else if(c==2){
			int a;
			cout<<"输入要查找的数:";
			cin>>a;
			S=false;
			search(p,a);
			if(S)
			  cout<<"在二叉伸展树中有这个数!\n";
			else
			  cout<<"没有查到此数!\n";
		}
		else if(c==3){
			int a;
			cout<<"请输入你要删除的数:";
			cin>>a;
			S=SC=false;
			TH=NULL;
			bool f=remove(p,a);
			if(f){
				cout<<"删除成功!\n";
				high(p);
				AVL(p); 
				high(p);
				init2(p);
				puts("树:");
				print(p);
			}
			else
			  cout<<"删除失败,没有这个数!\n";
		}
		else
		  cout<<"重新输入!\n";
		puts(" ");
	}
	return 0;
}

全部代码：

#include<bits/stdc++.h>
using namespace std;
int n;
struct Node{
	int data;
	int r_high;
	int l_high;
	int high;
	Node* lchild;
	Node* rchild;
};
void init(Node* &p){
	p=new Node; 
	p->l_high=p->r_high=p->high=0;
	p->data=-1;
	p->lchild=new Node;
	p->rchild=new Node;
	p->lchild=NULL;
	p->rchild=NULL;
}
bool cmp(int a,int b){
	return a>b;
}
bool insert(Node *q,int s){
	while(1){
		if(q->lchild==NULL&&q->rchild==NULL&&q->data==-1){
			q->data=s;
			return true;
		}
		bool f=cmp(q->data,s);
		if(f){
			if(q->lchild==NULL)
			  init(q->lchild);
			q=q->lchild;
		}
		else{
			if(q->rchild==NULL)
			  init(q->rchild);
			q=q->rchild;
		}
	}
	return false;
}
void print(Node* q,int a=-1,int b=-1){
	if(a==-1)
	  cout<<"根节点:";
	else{
		if(b==1)
		  cout<<a<<"的左子节点:";
		else
		  cout<<a<<"的右子节点:";
	}
	cout<<q->data<<endl<<"  左子树高:"<<q->l_high<<endl<<"  右子树高:"<<q->r_high<<endl;
	if(q->lchild==NULL&&q->rchild==NULL)
	  return ;
	if(q->lchild!=NULL)
	  print(q->lchild,q->data,1);
	if(q->rchild!=NULL)
	  print(q->rchild,q->data,2);
}
void init2(Node *q){
	q->l_high--,q->r_high--,q->high=max(q->l_high,q->r_high);
	if(q->lchild==NULL&&q->rchild==NULL)
	  return ;
	if(q->lchild!=NULL)
	  init2(q->lchild);
	if(q->rchild!=NULL)
	  init2(q->rchild);
}
int high(Node* &q){
	q->l_high=q->r_high=q->high=1;
	if(q->lchild==NULL&&q->rchild==NULL)
	  return 1;
	if(q->lchild!=NULL)
	  q->l_high+=high(q->lchild);
	if(q->rchild!=NULL)
	  q->r_high+=high(q->rchild);
	q->high=max(q->l_high,q->r_high);
	return q->high;
}
bool cz=false;
bool sx=false;
bool CZ=false;
void AVL_CZ(Node* &q,Node *c){
	if(CZ)
	  return ;
	if(q==NULL){
		q=c;
		CZ=true;
		return ;
	}
	bool f=cmp(c->data,q->data);
	if(f)
	  AVL_CZ(q->rchild,c);
	else
	  AVL_CZ(q->lchild,c);
}
void AVL_TC(Node* &q){
	if(cz)
	  return ;
	int c=abs(q->l_high-q->r_high);
	if(!(c!=1&&c!=0&&c!=-1)){
		cz=true;
		return ;
	}
	if(q->l_high>q->r_high){
		AVL_TC(q->lchild);
		if(cz==true&&sx==false){
			Node *p=q;
			q=q->lchild;
			p->lchild=NULL;
			sx=true;
			if(q->rchild==NULL)
			  q->rchild=p;
			else{
				Node *c;
				c=q->rchild;
				q->rchild=p;
				AVL_CZ(q,c);
			}
		}
	}
	else{
		AVL_TC(q->rchild);
		if(cz==true&&sx==false){
			Node *p=q;
			q=q->rchild;
			p->rchild=NULL;
			sx=true;
			if(q->lchild==NULL)
			  q->lchild=p;
			else{
				Node *c;
				c=q->lchild;
				q->lchild=p;
				AVL_CZ(q,c);
			}
		}
	}
}
void AVL(Node* &x){
	int c=abs(x->l_high-x->r_high);
	if(c!=1&&c!=0&&c!=-1){
		cz=sx=CZ=false;
		AVL_TC(x);
	}
}
bool S=false;
void search(Node *q,int s){
	if(S)
	  return ;
	if(q->data==s){
		S=true;
		return ;
	}
	if(q->lchild==NULL&&q->rchild==NULL)
	  return ;
	bool f=cmp(q->data,s);
	if(f)
	  search(q->lchild,s);
	else
	  search(q->rchild,s);
}
bool SC=false;
Node* TH=NULL;
void AVL_remove(Node* &q,int s){
	if(SC)
	  return ;
	if(q->data==s){
		Node *a=q;
		if(q->lchild==NULL&&q->rchild==NULL)
		  q=NULL;
		else if(a->l_high>=a->r_high&&q->lchild!=NULL&&((q->lchild->lchild==NULL||q->lchild->rchild==NULL)&&q->lchild->lchild!=q->lchild->rchild)){
			q=q->lchild;
			if(a->rchild!=NULL)
			  q->rchild=a->rchild;
		}
		else if(a->l_high<=a->r_high&&q->rchild!=NULL&&((q->rchild->lchild==NULL||q->rchild->rchild==NULL)&&q->rchild->lchild!=q->rchild->rchild)){
			q=q->rchild;
			if(a->lchild!=NULL)
			  q->lchild=a->lchild;
		}
		SC=true;
		return ;
	}
	bool f=cmp(q->data,s);
	if(f)
	  AVL_remove(q->lchild,s);
	else
	  AVL_remove(q->rchild,s);
}
bool remove(Node* &q,int s){
	search(q,s);
	if(S){
		AVL_remove(q,s);
		if(SC)
		  return true;
		else
		  return false;
	}
	else
	  return false;
}
int main(){
	Node* p;
	init(p); 
	while(1){
		cout<<"1.插入\n2.查找\n3.删除\n";
		int c;
		cin>>c;
		if(c==1){
			int a;
			cout<<"输入要插入的数:";
			cin>>a;
			bool f=insert(p,a);
			if(!f){
				cout<<"插入失败！\n";
				return 0;
			}
			high(p);
			AVL(p); 
			high(p);
			init2(p);
			puts("树:");
			print(p);
		}
		else if(c==2){
			int a;
			cout<<"输入要查找的数:";
			cin>>a;
			S=false;
			search(p,a);
			if(S)
			  cout<<"在二叉伸展树中有这个数!\n";
			else
			  cout<<"没有查到此数!\n";
		}
		else if(c==3){
			int a;
			cout<<"请输入你要删除的数:";
			cin>>a;
			S=SC=false;
			TH=NULL;
			bool f=remove(p,a);
			if(f){
				cout<<"删除成功!\n";
				high(p);
				AVL(p); 
				high(p);
				init2(p);
				puts("树:");
				print(p);
			}
			else
			  cout<<"删除失败,没有这个数!\n";
		}
		else
		  cout<<"重新输入!\n";
		puts(" ");
	}
	return 0;
}

样例：

输入样例:

1
1
1
2
1
3
2
1
3
1

输出样例:

1.插入
2.查找
3.删除
1
输入要插入的数:1
树:
根节点:1
  左子树高:0
  右子树高:0

1.插入
2.查找
3.删除
1
输入要插入的数:2
树:
根节点:1
  左子树高:0
  右子树高:1
1的右子节点:2
  左子树高:0
  右子树高:0

1.插入
2.查找
3.删除
1
输入要插入的数:3
树:
根节点:2
  左子树高:1
  右子树高:1
2的左子节点:1
  左子树高:0
  右子树高:0
2的右子节点:3
  左子树高:0
  右子树高:0

1.插入
2.查找
3.删除
2
输入要查找的数:1
在二叉伸展树中有这个数!

1.插入
2.查找
3.删除
3
请输入你要删除的数:1
删除成功!
树:
根节点:2
  左子树高:0
  右子树高:1
2的右子节点:3
  左子树高:0
  右子树高:0

总结：

对于二叉平衡树来说，速度还是非常的快的，但是还有一项可以继续的优化，这一点可以看我的下一个文章“二叉伸展树”。 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/371581.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Spark分布式内存计算框架——Spark Streaming】1. Streaming 概述（上）Streaming 应用场景、Lambda 架构

【Spark分布式内存计算框架——Spark Streaming】1. Streaming 概述（上）Streaming 应用场景、Lambda 架构

前言 在很多实时数据处理的场景中&#xff0c;都需要用到流式处理&#xff08;Stream Process&#xff09;框架&#xff0c;Spark也包含了两个完整的流式处理框架Spark Streaming和Structured Streaming&#xff08;Spark 2.0出现&#xff09;&#xff0c;先阐述流式处理框架&…
阅读更多...
Linux--TCP编程--0216 17

Linux--TCP编程--0216 17

观前提示&#xff1a;本篇博文的一些接口需要前几篇博文实现的 线程池的实现Liunx--线程池的实现--0208 09_Gosolo&#xff01;的博客-CSDN博客 线程池的单例模式Linux--线程安全的单例模式--自旋锁--0211_Gosolo&#xff01;的博客-CSDN博客 1.TCP编程需要用的接口 创建 sock…
阅读更多...
【数据挖掘】EDA——以2022雪浪算力开发者大赛数据为例

【数据挖掘】EDA——以2022雪浪算力开发者大赛数据为例

作者简介&#xff1a;重庆大学22级研一&#xff0c;研究方向&#xff1a;时空数据挖掘、图神经网络。目前正在学习大数据、数据挖掘等相关知识&#xff0c;希望毕业后能找到数据相关岗位。 前言 之前写了一个比赛复盘&#xff08;【竞赛复盘】2022雪浪算力开发者大赛——阀体异…
阅读更多...
Python脚本之准备测试环境的用户数据

Python脚本之准备测试环境的用户数据

本文为博主原创&#xff0c;未经授权&#xff0c;严禁转载及使用。 本文链接&#xff1a;https://blog.csdn.net/zyooooxie/article/details/127645678 这期是讲述下 我准备测试环境用户数据的经历。 【实际这篇博客推迟发布N个月】 个人博客&#xff1a;https://blog.csdn.…
阅读更多...
【读书笔记】《深入浅出数据分析》第三章 寻找最大值

【读书笔记】《深入浅出数据分析》第三章 寻找最大值

目录 一&#xff0c;Excel却是最基础、最高频、最有机会展示的一款数据分析工具二&#xff0c;作为数据工作者&#xff0c;实际工作中&#xff0c;不管用不用的上&#xff0c;至少到达会的水准1&#xff0c;常用函数2&#xff0c;透视表3&#xff0c;可视化4&#xff0c;数据分…
阅读更多...
【RabbitMQ笔记04】消息队列RabbitMQ七种模式之发布订阅模式（Publish/Subscribe）

【RabbitMQ笔记04】消息队列RabbitMQ七种模式之发布订阅模式（Publish/Subscribe）

这篇文章&#xff0c;主要介绍消息队列RabbitMQ七种模式之发布订阅模式&#xff08;Publish/Subscribe&#xff09;。 目录 一、发布订阅模式 1.1、Exchange交换机 &#xff08;1&#xff09;什么是Exchange交换机呢&#xff1f;&#xff1f;&#xff1f; &#xff08;2&am…
阅读更多...
数据结构与算法----问答2023

数据结构与算法----问答2023

1、什么是哈希表&#xff1f;如何解决碰撞&#xff1f; 哈希表&#xff08;Hash Table&#xff09;&#xff0c;也称为散列表&#xff0c;是一种用于实现字典&#xff08;键值对&#xff09;数据结构的数据结构。它将键映射到哈希表中的一个索引&#xff08;桶&#xff09;来保…
阅读更多...
从零开始学习iftop流量监控（找出服务器耗费流量最多的ip和端口）

从零开始学习iftop流量监控（找出服务器耗费流量最多的ip和端口）

一、iftop是什么iftop是类似于top的实时流量监控工具。作用&#xff1a;监控网卡的实时流量&#xff08;可以指定网段&#xff09;、反向解析IP、显示端口信息等官网&#xff1a;http://www.ex-parrot.com/~pdw/iftop/二、界面说明>代表发送数据&#xff0c;< 代表接收数…
阅读更多...
DHCP服务器的使用以及可能出现的问题（图文详细版）

DHCP服务器的使用以及可能出现的问题（图文详细版）

DHCP服务的使用 开始&#xff0d;管理工具&#xff0d;DHCP,打开DHCP服务器选项窗口 新建作用域 在此处输入名称和描述,单击下一步 随机确定一组IP地址的范围,并指定其子网掩码 , 单击下一步 若想要排除某一个/组特定的IP地址,我们可以在此界面输入该IP地址,若没有,则可…
阅读更多...
CTFHub | 前端验证

CTFHub | 前端验证

0x00 前言 CTFHub 专注网络安全、信息安全、白帽子技术的在线学习&#xff0c;实训平台。提供优质的赛事及学习服务&#xff0c;拥有完善的题目环境及配套 writeup &#xff0c;降低 CTF 学习入门门槛&#xff0c;快速帮助选手成长&#xff0c;跟随主流比赛潮流。 0x01 题目描述…
阅读更多...
django项目部署(腾讯云服务器centos)

django项目部署(腾讯云服务器centos)

基本步骤&#xff1a; 购买腾讯云服务器并配配置好 >> 本地项目依赖收集准备 >> 上传项目等文件到服务器 >> 服务器安装部署软件和python环境 >> 开始部署&#xff08;全局来看就这5个步骤&#xff09; 目录 目录 1. 购买腾讯云服务器并配配置好 …
阅读更多...
【算法设计技巧】分治算法

【算法设计技巧】分治算法

分治算法 用于设计算法的另一种常用技巧为分治算法(divide and conquer)。分治算法由两部分组成&#xff1a; 分(divide)&#xff1a;递归解决较小的问题(当然&#xff0c;基准情况除外)治(conquer)&#xff1a;然后&#xff0c;从子问题的解构建原问题的解。 传统上&#x…
阅读更多...
升级日记本-课后程序(JAVA基础案例教程-黑马程序员编著-第七章-课后作业)

升级日记本-课后程序(JAVA基础案例教程-黑马程序员编著-第七章-课后作业)

【实验7-4】 升级版日记本 【任务介绍】 1.任务描述 本案例要求编写一个模拟日记本的程序&#xff0c;通过在控制台输入指令&#xff0c;实现在本地新建日记本、打开日记本和修改日记本等功能。 用户输入指令1代表“新建日记本”&#xff0c;可以从控制台获取用户输入的日记…
阅读更多...
物联网MQTT协议简单介绍

物联网MQTT协议简单介绍

物联网曾被认为是继计算机、互联网之后&#xff0c;信息技术行业的第三次浪潮。随着基础通讯设施的不断完善&#xff0c;尤其是 5G 的出现&#xff0c;进一步降低了万物互联的门槛和成本。物联网本身也是 AI 和区块链应用很好的落地场景之一&#xff0c;各大云服务商也在纷纷上…
阅读更多...
mysql8.0-日志

mysql8.0-日志

目录 错误日志 错误日志主要记录如下几种日志&#xff1a; 查询日志 测试 慢查询日志 二进制日志 日志格式 日志查看 修改日志格式 二进制日志的删除 二进制日志的还原 错误日志 错误日志是MySQL中最重要的日志之一&#xff0c;它记录了当mysql启动和停止时&#xff0c;…
阅读更多...
【Python基础】类

【Python基础】类

面向对象编程 面向对象编程是最有效的软件编写方法之一。面向对象是一种对现实世界理解和抽象的方法&#xff0c;是计算机编程技术发展到一定阶段后的产物。 面向对象和面向过程的区别 比如我想吃西红柿炒蛋&#xff0c;怎么运用面向过程的方法来解决这个问题呢&#xff1f;…
阅读更多...
怕上当？来看这份网络钓鱼和诈骗技术趋势

怕上当？来看这份网络钓鱼和诈骗技术趋势

网络钓鱼和诈骗&#xff1a;当前的欺诈类型 网络钓鱼 钓鱼者可以攻击任何在线服务——银行、社交网络、政府门户网站、在线商店、邮件服务、快递公司等——中的证书。但是&#xff0c;顶级品牌的客户往往面临更大风险&#xff0c;因为相比小品牌&#xff0c;人们更喜欢使用和…
阅读更多...
12 个适合做外包项目的开源后台管理系统

12 个适合做外包项目的开源后台管理系统

1.D2admin 开源地址&#xff1a;https://github.com/d2-projects/d2-admin 文档地址&#xff1a;https://d2.pub/zh/doc/d2-admin/ 效果预览&#xff1a;https://d2.pub/d2-admin/preview/#/index 开源协议&#xff1a;MIT 2.vue-element-admin 开源地址&#xff1a;https…
阅读更多...
BACnet协议详解————MS/TP物理层，数据链路层和网络层

BACnet协议详解————MS/TP物理层，数据链路层和网络层

文章目录写在前面1 物理层2 数据链路层MSTP的流程如下noteMS/TP帧格式3 网络层写在前面 这周加更一篇&#xff0c;来弥补一下之前落下的进度。简单的说两句&#xff0c;之前讲应用层的时候&#xff0c;只是跟官方的手册来同步一下&#xff0c;但是从个人理解来说&#xff0c;自…
阅读更多...
Spring拦截器

Spring拦截器

SpringMVC提供了拦截器机制&#xff0c;允许运行目标方法之前进行一些拦截工作或者目标方法运行之后进行一下其他相关的处理。自定义的拦截器必须实现HandlerInterceptor接口。preHandle()&#xff1a;这个方法在业务处理器处理请求之前被调用&#xff0c;在该方法中对用户请求…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023