作者简介:重庆大学22级研一,研究方向:时空数据挖掘、图神经网络。目前正在学习大数据、数据挖掘等相关知识,希望毕业后能找到数据相关岗位。
前言
之前写了一个比赛复盘(【竞赛复盘】2022雪浪算力开发者大赛——阀体异常检测),发现自己存在的问题主要包括EDA做的不到位。这篇文章就以这个比赛的数据为例,简单的做一些EDA分析。没有系统学过EDA,本文内容是自己的一些拙见,还请大佬批评指正。
题目类型
首先说明一下题目类型:二分类、异常检测、时间序列。根据此,可以从以下几个方面做EDA:
- 两类样本的原始序列、衍生特征
- 能够凸显时间序列异常的特征
数据准备
(数据说明可以看复盘的文章)针对部分传感器,各取50个样本,正常样本与异常样本分开。
代码:
def get_files_list(path, station, sensor, file_num=50):
"""获取path路径下num个阀体的单个特征的list,返回一个dict"""
list_dict = {}
for sample in os.listdir(os.path.join(path,station,sensor)):
list_dict['/'.join([station, sensor, sample])] = pd.read_csv(os.path.join(path, station, sensor, sample)).iloc[:, 0]
if len(list_dict) == file_num:
return list_dict
return list_dict
# 部分传感器
sample_dict = {
'P1010': [
'MeasuredData_Pressure_Line_Input_Raw', 'MeasuredData_Temperature_Pipe_Raw',
'Report_P1010_Pressure_Clamping', 'Report_P1010_Temperature_Pipe'
],
'P1030': [
'MeasuredData_Current_Reference_Raw', 'MeasuredData_Pressure_Clamping_Raw', 'MeasuredData_Pressure_Line_Input_Raw', 'MeasuredData_Temperature_Pipe_Raw',
'Report_P1030_PI-Hysteresis-Limit_LCL_2nd_X', 'Report_P1030_Pressure-Amplitude_Rising_Y', 'Report_P1030_PI-Hysteresis-Limit_LCL_2nd_Y'
],
'P1090': [
'MeasuredData_Current_Reference_Filter', 'MeasuredData_I_Act_EVEN-PPV1_Filter', 'MeasuredData_Pressure_Line_Input_Filter',
'Report_P1090_FI-Characteristic_Falling_Y', 'Report_P1090_FI-Characteristic-Limit_UCL_X', 'Report_P1090_Force-Amplitude_Rising_LCL_X'
],
'P1130': [
'MeasuredData_Flow_Axis_LUB_Raw', 'MeasuredData_Pressure_Line_Input_Raw', 'MeasuredData_Flow_Pump_Recycle_Raw',
'Report_P1130_Flow_Clutch_LUB', 'Report_P1130_Flow_Pump_Recycle', 'Report_P1130_Flow_Axis_LUB'
]
}
# 获取异常样本
ng_valve_names = []
ng_datas = []
for station, sensors in sample_dict.items():
for sensor in sensors:
l = get_files_list(NG_PATH, station, sensor, file_num=50)
ng_valve_names.extend(list(l.keys()))
ng_datas.extend(l.values())
# 获取异常样本
ok_valve_names = []
ok_datas = []
for station, sensors in sample_dict.items():
for sensor in sensors:
l = get_files_list(OK_PATH, station, sensor, file_num=50)
ok_valve_names.extend(list(
l.keys()))
ok_datas.extend(l.values())
数据分析
统计特征分析
对样本的均值、方差、标准差、最小值、最大值可视化。
代码:
import math
def show_diff_on_line(x, ys, labels, colors, title, figsize=(20, 3), dpi=100):
"""用折线图显示不同样本的区别"""
plt.figure(figsize=figsize,dpi=dpi)
for i, y in enumerate(ys):
color = colors[i]
label = labels[i]
plt.plot(x, y, color=color, label=label)
plt.grid()
plt.title(title)
plt.legend(loc='upper right')
plt.show()
x = range(len(ng_datas))
# mean
ng_means = [data.mean() for data in ng_datas]
ok_means = [data.mean() for data in ok_datas]
show_diff_on_line(x, [ng_means, ok_means], ['ng', 'ok'], ['red', 'blue'], 'mean')
# var
ng_vars = [data.var() for data in ng_datas]
ok_vars = [data.var() for data in ok_datas]
show_diff_on_line(x, [ng_vars, ok_vars], ['ng', 'ok'], ['red', 'blue'], 'var')
# std
ng_stds = [data.std() for data in ng_datas]
ok_stds = [data.std() for data in ok_datas]
show_diff_on_line(x, [ng_stds, ok_stds], ['ng', 'ok'], ['red', 'blue'], 'std')
# min
ng_mins = [data.min() for data in ng_datas]
ok_mins = [data.min() for data in ok_datas]
show_diff_on_line(x, [ng_mins, ok_mins], ['ng', 'ok'], ['red', 'blue'], 'min')
# max
ng_mins = [data.max() for data in ng_datas]
ok_mins = [data.max() for data in ok_datas]
show_diff_on_line(x, [ng_mins, ok_mins], ['ng', 'ok'], ['red', 'blue'], 'var')
结果:
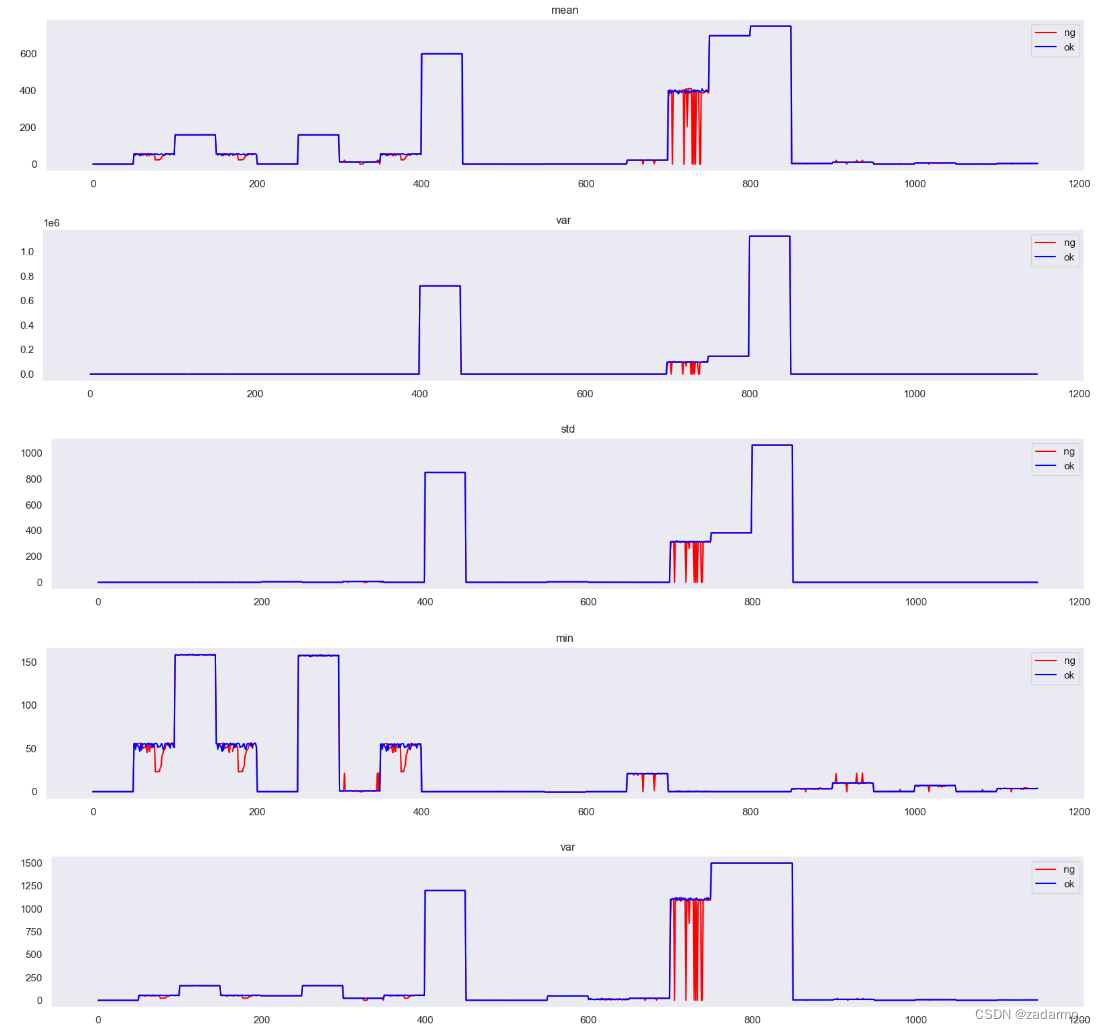
结论:
- 索引在600之前的样本在这些特征上基本没有区别,无法区分两类样本
- 索引在[700, 800]之间的样本在
mean、std、var特征上有明显区别,可以作为分类的特征
分布特征分析
对数据的四分位点、峰度、偏度分析。
代码:
# 25%
ng_25s = [data.quantile(.25) for data in ng_datas]
ok_25s = [data.quantile(.25) for data in ok_datas]
show_diff_on_line(x, [ng_25s, ok_25s], ['ng', 'ok'], ['red', 'blue'], '25%')
# 50%
ng_50s = [data.quantile(.50) for data in ng_datas]
ok_50s = [data.quantile(.50) for data in ok_datas]
show_diff_on_line(x, [ng_50s, ok_50s], ['ng', 'ok'], ['red', 'blue'], '50%')
# 75%
ng_75s = [data.quantile(.75) for data in ng_datas]
ok_75s = [data.quantile(.75) for data in ok_datas]
show_diff_on_line(x, [ng_75s, ok_75s], ['ng', 'ok'], ['red', 'blue'], '75%')
# skew
ng_skews = [data.skew() for data in ng_datas]
ok_skews = [data.skew() for data in ok_datas]
show_diff_on_line(x, [ng_skews, ok_skews], ['ng', 'ok'], ['red', 'blue'], 'skew')
# kurt
ng_kurts = [data.kurt() for data in ng_datas]
ok_kurts = [data.kurt() for data in ok_datas]
show_diff_on_line(x, [ng_kurts, ok_kurts], ['ng', 'ok'], ['red', 'blue'], 'kurt')
结果:
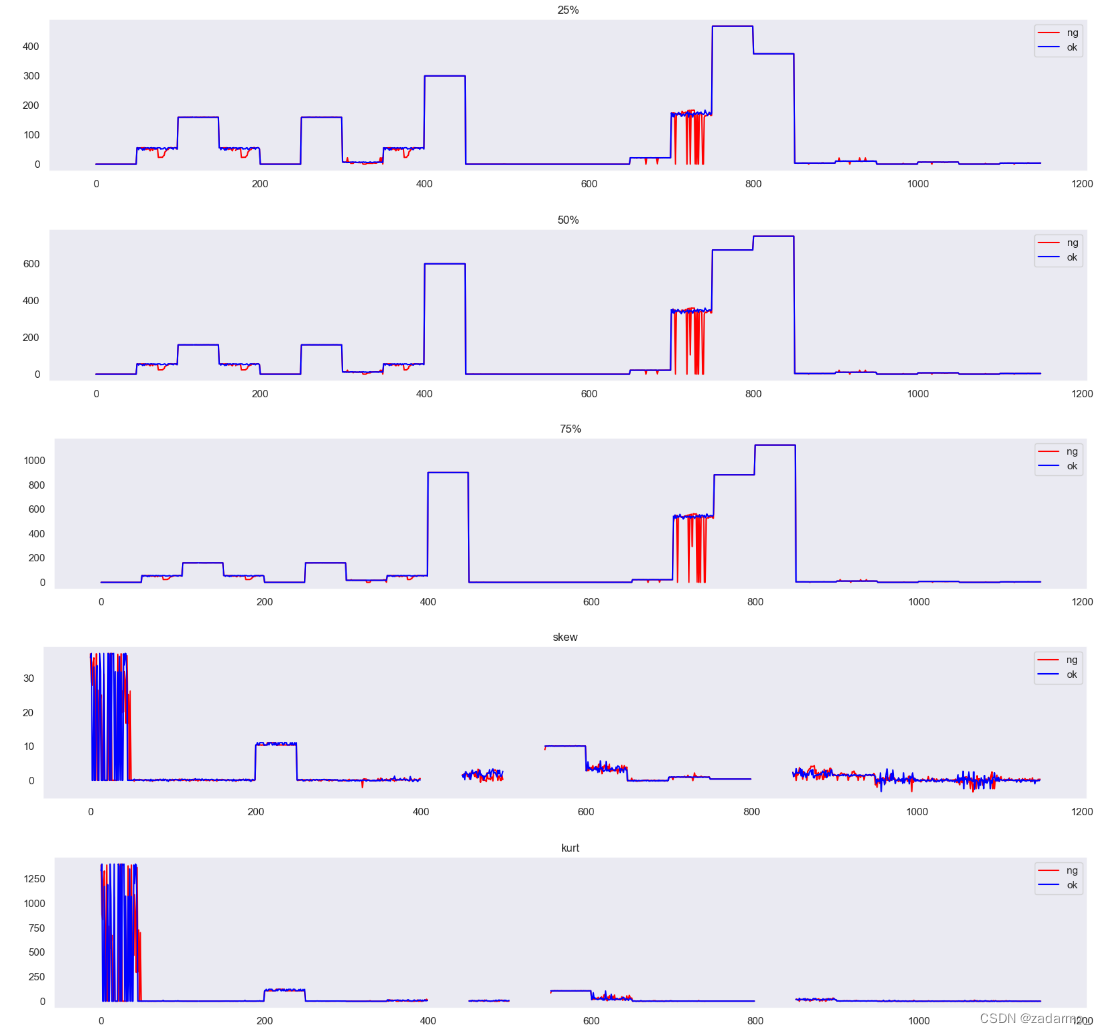
结论:
- 峰度、偏度基本没有区别
- 索引在[700, 750]的样本在四分位点上差异较大
分析到这里,可以观察到:索引在600之前的样本在这些衍生特征上都没有明显差异,所以可以假设这些传感器不利于分类。
但需要注意的是,这里分析的是单个传感器的特征。这种分析只能说明单个传感器的衍生特征不利于分类,而至于这些传感器和其他传感器是否相互影响,他们的组合衍生特征是否有利于分类,不得而知。由于组合特征比较麻烦,本文暂时就分析到这里。
异常特征差异
对箱线图异常点占比、正态分布异常点占比分析。
代码:
def get_box_outliers(s: pd.Series):
"""返回箱线图异常点"""
q1, q3 = s.quantile(.25), s.quantile(.75)
iqr = q3 - q1
low, up = q1 - 1.5*iqr, q3 + 1.5*iqr
outliers = s[(s > up) | (s < low)]
return outliers
def get_normal_outliers(s: pd.Series):
"""返回正态分布异常点"""
low = s.mean() - 3 * s.std()
up = s.mean() + 3 * s.std()
outliers = s[(s > up) | (s < low)]
return outliers
x = range(len(ng_datas))
ng_outliers = [len(get_box_outliers(data)) / len(data) if len(data) != 0 else 0 for data in ng_datas ]
ok_outliers = [len(get_box_outliers(data)) / len(data) if len(data) != 0 else 0 for data in ok_datas]
show_diff_on_line(x, [ng_outliers, ok_outliers], ['ng', 'ok'], ['red', 'blue'], 'box-line outliers')
ng_outliers = [len(get_normal_outliers(data)) / len(data) if len(data) != 0 else 0 for data in ng_datas ]
ok_outliers = [len(get_normal_outliers(data)) / len(data) if len(data) != 0 else 0 for data in ok_datas]
show_diff_on_line(x, [ng_outliers, ok_outliers], ['ng', 'ok'], ['red', 'blue'], '3σ outliers')
结果:
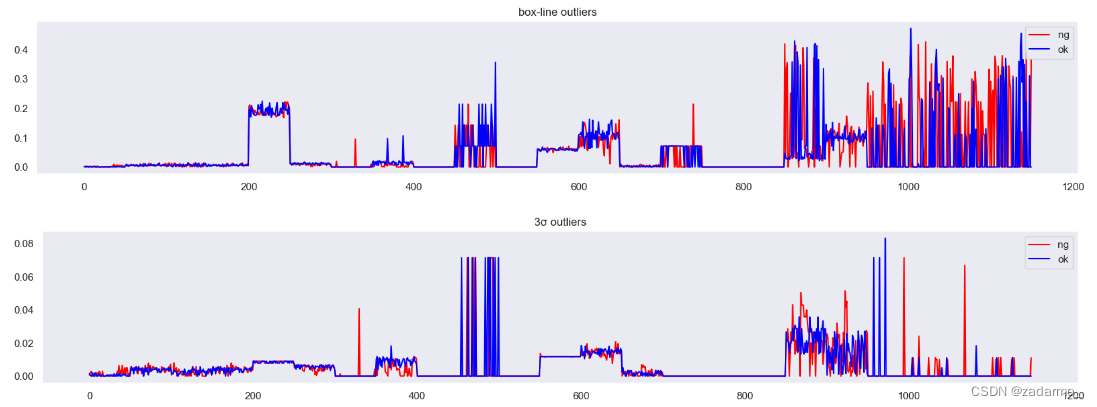
结论:
- 索引在800之后的样本的这两个特征差异较大,有利于分类
- 箱线图异常点比例 比 正态分布异常点比例 更容易区分两类样本
总结
- 由于通常数据量较大,不可能对所有样本的所有特征进行EDA。本文中采取的是抽样的方式进行分析,分析结论有一定的局限性,但结论也对于建模有一定的帮助,可以通过建模的结果来对EDA进行改进、完善
- 本文采用的都是折线图,所得结论有限。后续进一步学习数据分析,了解有哪些常用于时间序列分析的特征以及图表