0.前言

本篇博客已经把两个关于栈的OJ题分块，可以根据目录跳转，并且代码已经上传至gitee可自取。

1.最小栈

155. 最小栈 - 力扣（LeetCode）

1.1 原题展示

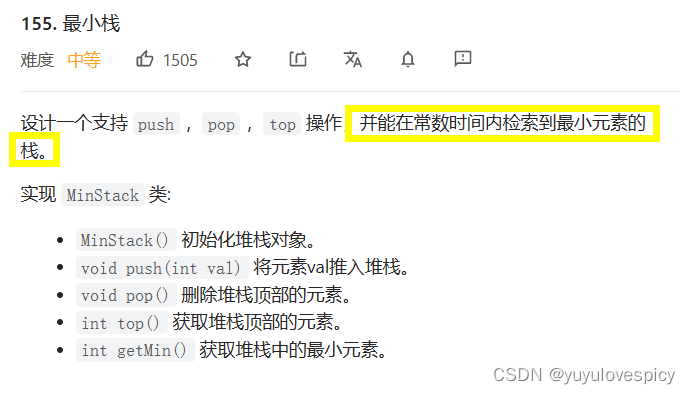
本题需要我们设计一个栈，这个栈相对于普通的栈，有一个特异功能，可以在常数O（1）的时间复杂度下直接找到并返回，现在栈内所有元素的最小值是多少。

这个要设计的有特异功能的栈，我们称之为最小栈，本题就是要实现一个MinStack类。多了一个特异接口getMin。

1.2 思路分析

1.2.1 场景引入

我们如何实时记录当前栈的最小值呢？有人说，我们可以在MinStack类当中记录一个int _min成员，每次插入之后，我们对比一下这个_min，如果插入的数据比当前的_min更小的话，那就更新_min，这样不就可以实时记录当前最小值吗？

class MinStack {
private:
    stack<int> _st;
    int _min;
};

但是这样并不能的哦，如果你删除数据呢？如果你删除一个当前的_min值元素，那你能知道，现在删除完_min元素之后，栈的新最小值_min是什么，需要更新什么值呢？这就不知道了吧！！！

所以我们的思路是再存一个存放最小值的容器，这个容器负责存储如果每次删除完_min最小值之后，可以从这个容器当中再找到次小的_min的值。

从时序角度上来说，一个栈的最小值，肯定是一浪更比一浪强，前浪被拍在沙滩上。在插入数据的过程中，一个栈内数据的最小值是不断的被更新成越来越小的。相反，在删除数据的过程中，如果我们删除了现在的最小值（后浪），我们应该把曾经作为最小值的值（被拍死的前浪），作为新的最小值。

栈这个容器，是后进先出，先进后出，我们的记录的最小值：先被作为最小值（被拍死的前浪们）的元素是后出的；最新一次作为最小值的元素，肯定是优先被删除的，后成为最小值的值要先出。所以我们选取栈作为记录每次最小值的容器。

class MinStack {
private:
    stack<int> _st;
    stack<int> _min_st;

1.2.2 思路

所以我们除了定义一个主栈_st，存储所有插入的数据，还要定义一个最小栈_min_st，用来存储每次当前栈的最小值，始终维持这个最小栈的栈顶元素始终代表当前的最小值。

如果我们在主栈当中插入一个比当前栈最小值_min，还要更小的一个数据more min，那么我们就在最小栈当中插入以记录这个更小的一个数据。而如果是一个插入更大的数据，那就没有必要动最小栈_min_st，此时最小值不变。

如果我们在主栈当中删除了当前栈的最小值，那么我们也要在最小栈进行出栈操作，去除更新当前的最小值，出栈之后，那接下来最小栈的栈顶，就变成了次小的最小值，此时最小栈的栈顶仍然代表着当前栈的最小值！

1.3 代码实现

1.3.1 最小栈的删除

最小栈的栈顶数据代表当前栈内所有数据的最小值，如果删除的是当前最小值，那要顺便再对最小栈出栈，更新为次小值为最小值！

void pop() {
        //我们删除还要看删除的是否在现在的最小栈中
        int val = _st.top();
        if(val == _min_st.top()) //是最小栈的该元素，要删除
        {
            _st.pop();
            _min_st.pop();
        }
        else //不是最小栈中的元素，就可以直接出栈,然后现在min_st中的顶还是最小值
        {
            _st.pop();
        }
    }

1.3.2 最小栈的插入

插入比当前最小值更小的数据，更新入栈_min_st，或者还有一种特殊情况，如果是一个空栈，我们也要更新入栈_min_st！

如果插入比当前最小值还大的数据，那么我们就没有必要动最小栈_min_st。

而如果插入的是和当前最小值相等的数据，那么我们入不入最小栈呢？不管入不入栈，都不会影响当前栈的最小值的记录，这样看入不入的确没有太大关系。可是你想一想，如果你遇到相等最小值的时候，不入最小栈的话，在删除逻辑中，如果你删除了这个最小值，那么我们如果出栈_min_st，那此时最小栈的栈顶元素就不能代表当前栈内元素的最小值了。

例如，你依次插入了 2 3 4 1 1，那最小栈从栈底到栈顶就依次是2 1，如果我要删除1，那主栈内就变为2 3 4 1，那我最小栈就会变成2，此时最小栈栈顶就不是当前栈的最小值。

所以如果插入的是和当前最小值相等的数据，也要入最小栈。

void push(int val) {
        _st.push(val);
        if(_min_st.empty())
        {
            _min_st.push(val);
        }
        else //不是空
        {
            //如果出现了更小的val，那就入栈
            if(val<=_min_st.top()) //相等的情况也必须入栈，不然我们删除的时候就不知道最小值在栈底还有多个的情况
            {
                _min_st.push(val);
            }
            //否则更大的val就不用入栈了
        }
    }

1.3.3 获取栈顶元素

返回主栈的栈顶。

int top() {
        return _st.top();
    }

1.3.4 获取当前栈的最小值

返回最小栈的栈顶。

int getMin() {
        return _min_st.top();
    }

2. 有效的括号

20. 有效的括号 - 力扣（LeetCode）

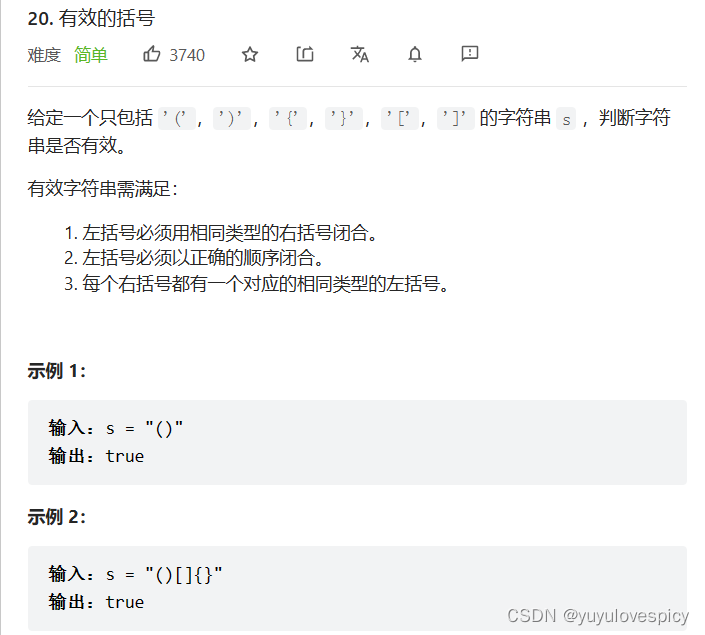
就是给你一个括号序列，看看这个是否是一个有效的括号序列。那么什么是有效的括号呢？其实就是最近的一个左括号和离得它最近的右括号能够相互匹配，也可以说是一个右括号和离得它最近的左括号能够相互匹配（匹配的意思是 "(" 只能去匹配 ")" ，"{" 只能去匹配 "}" ，"[" 只能去匹配 "]" ）

这里用栈结构即可很好的解决，如果遇到了左括号，那么就入栈，等待最近一个右括号的匹配（先进后出，后进先出，一定是后面的左括号先被匹配，前面的括号后被匹配，这完美的符合栈的性质），如果遇到了右括号，那么我们就出栈顶数据，即找到最近的一个左括号，进行匹配检查，如果不匹配，那就return false，如果匹配就继续检查。

转换成代码就是这样的：

bool isValid(char * s){
    此时就可以利用栈先进后出的特性进行判断*/
    //遍历遇到左括号，则入栈
    //遍历遇到右括号，则出栈数据对右括号进行匹配
    //到最后遍历匹配完毕，栈为空即可【这是针对左括号多出来的情况】
    //【而右括号多出来的情况，则是栈中没有数据与之匹配了，此时也不是有效的括号false】

    //定义一个栈
    Stack st;
    StackInit(&st);
    //遍历字符串括号集
    while(*s!='\0')
    {
        //遇到左括号
        if(*s == '{' || *s == '[' || *s=='(')
        {
            StackPush(&st,*s);
        }
        else{//遇到右括号
            //判断非法情况,右括号多余左括号
            if(StackEmpty(&st))
            {
                return false;
            }
            //出栈和右括号进行匹配
            int left_brace = StackTop(&st);
            StackPop(&st);
            //不匹配则false，匹配则继续遍历比较
            if(left_brace=='{'&&*s != '}'
            || left_brace=='['&&*s != ']'
            || left_brace=='('&&*s != ')'
            ){
                return false;
            }
        }
        ++s;
    }
    //判断非法情况,左括号多余右括号
    return StackEmpty(&st);
}