神经网络

知识点

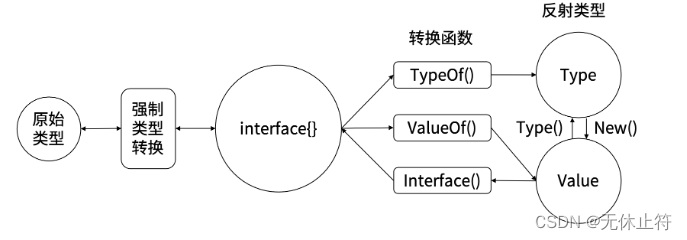
M-P神经元

模型如图所示：

 神经元的工作机理：神经元接收来到n个其他神经元传递过来的输入信号，这些输入信号通过带权重的连接进行传递，神经元接收到的总输入值将与神经元的阈值进行比较，然后通过"激活函数"处理以产生神经元的输出。
单个M-P神经元：感知机（sgn作激活函数）、对数几率回归（sigmoid作激活函数）

多个M-P神经元：神经网络

感知机模型

 激活函数为sgn（阶跃函数）的神经元：

 若两类模式是线性可分的，即存在一个线性超平面将它们分开，如图5.4（a）-（c）所示，则感知机的学习过程一定会收敛而求得适当的权向量W，否则感知机学习过程将会发生振荡，W难以稳定下来，不能求得合适解，例如感知机不能解决（d）所示的异或这样简单的非线性可分问题。

 要解决非线性可分问题，需考虑使用多层功能神经元，如下图，简单的两层感知机就能解决异或问题。

权重调整：

神经网络

 通用近似定理：只需一个包含足够多神经元的隐层，多层前馈网络就能以任意精度逼近任意复杂度的连续函数，因此，神经网络既能做回归，也能做分类，而且不需要复杂的特征工程。
 多层前馈神经网络：每层神经元与下一层神经元全互连，神经元之间不存在同层连接，也不存在跨层连接。

 误差逆传播（BP）算法：

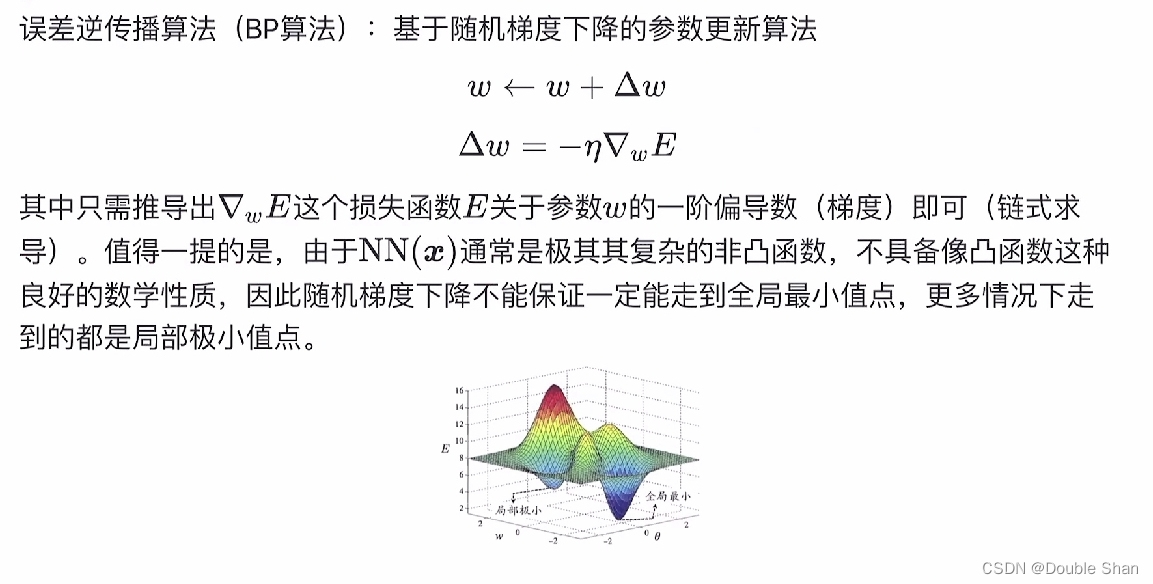
通常说“BP网络”时，一般是指用BP算法训练的多层前馈神经网络。
 BP算法的工作流程：先将输入示例提供给输入层神经元，然后逐层将信号前传，直到产生输出层的结果；然后计算输出层的误差，再将误差逆向传播至隐层神经元，最后根据隐层神经元的误差来对阈值和连接权进行调整，该迭代过程循环进行，直到达到某些停止条件为止，例如：训练误差已达到一个很小的值。
 目标：要最小化训练集上的累积误差，一般来说，标准BP算法每次只针对单个样例，参数更新得非常频繁，而且对不同的样例进行更新的效果可能出现“抵消”现象。