leetcode 31~40 学习经历
- 31. 下一个排列
- 32. 最长有效括号
- 33. 搜索旋转排序数组
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 35. 搜索插入位置
- 36. 有效的数独
- 37. 解数独
- 38. 外观数列
- 39. 组合总和
- 40. 组合总和 II
- 小结
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 100
通过次数402,089提交次数1,052,132
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/next-permutation
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
猛的一看,题目很简单,直接写了一个后数比前数大就交换的小代码,类似冒泡一样,一提交。。。。结果错误了
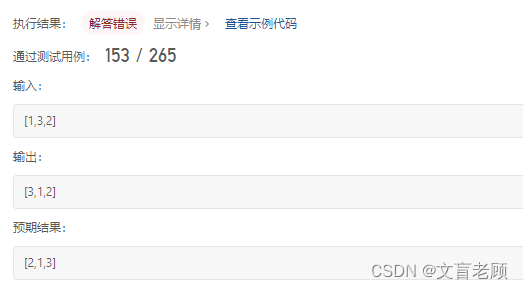
[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] ,这是题意说明里举例的原内容啊。。。结果你告诉我你的预期结果是另一个?那我就得从新思考一下流程了啊
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
应该是这么排列了吧?那么也就是说,隐藏了一个条件,当数字需要前移时,如果后边有小于前边数字的,优先移动小数字啊,否则简单判断后数比前数小,那么2 1 3和2 3 1就不会出现了,嗯,思路的问题,之前的没有考虑到这个问题,从新写
比预计的时间长了点才写出来,还是错了一大堆用例才弄明白移动方式
class Solution:
def move(self,arr):
f1 = arr[1]
up = [n for n in arr[2:] if n > arr[0]]
if len(up) == 0:
arr.pop(1)
else:
f1 = min(up)
arr.pop(arr.index(f1))
arr.sort()
return [f1] + arr
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
#nums = [3,2,1]
do = False
n = len(nums)
for i in range(n,1,-1):
if nums[i - 1] > nums[i - 2]:
do = True
reverse = self.move(nums[i - 2:])
for j in range(len(reverse)):
nums[n - len(reverse) + j] = reverse[j]
break
if not do:
reverse = nums[::-1]
for i in range(n):
nums[i] = reverse[i]
关键就是移动后,后边的部分要排序,如果后边部分有比前移位置大的数字,让最小的比前移数字大的数字放前边,思路问题。。。。脑袋秀逗的厉害,自己坑了自己一把。
啊。。。看了大佬的答案之后,原来 nums[:] = … 不影响引用,学到了学废了,更精巧的算法,大佬有提供了,还真是学废了
32. 最长有效括号
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = “(()”
输出:2
解释:最长有效括号子串是 “()”
示例 2:
输入:s = “)()())”
输出:4
解释:最长有效括号子串是 “()()”
示例 3:
输入:s = “”
输出:0
提示:
0 <= s.length <= 3 * 10^4
s[i] 为 ‘(’ 或 ‘)’
通过次数348,000提交次数937,871
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-valid-parentheses
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
又是猛一看很简单,一提交解答错误。。。好吧,真是意想不到,先弄个勉强能用的版本出来
class Solution:
def longestValidParentheses(self, s: str) -> int:
#s = ')()())'
n = []
t = list(s)
for i in range(len(s)):
if s[i] == '(':
n.append(s[i])
elif s[i] == ')' and (len(n) == 0 or n[-1] != '('):
n = []
else:
n.pop(-1)
t[i] = '.'
t[i - t[:i][::-1].index('(') - 1] = '.'
return max([len(n) for n in ''.join(t).replace('(',')').split(')')])
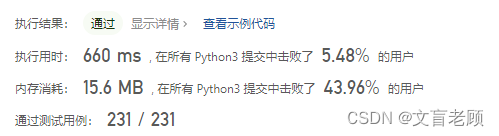
由于会出现很长的字符串,所以优化一下字符串截取部分
class Solution:
def longestValidParentheses(self, s: str) -> int:
#s = ')()())'
n = []
t = []
mx = 0
for i in range(len(s)):
if s[i] == '(':
n.append('(')
t.append('(')
elif s[i] == ')' and (len(n) == 0 or n[-1] != '('):
mx = max(mx,max([len(n) for n in ''.join(t).replace('(',')').split(')')]))
n = []
t = []
else:
n.pop(-1)
t.append('.')
t[len(t) - t[::-1].index('(') - 1] = '.'
mx = max(mx,max([len(n) for n in ''.join(t).replace('(',')').split(')')]))
return mx
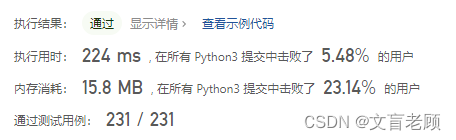
成绩还是很差啊,一会再弄个看看,先不找大佬们的答案
class Solution:
def longestValidParentheses(self, s: str) -> int:
n = len(s)
t = list(s)
mx = 0
for i in range(n):
if t[i] == ')' and i > 0:
j = 1
while i - j >= 0 and t[i - j] in '(.':
if t[i - j] == '(':
t[i] = '.'
t[i - j] = '.'
while i - j >= 0 and t[i - j] == '.':
j += 1
mx = max(mx,j)
break
j += 1
return mx

因为是循环向前找合法的,所以我在这里用点来代替合法的位置,效率还是不太好,那么再弄一版看看
class Solution:
def longestValidParentheses(self, s: str) -> int:
d = {}
mx = 0
for i in range(len(s)):
if s[i] == ')' and i > 0: # 如果是右括号才进行验证
if s[i - 1] == '(': # 如果上一个字符是左括号,则当前位置合法
d[i] = i - 1 # 将当前位置和上一个字符位置记录到字典
elif i - 1 in d and d[i - 1] - 1 >= 0 and s[d[i - 1] - 1] == '(':
# 如果上一个字符不是左括号,但是,上一个位置已经合法
# 且上一个合法位置之前也是左括号,则是括号嵌套,当前位置合法
d[i] = d[i - 1] - 1 # 记录当前位置及上一个合法前的位置
del d[i - 1] # 删除上一个位置合法的字典信息
if i in d: # 如果当前位置合法,检测合法位置之前的一个位置是否合法
if d[i] > 0 and d[i] - 1 in d: # 如果也合法则合并
t = d[i] - 1
d[i] = d[d[i] - 1]
del d[t]
mx = max(mx,i - d[i] + 1) # 计算长度
return mx
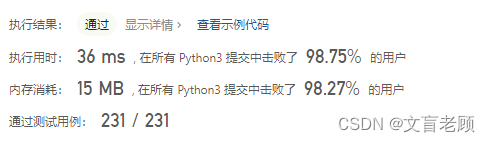
呦,成绩不错,现在可以去看大佬们的答案了
28ms dp 解题。。。32ms 栈解题(问题是我没看明白逻辑)

黑人问号脸。。。。。。回头再琢磨这个
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
示例 3:
输入:nums = [1], target = 0
输出:-1
提示:
1 <= nums.length <= 5000
-10^4 <= nums[i] <= 10^4
nums 中的每个值都 独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-10^4 <= target <= 10^4
通过次数688,143提交次数1,569,131
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/search-in-rotated-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
O(log n) 是个啥级别?比 O(n) 还要小的么?算了,一会搞,先上个搞笑的
class Solution:
def search(self, nums: List[int], target: int) -> int:
return nums.index(target) if nums.count(target) > 0 else -1
再来个暴力 O(n) 的
class Solution:
def search(self, nums: List[int], target: int) -> int:
for i in range(len(nums)):
if nums[i] == target:
return i
return - 1
最后,来个一个上了两次二分查找的,代码就不上了,有点累赘
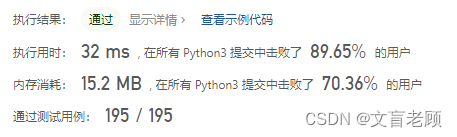
然后。。。20ms大佬只用了一次二分查找就可以了。。。。嗯,又学废了一次,老顾这思路僵化的厉害
34. 在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9
nums 是一个非递减数组
-10^9 <= target <= 10^9
通过次数728,738提交次数1,717,709
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
又是一个二分查找的题,但令人疑惑的是,什么叫非递减数组?有过排序的吗?[0,1,2,-1,-2] 这个算非递减数组吗?无序数组算非递减数组吗?如果是无序数组的话,应该不能用二分查找吧?
算了,直接暴力O(n)来一次
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
r = [-1,-1]
for i in range(len(nums)):
if nums[i] == target:
r[0] = i if r[0] == -1 else r[0]
r[1] = i
return r
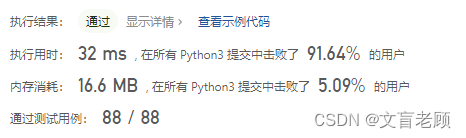
额。。。这个成绩有点意外了,如果是这样的效率,执行二分查找还有意义吗?试着来一次看看
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
al,ar = -1,-1
l,r = 0,len(nums) - 1
while l <= r:
m = (l + r) // 2
if nums[m] < target:
l = m + 1
elif nums[m] > target:
r = m - 1
else:
al,ar = m,m
while al > 0 and nums[al - 1] == target:
al -= 1
while ar< len(nums) - 1 and nums[ar + 1] == target:
ar += 1
break
if l == r and nums[l] != target:
break
return [al,ar]
不知道这个题目考核目的是什么,难道是命中 target 之后,继续二分查找第一个target和最后一个target?二分查找做成函数,递归调用?
总之很疑惑,20ms的用了两次二分查找,怎么保证第一次命中,正好是target左边界?
继续疑惑,24ms用迭代,这和循环不差不多嘛?
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
1 <= nums.length <= 10^4
-10^4 <= nums[i] <= 10^4
nums 为 无重复元素 的 升序 排列数组
-10^4 <= target <= 10^4
通过次数1,064,915提交次数2,361,450
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/search-insert-position
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
哦吼,排序数组,嗯,降序的也算,嘿嘿,这连续二分查找,是题海强化战术吗?
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
#target,nums = 0,[1,3]
if len(nums) == 1:
if nums[0] == target:
return 0
if nums[0] < target:
return 1
else:
return 0
l,r = 0,len(nums) - 1
t = nums[0] < nums[-1]
while l < r:
m = (l + r) // 2
if nums[m] == target:
return m
if nums[m] < target:
if t:
l = m + 1
else:
r = m - 1
else:
if t:
r = m - 1
else:
l = m + 1
if l >= r:
l = max(l,r)
if t:
if nums[l] < target:
return l + 1
else:
return l
else:
if nums[l] < target:
return l
else:
return l - 1
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
if len(nums) == 1:
if nums[0] == target:
return 0
if nums[0] < target:
return 1
else:
return 0
l,r = 0,len(nums) - 1
while l < r:
m = (l + r) // 2
if nums[m] == target:
return m
if nums[m] < target:
l = m + 1
else:
r = m - 1
if l >= r:
l = max(l,r)
if nums[l] < target:
return l + 1
else:
return l
果然是我想多了,他就是升序的数组
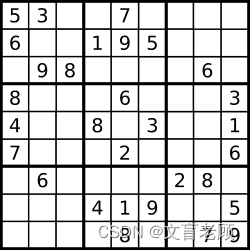
36. 有效的数独
请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
空白格用 ‘.’ 表示。
示例 1:
输入:board =
[[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:true
示例 2:
输入:board =
[[“8”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”]
,[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”]
,[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”]
,[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”]
,[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”]
,[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”]
,[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”]
,[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”]
,[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:false
解释:除了第一行的第一个数字从 5 改为 8 以外,空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字(1-9)或者 ‘.’
通过次数352,119提交次数556,389
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/valid-sudoku
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
想起来很久很久以前,报纸上有解数独有奖活动,我还写了个js版的解,嗯,发现下一题就是解数独了。
行吧,先完成这个,在进行怀旧
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
for i in range(9):
row = board[i]
if len([n for n in row if row.count(n) > 1 and n != '.']) > 0:
return False
col = [row[i] for row in board]
if len([n for n in col if col.count(n) > 1 and n != '.']) > 0:
return False
cel = [[row[i % 3 * 3 + 0],row[i % 3 * 3 + 1],row[i % 3 * 3 + 2]] for row in [board[i // 3 * 3],board[i // 3 * 3 + 1],board[i // 3 * 3 + 2]]]
block = cel[0] + cel[1] + cel[2]
if len([n for n in block if block.count(n) > 1 and n != '.']) > 0:
return False
return True
没啥好说的,行列块分别验证没有重复数字即可,然后看了看大佬们的回答,不用统计,自行建立数组,然后将指定位置的数插入到数组里,有重复就跳出,20ms真大佬,这真学不了,变量定义位置,定义类型,这是有自己的书写习惯,真没法改了
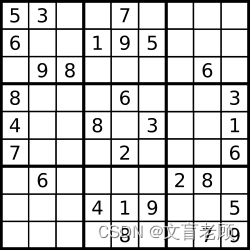
37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例 1:
输入:board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解
通过次数189,597提交次数280,420
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/sudoku-solver
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
嗯嗯,解数独,05年那会比较熟,印象就只有一个了,就是解的时候,有4种可能,结果现在写了一段代码后,发现自己只会两种了。。。。哭。。。这和编程没关系了啊!
经历了一天,没解出第二个用例。。。我是指我自己人工解,毕竟自己没思路就没法解了
先放出暂时的代码,之后再补有算法的,我这个就是硬抗的。。。。
# 这个用例,我人工没解出来
board = [[".",".","9","7","4","8",".",".","."],["7",".",".",".",".",".",".",".","."],[".","2",".","1",".","9",".",".","."],[".",".","7",".",".",".","2","4","."],[".","6","4",".","1",".","5","9","."],[".","9","8",".",".",".","3",".","."],[".",".",".","8",".","3",".","2","."],[".",".",".",".",".",".",".",".","6"],[".",".",".","2","7","5","9",".","."]]
# 这个用例测试通过
#board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
class Solution:
def getPoint(self,i,j):
blk = [i // 3,j // 3]
rows = [self.dp[n + blk[0] * 3] for n in range(3)]
cols = [[row[n + blk[1] * 3] for row in self.dp] for n in range(3)]
cell = [[self.dp[n + blk[0] * 3][s + blk[1] * 3] for s in range(3)] for n in range(3)]
cur_row = rows[i % 3]
rows.pop(i % 3)
cur_col = cols[j % 3]
cols.pop(j % 3)
block = cell[0] + cell[1] + cell[2]
single_row = 3 - len([n for n in cell[i % 3] if n.isnumeric()]) == 1
single_cel = 3 - len([n[j % 3] for n in cell if n[j % 3].isnumeric()]) == 1
useable = list(self.dic - set(cur_row + cur_col + block))
for n in useable:
if n in rows[0] and n in rows[1] and n in cols[0] and n in cols[1]:
#print(i,j,useable,n,'other rows and cols used')
useable = [n]
break
if single_row and n in rows[0] and n in rows[1]:
#print(i,j,useable,n,'only one row in block,and other rows used')
useable = [n]
break
if single_cel and n in cols[0] and n in cols[1]:
#print(i,j,useable,n,'only one col in block,and other cols used')
useable = [n]
break
return useable
def do(self):
result = False
for i in range(9):
for j in range(9):
if i * 10 + j in self.over:
continue
if self.dp[i][j].isnumeric():
self.over.add(i * 10 + j)
continue
n = self.getPoint(i, j)
if len(n) == 1:
self.dp[i][j] = n[0]
#print('position:{},{} ==> {}'.format(i,j,n[0]))
self.over.add(i * 10 + j)
result = True
return result
def useableNumer(self):
result = {}
for i in range(9):
for j in range(9):
if i * 10 + j in self.over:
continue
if self.dp[i][j].isnumeric():
continue
result[i * 10 + j] = self.getPoint(i, j)
return result
def solveSudoku(self, board: list[list[str]]) -> None:
self.dp = board
self.over = set()
self.dic = set(list('123456789'))
deep = 0
while self.do():
deep += 1
#print(self.useableNumer())
#for row in self.dp:
# print(' '.join(row))
return
s = Solution()
s.solveSudoku(board)
for row in s.dp:
print(' '.join(row))
然后是一个噩梦般的晚上,睡梦里全是这个没解开的数独。。。。。辗转反侧啊。。。。
一早起来,赶紧把题做完。。。加了一个穷举试数的过程,结果就。。。完成了
class Solution:
def getPoint(self,i,j):
blk = [i // 3,j // 3]
rows = [self.dp[n + blk[0] * 3] for n in range(3)]
cols = [[row[n + blk[1] * 3] for row in self.dp] for n in range(3)]
cell = [[self.dp[n + blk[0] * 3][s + blk[1] * 3] for s in range(3)] for n in range(3)]
cur_row = rows[i % 3]
rows.pop(i % 3)
cur_col = cols[j % 3]
cols.pop(j % 3)
block = cell[0] + cell[1] + cell[2]
single_row = 3 - len([n for n in cell[i % 3] if n.isnumeric()]) == 1
single_cel = 3 - len([n[j % 3] for n in cell if n[j % 3].isnumeric()]) == 1
useable = list(self.dic - set(cur_row + cur_col + block))
for n in useable:
if n in rows[0] and n in rows[1] and n in cols[0] and n in cols[1]:
#print(i,j,useable,n,'other rows and cols used')
useable = [n]
break
if single_row and n in rows[0] and n in rows[1]:
#print(i,j,useable,n,'only one row in block,and other rows used')
useable = [n]
break
if single_cel and n in cols[0] and n in cols[1]:
#print(i,j,useable,n,'only one col in block,and other cols used')
useable = [n]
break
return useable
def do(self):
result = False
pos = 0
while pos < len(self.blank):
i = self.blank[pos] // 10
j = self.blank[pos] % 10
n = self.getPoint(i, j)
if len(n) == 1:
self.dp[i][j] = n[0]
self.blank.pop(pos)
result = True
else:
pos += 1
return result
def guess(self,arr):
if len(arr) == 0:
return True
i = arr[0] // 10
j = arr[0] % 10
n = self.getPoint(i, j)
if len(n) == 0:
return False
for l in range(len(n)):
self.dp[i][j] = n[l]
F = self.guess(arr[1:])
if F:
return F
self.dp[i][j] = '.'
return False
def solveSudoku(self, board: list[list[str]]) -> None:
self.dp = board
self.dic = set(list('123456789'))
self.blank = []
deep = 0
for i in range(9):
for j in range(9):
if self.dp[i][j].isnumeric():
continue
self.blank.append(i * 10 + j)
while self.do():
deep += 1
self.guess(self.blank)
return
。。。。。这才6个用例啊。。。白瞎我写了这么长代码,结合36题,我都可以做数独游戏了。嗯。。。。力扣37题评论区还真有人这么说了
38. 外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
111211211111221第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 “11”
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 “21”
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 “1211”
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 “111221”
要 描述 一个数字字符串,首先要将字符串分割为 最小 数量的组,每个组都由连续的最多 相同字符 组成。然后对于每个组,先描述字符的数量,然后描述字符,形成一个描述组。要将描述转换为数字字符串,先将每组中的字符数量用数字替换,再将所有描述组连接起来。
例如,数字字符串 “3322251” 的描述如下图:
示例 1:
输入:n = 1
输出:“1”
解释:这是一个基本样例。
示例 2:
输入:n = 4
输出:“1211”
解释:
countAndSay(1) = “1”
countAndSay(2) = 读 “1” = 一 个 1 = “11”
countAndSay(3) = 读 “11” = 二 个 1 = “21”
countAndSay(4) = 读 “21” = 一 个 2 + 一 个 1 = “12” + “11” = “1211”
提示:
1 <= n <= 30
通过次数327,264提交次数542,498
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/count-and-say
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
额。。。。这个题目凭什么是中等难度?难道除了初学者,还有谁不会写递归的吗?更不要说在这里刷题的,各位大佬哪个不是针针计较的优化效率,递归也算考点?
class Solution:
def countAndSay(self, n: int) -> str:
if n == 1:
return '1'
s = self.countAndSay(n - 1)
r = ''
c = s[0]
l = 1
for i in range(1,len(s)):
if s[i] != c:
r += str(l) + c
c = s[i]
l = 1
else:
l += 1
r += str(l) + c
return r
随便谢谢,然后看看大佬们的答案,这题就过了
然后,我天真了。。。。。20ms和24ms的大佬这是欺负这个用例少,范围才30。。。然后,自己把30个值都计算出来了(只一遍调用30,每次递归输出即可),然后扔到数组、词典里,直接根据输入的数返回,连计算都没了。。。。。真@作弊
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
示例 2:
输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]
示例 3:
输入: candidates = [2], target = 1
输出: []
提示:
1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40
通过次数677,503提交次数933,089
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这题也是中等,明显比上一题难不少啊,老顾最怕的就是这种组合题,前边2数,3数,4数就已经很怕了,这个不定的更怕,只会无穷递归。。。
class Solution:
def combinationSum(self, candidates: list[int], target: int) -> list[list[int]]:
arr = [n for n in candidates if n <= target]
arr.sort(reverse = True)
z = []
for i in range(len(arr)):
z += self.makeGroup(arr[i:],target,[])
r = []
for i in z:
i.sort()
if i not in r:
r.append(i)
r.sort()
return r
def makeGroup(self,arr,target,nums):
#print(nums,target)
if len(nums) > 0 and nums[0] == 8:
print(nums,arr)
if target == 0:
return [nums]
if len(arr) == 0:
return []
if target - arr[-1] < 0:
return []
r = []
for i in range(target // arr[0] + 1):
r += self.makeGroup(arr[1:],target - arr[0] * i,nums + [arr[0] for _ in range(i)])
return r
明显需要优化的地方太多了
class Solution:
def combinationSum(self, candidates: list[int], target: int) -> list[list[int]]:
arr = [n for n in candidates if n <= target]
arr.sort(reverse = True)
return self.makeGroup(arr,target,[])
def makeGroup(self,arr,target,nums):
if target == 0:
return [nums]
if len(arr) == 0:
return []
if target - arr[-1] < 0:
return []
r = []
for i in range(target // arr[0] + 1):
g = nums + [arr[0] for _ in range(i)]
n = self.makeGroup(arr[1:],target - arr[0] * i,g)
for z in n:
if z not in r:
r.append(z)
return r
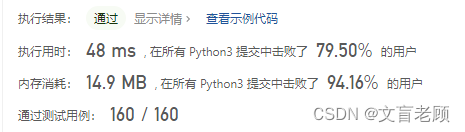
整体还是无穷递归,感觉还在吃灰的路上啊
class Solution:
def combinationSum(self, candidates: list[int], target: int) -> list[list[int]]:
def makeGroup(arr,target,nums):
if target == 0:
z.append(nums)
return
if len(arr) == 0:
return
if target - arr[-1] < 0:
return
for i in range(target // arr[0] + 1):
makeGroup(arr[1:],target - arr[0] * i,nums + [arr[0] for _ in range(i)])
arr = [n for n in candidates if n <= target]
arr.sort(reverse = True)
z = []
makeGroup(arr,target,[])
return z

原来,不用return值,直接修改局部变量,效率会提高一点点啊。。。
40. 组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[[1,1,6],[1,2,5],[1,7],[2,6]]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
输出:
[[1,2,2],[5]]
提示:
1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30
通过次数394,476提交次数655,590
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/combination-sum-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
和上一题一样的路子?不过每个数用一次?应该没啥区别吧?
class Solution:
def combinationSum2(self, candidates: list[int], target: int) -> list[list[int]]:
arr = [n for n in candidates if n <= target]
arr.sort(reverse=True)
z = []
def makeGroup(arr,target,nums):
if target == 0 and nums not in z:
z.append(nums)
if len(arr) == 0:
return
if target < arr[-1]:
return
if target == arr[0]:
z.append(nums + [target])
pos = 0
while pos < len(arr):
while pos < len(arr) and pos > 0 and arr[pos] == arr[pos - 1]:
pos += 1
continue
if pos == len(arr):
break
makeGroup(arr[pos + 1:],target - arr[pos],nums + [arr[pos]])
pos += 1
makeGroup(arr, target, [])
return z
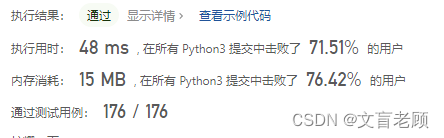
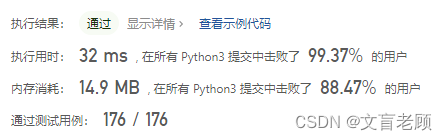
嗯,和上一题还是差不多,不过一个循环加自己,一个循环加下一个
小结
这10题除了解数独,其他真心不好说有多少难度,31题32题也就卡了一下下,转过思路其实也还算友好。
数独这个是真不会了,以前的解法看来还有些缺陷,用例第二个就不去了,我先发文,后边再补数独这个