Tensor 介绍

一、Tensor 的概念介绍

飞桨使用张量（Tensor）来表示神经网络中传递的数据，Tensor 可以理解为多维数组，类似于 Numpy 数组（ndarray）的概念。与 Numpy 数组相比，Tensor 除了支持运行在 CPU 上，还支持运行在 GPU 及各种 AI 芯片上，以实现计算加速；此外，飞桨基于 Tensor，实现了深度学习所必须的反向传播功能和多种多样的组网算子，从而可更快捷地实现深度学习组网与训练等功能。两者具体异同点可参见下文 Tensor 与 Numpy 数组相互转换。

在飞桨框架中，神经网络的输入、输出数据，以及网络中的参数均采用 Tensor 数据结构，示例如下：

def train(model):
    model.train()
    epochs = 2
    optim = paddle.optimizer.Adam(learning_rate=0.001, parameters=model.parameters())
    # 模型训练的两层循环
    for epoch in range(epochs):
        for batch_id, data in enumerate(train_loader()):
            x_data = data[0]
            y_data = data[1]
            print("x_data: ", x_data[0][0][0][0]) # 打印神经网络的输入：批数据中的第一个数据的第一个元素
            predicts = model(x_data)
            print("predicts: ", predicts[0]) # 打印神经网络的输出：批数据中的第一个数据的第一个元素
            print("weight: ", model.linear1.weight[0][0]) # 打印神经网络的权重：linear1 层的 weight 中的第一个元素
            loss = F.cross_entropy(predicts, y_data)
            acc = paddle.metric.accuracy(predicts, y_data)
            loss.backward()
            optim.step()
            optim.clear_grad()
            break
        break
model = LeNet()
train(model)

x_data:  Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [-1.])
predicts:  Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [-0.72636688])
weight:  Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=False,
       [0.02227839])

以上示例代码来源使用 LeNet 在 MNIST 数据集实现图像分类（篇幅原因仅截取部分），分别打印了神经网络的输入、输出数据和网络中的参数，可以看到均采用了 Tensor 数据结构。

二、Tensor 的创建

飞桨可基于给定数据手动创建 Tensor，并提供了多种方式，如：

2.1 指定数据创建

2.2 指定形状创建

2.3 指定区间创建

另外在常见深度学习任务中，数据样本可能是图片（image）、文本（text）、语音（audio）等多种类型，在送入神经网络训练或推理前均需要创建为 Tensor。飞桨提供了将这类数据手动创建为 Tensor 的方法，如：

2.4 指定图像、文本数据创建

由于这些操作在整个深度学习任务流程中比较常见且固定，飞桨在一些 API 中封装了 Tensor 自动创建的操作，从而无须手动转 Tensor。

2.5 自动创建 Tensor 的功能介绍

如果你熟悉 Numpy，已经使用 Numpy 数组创建好数据，飞桨可以很方便地将 Numpy 数组转为 Tensor，具体介绍如：

六、Tensor 与 Numpy 数组相互转换

2.1 指定数据创建

与 Numpy 创建数组方式类似，通过给定 Python 序列（如列表 list、元组 tuple），可使用 paddle.to_tensor 创建任意维度的 Tensor。示例如下：

2.1.1 创建类似向量（vector）的 1 维 Tensor：

import paddle # 后面的示例代码默认已导入 paddle 模块
ndim_1_Tensor = paddle.to_tensor([2.0, 3.0, 4.0])
print(ndim_1_Tensor)

Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [2., 3., 4.])

特殊地，如果仅输入单个标量（scalar）数据（例如 float/int/bool 类型的单个元素），则会创建形状为 [1] 的 Tensor，即 0 维 Tensor：

paddle.to_tensor(2)
paddle.to_tensor([2])

# 上述两种创建方式完全一致，形状均为 [1]，输出如下：
Tensor(shape=[1], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [2])

2.1.2 创建类似矩阵（matrix）的 2 维 Tensor：

ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0, 3.0],
                                  [4.0, 5.0, 6.0]])
print(ndim_2_Tensor)

Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[1., 2., 3.],
        [4., 5., 6.]])

2.1.3 创建 3 维 Tensor：

ndim_3_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
print(ndim_3_Tensor)

Tensor(shape=[2, 2, 5], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [[[1 , 2 , 3 , 4 , 5 ],
         [6 , 7 , 8 , 9 , 10]],
        [[11, 12, 13, 14, 15],
         [16, 17, 18, 19, 20]]])

上述不同维度的 Tensor 可视化的表示如下图所示：

图 1 不同维度的 Tensor 可视化表示

需要注意的是，Tensor 必须形如矩形，即在任何一个维度上，元素的数量必须相等，否则会抛出异常，示例如下：

ndim_2_Tensor = paddle.to_tensor([[1.0, 2.0],
                                  [4.0, 5.0, 6.0]])

ValueError:
        Failed to convert input data to a regular ndarray :
         - Usually this means the input data contains nested lists with different lengths.

说明：

飞桨也支持将 Tensor 转换为 Python 序列数据，可通过 paddle.tolist 实现，飞桨实际的转换处理过程是 Python 序列 <-> Numpy 数组 <-> Tensor。
基于给定数据创建 Tensor 时，飞桨是通过拷贝方式创建，与原始数据不共享内存。

2.2 指定形状创建

如果要创建一个指定形状的 Tensor，可以使用 paddle.zeros、paddle.ones、paddle.full 实现。

paddle.zeros([m, n])             # 创建数据全为 0，形状为 [m, n] 的 Tensor
paddle.ones([m, n])              # 创建数据全为 1，形状为 [m, n] 的 Tensor
paddle.full([m, n], 10)          # 创建数据全为 10，形状为 [m, n] 的 Tensor

例如，paddle.ones([2,3])输出如下：

Tensor(shape=[2, 3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[1., 1., 1.],
        [1., 1., 1.]])

2.3 指定区间创建

如果要在指定区间内创建 Tensor，可以使用paddle.arange、 paddle.linspace 实现。

paddle.arange(start, end, step)  # 创建以步长 step 均匀分隔区间[start, end)的 Tensor
paddle.linspace(start, stop, num) # 创建以元素个数 num 均匀分隔区间[start, stop)的 Tensor

示例如下：

paddle.arange(start=1, end=5, step=1)

Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [1, 2, 3, 4])

说明：

除了以上指定数据、形状、区间创建 Tensor 的方法，飞桨还支持如下类似的创建方式，如：

创建一个空 Tensor，即根据 shape 和 dtype 创建尚未初始化元素值的 Tensor，可通过 paddle.empty 实现。
创建一个与其他 Tensor 具有相同 shape 与 dtype 的 Tensor，可通过 paddle.ones_like 、 paddle.zeros_like 、 paddle.full_like 、paddle.empty_like 实现。
拷贝并创建一个与其他 Tensor 完全相同的 Tensor，可通过 paddle.clone 实现。
创建一个满足特定分布的 Tensor，如 paddle.rand, paddle.randn , paddle.randint 等。
通过设置随机种子创建 Tensor，可每次生成相同元素值的随机数 Tensor，可通过 paddle.seed 和 paddle.rand 组合实现。

2.4 指定图像、文本数据创建

在常见深度学习任务中，数据样本可能是图片（image）、文本（text）、语音（audio）等多种类型，在送入神经网络训练或推理前，这些数据和对应的标签均需要创建为 Tensor。以下是图像场景和 NLP 场景中手动转换 Tensor 方法的介绍。

对于图像场景，可使用 paddle.vision.transforms.ToTensor 直接将 PIL.Image 格式的数据转为 Tensor，使用 paddle.to_tensor 将图像的标签（Label，通常是 Python 或 Numpy 格式的数据）转为 Tensor。
对于文本场景，需将文本数据解码为数字后，再通过 paddle.to_tensor 转为 Tensor。不同文本任务标签形式不一样，有的任务标签也是文本，有的则是数字，均需最终通过 paddle.to_tensor 转为 Tensor。

下面以图像场景为例介绍，以下示例代码中将随机生成的图片转换为 Tensor。

import numpy as np
from PIL import Image
import paddle.vision.transforms as T
import paddle.vision.transforms.functional as F
fake_img = Image.fromarray((np.random.rand(224, 224, 3) * 255.).astype(np.uint8)) # 创建随机图片
transform = T.ToTensor()
tensor = transform(fake_img) # 使用 ToTensor()将图片转换为 Tensor
print(tensor)

Tensor(shape=[3, 224, 224], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [[[0.78039223, 0.72941178, 0.34117648, ..., 0.76470596, 0.57647061, 0.94901967],
         ...,
         [0.49803925, 0.72941178, 0.80392164, ..., 0.08627451, 0.97647065, 0.43137258]]])

说明：

实际编码时，由于飞桨数据加载的 paddle.io.DataLoader API 能够将原始 paddle.io.Dataset 定义的数据自动转换为 Tensor，所以可以不做手动转换。具体如下节介绍。

2.5 自动创建 Tensor 的功能介绍

除了手动创建 Tensor 外，实际在飞桨框架中有一些 API 封装了 Tensor 创建的操作，从而无需用户手动创建 Tensor。例如 paddle.io.DataLoader 能够基于原始 Dataset，返回读取 Dataset 数据的迭代器，迭代器返回的数据中的每个元素都是一个 Tensor。另外在一些高层 API，如 paddle.Model.fit 、paddle.Model.predict ，如果传入的数据不是 Tensor，会自动转为 Tensor 再进行模型训练或推理。

说明：

paddle.Model.fit、paddle.Model.predict 等高层 API 支持传入 Dataset 或 DataLoader，如果传入的是 Dataset，那么会用 DataLoader 封装转为 Tensor 数据；如果传入的是 DataLoader，则直接从 DataLoader 迭代读取 Tensor 数据送入模型训练或推理。因此即使没有写将数据转为 Tensor 的代码，也能正常执行，提升了编程效率和容错性。
以下示例代码中，分别打印了原始数据集的数据，和送入 DataLoader 后返回的数据，可以看到数据结构由 Python list 转为了 Tensor。

import paddle
from paddle.vision.transforms import Compose, Normalize
transform = Compose([Normalize(mean=[127.5],
                               std=[127.5],
                               data_format='CHW')])
test_dataset = paddle.vision.datasets.MNIST(mode='test', transform=transform)
print(test_dataset[0][1]) # 打印原始数据集的第一个数据的 label
loader = paddle.io.DataLoader(test_dataset)
for data in enumerate(loader):
    x, label = data[1]
    print(label) # 打印由 DataLoader 返回的迭代器中的第一个数据的 label
    break

[7] # 原始数据中 label 为 Python list
Tensor(shape=[1, 1], dtype=int64, place=Place(gpu_pinned), stop_gradient=True,
       [[7]]) # 由 DataLoader 转换后，label 为 Tensor

三、Tensor 的属性

在前文中，可以看到打印 Tensor 时有 shape、dtype、place 等信息，这些都是 Tensor 的重要属性，想要了解如何操作 Tensor 需要对其属性有一定了解，接下来分别展开介绍 Tensor 的属性相关概念。

Tensor(shape=[3], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [2., 3., 4.])

3.1 Tensor 的形状（shape）

3.1.1 形状的介绍

形状是 Tensor 的一个重要的基础属性，可以通过 Tensor.shape 查看一个 Tensor 的形状，以下为相关概念：

shape：描述了 Tensor 每个维度上元素的数量。
ndim： Tensor 的维度数量，例如向量的维度为 1，矩阵的维度为 2，Tensor 可以有任意数量的维度。
axis 或者 dimension：Tensor 的轴，即某个特定的维度。
size：Tensor 中全部元素的个数。

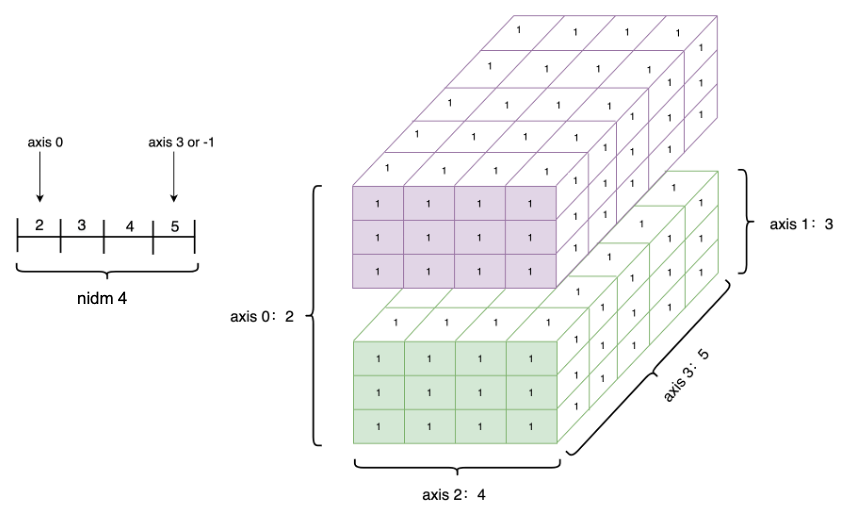
创建 1 个四维 Tensor ，并通过图形来直观表达以上几个概念之间的关系：

ndim_4_Tensor = paddle.ones([2, 3, 4, 5])

图 2 Tensor 的 shape、axis、dimension、ndim 之间的关系

print("Data Type of every element:", ndim_4_Tensor.dtype)
print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])

Data Type of every element: paddle.float32
Number of dimensions: 4
Shape of Tensor: [2, 3, 4, 5]
Elements number along axis 0 of Tensor: 2
Elements number along the last axis of Tensor: 5

3.1.2 重置 Tensor 形状（Reshape）的方法

重新设置 Tensor 的 shape 在深度学习任务中比较常见，如一些计算类 API 会对输入数据有特定的形状要求，这时可通过 paddle.reshape 接口来改变 Tensor 的 shape，但并不改变 Tensor 的 size 和其中的元素数据。

以下示例代码中，创建 1 个 shape=[3] 的一维 Tensor，使用 reshape 功能将该 Tensor 重置为 shape=[1, 3] 的二维 Tensor。这种做法经常用在把一维的标签（label）数据扩展为二维，由于飞桨框架中神经网络通常需要传入一个 batch 的数据进行计算，因此可将数据增加一个 batch 维，方便后面的数据计算。

ndim_1_Tensor = paddle.to_tensor([1, 2, 3])
print("the shape of ndim_1_Tensor:", ndim_1_Tensor.shape)
reshape_Tensor = paddle.reshape(ndim_1_Tensor, [1, 3])
print("After reshape:", reshape_Tensor.shape)

the shape of ndim_1_Tensor: [3]
After reshape: [1, 3]

在指定新的 shape 时存在一些技巧：

-1 表示这个维度的值是从 Tensor 的元素总数和剩余维度自动推断出来的。因此，有且只有一个维度可以被设置为 -1。
0 表示该维度的元素数量与原值相同，因此 shape 中 0 的索引值必须小于 Tensor 的维度（索引值从 0 开始计，如第 1 维的索引值是 0，第二维的索引值是 1）。

通过几个例子来详细了解：

origin:[3, 2, 5] reshape:[3, 10]      actual: [3, 10] # 直接指定目标 shape
origin:[3, 2, 5] reshape:[-1]         actual: [30] # 转换为 1 维，维度根据元素总数推断出来是 3*2*5=30
origin:[3, 2, 5] reshape:[-1, 5]      actual: [6, 5] # 转换为 2 维，固定一个维度 5，另一个维度根据元素总数推断出来是 30÷5=6
origin:[3, 2, 5] reshape:[0, -1]      actual: [3, 10] # reshape:[0, -1]中 0 的索引值为 0，按照规则，转换后第 0 维的元素数量与原始 Tensor 第 0 维的元素数量相同，为 3；第 1 维的元素数量根据元素总值计算得出为 30÷3=10。
origin:[3, 2]    reshape:[3, 1, 0]    error： # reshape:[3, 1, 0]中 0 的索引值为 2，但原 Tensor 只有 2 维，无法找到与第 3 维对应的元素数量，因此出错。

从上面的例子可以看到，通过 reshape:[-1] ，可以很方便地将 Tensor 按其在计算机上的内存分布展平为一维。

print("Tensor flattened to Vector:", paddle.reshape(ndim_3_Tensor, [-1]).numpy())

Tensor flattened to Vector: [1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]

说明：

除了 paddle.reshape 可重置 Tensor 的形状，还可通过如下方法改变 shape：

paddle.squeeze，可实现 Tensor 的降维操作，即把 Tensor 中尺寸为 1 的维度删除。
paddle.unsqueeze，可实现 Tensor 的升维操作，即向 Tensor 中某个位置插入尺寸为 1 的维度。
paddle.flatten，将 Tensor 的数据在指定的连续维度上展平。
paddle.transpose，对 Tensor 的数据进行重排。
3.1.3 原位（Inplace）操作和非原位操作的区别

飞桨框架的 API 有原位（Inplace）操作和非原位操作之分，原位操作即在原 Tensor 上保存操作结果，输出 Tensor 将与输入 Tensor 共享数据，并且没有 Tensor 数据拷贝的过程。非原位操作则不会修改原 Tensor，而是返回一个新的 Tensor。通过 API 名称区分两者，如 paddle.reshape 是非原位操作，paddle.reshape_ 是原位操作。

下面以 reshape 为例说明，通过对比 Tensor 的 name （每个 Tensor 创建时都会有一个独一无二的 name），判断是否为同一个 Tensor。

origin_tensor = paddle.to_tensor([1, 2, 3])
new_tensor = paddle.reshape(origin_tensor, [1, 3]) # 非原位操作
same_tensor = paddle.reshape_(origin_tensor, [1, 3]) # 原位操作
print("origin_tensor name: ", origin_tensor.name)
print("new_tensor name: ", new_tensor.name)
print("same_tensor name: ", same_tensor.name)

origin_tensor name:  generated_tensor_0
new_tensor name:  auto_0_ # 非原位操作后产生的 Tensor 与原始 Tensor 的名称不同
same_tensor name:  generated_tensor_0 # 原位操作后产生的 Tensor 与原始 Tensor 的名称相同

3.2 Tensor 的数据类型（dtype）

3.2.1 指定数据类型的介绍

Tensor 的数据类型 dtype 可以通过 Tensor.dtype 查看，支持类型包括：bool、float16、float32、float64、uint8、int8、int16、int32、int64、complex64、complex128。

同一 Tensor 中所有元素的数据类型均相同，通常通过如下方式指定：

通过给定 Python 序列创建的 Tensor，可直接使用 dtype 参数指定。如果未指定：
- 对于 Python 整型数据，默认会创建 int64 型 Tensor；
- 对于 Python 浮点型数据，默认会创建 float32 型 Tensor，并且可以通过 paddle.set_default_dtype 来调整浮点型数据的默认类型。

# 创建 Tensor 时指定 dtype
ndim_1_tensor = paddle.to_tensor([2.0, 3.0, 4.0], dtype='float64')
print("Tensor dtype of ndim_1_tensor:", ndim_1_tensor.dtype)
# 创建 Tensor 时不指定 dtype，自动选择对应的默认类型
print("Tensor dtype from Python integers:", paddle.to_tensor(1).dtype)
print("Tensor dtype from Python floating point:", paddle.to_tensor(1.0).dtype)

Tensor dtype of ndim_1_tensor: paddle.float64
Tensor dtype from Python integers: paddle.int64
Tensor dtype from Python floating point: paddle.float32

通过 Numpy 数组或其他 Tensor 创建的 Tensor，则与其原来的数据类型保持相同。
Tensor 不仅支持 float、int 类型数据，也支持 complex 复数类型数据。如果输入为复数，则 Tensor 的 dtype 为 complex64 或 complex128 ，其每个元素均为 1 个复数。如果未指定，默认数据类型是complex64：

ndim_2_Tensor = paddle.to_tensor([[(1+1j), (2+2j)],
                                  [(3+3j), (4+4j)]])
print(ndim_2_Tensor)

Tensor(shape=[2, 2], dtype=complex64, place=Place(gpu:0), stop_gradient=True,
       [[(1+1j), (2+2j)],
        [(3+3j), (4+4j)]])

3.2.2 修改数据类型的方法

飞桨框架提供了paddle.cast 接口来改变 Tensor 的 dtype：

float32_Tensor = paddle.to_tensor(1.0)
float64_Tensor = paddle.cast(float32_Tensor, dtype='float64')
print("Tensor after cast to float64:", float64_Tensor.dtype)
int64_Tensor = paddle.cast(float32_Tensor, dtype='int64')
print("Tensor after cast to int64:", int64_Tensor.dtype)

Tensor after cast to float64: paddle.float64
Tensor after cast to int64: paddle.int64

3.3 Tensor 的设备位置（place）

初始化 Tensor 时可以通过 Tensor.place 来指定其分配的设备位置，可支持的设备位置有：CPU、GPU、固定内存、XPU（Baidu Kunlun）、NPU（Huawei）、MLU（寒武纪）、IPU（Graphcore）等。其中固定内存也称为不可分页内存或锁页内存，其与 GPU 之间具有更高的读写效率，并且支持异步传输，这对网络整体性能会有进一步提升，但其缺点是分配空间过多时可能会降低主机系统的性能，因为其减少了用于存储虚拟内存数据的可分页内存。

说明：

当未指定 place 时，Tensor 默认设备位置和安装的飞桨框架版本一致。如安装了 GPU 版本的飞桨，则设备位置默认为 GPU，即 Tensor 的place 默认为 paddle.CUDAPlace。
使用 paddle.device.set_device 可设置全局默认的设备位置。Tensor.place 的指定值优先级高于全局默认值。
以下示例分别创建了 CPU、GPU 和固定内存上的 Tensor，并通过 Tensor.place 查看 Tensor 所在的设备位置：

创建 CPU 上的 Tensor

cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
print(cpu_Tensor.place)

Place(cpu)

创建 GPU 上的 Tensor

gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print(gpu_Tensor.place) # 显示 Tensor 位于 GPU 设备的第 0 张显卡上

Place(gpu:0)

创建固定内存上的 Tensor

pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print(pin_memory_Tensor.place)

Place(gpu_pinned)

3.4 Tensor 的名称（name）

Tensor 的名称是其唯一的标识符，为 Python 字符串类型，查看一个 Tensor 的名称可以通过 Tensor.name 属性。默认地，在每个 Tensor 创建时，会自定义一个独一无二的名称。

print("Tensor name:", paddle.to_tensor(1).name)

Tensor name: generated_tensor_0

3.5 Tensor 的 stop_gradient 属性

stop_gradient 表示是否停止计算梯度，默认值为 True，表示停止计算梯度，梯度不再回传。在设计网络时，如不需要对某些参数进行训练更新，可以将参数的 stop_gradient 设置为 True。可参考以下代码直接设置 stop_gradient 的值。

eg = paddle.to_tensor(1)
print("Tensor stop_gradient:", eg.stop_gradient)
eg.stop_gradient = False
print("Tensor stop_gradient:", eg.stop_gradient)

Tensor stop_gradient: True
Tensor stop_gradient: False

四、Tensor 的操作

4.1 索引和切片

通过索引或切片方式可访问或修改 Tensor。飞桨框架使用标准的 Python 索引规则与 Numpy 索引规则，与 Indexing a list or a string in Python 类似。具有以下特点：

基于 0-n 的下标进行索引，如果下标为负数，则从尾部开始计算。
通过冒号 : 分隔切片参数，start:stop:step 来进行切片操作，其中 start、stop、step 均可缺省。

4.1.1 访问 Tensor

针对一维 Tensor，仅有单个维度上的索引或切片：

ndim_1_Tensor = paddle.to_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
print("Origin Tensor:", ndim_1_Tensor.numpy())          # 原始 1 维 Tensor
print("First element:", ndim_1_Tensor[0].numpy())       # 取 Tensor 第一个元素的值
print("Last element:", ndim_1_Tensor[-1].numpy())       # 取 Tensor 最后一个元素的值
print("All element:", ndim_1_Tensor[:].numpy())         # 取 Tensor 所有元素的值
print("Before 3:", ndim_1_Tensor[:3].numpy())           # 取 Tensor 前三个元素的值
print("From 6 to the end:", ndim_1_Tensor[6:].numpy())  # 取 Tensor 第六个以后的值
print("From 3 to 6:", ndim_1_Tensor[3:6].numpy())       # 取 Tensor 第三个至第六个之间的值
print("Interval of 3:", ndim_1_Tensor[::3].numpy())     # 取 Tensor 从第一个开始，间距为 3 的下标的值
print("Reverse:", ndim_1_Tensor[::-1].numpy())          # 取 Tensor 翻转后的值

Origin Tensor: [0 1 2 3 4 5 6 7 8])
First element: [0]
Last element: [8]
All element: [0 1 2 3 4 5 6 7 8]
Before 3: [0 1 2]
From 6 to the end: [6 7 8]
From 3 to 6: [3 4 5]
Interval of 3: [0 3 6]
Reverse: [8 7 6 5 4 3 2 1 0]

针对二维及以上的 Tensor，则会有多个维度上的索引或切片：

ndim_2_Tensor = paddle.to_tensor([[0, 1, 2, 3],
                                  [4, 5, 6, 7],
                                  [8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor.numpy())
print("First row:", ndim_2_Tensor[0].numpy())
print("First row:", ndim_2_Tensor[0, :].numpy())
print("First column:", ndim_2_Tensor[:, 0].numpy())
print("Last column:", ndim_2_Tensor[:, -1].numpy())
print("All element:", ndim_2_Tensor[:].numpy())
print("First row and second column:", ndim_2_Tensor[0, 1].numpy())

Origin Tensor: [[ 0  1  2  3]
                [ 4  5  6  7]
                [ 8  9 10 11]]
First row: [0 1 2 3]
First row: [0 1 2 3]
First column: [0 4 8]
Last column: [ 3  7 11]
All element: [[ 0  1  2  3]
              [ 4  5  6  7]
              [ 8  9 10 11]]
First row and second column: [1]

索引或切片的第一个值对应第 0 维，第二个值对应第 1 维，依次类推，如果某个维度上未指定索引，则默认为 : 。例如：

ndim_2_Tensor[1]
ndim_2_Tensor[1, :]

这两种操作的结果是完全相同的。

Tensor(shape=[4], dtype=int64, place=Place(gpu:0), stop_gradient=True,
       [4, 5, 6, 7])

4.1.2 修改 Tensor

与访问 Tensor 类似，修改 Tensor 可以在单个或多个维度上通过索引或切片操作。同时，支持将多种类型的数据赋值给该 Tensor，当前支持的数据类型有：int，float，numpy.ndarray，complex，Tensor。

注意：

请慎重通过索引或切片修改 Tensor，该操作会原地修改该 Tensor 的数值，且原值不会被保存。如果被修改的 Tensor 参与梯度计算，仅会使用修改后的数值，这可能会给梯度计算引入风险。飞桨框架会自动检测不当的原位（inplace）使用并报错。

import numpy as np
x = paddle.to_tensor(np.ones((2, 3)).astype(np.float32)) # [[1., 1., 1.], [1., 1., 1.]]
x[0] = 0                      # x : [[0., 0., 0.], [1., 1., 1.]]
x[0:1] = 2.1                  # x : [[2.09999990, 2.09999990, 2.09999990], [1., 1., 1.]]
x[...] = 3                    # x : [[3., 3., 3.], [3., 3., 3.]]
x[0:1] = np.array([1,2,3])    # x : [[1., 2., 3.], [3., 3., 3.]]
x[1] = paddle.ones([3])       # x : [[1., 2., 3.], [1., 1., 1.]]

同时，飞桨还提供了丰富的 Tensor 操作的 API，包括数学运算、逻辑运算、线性代数等 100 余种 API，这些 API 调用有两种方法：

x = paddle.to_tensor([[1.1, 2.2], [3.3, 4.4]], dtype="float64")
y = paddle.to_tensor([[5.5, 6.6], [7.7, 8.8]], dtype="float64")
print(paddle.add(x, y), "\n") # 方法一：使用 Paddle 的 API
print(x.add(y), "\n") # 方法二：使用 tensor 类成员函数

Tensor(shape=[2, 2], dtype=float64, place=Place(gpu:0), stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])
Tensor(shape=[2, 2], dtype=float64, place=Place(gpu:0), stop_gradient=True,
       [[6.60000000 , 8.80000000 ],
        [11.        , 13.20000000]])

可以看出，使用 Tensor 类成员函数 和 Paddle API 具有相同的效果，由于 类成员函数 操作更为方便，以下均从 Tensor 类成员函数 的角度，对常用 Tensor 操作进行介绍。

4.2 数学运算

x.abs()                       #逐元素取绝对值
x.ceil()                      #逐元素向上取整
x.floor()                     #逐元素向下取整
x.round()                     #逐元素四舍五入
x.exp()                       #逐元素计算自然常数为底的指数
x.log()                       #逐元素计算 x 的自然对数
x.reciprocal()                #逐元素求倒数
x.square()                    #逐元素计算平方
x.sqrt()                      #逐元素计算平方根
x.sin()                       #逐元素计算正弦
x.cos()                       #逐元素计算余弦
x.add(y)                      #逐元素相加
x.subtract(y)                 #逐元素相减
x.multiply(y)                 #逐元素相乘
x.divide(y)                   #逐元素相除
x.mod(y)                      #逐元素相除并取余
x.pow(y)                      #逐元素幂运算
x.max()                       #指定维度上元素最大值，默认为全部维度
x.min()                       #指定维度上元素最小值，默认为全部维度
x.prod()                      #指定维度上元素累乘，默认为全部维度
x.sum()                       #指定维度上元素的和，默认为全部维度

飞桨框架对 Python 数学运算相关的魔法函数进行了重写，例如：

x + y  -> x.add(y)            #逐元素相加
x - y  -> x.subtract(y)       #逐元素相减
x * y  -> x.multiply(y)       #逐元素相乘
x / y  -> x.divide(y)         #逐元素相除
x % y  -> x.mod(y)            #逐元素相除并取余
x ** y -> x.pow(y)            #逐元素幂运算

4.3 逻辑运算

x.isfinite()                  #判断 Tensor 中元素是否是有限的数字，即不包括 inf 与 nan
x.equal_all(y)                #判断两个 Tensor 的全部元素是否相等，并返回形状为[1]的布尔类 Tensor
x.equal(y)                    #判断两个 Tensor 的每个元素是否相等，并返回形状相同的布尔类 Tensor
x.not_equal(y)                #判断两个 Tensor 的每个元素是否不相等
x.less_than(y)                #判断 Tensor x 的元素是否小于 Tensor y 的对应元素
x.less_equal(y)               #判断 Tensor x 的元素是否小于或等于 Tensor y 的对应元素
x.greater_than(y)             #判断 Tensor x 的元素是否大于 Tensor y 的对应元素
x.greater_equal(y)            #判断 Tensor x 的元素是否大于或等于 Tensor y 的对应元素
x.allclose(y)                 #判断 Tensor x 的全部元素是否与 Tensor y 的全部元素接近，并返回形状为[1]的布尔类 Tensor

同样地，飞桨框架对 Python 逻辑比较相关的魔法函数进行了重写，以下操作与上述结果相同。

x == y  -> x.equal(y)         #判断两个 Tensor 的每个元素是否相等
x != y  -> x.not_equal(y)     #判断两个 Tensor 的每个元素是否不相等
x < y   -> x.less_than(y)     #判断 Tensor x 的元素是否小于 Tensor y 的对应元素
x <= y  -> x.less_equal(y)    #判断 Tensor x 的元素是否小于或等于 Tensor y 的对应元素
x > y   -> x.greater_than(y)  #判断 Tensor x 的元素是否大于 Tensor y 的对应元素
x >= y  -> x.greater_equal(y) #判断 Tensor x 的元素是否大于或等于 Tensor y 的对应元素

以下操作仅针对 bool 型 Tensor：

x.logical_and(y)              #对两个布尔类型 Tensor 逐元素进行逻辑与操作
x.logical_or(y)               #对两个布尔类型 Tensor 逐元素进行逻辑或操作
x.logical_xor(y)              #对两个布尔类型 Tensor 逐元素进行逻辑亦或操作
x.logical_not(y)              #对两个布尔类型 Tensor 逐元素进行逻辑非操作

4.4 线性代数

x.t()                         #矩阵转置
x.transpose([1, 0])           #交换第 0 维与第 1 维的顺序
x.norm('fro')                 #矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                #矩阵（x-y）的 2 范数
x.matmul(y)                   #矩阵乘法

注意

以上计算 API 也有原位（inplace）操作和非原位操作之分，如x.add(y)是非原位操作，x.add_(y)为原位操作。

五、Tensor 的广播机制

在深度学习任务中，有时需要使用较小形状的 Tensor 与较大形状的 Tensor 执行计算，广播机制就是将较小形状的 Tensor 扩展到与较大形状的 Tensor 一样的形状，便于匹配计算，同时又没有对较小形状 Tensor 进行数据拷贝操作，从而提升算法实现的运算效率。
飞桨框架提供的一些 API 支持广播（broadcasting）机制，允许在一些运算时使用不同形状的 Tensor。
飞桨 Tensor 的广播机制主要遵循如下规则（参考 Numpy 广播机制）：

每个 Tensor 至少为一维 Tensor。
从最后一个维度向前开始比较两个 Tensor 的形状，需要满足如下条件才能进行广播：两个 Tensor 的维度大小相等；或者其中一个 Tensor 的维度等于 1；或者其中一个 Tensor 的维度不存在。

举例如下：

# 可以广播的例子 1
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 4))
# 两个 Tensor 形状一致，可以广播
z = x + y
print(z.shape)
# [2, 3, 4]

# 可以广播的例子 2
x = paddle.ones((2, 3, 1, 5))
y = paddle.ones((3, 4, 1))
# 从最后一个维度向前依次比较：
# 第一次：y 的维度大小是 1
# 第二次：x 的维度大小是 1
# 第三次：x 和 y 的维度大小相等
# 第四次：y 的维度不存在
# 所以 x 和 y 是可以广播的
z = x + y
print(z.shape)
# [2, 3, 4, 5]

# 不可广播的例子
x = paddle.ones((2, 3, 4))
y = paddle.ones((2, 3, 6))
# 此时 x 和 y 是不可广播的，因为第一次比较：4 不等于 6
# z = x + y
# ValueError: (InvalidArgument) Broadcast dimension mismatch.

在了解两个 Tensor 在什么情况下可以广播的规则后，两个 Tensor 进行广播后的结果 Tensor 的形状计算规则如下：

如果两个 Tensor 的形状的长度不一致，会在较小长度的形状矩阵前部添加 1，直到两个 Tensor 的形状长度相等。
保证两个 Tensor 形状相等之后，每个维度上的结果维度就是当前维度上的较大值。

举例如下：

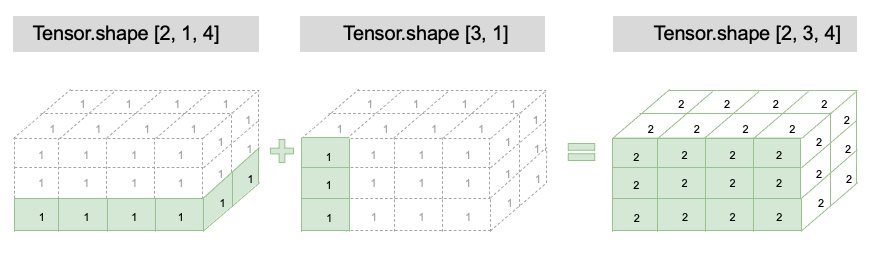
x = paddle.ones((2, 1, 4))
y = paddle.ones((3, 1)) # y 的形状长度为 2，小于 x 的形状长度 3，因此会在 y 的形状前部添加 1，结果就是 y 的形状变为[1, 3, 1]
z = x + y
print(z.shape)
# z 的形状: [2,3,4]，z 的每一维度上的尺寸，将取 x 和 y 对应维度上尺寸的较大值，如第 0 维 x 的尺寸为 2，y 的尺寸为 1，则 z 的第 0 维尺寸为 2

图 3 Tensor 广播示例

六、Tensor 与 Numpy 数组相互转换

如果你已熟悉 Numpy，通过以下要点，可以方便地理解和迁移到 Tensor 的使用上：

Tensor 的很多基础操作 API 和 Numpy 在功能、用法上基本保持一致。如前文中介绍的指定数据、形状、区间创建 Tensor，Tensor 的形状、数据类型属性，Tensor 的各种操作，以及 Tensor 的广播，可以很方便地在 Numpy 中找到相似操作。
但是，Tensor 也有一些独有的属性和操作，而 Numpy 中没有对应概念或功能，这是为了更好地支持深度学习任务。如前文中介绍的通过图像、文本等原始数据手动或自动创建 Tensor 的功能，能够更便捷地处理数据，Tensor 的设备位置属性，可以很方便地将 Tensor 迁移到 GPU 或各种 AI 加速硬件上，Tensor 的 stop_gradient 属性，也是 Tensor 独有的，以便更好地支持深度学习任务。

如果已有 Numpy 数组，可使用 paddle.to_tensor 创建任意维度的 Tensor，创建的 Tensor 与原 Numpy 数组具有相同的形状与数据类型。

tensor_temp = paddle.to_tensor(np.array([1.0, 2.0]))
print(tensor_temp)

Tensor(shape=[2], dtype=float64, place=Place(gpu:0), stop_gradient=True,
       [1., 2.])

注意：

基于 Numpy 数组创建 Tensor 时，飞桨是通过拷贝方式创建，与原始数据不共享内存。

相对应地，飞桨也支持将 Tensor 转换为 Numpy 数组，可通过 Tensor.numpy 方法实现。

tensor_to_convert = paddle.to_tensor([1.,2.])
tensor_to_convert.numpy()

array([1., 2.], dtype=float32)

飞桨 Tensor 介绍

Tensor 介绍

一、Tensor 的概念介绍

二、Tensor 的创建

2.1 指定数据创建

2.2 指定形状创建

2.3 指定区间创建

2.4 指定图像、文本数据创建

2.5 自动创建 Tensor 的功能介绍

三、Tensor 的属性

3.1 Tensor 的形状（shape）

3.2 Tensor 的数据类型（dtype）

3.3 Tensor 的设备位置（place）

3.4 Tensor 的名称（name）

3.5 Tensor 的 stop_gradient 属性

四、Tensor 的操作

4.1 索引和切片

4.1.1 访问 Tensor

4.1.2 修改 Tensor

4.2 数学运算

4.3 逻辑运算

4.4 线性代数

五、Tensor 的广播机制

六、Tensor 与 Numpy 数组相互转换

相关文章