目录
一。朴素贝叶斯的假设
二。朴素贝叶斯的推导
三。高斯朴素贝叶斯Gaussian Naive Bayes
四。多项分布朴素贝叶斯Multinomial Naive Bayes
五。以文本分类为例
1.分析
2.分解
3.拉普拉斯平滑
4.对朴素贝叶斯的思考
六。总结
七。word2vec
八。GaussianNB, MultinomialNB代码
一。朴素贝叶斯的假设
一个特征出现的概率,与其他特征(条件)独立(特征独立性)
其实是:对于给定分类的条件下,特征独立
每个特征同等重要(特征均衡性)
二。朴素贝叶斯的推导
朴素贝叶斯(Naive Bayes,NB)是基于“特征之间是独立的”这一朴素假设,应用贝叶斯定理的监督学习算法。
对于给定的特征向量,类别y的概率可以根据贝叶斯公式得到:
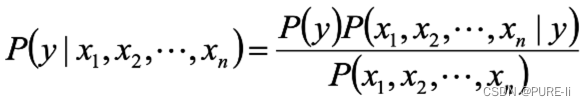
使用朴素的独立性假设:
![]()
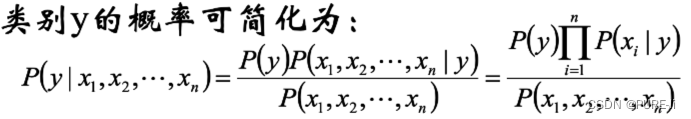
在给定样本的前提下,![]() 是常数:
是常数:
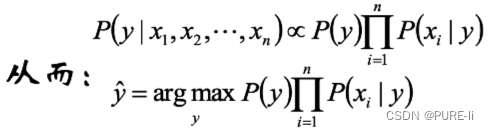
三。高斯朴素贝叶斯Gaussian Naive Bayes
根据样本使用MAP(Maximum A Posteriori)估计 ,建立合理的模型估计 ,从而得到样本的类别。
![]()
假设特征服从高斯分布,即:
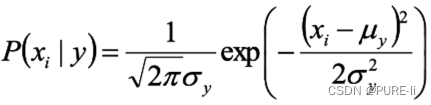
参数使用MLE估计即可。
四。多项分布朴素贝叶斯Multinomial Naive Bayes

五。以文本分类为例
样本:1000封邮件,每个邮件被标记为垃圾邮件或者非垃圾邮件
分类目标:给定第1001封邮件,确定它是垃圾邮件还是非垃圾邮件
方法:朴素贝叶斯
1.分析
类别c:垃圾邮件c1,非垃圾邮件c2
词汇表,两种建立方法:
使用现成的单词词典;
将所有邮件中出现的单词都统计出来,得到词典。
记单词数目为N
将每个邮件m映射成维度为N的向量x
若单词wi在邮件m中出现过,则xi=1,否则,xi=0。即邮件的向量化:m(x1,x2……xN)
贝叶斯公式:P(c|x)=P(x|c)*P(c)/P(x)
P(c1|x)=P(x|c1)*P(c1)/P(x)
P(c2|x)=P(x|c2)*P(c2) / P(x)
注意这里x是向量
2.分解
P(c|x)=P(x|c)*P(c) / P(x)
P(x|c)=P(x1,x2…xN|N|c)=P(x1|c)*P(x2|2|c)…P(xN|N|c)
特征条件独立假设
P(x)=P(x1,x2…xN)N)=P(x1)*P(x2)…P(xN)N)
特征独立假设
带入公式: P(c|x)=P(x|c)*P(c) / P(x)
等式右侧各项的含义:
![]()
P(xi):在所有样本中,单词xi出现的概率
P(cj) :在所有样本中,邮件类别cj出现的概率
3.拉普拉斯平滑

4.对朴素贝叶斯的思考
拉普拉斯平滑能够避免0/0带来的算法异常
要比较的是P(c1|x)和P(c2|x)的相对大小,而根据公式P(c|x)=P(x|c)*P(c)/P(x),二者的分母都是除以P(x),实践时可以不计算该系数。
编程的限制:小数乘积下溢出怎么办?
问题:一个词在样本中出现多次,和一个词在样本中出现一次,形成的词向量相同
由0/1向量改成频数向量或TF-IDF向量
如何判断两个文档的距离
夹角余弦
如何给定合适的超参数![]()
交叉验证
六。总结
在每个时刻,物体的当前可能区域是上一时刻所有可能区域和相应转移概率的乘积和,这恰好是矩阵乘法(矩阵和向量乘法)的定义。
当前可能区域只和上一个时刻的区域有关,而与更上一个时刻无关,因此,是马尔科夫模型。
思考:可以使用“漂流位置”建立马尔科夫模型,该可能位置是不可观察的,而将“转移位置”认为是“漂流位置”的转换结果,“转移位置”是残骸的最终真实位置,使用增强的隐马尔科夫模型。
不要过多累加模型的复杂度,适时使用奥卡姆剃刀(Occam‘sRazor)。
七。word2vec
Word2vec本质是建立了3层神经网络,将所有词都映射为一定长度(如200)的向量;取一定的窗口范围作为当前词的邻域,估计窗口内的词。
词潜入
八。GaussianNB, MultinomialNB代码
priors = np.array((1,2,4), dtype=float)
priors /= priors.sum()
gnb = Pipeline([
('sc', StandardScaler()),#数据进行归一化和标准化
('poly', PolynomialFeatures(degree=1)),#多项式特征
('clf', GaussianNB(priors=priors))]) # 由于鸢尾花数据是样本均衡的,其实不需要设置先验值,高斯分布下的朴素贝叶斯
# gnb = KNeighborsClassifier(n_neighbors=3).fit(x, y.ravel())
gnb.fit(x, y.ravel())
y_hat = gnb.predict(x)
print ('训练集准确度: %.2f%%' % (100 * accuracy_score(y, y_hat)))
y_test_hat = gnb.predict(x_test)
print ('测试集准确度:%.2f%%' % (100 * accuracy_score(y_test, y_test_hat))) # 画图