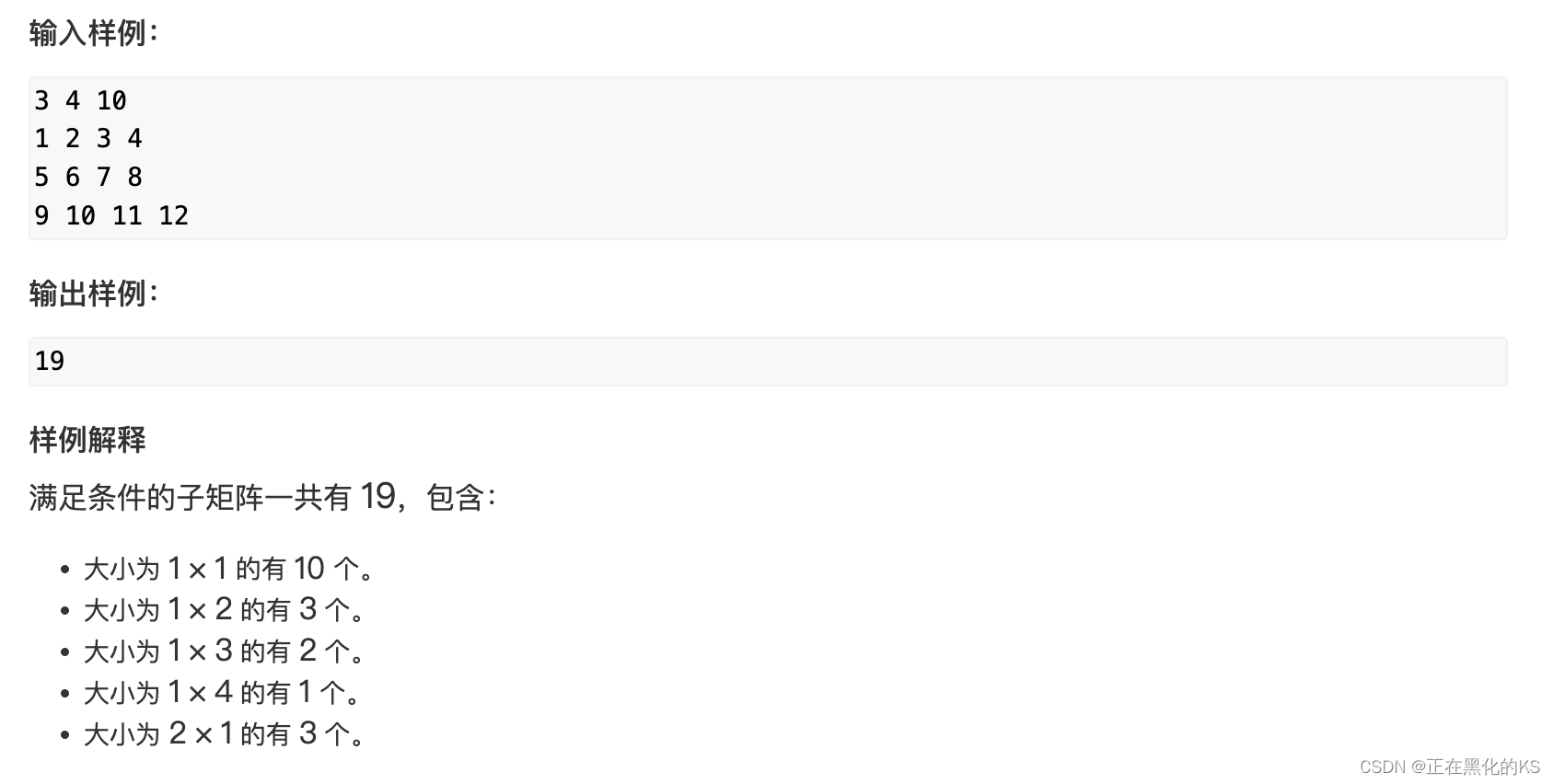
前言：

这道题目是矩阵类型题目经典题型，解题大体思路是前缀和+双指针扫描，在我这篇博客中

第十三届蓝桥杯省赛C++B组题解_第十三届蓝桥杯b组c++答案_正在黑化的KS的博客-CSDN博客

简单提了一下大致解法，今天刷题时又遇到了一个极其相似的题型，所以写下这篇题解巩固加深记忆。

题目描述 

 

 

朴素解法 

朴素解法其实很简单，其实就是二维前缀和后暴力枚举长和宽，时间复杂度是O()，就这个题目的数据范围而言，不能接受，当然也是可以骗点分的，具体代码很简单，这里就不赘述了。

AC解法 

首先，我们这里依然要使用前缀和的技巧，不过这里的前缀和是每列的前缀和，举个例子

g[i][j] 代表的意思是在第j列，第1行到第i行的值。 

现在我们枚举上边界和下边界，即当前枚举矩阵是处在第x行(上边界)，和y(下边界)之间的。

接着枚举矩形的右端点，我们可以发现，每次当右端点向右移动的时候，矩形的面积是单调递增的，此时如果矩形的面积大于K，则不合要求，固定右端点，此时我们将当前矩形的左端点也向右移动，矩形的面积单调变小，直到举行面积再次小于K，停止移动。

那么我们怎么记录答案呢，可以发现每次移动右端点，再配合移动左端点，达到最终状态后，对于当前上下边界及左右边界的矩形而言，这次移动右端点所带来的贡献应该是 

右端点 - 左端点 + 1

因为对于现在这个右端点，向左看，从自身到右端点之间形成的矩形都是面积小于K的，因此贡献应该是左右端点之间的距离，几上面的式子

累加答案即位最终结果

代码 

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std ; 

typedef long long LL ; 

const int N = 510 ; 
int n, m, k ; 
int g[N][N] ;

int main() 
{
    ios::sync_with_stdio(false) ; 
    cin >> n >> m >> k ; 
    for (int i = 1 ; i <= n ; i ++ ) 
        for (int j = 1 ; j <= m ; j ++ )
        {
            cin >> g[i][j] ; 
            g[i][j] += g[i - 1][j] ; // 按列前缀和
        }
        
    LL res = 0 ;
    for (int x = 1 ; x <= n ; x ++ ) // 枚举上界
        for (int y = x ; y <= n ; y ++ ) // 枚举下界
            for (int i = 1, j = 1, sum = 0 ; i <= m ; i ++ ) // i为右端点，j为左端点
            {
                sum += g[y][i] - g[x - 1][i] ; 
                while (sum > k && j < i) 
                {
                    sum -= g[y][j] - g[x - 1][j] ; 
                    j ++ ; 
                }
                
                if (sum <= k) res += i - j + 1 ;
            }
            
    cout << res << endl ;

    return 0 ; 
}

最后附送大家一个相似的练习题

 3487. 最小面积子矩阵 - AcWing题库

这里给出我的AC代码以供参考，思路很类似。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std ; 

const int N = 110, INF = 1e4 + 10 ; 
int g[N][N] ; 
int n, m, k ; 


int main() 
{
    ios::sync_with_stdio(false) ; 
    cin >> n >> m >> k ; 
    for (int i = 1 ; i <= n ; i ++ ) 
        for (int j = 1 ; j <= m ; j ++ ) 
        {
            cin >> g[i][j] ; 
            g[i][j] += g[i - 1][j] ;
        }
        
    int res = INF ; 
    for (int x = 1 ; x <= n ; x ++ ) 
        for (int y = x ; y <= n ; y ++ ) 
            for (int i = 1, j = 1, sum = 0 ; i <= m ; i ++ ) 
            {
                sum += g[y][i] - g[x - 1][i] ; 
                while (sum - g[y][j] + g[x - 1][j] >= k) 
                {
                    sum -= g[y][j] - g[x - 1][j] ; 
                    j ++ ; 
                }
                if (sum >= k) res = min(res, (y - x + 1) * (i - j + 1)) ;
            }
            
    if (res == INF) cout << -1 << endl ; 
    else cout << res << endl ;
    
    return 0 ; 
}