🍎 博客主页：🌙@披星戴月的贾维斯
🍎 欢迎关注：👍点赞🍃收藏🔥留言
🍇系列专栏：🌙 蓝桥杯
🌙我与杀戮之中绽放，亦如黎明的花朵🌙
🍉一起加油，去追寻、去成为更好的自己！
蓝桥杯倒计时 44天

提示：以下是本篇文章正文内容，下面案例可供参考

---

🍎、差分

🍉、差分的简单概念
    差分在数学领域的理解：有数列a1 a2 a3……an……，其中an+1= an + d（ n = 1,2,…n ）d为常数，称为公差， 即 d = an+1 -an , 这就是一个差分, 通常用D(an) = an+1- an来表示，于是有D(an)= d , 这是一个最简单形式的差分方程。
    差分在计算机领域的理解：差分是前缀和的逆运算，差分的作用是在O(1)的时间复杂度下，让一段区间，例如是[i, n]区间内的每一个数都加或者减同一个数。

    一维差分的公式：s[L] += c , s[R + 1] -= c;
其中L是区间的左端点，R是区间的右端点。
    二维差分的公式：S[x1][y2] += c;   s[x1][y2 + 1] -= c;
                                 S[x2 + 1] -= c;   s[x2 + 1][y2 + 1] += c;

    对于差分数组的理解：原数组a[]是差分数组b[]的前缀和，a[i] = b[0] + b[1] + b[2] + … + b[i],所以在最后输出结果时一维差分公式：a[i] = a[i - 1] + b[i];
二维差分最后输出结果的公式是: a[i][j] = a[i - 1][j] + a[i][j - 1] + b[i][j]

🍉、图解一维前缀和

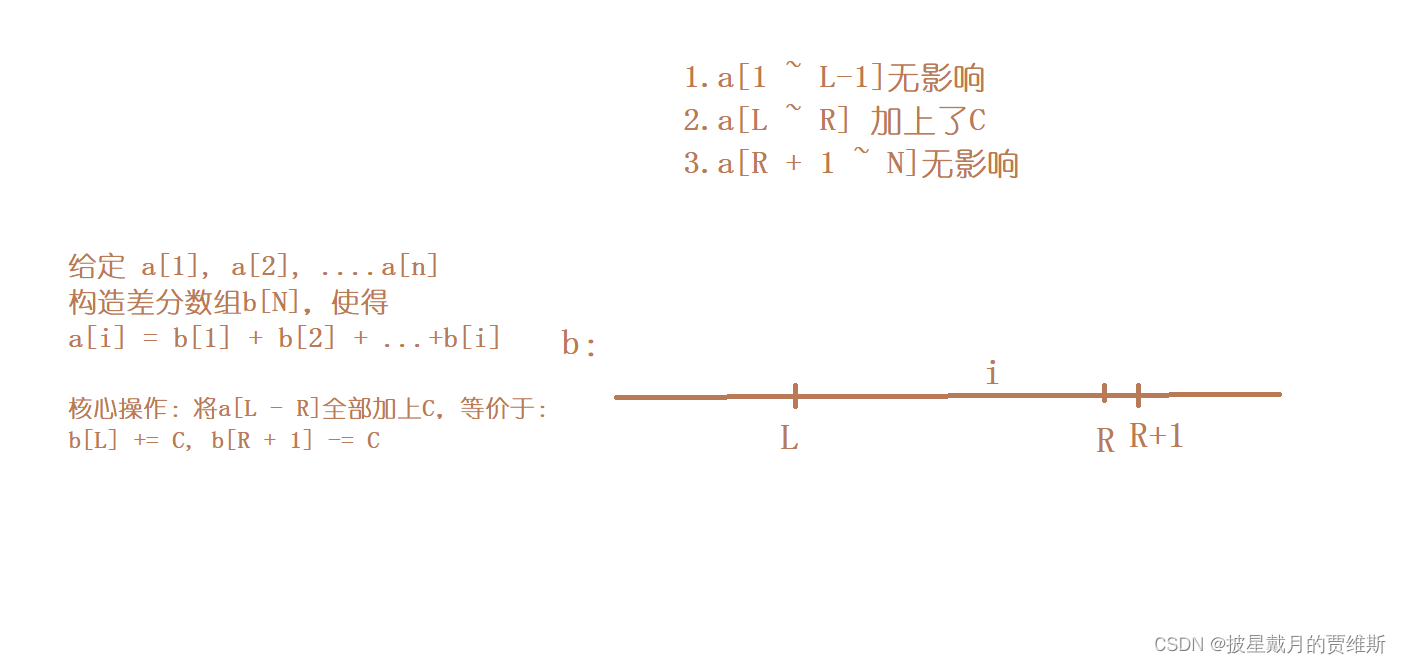
🍉、图解二维前缀和

---

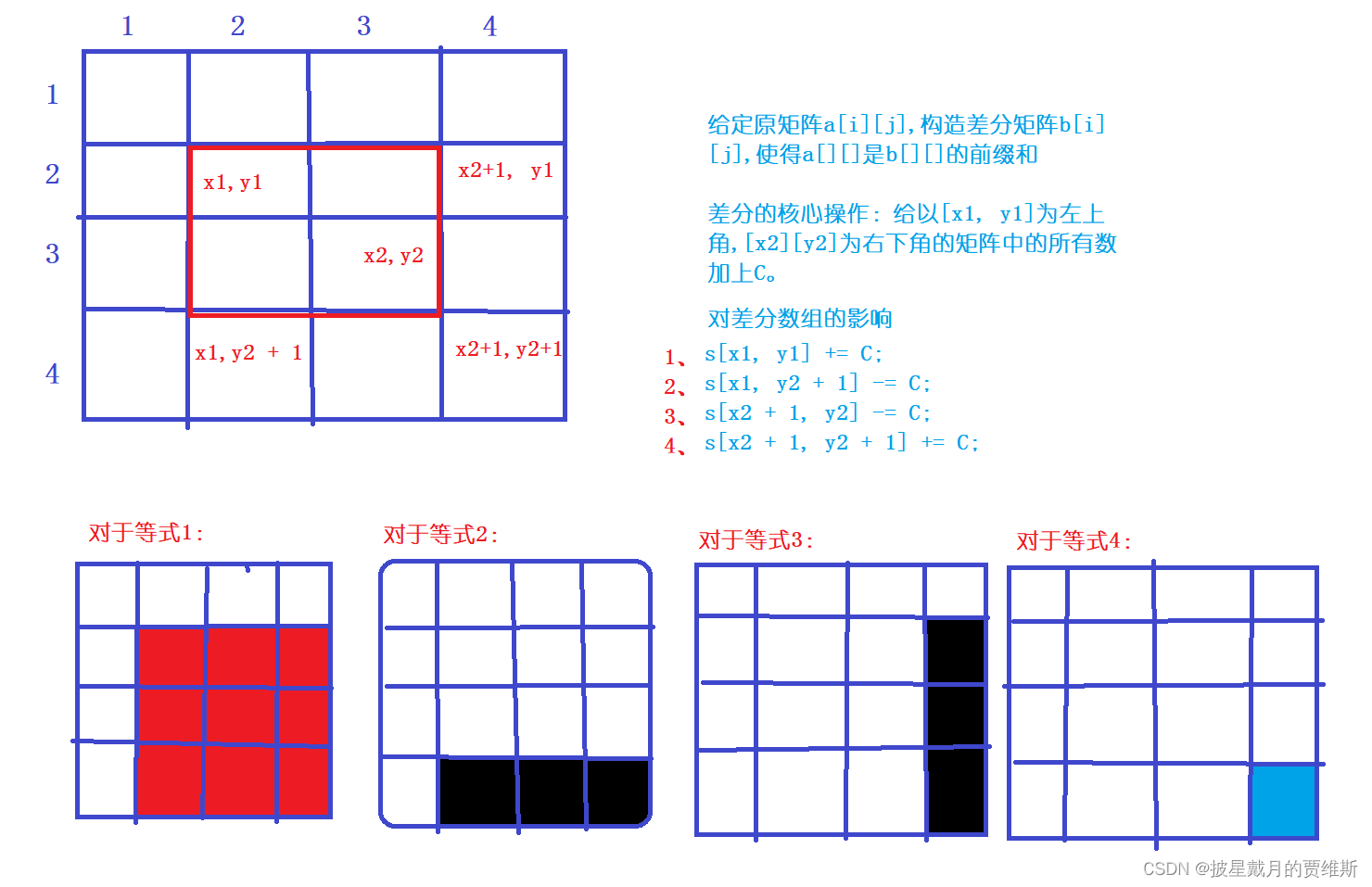
🍎、例题分析

🍇、（AcWing）差分

本题链接: 差分

简单分析题意：就是在q次询问中，每次在原数组的一段区间上加上一个值C，最后输出q次询问后的结果。
代码示例：

#include<iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];
void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}
int main ()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> a[i];
        insert(i, i, a[i]);//对b[i]的初始化
    }
    while(m --)
    {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l, r, c);
    }
    for(int i = 1; i <= n; i++)
    {
        a[i] = a[i - 1] + b[i];
        cout << a[i] << ' ';
    }
    cout << endl;
    return 0;
}

🍇、（AcWing）差分矩阵

本题链接: 差分矩阵

简单分析题意：就是在q次查询中，每次在一个区间内加/减一个值。
代码示例：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int b[N][N], a[N][N];
int n, m, q;
void add(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main ()
{
    cin >> n >> m >> q;
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
        {
            scanf("%d", &a[i][j]);
            add(i, j, i, j, a[i][j]); // 每次输入一个a[i],就要初始化一下b差分数组
        }
    while(q --)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        add(x1, y1, x2, y2, c);
    }
    for(int i = 1; i <=n;  i++)
    {
        for(int j = 1; j <= m; j++)
        {
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];//这里使用二维前缀和公式
            printf("%d ", a[i][j]);
        }
        puts("");
    }
    
    return 0;
}

🍇、（AcWing）改变数组元素

本题链接: 改变数组元素

分析题意：

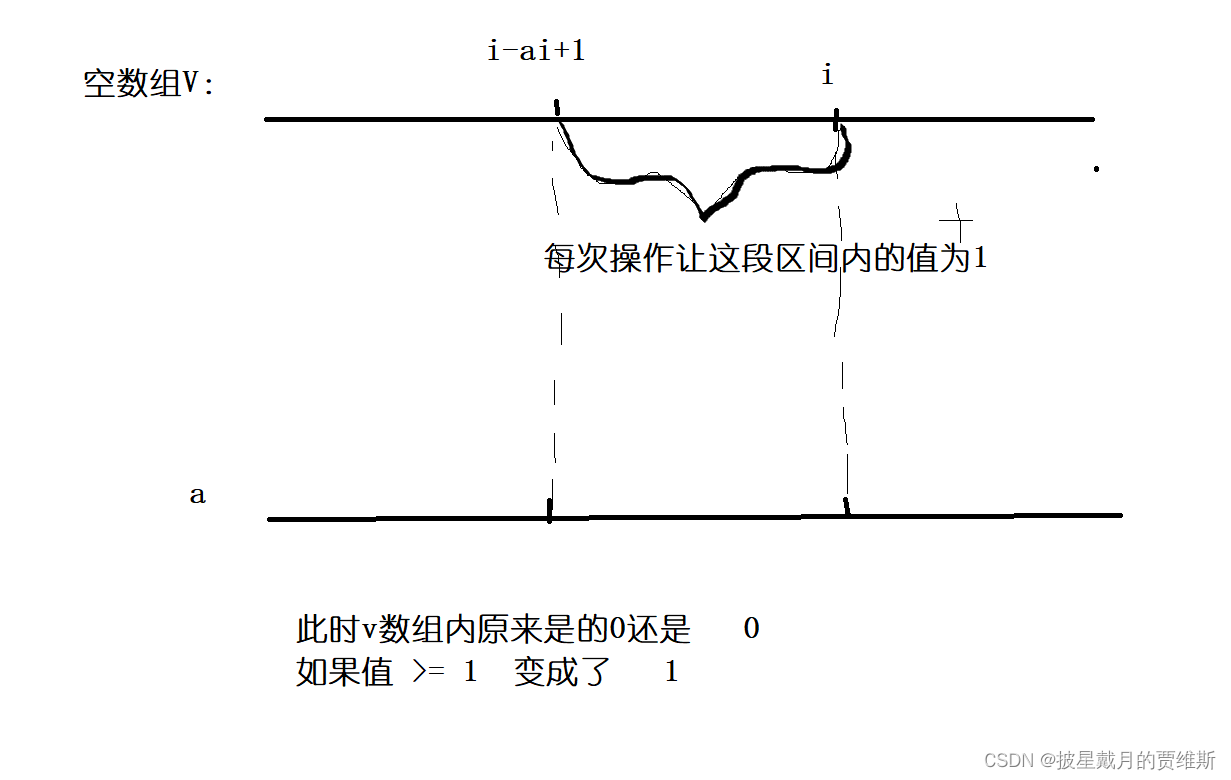
代码示例：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 200010;
int b[N];
int n;
int main ()
{
    int t;
    cin >> t;
    
    while(t --)
    {
        scanf("%d", &n);
        memset(b, 0, 4 * (n + 1));
        for(int i = 1; i <= n; i++)
        {
            int x;
            scanf("%d", &x);
            x = min(x, i);
            int l = i - x + 1, r = i;//差分数组的左右两端
            b[l]++, b[r + 1]--; //差分操作的模板
        }    
        //求原数组，就是差分数组的前缀和
        for(int i = 1; i <= n; i++)
        {
            b[i] += b[i - 1]; //差分和前缀和是互逆操作
        }
        for(int i = 1; i <= n; i++)
        printf("%d ", !!b[i]); // 原来是0的还是0，原来大于等于1的就变为1了。
        puts("");
    }
    
    return 0;
}

🍎、总结

    本文简要介绍了差分的简要概念和几道差分的经典例题，希望大家读后能有所收获！