1. 双指针

双指针算法的核心思想：将暴力解法的时间复杂度，通常是O(N*N)，通过某种特殊的性质优化到O(N)。

做题思路：先想想暴力解法的思路，然后分析这道题的特殊性质，一般是单调性。然后得出双指针算法的思路。

双指针算法的模板：

for(int i = 0; i <ｎ; i++)

{

while(j < i && check(i, j))

j++;

//具体题目的解题思路

}、

1.1 例题

给定一个长度为 n 的整数序列，请找出最长的不包含重复数数字的最长子序列，输出它的长度。

输入格式

第一行包含整数 n 。

第二行包含 n 个整数（均在0 ~ 100000范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复数字的连续子序列的长度。

数据范围

1 <= n <= 100000

按照上面介绍的解题思路：我们先看看暴力解法怎么做的：两层for循环，外层循环在遍历数组时，对于外层循环遍历的每一个值，内层循环都会从该位置开始去遍历，通过检查区间内是否存在重复数字，更新结果。显然这种解法的事件复杂度为O(N*N)。伪代码如下：

for (int i = 0; i < n; i++)
{
   for (j = i + 1; j < n; j++)
   {
if (!check(i, j))
           ret = max(ret, i - j + 1);
   }
}

其中n为数组的长度，check为检查区间 [ i, j ] 中的元素是否存在重复的数字，如果不存在更新结果，保存到ret中。

双指针：同样根据上面提供的解题思路，我们尝试从暴力解法中分析出单调性。嗯，双指针的左侧指针在整个查找过程中是单调的。怎么理解呢？

下面以一个具体的例子：1,2,2,3,5 来分析哈：

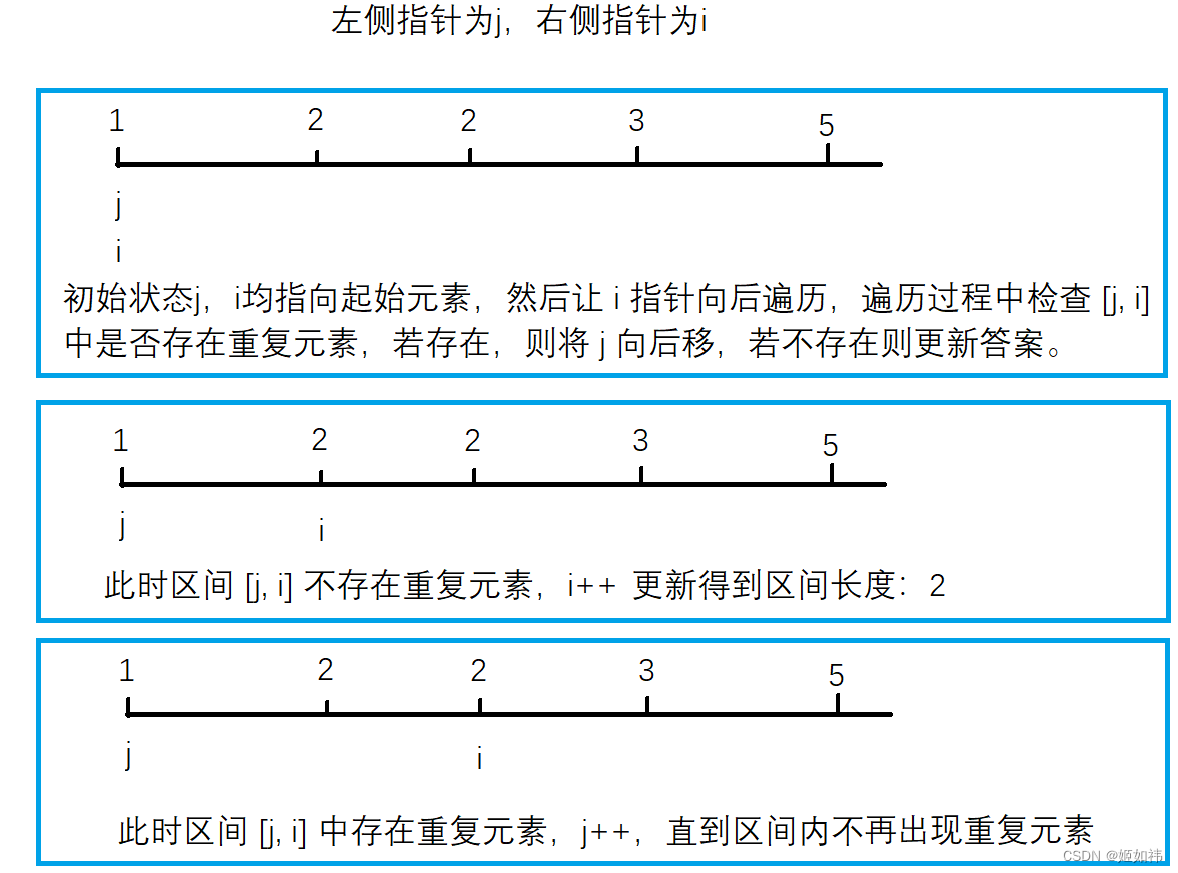
现在我们已经知道了双指针的大致思路了，但是好像还没有弄清除单调性从何而来。对于本题单调性就是：在 i++ 向右找更大的满足要求的更长区间时，j不可能存在向前动 (j--) 的情况。即，本题中 j 具有单调性。

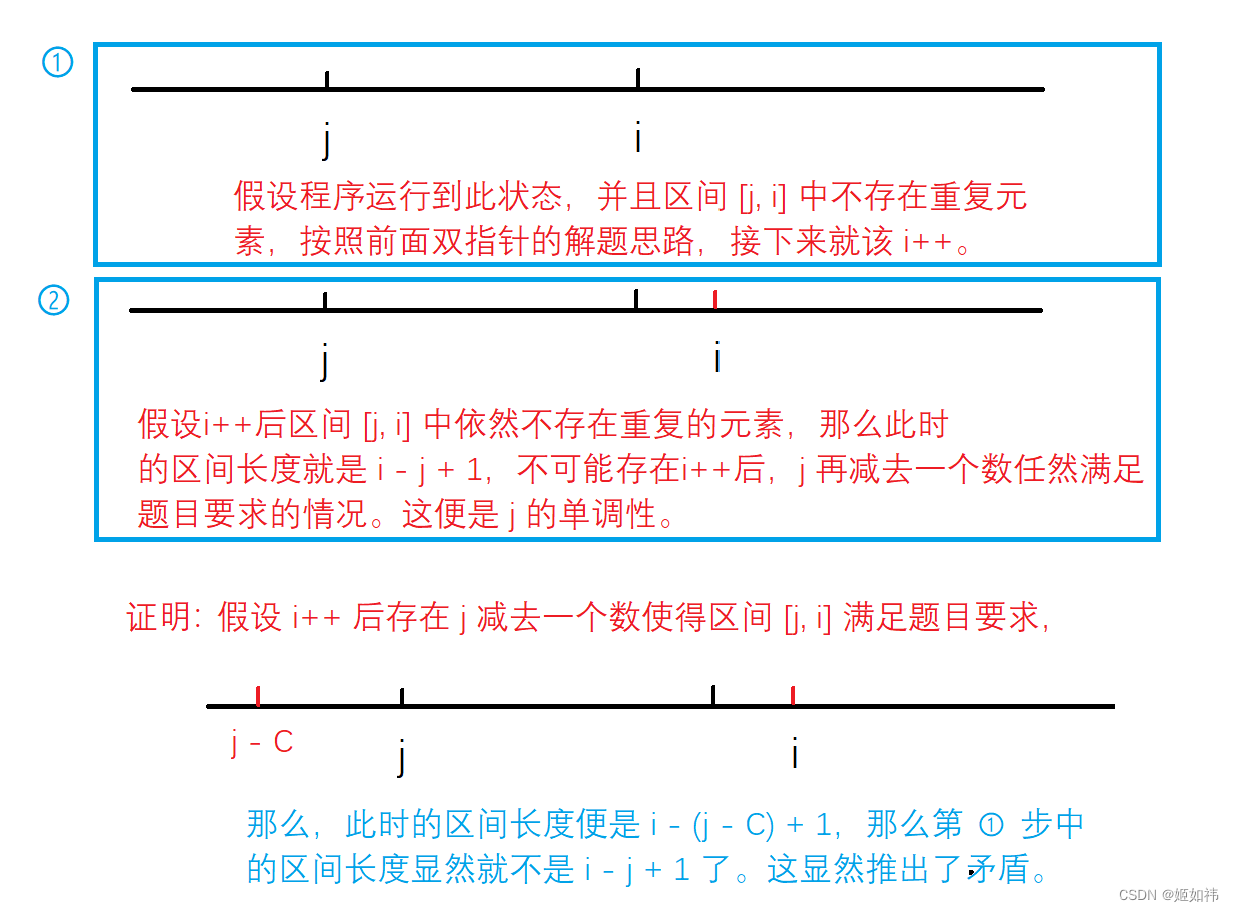
弄清除了这些，我们只需要知到怎么判定一个区间中是否有重复元素就行了。我们可以初始化一个数组a，遍历原数组b, 得到的值假设为s，就让 a[s] + 1，代表这个数字出现了一次。注意当一个区间中没有重复元素时，i++，那么只有原数组中下标为 i 的的值才会是重复的元素，因此我们只需要判断 a[b[i]] 的值是否是大于 1 即可。这就是模板中的 check 。另外本题中不要 i > j 这个条件，因为 i == j 时，区间 [j, i] 中就没有重复的元素了，i然后就会加一，即 j 是不会大于 i 的。

当区间内存在重复元素时，j++的同时要将 a[b[j]]--，少了一个数字嘛。

现在可以写代码啦！

int main()
{
	const int N = 100000;

	//原数组
	int b[N];
	//统计数字出现次数的数组
	int a[N] = { 0 };

	//用于保存最大的区间长度
	int ret = 0;
	int j = 0;

	//读入数据
	int n;
	scanf("%d", &n);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &b[i]);
	}

	//核心算法
	for (int i = 0; i < n; i++)
	{
		a[b[i]]++;
		while (a[b[i]] > 1)
		{
			//少一个数字，次数减一
			a[b[j]]--;
			j++;
		}
		//更新结果
		ret = ret > i - j + 1 ? ret : i - j + 1;
	}
	//打印结果
	printf("%d\n", ret);

	system("pause");
	return 0;
}