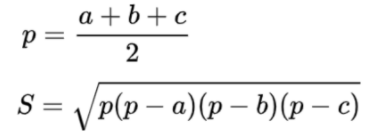计算几何原理与例题

news2025/1/19 11:10:26

目录

一、前言

二、简单几何

1、平面切分（2020年省赛，lanqiaoOJ题号503）

2、三角形的面积（lanqiaoOJ题号1231）

3、点和直线关系（lanqiao0J题号1240）

4、点和线段关系（lanqiaoOJ题号1242）

5、点到直线距离（lanqiaoOJ题号1286）

三、凸包

1、求土包子（lanqiaoOJ题号1316）

一、前言

本文主要讲了简单几何概念（平面切分、三角形面积、点与直线、点与线段、凸包）和相关例题。

二、简单几何

1、平面切分（2020年省赛，lanqiaoOJ题号503）

【题目描述】

平面上有 N 条直线，其中第 i 条直线是 y=(Ai)x+Bi。请计算这些直线将平面分成了几个部分。

【输入描述】

第一行包含一个整数 N。以下 N 行，每行包含两个整数 Ai, Bi。

【输出描述】

一个整数代表答案。

对于50%的评测用例，1<=N<=4，-10≤A, B≤10。

对于所有评测用例，1<=N<=1000，-100000<=A, B<=100000。

【思路】

  • 先看第一条和第二条线。第一条线把平面分成 2 半，第二条线如果与第一条平行，把平面分成 3 部分；如果不平行，有 1 个交点，把平面分成 4 部分。
  • 总结：每增加一条直线，平面分割的增加数量，等于 “其与先前直线的交点数（不包括与已有交点重合的点）+ 1” 。
  • 首先对输入的直线去重，然后按上述规则统计平面被直线分成了几个部分。每加入一条直线，暴力计算它与其他直线的交点即可。
n=int(input())
line=[tuple(map(int,input().split())) for i in range(n)]
se=set(line)
line=list(se)       #去重后的线
ans=2
for i in range(1,len(line)):    #从第二条直线开始
    a1,b1=line[i]
    pos=set()       #存交点
    for j in range(i):          #第1条直线与第1~i-1条直线的关系
        a2,b2=line[j]
        if a1==a2:            #平行，无交点
            continue
        x=(b2-b1)/(a1-a2)
        y=a1*x+b1
        poss.add((x,y))
    ans+=len(pos)+1
print(ans)

2、三角形的面积（lanqiaoOJ题号1231）

【题目描述】

平面直角坐标系中有一个三角形，请你求出它的面积。

【输入描述】

第一行输入一个T，代表测试次数。每组测试输入有三行，每行一个坐标 (x， y) 代表三个点。1<=T<=10^3，-10^5<=x,y<=10^5。

【输出描述】

输出一个实数表示三角形面积。

用海伦公式编码，Python 代码会有较大误差。

from math import *
def Dist(x1,y1,x2,y2):
    return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))
t=int(input())
for i in range(t):
    x1,y1=map(float,input().split())
    x2,y2=map(float,input().split())
    x3,y3=map(float,input().split())
    a=Dist(x1,y1,x2,y2)
    b=Dist(x1,y1,x3,y3)
    c=Dist(x2,y2,x3,y3)
    p=(a+b+c)/2
    s=sqrt(p*(p-a)*(p-b)*(p-c))
    print("{:.2f}".format(s))

本题的正解是用叉积求面积。

【点和向量】

二维平面中的点用坐标 (x, y) 来表示。计算几何的基础是向量。有大小有方向的量，称为向量。只有大小而没有方向的量，称为标量。

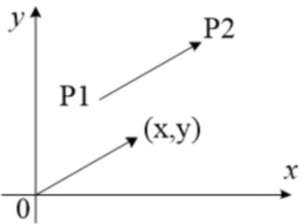
用平面上的两个点可以确定一个向量，例如用起点 P1 和终点 P2 表示一个向量。·为了简化描述，可以把它平移到原点，把向量看成从原点 (0, 0) 指向点 (x,y) 的一个有向线段。向量的表示，在形式上与点的表示完全一样。

【向量的计算】

1）加：点与点的加法运算没有意义；点与向量相加得到另一个点；向量与向量相加得到另外一个向量。

2）减：两个点的差是一个向量；向量A减B，得到由B指向A的向量。

3）乘：向量与实数相乘得到等比例放大的向量。

4）除：向量与实数相除得到等比例缩小的向量。

【点积】

点积 (Dot product)：记向量 A 和 B 的点积为 A+B

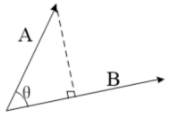
定义：A+B=|A||B|cosθ，其中 θ 为A、B之间的夹角。

点积的几何意义为 A 在 B 上的投影长度乘以 B 的模长。

编程时计算点积，并不需要知道 θ。如果已知 A=(A.x, A.y)，B=(B.x, B.y)，有：

A·B = A.x*B.x + A.y*B.y

【点积的应用】

1）判断 A 与 B 的夹角是钝角还是锐角

点积有正负，利用正负号，可以判断向量的夹角：

若 dot(A, B)>0，A 与 B 的夹角为锐角；

若 dot(A, B)<0，A 与 B 的夹角为钝角；

若 dot(A, B)=0，A 与 B 的夹角为直角。

【叉积】

叉积：AXB=|A||B|sinθ

θ 表示向量 A 旋转到向量 B 所经过的夹角。

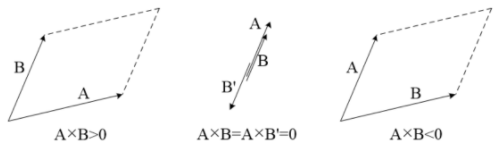
两个向量的叉积是一个带正负号的数值。AXB 的几何意义为向量 A 和 B 形成的平行四边形的“有向”面积，这个面积有正负。

向量 A、B 的叉积 AXB：A.x*B.y-A.y*B.x

【叉积的应用】

1）判断向量 A、B 的方向关系

若 AXB>0，B 在 A 的逆时针方向；

若 AXB<0，B 在 A 的顺时针方向；

若 AXB=0，B 与 A 共线，可能是同方向的，也可能是反方向的。

2）计算两向量构成的平行四边形有向面积

三个点 A、B、C，以 A 为公共点，得到 2 个向量 B-A 和 C-A，它们构成的平行四边形，面积是：Cross(B-A, C-A)；

如果以 B 或 C 为公共点构成平行四边形，面积是相等的，但是正负不一样。

3）计算三点构成的三角形的面积。三个点 A、B、C 构成的三角形面积，等于平行四边形面积的二分之一。

好了，扯了这么多，我们再回顾一下题目。

接下来用叉积求面积。

def Cross(x1,y1,x2,y2):     #叉积
    return x1*y2-y1*x2
t=int(input())
for i in range(t):
    x1,y1=map(float,input().split())
    x2,y2=map(float,input().split())
    x3,y3=map(float,input().split())
    a1=x1-x2
    a2=y1-y2
    b1=x1-x3
    b2=y1-y3
    s=Cross(a1,a2,b1,b2)/2    #用叉积算面积
    if s<0:
        s=-s                #取绝对值
    print("{:.2f}".format(s))   #或者：print("%.2f"%s)

3、点和直线关系（lanqiao0J题号1240）

【题目描述】

平面直角坐标系中有一个点 C 和一条直线 AB，求点 C 和直线 AB 的位置关系。

【输入描述】

第 1 行是整数 T，表示测试数量。每组测试输入三行，每行一个坐标 (x, y) 分别代表 A、B、C 三点。

【输出描述】

如果点 C 在直线 AB 上，输出 IN，如果点 C 在直线 AB 左侧，输出 L，如果点 C 在直线 AB 右侧输出 R。

【点和直线关系】

二维平面上，点和直线有三种位置关系：点在直线左侧、在右侧、在直线上。

用直线上的两点 p1 和 p2，与点 p 构成两个向量，用叉积的正负判断方向，就能得到位置关系。

也可以用 p、p1、p2 三点形成的三角形的面积来确定 p 和直线 p1p2 的关系。

设直线上两个点是 A、B，判断的点为 C。

S(A, B, C) 是三个点围成的三角形面积。

如果 S(A，B，C) 为正数，则 C 在直线 AB 的左侧；

如果 S(A，B，C) 为负数，则 C 在直线 AB 的右侧；

如果 S(A，B，C) 为 0，则 C 在直线 AB 上。

def Cross(x1,y1,x2,y2):         #叉积
    return x1*y2-y1*x2
t=int(input())
for _ in range(t):
    ax,ay=map(float,input().split())
    bx,by=map(float,input().split())
    cx,cy=map(float,input().split())
    x1=ax-bx
    y1=ay-by
    x2=ax-cx
    y2=ay-cy
    s=Cross(x1,y1,x2,y2)/2      #用叉积算面积
    if s>0:
        print("L")
    if s<0:
        print("R")
    if s==0:
        print("IN")

4、点和线段关系（lanqiaoOJ题号1242）

【题目描述】

平面直角坐标系中有一个点 C 和一条线段 AB，求点 C 和线段 AB 的位置关系。

【输入描述】

第 1 行是整数 T，表示测试数量。每组测试输入三行，每行一个坐标 (x, y) 分别代表 A、B、C 三点。

【输出描述】

如果点 C 在线段AB上，输出 Yes，否则输出 No。

【点和线段的关系】

判断点 p 是否在线段 v 上：

先用叉积判断是否共线；

然后用点积看 p 和 v 的两个端点产生的角是否是钝角 (实际上应该是180度角)。

def Cross(x1,y1,x2,y2):         #叉积
    return x1*y2-y1*x2
def Dot(x1,y1,x2,y2):
    return x1*x2+y1*y2          #点积
t=int(input())
for _ in range(t):
    ax,ay=map(float,input().split())
    bx,by=map(float,input().split())
    cx,cy=map(float,input().split())
    x1=ax-bx
    y1=ay-by
    x2=ax-cx
    y2=ay-cy
    if Cross(x1,y1,x2,y2)==0 and Dot(x1,y1,x2,y2)>=0:
        print('Yes')
    else:
        print('No')

5、点到直线距离（lanqiaoOJ题号1286）

【题目描述】

平面直角坐标系中有一个点 C 和一条线段 AB，求点 C 到直线 AB 的距离。

【输入描述】

第 1 行是整数 T，表示测试数量。每组测试输入三行，每行一个坐标 (x, y) 分别代表 A、B、C 三点。

【输出描述】

输出一个实数表示距离。结果保留 2 位小数。

已知点 p 和直线 v(p1,p2)，求 p 到 v 的距离。

首先用叉积求 p、p1、p2 构成的平行四边形面积，然后用面积除以平行四边形的底边长，也就是线段 (p1, p2) 的长度，就得到了平行四边形的高，即 p 点到直线的距离。

from math import *
def Cross(x1,y1,x2,y2):
    return x1*y2-y1*x2      #叉积
t=int(input())
for i in range(t):
    ax,ay=map(float,input().split())
    bx,by=map(float,input().split())
    cx,cy=map(float,input().split())
    d=abs(Cross(ax-cx,ay-cy,bx-cx,by-cy))   #用叉积算面积
    w=sqrt((ax-bx)*(ax-bx)+(ay-by)*(ay-by))
    print("%.2f"%(d/w))

三、凸包

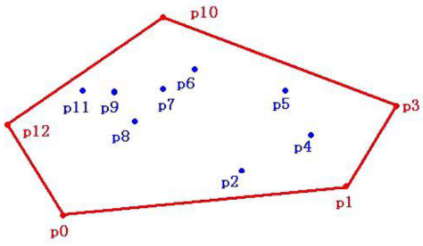
凸包问题：给定一些点，求能把所有这些点包含在内的面积最小的多边形。

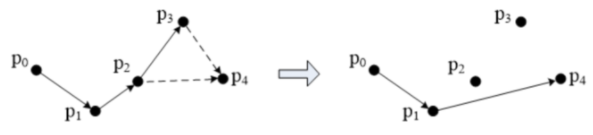
Andrew 算法：两次扫描，先从最左边的点沿 “下凸包” 扫描到最右边，再从最右边的点沿 “上凸包” 扫描到最左边，“上凸包” 和 “下凸包” 合起来就是完整的凸包。

 1）把所有点按照横坐标 x 从小到大进行排序，如果 x 相同，按 y 从小到大排序。得到序列 {p0, p1, p2, ..., pm}。

2）从左到右扫描所有点，求 “下凸包”。p0 一定在凸包上，它是凸包的最左边的顶点，从 p0 开始，依次检查 {p1, p2, ..., pm}，扩展出 “下凸包”。

3）从右到左重新扫描所有点，求 “上凸包”。

1、求土包子（lanqiaoOJ题号1316）

【题目描述】

平面直角坐标系中求一个凸包的周长 C。

【输入描述】

第 1 行是整数 n，接下来输入 n 行，每行一个坐标 (x, y)。n<5×10^4。

【输出描述】

输出一个实数 C，结果保留 6 位小数。

from decimal import *
from math import *

class Point:
    def __init__(self,x=0,y=0):
        self.x=x
        self.y=y
    def __sub__(self,other):
        return Point(self.x-other.x,self.y-other.y)

def cross(a,b):
    return a.x*b.y-b.x*a.y
def square(x):
    return x*x
def dis2(a,b):
    return square(a.x-b.x)+square(a.y-b.y)
def dis(a,b):
    return sqrt(dis2(a,b))

def convex_hull(p):   
    def cmp(a):      #把所有点按照横坐标x从小到大进行排序，如果x相同，按y从小到大排序
        return a.x*Decimal(1e9)+a.y
    p=sorted(p,key=cmp)
    n=len(p)
    stk=[]           #用stk记录凸包上的点
    stk.append(p[0])
    for i in p[1:]:  #从左到右扫描所有点，求“下凸包”
        while len(stk)>1 and cross(stk[-1]-stk[-2],i-stk[-2])<=0:
            del stk[-1]
        stk.append(i)
    tmp=len(stk)
    for i in p[::-1]:  #从右到左重新扫描所有点，求“上凸包”
        while len(stk)>tmp and cross(stk[-1]-stk[-2],i-stk[-2])<=0:
            del stk[-1]
        stk.append(i)
    stk.pop()
    return stk
        
n=int(input())
p=[Point() for i in range(n)]
for i in p:
    i.x,i.y=map(Decimal,input().split())
convex=convex_hull(p)
C=0
for i in range(len(convex)):
    C+=dis(convex[i-1],convex[i])
print("%.6f"%C)

以上，计算几何

祝好

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/364650.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

活动回顾丨研发效能度量线下沙龙圆满举办

活动回顾丨研发效能度量线下沙龙圆满举办

2月18日&#xff0c;由跬智信息&#xff08;Kyligence&#xff09;联合甄知科技主办的研发效能度量线下沙龙圆满举办。本次沙龙在 Kyligence 上海总部举办&#xff0c;Kyligence 联合创始人兼 CTO 李扬、腾讯 Tech Lead 茹炳晟&#xff0c;以及甄知科技创始人兼 CTO 张礼军在现…
阅读更多...
ClickHouse学习笔记（一）：ClickHouse架构概述（为什么ClickHouse这么快呢？）

ClickHouse学习笔记（一）：ClickHouse架构概述（为什么ClickHouse这么快呢？）

文章目录1、ClickHouse 概述1.1 、简述1.2 、名词解释1.2.1 、MPP 架构1.2.2 、向量化执行引擎1.2.3 、SIMD1.2.4 、OLAP1.3、应用场景2、ClickHouse 核心特性2.1、完备的 DBMS 功能2.2、列式存储与数据压缩2.3、向量化执行引擎2.4、关系模型与SQL查询2.5、多样化的表引擎2.6、…
阅读更多...
简单的C++:【运算符重载】新手易学

简单的C++:【运算符重载】新手易学

学过C语言的同志们应该都知道位运算符>> 和 << &#xff08;右移左移&#xff09;&#xff0c;但是这两个运算符在C中还是我们的输入和输出流操作符&#xff0c;那么这是为什么呢&#xff1f;&#xff0c;了解完本篇文章之后&#xff0c;我们再来回答这个问题。 C为…
阅读更多...
python和C++代码实现模拟动态指针时钟

python和C++代码实现模拟动态指针时钟

一、python代码实现及turtle库简单介绍 桌面时钟项目描述 1、使用turtle库绘制时钟外形及表针&#xff1b; 2、使用datetime获取系统时间&#xff1b; 3、时钟动态显示 turtle库基本命令 1、turtle.setup()函数&#xff1a;用于启动一个图形窗口&#xff0c;它有四个参数…
阅读更多...
2023-02-22干活小计

2023-02-22干活小计

复现BERT&#xff1a; 只能说爷今天干了一上午一下午的代码 bert的输入&#xff1a; batch_size * max_len * emb_num 768 * 768 bert的输出&#xff1a;三维字符级别特征(NER可能就更适合) 二维篇章级别特征(比如文本分类可能就更适合) batch_size * max_len * emb_num, ba…
阅读更多...
亲身试验 Outlook防关联方法分享

亲身试验 Outlook防关联方法分享

Outlook在海外的用途是很广泛的&#xff0c;不仅可以用于收发邮件&#xff0c;还可以作为各类第三方网站的登录凭证。所以Microsoft对于Outlook的监管还是比较严格的&#xff0c;跨境卖家大量注册Outlook账号使用的话很容易被检测出关联然后被封号。龙哥针对Outlook防关联的问题…
阅读更多...
35-Golang中的方法

35-Golang中的方法

Golang中的方法方法的介绍和使用方法的声明和调用方法的调用和传参机制原理方法的声明(定义)方法注意事项和细节讨论方法和函数的区别方法的介绍和使用 在某些情况下&#xff0c;我们需要声明(定义)方法。比如person结构体&#xff0c;除了有一些字段外(年龄&#xff0c;姓名……
阅读更多...
unix高级编程-僵尸进程和孤儿进程

unix高级编程-僵尸进程和孤儿进程

僵尸进程&#xff1a; 一个父进程利用fork创建子进程&#xff0c;如果子进程退出&#xff0c;而父进程没有利用wait 或者 waitpid 来获取子进程的状态信息&#xff0c;那么子进程的状态描述符依然保存在系统中。 孤儿进程&#xff1a;一个父进程退出&#xff0c; 而它的一个或…
阅读更多...
java+Selenium+TestNg搭建自动化测试架构(3)实现POM（page+Object+modal）

java+Selenium+TestNg搭建自动化测试架构(3)实现POM（page+Object+modal）

1.Page Object是Selenium自动化测试项目开发实践的最佳设计模式之一&#xff0c;通过对界面元素的封装减少冗余代码&#xff0c;同时在后期维护中&#xff0c;若元素定位发生变化&#xff0c;只需要调整页面元素封装的代码&#xff0c;提高测试用例的可维护性。 PageObject设计…
阅读更多...
软件测试，刚进入一个公司如何快速上手一个项目？

软件测试，刚进入一个公司如何快速上手一个项目？

目录 前言 客观现状 主观能动性 总结感谢每一个认真阅读我文章的人&#xff01;&#xff01;&#xff01; 重点&#xff1a;配套学习资料和视频教学 前言 刚入职一家新公司&#xff0c;做的项目是之前很少接触的行业&#xff0c;该怎么快速的熟悉并上手自己的工作&#xf…
阅读更多...
富文本编辑组件封装，tinymce、tinymce-vue

富文本编辑组件封装，tinymce、tinymce-vue

依赖&#xff1a;package.json yarn add tinymce tinymce/tinymce-vue {"dependencies": {"tinymce/tinymce-vue": "5.0.0","tinymce": "6.3.1","vue": "3.2.45",}, } 本地依赖&#xff1a; 在publ…
阅读更多...
JIT-即时编译技术

JIT-即时编译技术

VM&#xff08;HotSpot&#xff09;执行引擎中包含解释器与JIT编译器热点代码&#xff08;执行多次&#xff09;才有JIT编译的必要&#xff08;JIT编译阈值&#xff09;JVM&#xff08;HotSpot&#xff09;会有两个计数器&#xff08;次数/回边&#xff09;判断方法/代码块是否…
阅读更多...
缺少IT人员的服装行业该如何进行数字化转型？

缺少IT人员的服装行业该如何进行数字化转型？

服装行业上、下游产业链长&#xff0c;产品属性复杂&#xff0c;是劳动密集型和技术密集型紧密结合的产物&#xff0c;是典型的实体经济代表。 近二十年是服装业发展的机遇和挑战之年&#xff0c;从“世界工厂”“中国制造”&#xff0c;逐渐向“中国设计”转变,中国服装产业经…
阅读更多...
Kotlin新手教程九（协程）

Kotlin新手教程九（协程）

一、协程 协程从Kotlin1.3开始引入&#xff0c;本质上协程就是轻量级的线程。协程的基本功能点有&#xff1a; 轻量&#xff1a;可以在单个线程上运行多个协程&#xff0c;因为协程支持挂起&#xff0c;不会使正在运行协程的线程阻塞。挂起比阻塞节省内存&#xff0c;且支持多…
阅读更多...
扬帆优配|雷达供应商Arbe暴涨近50%；A股毫米波雷达概念异军突起

扬帆优配|雷达供应商Arbe暴涨近50%；A股毫米波雷达概念异军突起

今日早盘&#xff0c;A股全体低开高走&#xff0c;上证指数围绕3300点重复抢夺&#xff0c;两市成交呈现大幅萎缩的趋势&#xff0c;显示市场谨慎情绪较为浓厚。 盘面上&#xff0c;白酒、国防军工、新能源、医药等板块涨幅居前&#xff0c;电信运营、网络游戏、稳妥、房地产等…
阅读更多...
Sqoop导出hive/hdfs数据到mysql中---大数据之Apache Sqoop工作笔记006

Sqoop导出hive/hdfs数据到mysql中---大数据之Apache Sqoop工作笔记006

然后我们看看数据利用sqoop,从hdfs hbase中导出到mysql中去 看看命令可以看到上面这个 这里上面还是mysql的部分,然后看看 下面--num-mappers 这个是指定mapper数 然后下面这个export-dir这里是,指定hdfs中导出数据的目录 比如这里指定的是hive的一个表/user/hive/warehouse…
阅读更多...
IOS开发中遇到的问题总结【持续更新】

IOS开发中遇到的问题总结【持续更新】

目录 知识点补给站 1. SwiftUI中的Image控件使用系统图标 知识点补给站 【Swift学习】关于 Swift | Swift 编程语言中文教程&#xff08;The Swift Programming Language&#xff09;【SwiftUI学习】不要惊慌! SwiftUI Example【SwiftUI学习】https://goswiftui.com【AppIcon…
阅读更多...
C#、JAVA读写PLC物联网Modbus

C#、JAVA读写PLC物联网Modbus

Modbus协议是一种常用于工业自动化领域的通信协议&#xff0c;它使用简单、易实现、可靠的特点得到了广泛应用。物联网中的设备也需要使用Modbus协议进行通信。本文将介绍物联网Modbus通信的相关内容。一、Modbus协议简介Modbus协议是一种串行通信协议&#xff0c;它最初由Modi…
阅读更多...
浅谈ThreadLocal的原理

浅谈ThreadLocal的原理

文章目录1.ThreadLocal初识2.ThreadLocal底层原理3.ThreadLocal核心API3.1.get()方法3.2.set()方法3.3.remove()方法3.4.核心代码及流程4.ThreadLocalMap5.Hash冲突怎么解决6.ThreadLocal内存泄漏问题及解决办法7.应用场景8.总结1.ThreadLocal初识 ThreadLocal概念&#xff1a…
阅读更多...
RPC(2)------ Netty(NIO) + 多种序列化协议 + JDK动态代理实现

RPC(2)------ Netty(NIO) + 多种序列化协议 + JDK动态代理实现

依赖包解释 Guava 包含了若干被Google的 Java项目广泛依赖 的核心库&#xff0c;例如&#xff1a;集合 [collections] 、缓存 [caching] 、原生类型支持 [primitives support] 、并发库 [concurrency libraries] 、通用注解 [common annotations] 、字符串处理 [string process…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023