图神经网络基础 Graph 图以及python实现

news2024/11/27 18:42:54

摘要：
本文将介绍图的基本知识、无向图、有向图、邻接矩阵
python实现：度、连通分量、强连通图、弱连通图、图直径、度中心性、特征向量中心性、中介中心性、连接中心性等基本概念。

python计算代码：

先安装依赖：

pip install numpy pandas networks

具体代码如下所示：

import numpy as np
import pandas as pd
import networkx as nx

edges = pd.DataFrame()
edges['sources'] = [0,1,2,3,4,4,6,7,7,9,1,4,4,4,6,7,5,8,9,8]
edges['targets'] = [1,4,4,4,6,7,5,8,9,8,0,1,2,3,4,4,6,7,7,9]
#edges['weights'] = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]

G = nx.from_pandas_edgelist(edges, source='sources',target='targets')
# degree
print(nx.degree(G))
# 连通分量
print(list(nx.connected_components(G)))
# 图直径
print(nx.diameter(G))
# 度中心性
print('度中心性',nx.degree_centrality(G))
# 特征向量中心性
print('特征向量中心性',nx.eigenvector_centrality(G))
# betweenness
print('betweenness',nx.betweenness_centrality((G)))
# closeness
print('closeness',nx.closeness_centrality(G))
# pagerank
print('pagerank',nx.pagerank(G))
# HITS
print('HITS',nx.hits(G,tol=0.00001))

图

图：Graph=（V，E）
v：顶点（数据元素）的有穷非空集合；
E：边的有穷集合。
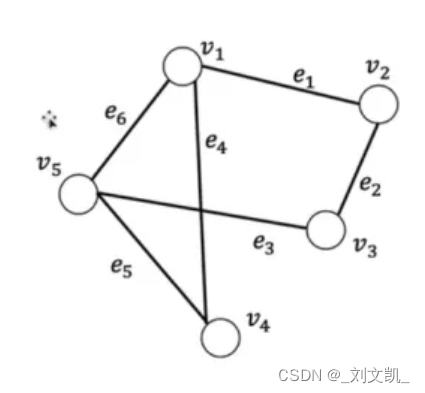
在这里插入图片描述

（1）无向图：

每条边都是无方向的，若E是无向边（简称边）的有限集合时，则图G为无向图。
边是顶点的无序对，记为（v，w）或（w，v）。
可以说w和v互为邻接点。边（v，w）依附于w和v，或称边（v，w）和v，w相关联。
在这里插入图片描述
上图可以表示为：
G1={V1，E1}，
其中V1={a，b，c，d}，
E1={（a，b），（a，c），（a，d），（b，d），（c，d）}，

（2）有向图：

若E是有向边（也称弧）的有限集合时，则图G为有向图。

有向边也叫弧，弧是顶点的有序对，记为<v，w>，其中v，w是顶点，v称为弧尾，w称为弧头，<y，w>称为从v到w的弧，也称v邻接到w.

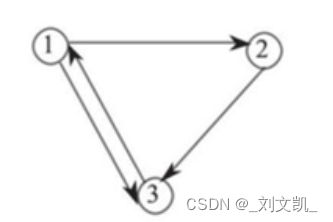
在这里插入图片描述
有向图G2，它的数据结构可以描述为：

G2=（V2，E2），
其中V2={1，2，3}，
E2={<1，2>，<1，3>，<2，3，❤️，1>}

（3）子图

设有两个图G=（V，E）和G’=（V’，E’），若V’是V的子集，且E’是E的子集，则称G’是G的子图。
若有满足v(G’）=V（G）的子图G’，则称其为G的生成子图。图中G3为G1的子图。

邻接矩阵

，我们常用邻接矩阵来表现两个节点之间的指向关系（有点类似于向量）,这个指向关系也叫做“边”。举个例子就一幕了然了：
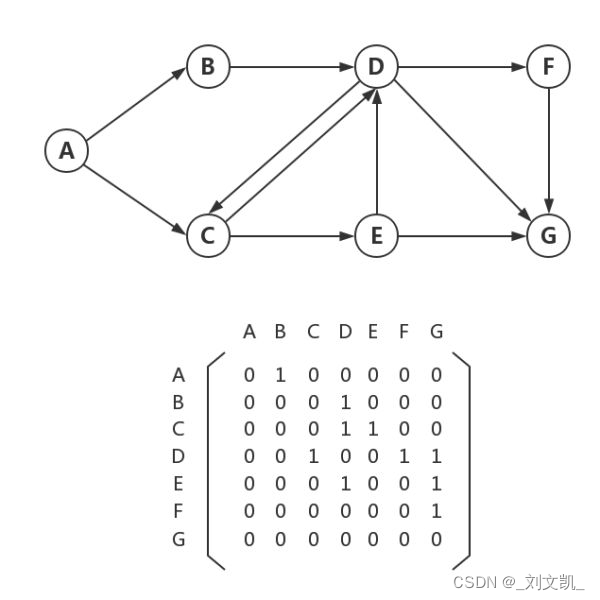
在这里插入图片描述

如下无向图所示：
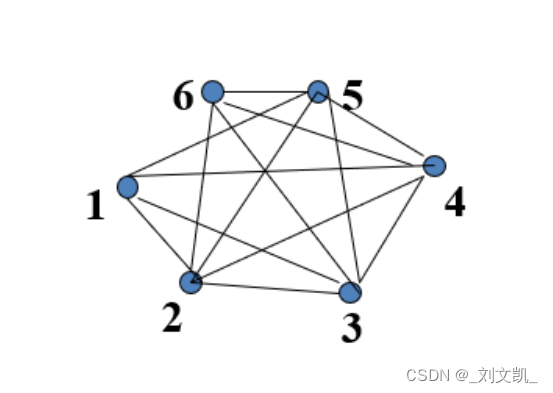
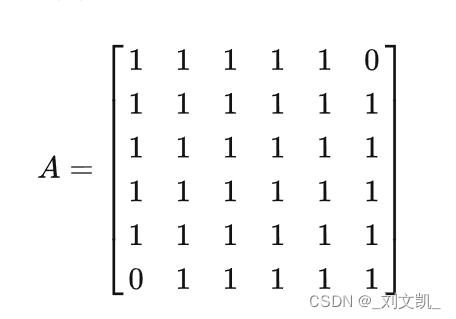
在这里插入图片描述
他的邻接矩阵可以表示为：

度

图 G=(V, E) 由下列要素构成：

一组节点（也称为 verticle）V=1,…,n
一组边 E⊆V×V
边 (i,j) ∈ E 连接了节点 i 和 j
i 和 j 被称为相邻节点（neighbor）
节点的度（degree）是指相邻节点的数量
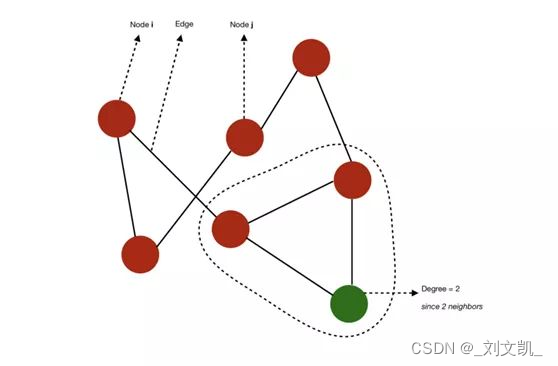
在这里插入图片描述
如果一个图的所有节点都有 n-1 个相邻节点，则该图是完备的（complete）。也就是说所有节点都具备所有可能的连接方式。从 i 到 j 的路径（path）是指从 i 到达 j 的边的序列。该路径的长度（length）等于所经过的边的数量。
图的直径（diameter）是指连接任意两个节点的所有最短路径中最长路径的长度。举个例子，在这个案例中，我们可以计算出一些连接任意两个节点的最短路径。该图的直径为 3，因为没有任意两个节点之间的最短路径的长度超过 3。

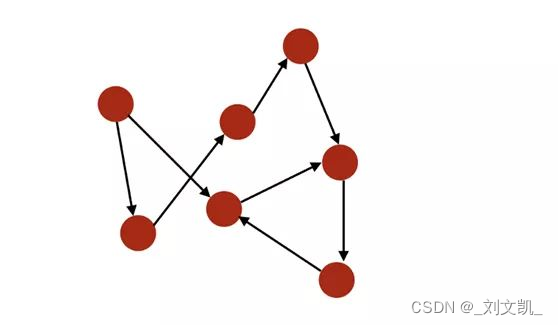
如果一个图的边是有顺序的配对，则该图是有向的（directed）。i 的入度（in-degree）是指向 i 的边的数量，出度（out-degree）是远离 i 的边的数量。
在这里插入图片描述

度中心性 Degree Centrality

在网络中，一个节点的度越大，就意味着这个节点的度中心性就越高，就说明在网络中这个节点越重要。
在这里插入图片描述

其中，n表示节点的数量，N-degree 表示该节点的度。

特征向量中心性 Eigenvector Centrality

一个节点的重要性取决于其邻居节点的数量（即该节点的度），也取决与其邻居节点的重要性。与之相连的邻居节点越重要，则该节点就越重要。
计算过程为：由邻接矩阵求邻接矩阵的特征值，由此求特征向量，选择最大特征值对应的特征向量作为EC

特征向量中心性的计算公式如下：
在这里插入图片描述

中介中心性 Between Centrality

以经过某个节点的最短路径数目来刻画节点的重要性指标。
其中dst表示s到t的最短路径数量，dst()表示从s到t的最短路径中经过节点的数量。若需要进行标准化，在如上公式基础上，除以（n-1)(n-2)，n为节点数量。在这里插入图片描述

紧密中心性 Closeness Centrality (连接中心性）

反映在网络中某一节点与其他节点之间的接近程度。如果一个节点离其他的节点都很近，那么传递信息的时候就不需要依赖其他的节点，说明这个节点很重要。
在这里插入图片描述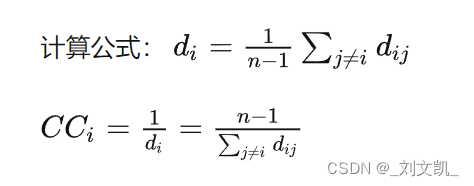
这个点的紧密中心性是基于该节点到网络中其余所有节点的最短路径之和，如果进行归一化处理，就是求这个节点到其他所有节点的平均最短距离。一个节点的平均最短距离越小，那么这个进行的紧密中心性就越大。如果节点i和节点j之间没有路径可达，则定义dij为无穷大，其倒数为0.