1. 数据准备
1.1 计算因子IC重要函数
def get_clean_factor_and_forward_returns(factor,
prices,
groupby=None,
binning_by_group=False,
quantiles=5,
bins=None,
periods=(1, 5, 10),
filter_zscore=20,
groupby_labels=None,
max_loss=0.35,
zero_aware=False,
cumulative_returns=True)
- factor: pd.Series - MultiIndex 因子数据
- prices:pd.DataFrame 价格数据,注意避免使用未来函数,例如可以使用第二天的开盘价
- groupby : pd.Series - MultiIndex or dict 分组,如行业分组
- binning_by_group : bool 是否分组进行计算
- quantiles : int or sequence[float] 将股票按数量等分
- bins : int or sequence[float] 按因子值等宽进行划分
- periods : sequence[int] 收益计算周期/调仓周期
- filter_zscore : int or float, optional 异常阈值的倍数,用来过滤掉涨跌幅特别大的股票,会导致前视偏差
- groupby_labels : dict 分组标签
- max_loss : float, optional 允许丢弃的最多的的数据的比例
- zero_aware : bool, optional是否正负信号分开算
- cumulative_returns : bool, optional 是否计算单利
- 返回值 merged_data : pd.DataFrame - MultiIndex
1.2 准备因子数据
- factor: pd.Series - MultiIndex 因子数据

- 聚宽数据,本地运行计算
code = ["IC9999.CCFX", "IH9999.CCFX", "IF9999.CCFX"]
start_date = "2022-1-18"
end_date = "2023-1-18"
fre = "1d"
period = 5
# Todo: 循环获取因子数据
factor_df = pd.DataFrame()
for future in code:
df = get_price(future, start_date=start_date, end_date=end_date, frequency=fre, panel=False)
df["mom"] = momentum_factor(df, time_period=period)
df["code"] = [future] * len(df)
factor_df = pd.concat([factor_df, df[["code", "mom"]]])
factor_df = factor_df.reset_index()
factor_df = factor_df.sort_values(by="index")
factor_df = factor_df.set_index(["index", "code"])
print(factor_df)
- 运行结果
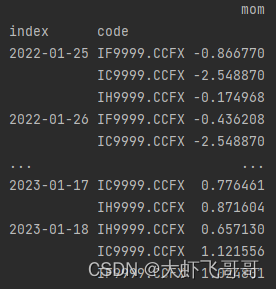
- 取单个因子,将 将MutlIndex DataFrame —> MutlIndex Series
factor_series = factor_df["mom"]
print(factor_series)
- 运行结果
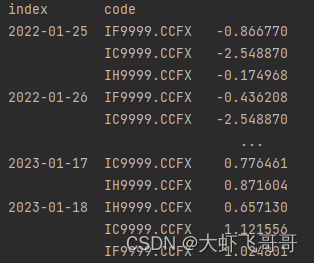
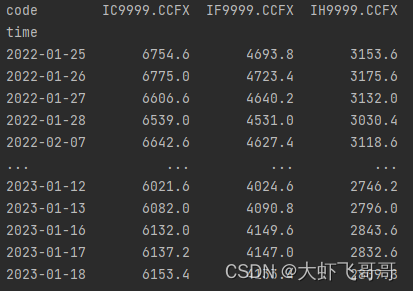
1.3 行情数据准备
- prices:pd.DataFrame 价格数据
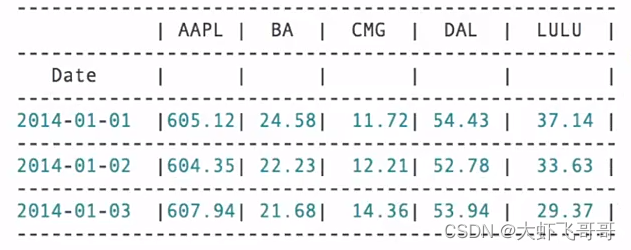
- 聚宽数据,本地运行计算
code = ["IC9999.CCFX", "IH9999.CCFX", "IF9999.CCFX"]
df = get_price(code, start_date=start_date, end_date=end_date, frequency=fre, panel=False, fields=["close"])
df = df.set_index(["time", "code"])
df = df.close.unstack()
- 运行结果
1.4 注意点
需要修改 alphalens.utils.compute_forward_returns中源码(342行)
# df.index.levels[0].name = "date"
# df.index.levels[1].name = "asset"
df.index.set_names(["date", "asset"], inplace=True)
2. 计算
2.1 IC 计算以及结果展示
# Todo: 生成alphalens通用结构
factor_return = utils.get_clean_factor_and_forward_returns(factor_series, df)
print(factor_return)
# 获取每天的IC结果
res_ic = performance.factor_information_coefficient(factor_return)
print(res_ic)
alphalens.plotting.plot_ic_ts(res_ic)
alphalens.plotting.plot_ic_hist(res_ic)
alphalens.plotting.plot_ic_qq(res_ic)
plt.show()
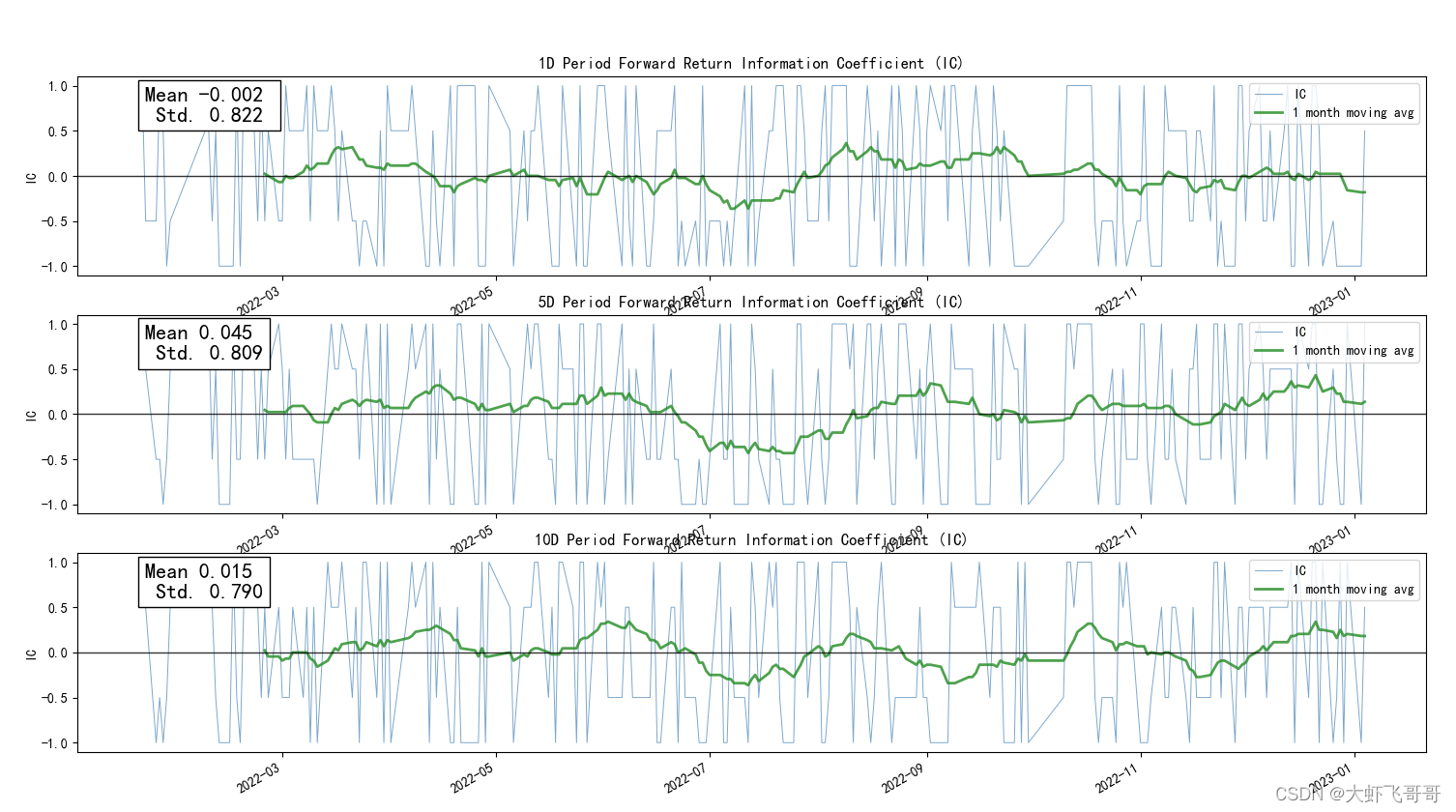
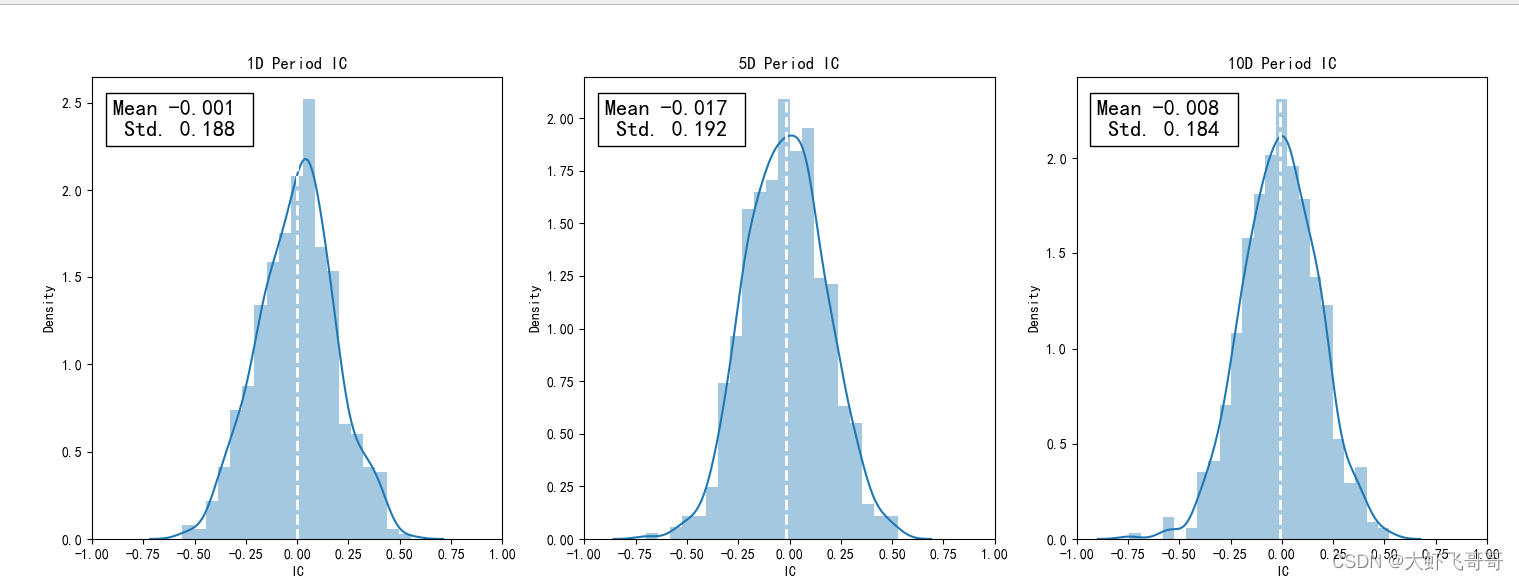
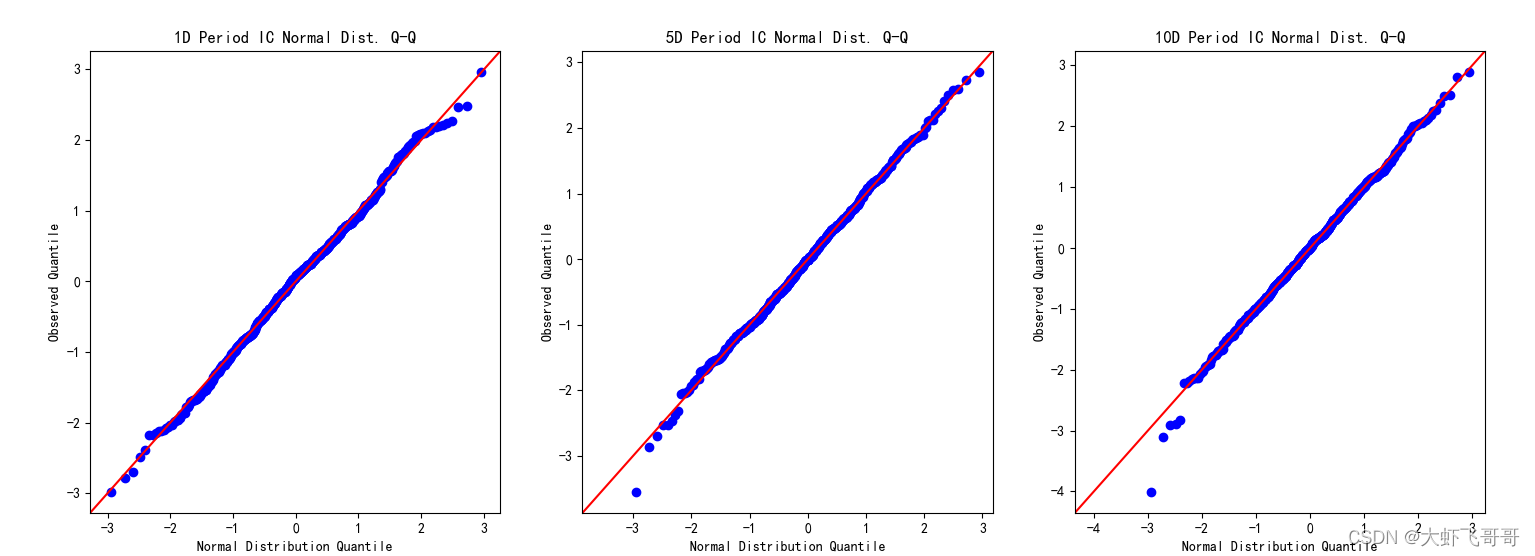
2.2 因子收益率
- 因子收益率是在固定周期内对因子暴露值和下期的收益率之间建立横截面回归方程。
- 得到的权重系数即为因子收益率。
- 因子的收益率与股票的收益率是有区别
- 股票收益率:收盘之间计算
- 因子的收益率:横截面数据回归方程得来, 特征值就是因子值,目标值是股票收益率

factor_pnl = tears.create_returns_tear_sheet(factor_return)
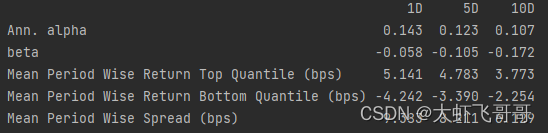
- 返回表格内容
- 给每个股票在每一天都打了分,那么,你得按照这个分数来分层次
- 分5个层次,那么得分前20%的是第一层,即Top Quantile,最后面20%的是Bottom Quantile
- 1、5、10,也就是按照每天调仓、一周调仓、半
- 个月调仓来进行因子的测试
- 第一行是按照这样的调仓周期,获得的年化alpha,beta(这里,alphalens中的beta是全市场的平均收益,而这里的全市场是每一个层加起来的平均收益)
- 后面是每个层的收益。
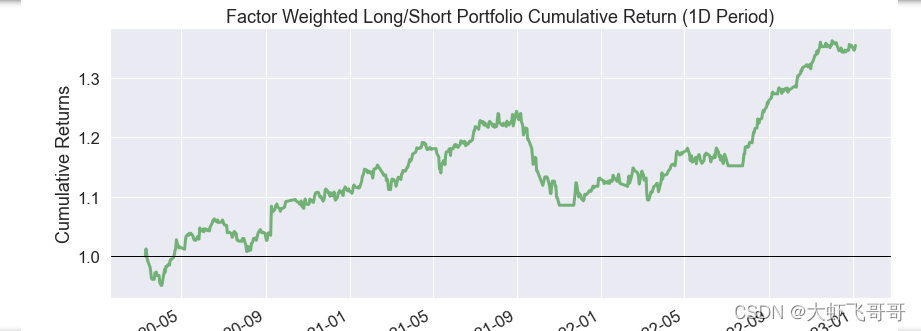
- 因子的方向:从小到大、从大到小、中间的位置
- 用于回测的时候选股位置使用
- 对第五组有正向预测,对第一组是方向预测

- 分组因子的累积收益(一期)
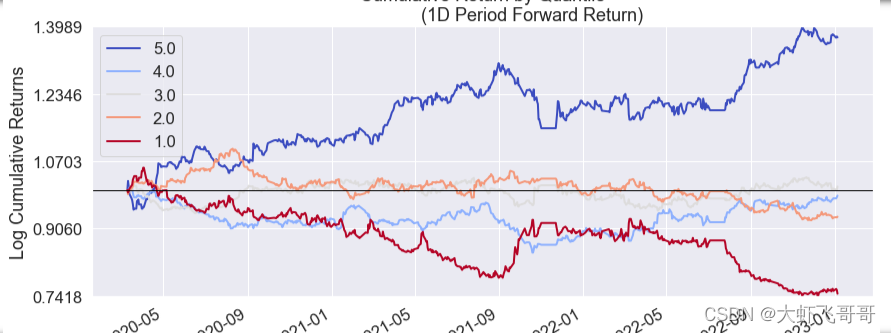
- 收益移动平均线
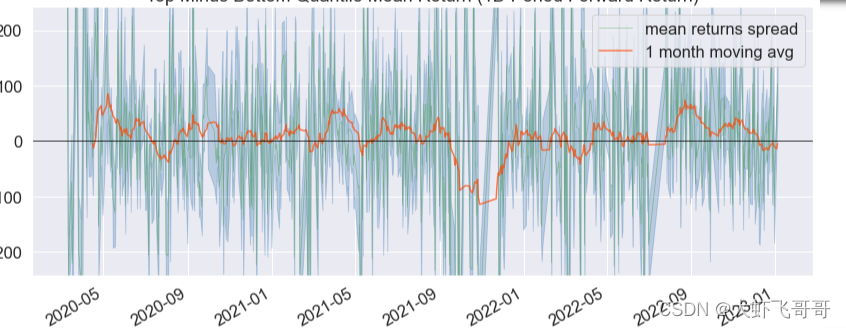
2.3 统计指标
| 因子名称 | 因子平均收益 | IC mean | IC std | IC > 0.02 | IR |
|---|---|---|---|---|---|
| 0.0004 | -0.017 | 0.192 | 0.425 | -0.0885 |
|
- 第三列数据:在筛选因子的时候,会考虑某段时间的平均值大小。判断平均值大于某个数字,IC的值一般根据筛选严格程度取值,这个值可以自定义0.06意味筛选严格,大于 0.02会放松筛选(可以用在对开始很多因子的海选中) IC 大于 0.02 的比例
- IR = IC mean / IC std IR值越大越稳定
- 期货分层回测计算因收益

2.3 打分依据
- 因子平均收益 > 0.002
- IC mean > 0.03
- IC > 0.02(50%)
- IR > 0.3
2.4 研报统计结果
2.5 注意点
-
用到19号的期货数据计算得到的因子值,是20号的因子值
-
用到19号的期货数据计算得到的因子值,不能用于19号价格的预测,存在未来函数
-
传递给Alphalens的价格数据需要包含资产的进入价格,也就是在某个时间点观察到因子取值后,下一个可买入的价格。这个价格一定不能用于此次因子的计算。这一点一定要反复检查,以免在研究中引入前视偏差。
-
可以使用19号close价格计算因子,20号的open价格计算IC值
-
当因子IC超过0.1时,要注意检查
-
用到19号的期货数据计算得到的因子值,是20号的因子值
-
用到19号的期货数据计算得到的因子值,不能用于19号价格的预测,存在未来函数
-
传递给Alphalens的价格数据需要包含资产的进入价格,也就是在某个时间点观察到因子取值后,下一个可买入的价格。这个价格一定不能用于此次因子的计算。这一点一定要反复检查,以免在研究中引入前视偏差。
-
可以使用19号close价格计算因子,20号的open价格计算IC值
-
当因子IC超过0.1时,要注意检查