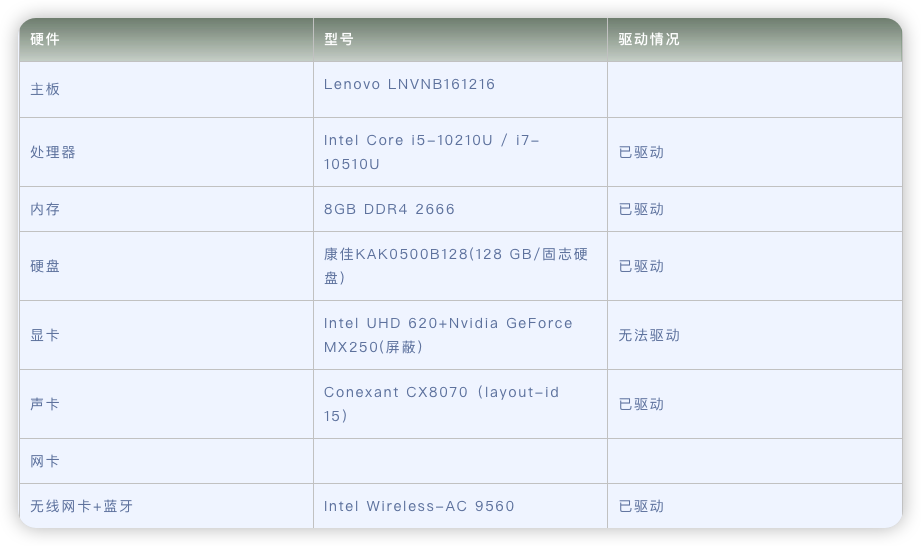
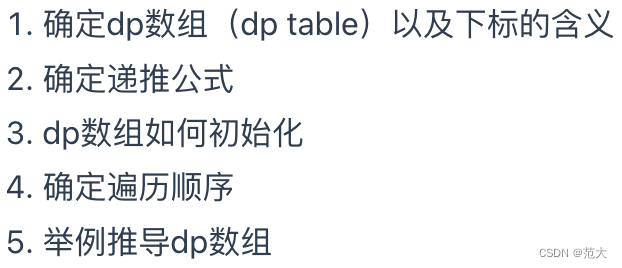
基本步骤

509. 斐波那契数

递归版本

class Solution {
    public int fib(int n) {
        if(n==0){
            return 0;
        }
        if(n==1){
            return 1;
        }
        return fib(n-1)+fib(n-2);
    }
}

动态规划版本

class Solution {
    public int fib(int n) {
        int[] dp = new int[n+1];
        if(n<=1){
            return n;
        }
        
        dp[0]=0;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}

优化后，不用存储一整个数组，只需要存储三个数即可

class Solution {
    public int fib(int n) {
        int[] dp = new int[2];
        if(n<=1){
            return n;
        }
        dp[0]=0;
        dp[1]=1;

        int sum=0;
        for(int i=2;i<=n;i++){
            sum = dp[0]+dp[1];
            dp[0]=dp[1];
            dp[1]=sum;

        }
        return sum;
    }
}

这也是动态规划的常见优化方式，优化额外的存储空间。

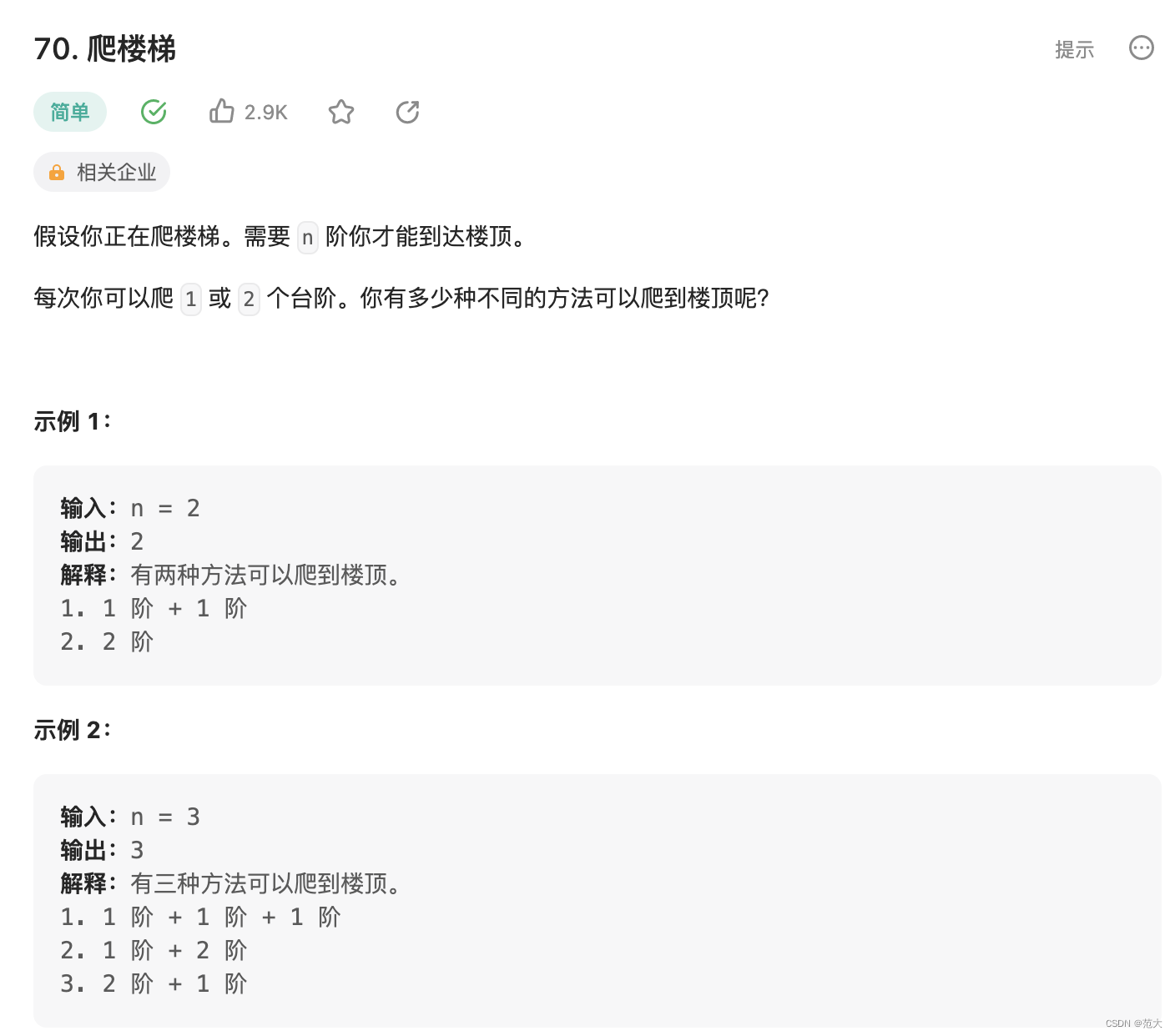
70. 爬楼梯

class Solution {
    public int climbStairs(int n) {
        int[] dp = new int[n+1];
        if(n<=1){
            return 1;
        }
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];

    }
}

其实就是斐波那契数列，可自行优化

746. 使用最小花费爬楼梯

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        // dp[i]到达第i个台阶需要支付的最低花费，注意到达该台阶本身并不需花费,即不管cost[i]，只有往上跳了才会产生花费
        int[] dp = new int[cost.length+1];
        if(cost.length==2){
            return Math.min(cost[0],cost[1]);
        }
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<=cost.length;i++){
            dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.length];
    }
}

稀里糊涂也写了另一个版本，到达每个台阶的最低花费中，把自身跳的花费也计算了进去，最后到达楼顶的花费，即是倒数第一阶和倒数第二阶的花费最小值。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length];
        if(cost.length==2){
            return Math.min(cost[0],cost[1]);
        }
        dp[0]=cost[0];
        dp[1]=cost[1];
        for(int i=2;i<cost.length;i++){
            dp[i]=Math.min(dp[i-1],dp[i-2])+cost[i];
        }
        return Math.min(dp[cost.length-1],dp[cost.length-2]);
    }
}

建议直接看前一个版本，更好理解。

62.不同路径

class Solution {
    public int uniquePaths(int m, int n) {
    // dp[i][j]表示从(0,0)到(i,j)有多少条不同路径
        int[][] dp = new int[m][n];
        for(int i=0;i<m;i++){
            dp[i][0]=1;
        }
        for(int i=0;i<n;i++){
            dp[0][i]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

优化成两行数组

class Solution {
    public int uniquePaths(int m, int n) {
        if(m==1 || n==1){
            return 1;
        }
        int[][] dp = new int[2][n];
        dp[1][0]=1;
        for(int i=0;i<n;i++){
            dp[0][i]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[1][j] = dp[0][j] + dp[1][j-1];
                dp[0][j]=dp[1][j];
                dp[0][j-1] = dp[1][j-1];
            }
        }
        return dp[1][n-1];
    }
}

进一步优化成一行数组

class Solution {
    public int uniquePaths(int m, int n) {
        if(m==1 || n==1){
            return 1;
        }
        int[] dp = new int[n];
        for(int i=0;i<n;i++){
            dp[i]=1;
        }
       
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
               dp[j] = dp[j] + dp[j-1];
            }
        }
        return dp[n-1];
    }
}

dp[j] = dp[j] + dp[j-1];
当你遍历到第j个元素时，当前里面存着的其实是上一次遍历存储的j,即上一行的(i-1,j)，由于是从左到右遍历的，而j-1的元素刚刚更新完，即(i,j-1)，所以直接dp[j] = dp[j] + dp[j-1]即可

63. 不同路径 II

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];

        // 初始化，若第一行或第一列有障碍物，则后面的路径数皆为0
        for(int i=0;i<m&&obstacleGrid[i][0]==0;i++){
            dp[i][0]=1;
        }
        for(int i=0;i<n&&obstacleGrid[0][i]==0;i++){
            dp[0][i]=1;
        }

        // 从第二行或第二列开始遍历
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j] == 0){
                   dp[i][j]=dp[i-1][j] + dp[i][j-1];
                }
 
            }
        }

        return dp[m-1][n-1];


    }
}

直接优化成一维数组

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[] dp = new int[n];

        // 如果终点有障碍物，直接返回0
        if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1){
            return 0;
        }

        // 初始化，有障碍物，则后面的路径数皆为0
        for(int i=0;i<n&&obstacleGrid[0][i]==0;i++){
            dp[i]=1;
        }

        // dp[0]只需要处理一次，如果第一行第一列无障碍物，则dp[0]为1
        // 后续遍历时，如果其他行第一列有障碍物，则dp[0]=0，而之后的遍历中，dp[0]一直都是0
        // 如果后续第一列无障碍物，则dp[0]=1也一直不会改变
       
        for(int i=1;i<m;i++){
            for(int j=0;j<n;j++){
                if(obstacleGrid[i][j] == 1){
                    // 如果其他行第一列有障碍物，则dp[0]=0
                   dp[j]=0;
                }else if(j>0){
                     dp[j]=dp[j-1] + dp[j];
                }
            }
        }
        return dp[n-1];
    }
}

这里对dp[0]的处理有些巧妙。

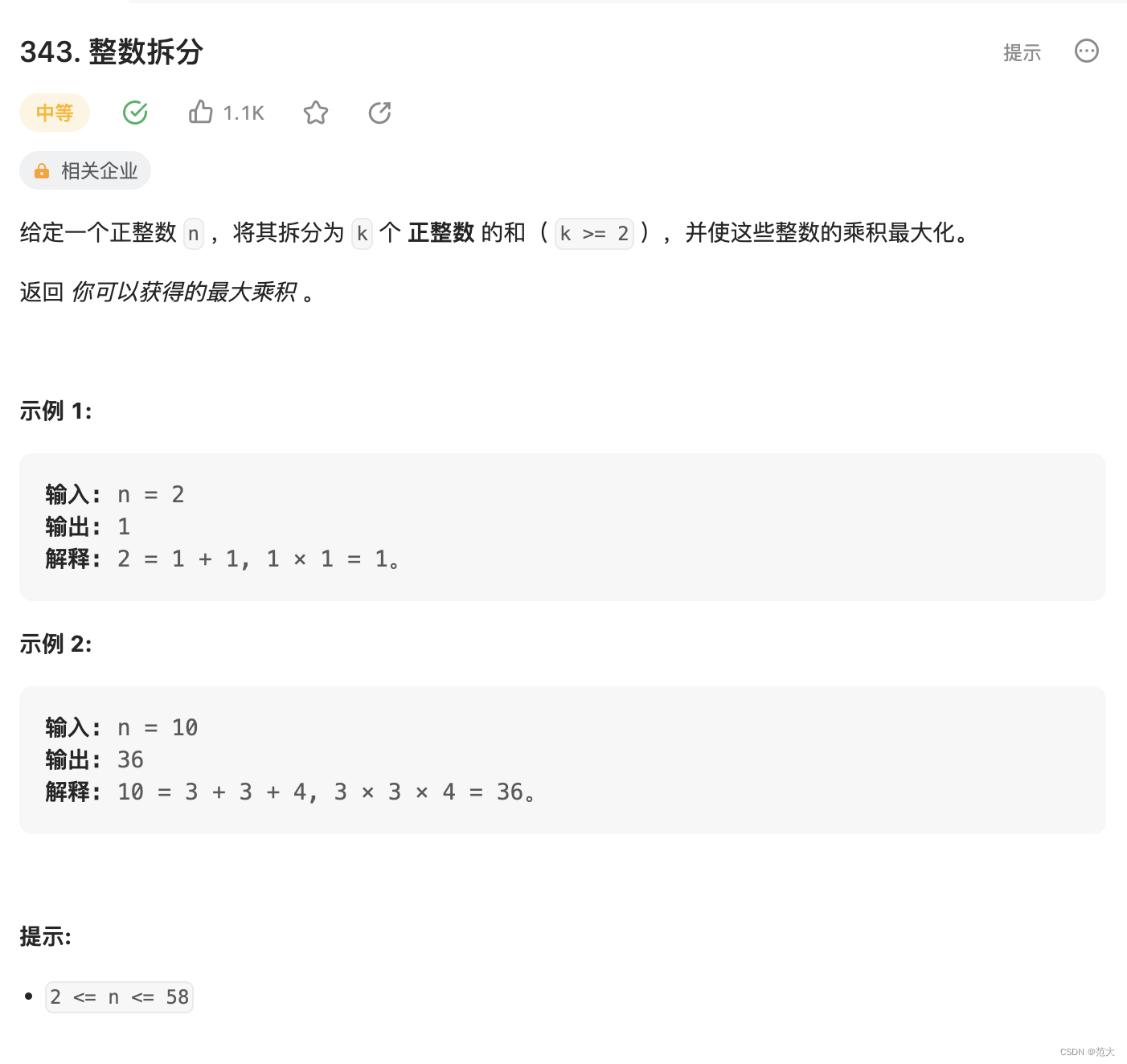
343. 整数拆分

class Solution {
    public int integerBreak(int n) {
        // dp[i]是正整数i可拆分出的最大乘积
        // dp[i] = max{dp[j]*dp[i-j]} j>0且j<i
        // dp[2]=1 dp[3]=2
        int[] dp = new int[n+1];
        dp[2]=1;
        for(int i=3;i<=n;i++){
            int sum=0;
            // 后半部分就开始重复了 1x4 2x3 3x2 4x1
            for(int j=1;j<=i/2;j++){                
                sum = Math.max(sum,Math.max(j,dp[j])*Math.max(dp[i-j],i-j));
            }
            dp[i] = sum;
        }
        return dp[n];
    }
}

其中的Math.max(j,dp[j]) 其实直接用j即可，但是我无法理解，所以就没改

96.不同的二叉搜索树

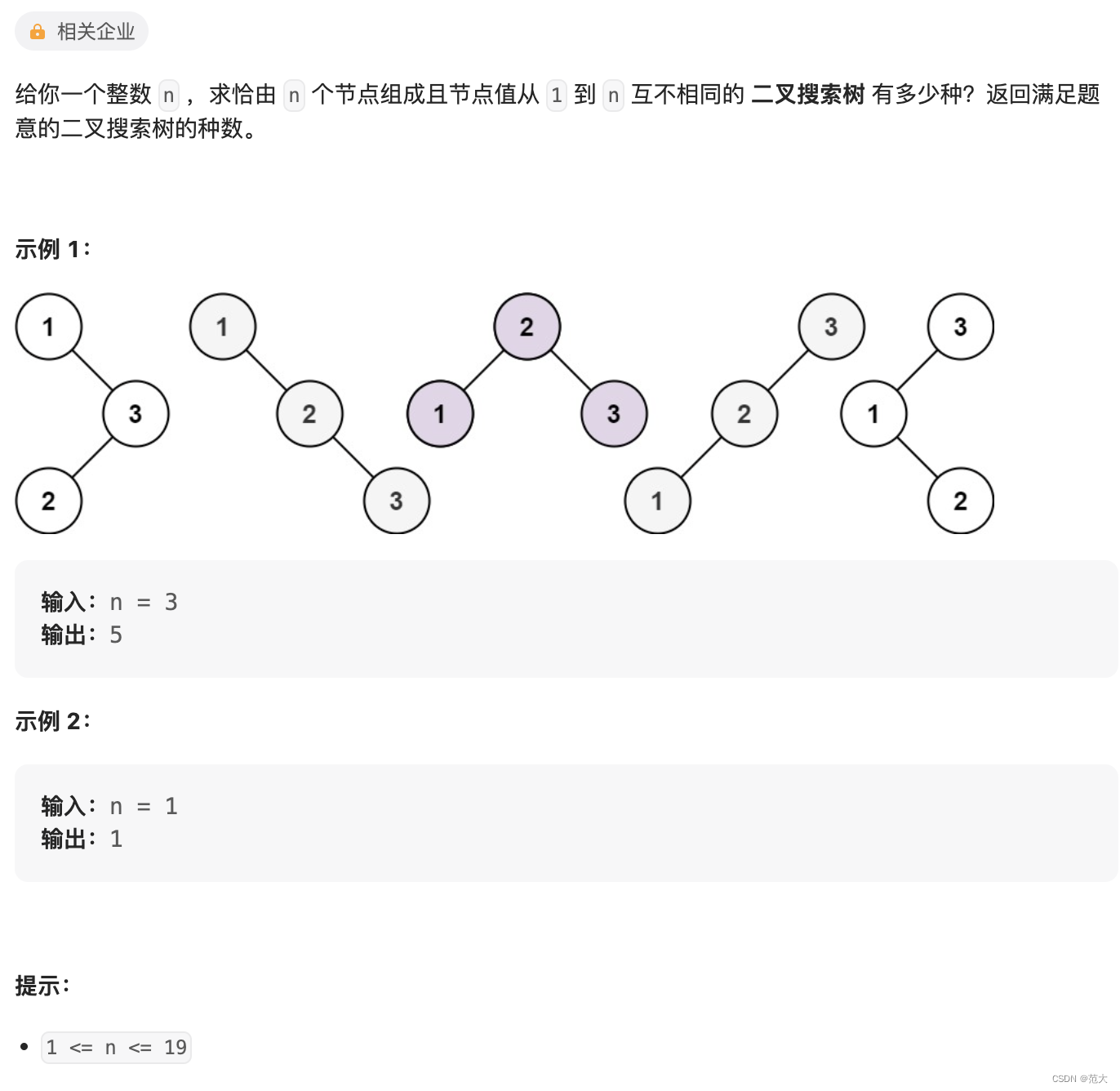
class Solution {
    public int numTrees(int n) {
        // gn = g0 * gn-1 + g1 * gn-2
        int[] dp = new int[n+1];
        if(n<=2){
            return n;
        }
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i] += dp[j-1]*dp[i-j];
            }
        }

        return dp[n];
    }
}