目录

一、拓扑排序的思想

二、代码实现（C++）

代码思想

核心代码

完整代码

---

一、拓扑排序的思想

        以西红柿炒鸡蛋这道菜为例，其中的做饭流程为：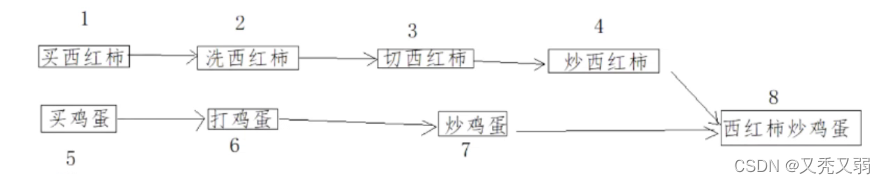

        中间2 6 3 7 4的顺序都可以任意调换，但1和5必须在最前面，这是饭前准备，8必须在最后面。1和5的入度为0，出度为1，8的入度都2，出度为0 

        在这个操作流程内，把每个步骤当作一个顶点，排序连接起来就是个有向图。

        排序，都是将元素按照一定的顺序/规则排列

        拓扑排序就是将元素按照先后顺序进行排序

        书面解释是：在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为 AOV网(Activity On VertexNetwork)。AOV 网中的弧表示活动之间存在的某种制约关系。

        特点是：有向无环(无回路)

        拓扑序列：设G=(V,E)是一个具有 n个顶点的有向图V中的顶点序列 V1，V2····满足若从顶点到有一条路径，则在顶点序列中顶点必在顶点之前。则我们称这样的顶点序列为一个拓扑序列。

        拓扑排序就是对一个有向图构造拓扑序列的过程。构造时会有两个结果，如果此网的全部顶点都被输出，则说明它是不存在环(回路)的AOV 网，如果输出顶点数少了，哪怕是少了一个，也说明这个网存在环(回路)，不是AOV 网

       拓扑排序的价值在于，不存在回路的AOV 网，我们可以将它应用在各种各样的工程或项目的流程图中，满足各种应用场景的需要。

二、代码实现（C++）

代码思想

        从入度为0的顶点开始访问，访问完成后，将以此顶点为狐尾的弧删除(此顶点的邻接表中的顶点入度都减少1)，然后继续查找剩余顶点中入度为0的顶点，重复操作，直到所有顶点都被访问完，或者没有了入度为0的顶点(说明此AOV有回路)

        标记V1是从哪个顶点来的，借助栈来存储入度为0的顶点，栈的思想是先入后出

        需要借助邻接表来存储图，邻接表内添加一个属性：顶点的入度，当创建图时，路径中每添加一条边时，就将入度+1，如果是v0->b1,则v1的度+1

        先遍历度为0的节点，将其入栈，对栈顶元素在邻接表内查找其下一个顶点，并将下个顶点的度-1，设置为0。直到以该顶点所在的邻接表内的顶点的度都设置为0时，即代表将该顶点的狐尾删除。

        以该图为例，一张电影制作图，实现其中节点之间关联的排序

 

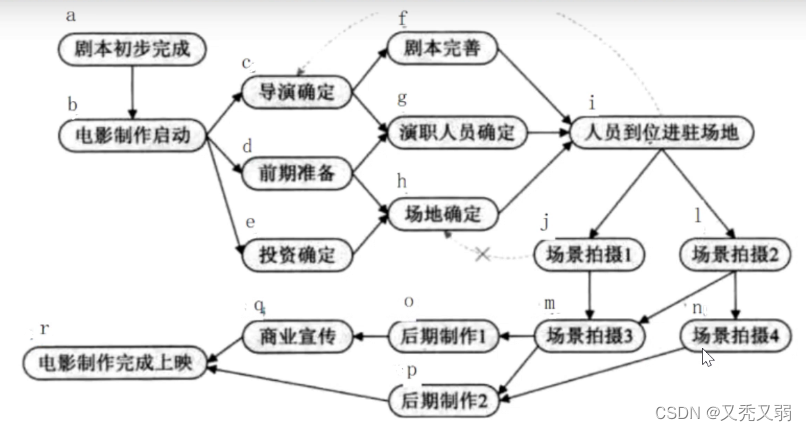
核心代码

int Graph::GetVertexIndex(char v)//获取顶点所在的下标
{
	int i;
	for (i = 0; i < m_NumVertex; i++)
	{
		if (m_VerArr[i].m_value == v)
			return i;
	}
	return -1;
}
void Graph::InsertVertex(char v)//插入顶点
{
	if (m_NumVertex >= m_MaxVertex)
		return;
	m_VerArr[m_NumVertex++].m_value = v;
}

void Graph::InsertEdge(char v1, char v2) //插入边
{
	int p1index = GetVertexIndex(v1);
	int p2index = GetVertexIndex(v2);
	if (p1index == -1 || p2index == -1)
		return;
	//v1-v2
	Edge* p = new Edge(p2index);
	p->m_next = m_VerArr[p1index].m_list;
	m_VerArr[p1index].m_list = p;
	m_VerArr[p2index].m_verIn++;
}
void Graph::TopologicalSort()//拓扑排序
{
	stack<int> ss;
	int i;
	Edge* p = NULL;
	for (i = 0; i < m_NumVertex; i++) //将入度为0的顶点入栈
	{
		if (m_VerArr[i].m_verIn == 0)
			ss.push(i);
	}
	for (i = 0; i < m_NumVertex; i++)//循环访问所有顶点进行拓扑排序
//该循环结束的条件：1.循环完，没有度为0的顶点再入栈即栈为空时，退出循环
	{
		if (ss.empty())
		{
			cout << "有回路" << endl;
			return;
		}
		else
		{
			int top = ss.top();//获取栈顶元素并出栈
			ss.pop();
			cout << m_VerArr[top].m_value << " ";//输出
			p = m_VerArr[top].m_list;//让P指向刚出来顶点的邻接表
			while (p)//循环遍历邻接表，设置入度-1
			{
				int in = --m_VerArr[p->m_destindex].m_verIn;//in为p所指向顶点的入度-1
				if (in == 0)
				{
					ss.push(p->m_destindex);//入度为0时，说明顶点就是入读为0的顶点，对其下标入栈
				}
				p = p->m_next;
			}
		}
	}
	cout << endl;
}

完整代码

#include<iostream>
using namespace std;
#define SIZE 20
class Edge //边
{
public:
	Edge() :m_next(NULL) {}
	Edge(int index) :m_destindex(index), m_next(NULL) {}
	int m_destindex;
	Edge* m_next;
};
class Vertex //顶点
{
public:
	Vertex() :m_list(NULL),m_verIn(0) {}
	Vertex(char v) :m_value(v), m_list(NULL),m_verIn(0) {}
	char m_value;
	Edge* m_list;
	int m_verIn;
};
class Graph
{
public:
	Graph();
	~Graph();
	void InsertVertex(char v);
	void InsertEdge(char v1, char v2);
	int GetVertexIndex(char v);
	void ShowGraph();
	void TopologicalSort();
private:
	int m_MaxVertex;
	int m_NumVertex;
	//Vertex* m_VerArr;
	Vertex m_VerArr[SIZE];
};

#include<stack>
void Graph::TopologicalSort()//拓扑排序
{
	stack<int> ss;
	int i;
	Edge* p = NULL;
	for (i = 0; i < m_NumVertex; i++)
	{
		if (m_VerArr[i].m_verIn == 0)
			ss.push(i);
	}
	for (i = 0; i < m_NumVertex; i++)
	{
		if (ss.empty())
		{
			cout << "有回路" << endl;
			return;
		}
		else
		{
			int top = ss.top();
			ss.pop();
			cout << m_VerArr[top].m_value << " ";
			p = m_VerArr[top].m_list;
			while (p)
			{
				int in = --m_VerArr[p->m_destindex].m_verIn;
				if (in == 0)
				{
					ss.push(p->m_destindex);
				}
				p = p->m_next;
			}
		}
	}
	cout << endl;
}
void Graph::ShowGraph()
{
	Edge* p = NULL;
	for (int i = 0; i < m_NumVertex; i++)
	{
		cout << i << " " <<m_VerArr[i].m_verIn<<" "<< m_VerArr[i].m_value << "->";
		p = m_VerArr[i].m_list;
		while (p != NULL)
		{
			cout << p->m_destindex << "->";
			p = p->m_next;
		}
		cout << "nul" << endl;
	}
}
int Graph::GetVertexIndex(char v)
{
	int i;
	for (i = 0; i < m_NumVertex; i++)
	{
		if (m_VerArr[i].m_value == v)
			return i;
	}
	return -1;
}
void Graph::InsertVertex(char v)
{
	if (m_NumVertex >= m_MaxVertex)
		return;
	m_VerArr[m_NumVertex++].m_value = v;
}
Graph::Graph()
{
	m_MaxVertex = SIZE;
	m_NumVertex = 0;
	//m_VerArr = new Vertex[m_MaxVertex];
}
Graph::~Graph()
{
	/*	if (m_VerArr != NULL)
		{
			delete[]m_VerArr;
			m_VerArr = NULL;
		}*/
	m_NumVertex = 0;
}
void Graph::InsertEdge(char v1, char v2)
{
	int p1index = GetVertexIndex(v1);
	int p2index = GetVertexIndex(v2);
	if (p1index == -1 || p2index == -1)
		return;
	//v1-v2
	Edge* p = new Edge(p2index);
	p->m_next = m_VerArr[p1index].m_list;
	m_VerArr[p1index].m_list = p;
	m_VerArr[p2index].m_verIn++;
}
void main()
{
	Graph g;//构建一个图
	g.InsertVertex('a');
	g.InsertVertex('b');
	g.InsertVertex('c');
	g.InsertVertex('d');
	g.InsertVertex('e');
	g.InsertVertex('f');
	g.InsertVertex('g');
	g.InsertVertex('h');
	g.InsertVertex('i');
	g.InsertVertex('j');
	g.InsertVertex('l');
	g.InsertVertex('m');
	g.InsertVertex('n');
	g.InsertVertex('o');
	g.InsertVertex('p');
	g.InsertVertex('q');
	g.InsertVertex('r');
	g.InsertEdge('a', 'b');
	g.InsertEdge('b', 'c');
	g.InsertEdge('b', 'd');
	g.InsertEdge('b', 'e');
	g.InsertEdge('c', 'f');
	g.InsertEdge('c', 'g');
	g.InsertEdge('d', 'g');
	g.InsertEdge('d', 'h');
	g.InsertEdge('e', 'h');
	g.InsertEdge('f', 'i');
	g.InsertEdge('g', 'i');
	g.InsertEdge('h', 'i');
	g.InsertEdge('i', 'j');
	g.InsertEdge('i', 'l');
	g.InsertEdge('j', 'm');
	g.InsertEdge('l', 'n');
	g.InsertEdge('l', 'm');
	g.InsertEdge('m', 'o');
	g.InsertEdge('m', 'p');
	g.InsertEdge('n', 'p');
	g.InsertEdge('o', 'q');
	g.InsertEdge('p', 'r');
	g.InsertEdge('q', 'r');
	g.ShowGraph();
	g.TopologicalSort();
}

对各顶点和边的添加：第一列是顶点，第二列是计算所有顶点的入度情况，第三列是邻接表