-
BatchNorm 最早在全连接网络中被提出,对每个神经元的输入做归一化。扩展到 CNN 中,就是对每个卷积核的输入做归一化,或者说在 channel 之外的所有维度做归一化。 BN 带来的好处有很多,这里简单列举几个:
-
防止过拟合:单个样本的输出依赖于整个 mini-batch,防止对某个样本过拟合。
-
加快收敛:梯度下降过程中,每一层的权重矩阵W和偏置b都会不断变化,导致输出结果的分布在不断变化,后层网络就要不停地去适应这种分布变化。用 BN 后,可以使每一层输入的分布近似不变。
-
防止梯度弥散:forward 过程中,逐渐往非线性函数的取值区间的上下限两端靠近,(以 Sigmoid 为例),此时后面层的梯度变得非常小,不利于训练。
-
-
BN 的数学表达为:
-
y = x − E ( x ) D ( x ) + η ∗ γ + β y=\frac{x-E(x)}{\sqrt{D(x)+\eta}}*\gamma+\beta y=D(x)+ηx−E(x)∗γ+β
-
这里引入了缩放因子 γ \gamma γ和平移因子 β \beta β,作者在文章里解释了它们的作用:
-
Normalize 到 均值为0,方差为1, 会导致新的分布丧失从前层传递过来的特征与知识。
-
以 Sigmoid 为例,加入 γ \gamma γ, β \beta β , 可以防止大部分值落在近似线性的中间部分,导致无法利用非线性的部分。
-
-
BatchNorm 默认打开
track_running_stats,因此每次 forward 时都会依据当前 minibatch 的统计量来更新running_mean和running_var。-
r u n n i n g _ m e a n = r u n n i n g _ m e a n ∗ ( 1 − m o m e n t u n ) + E ( x ) ∗ m o m e n t u n r u n n i n g _ v a r = r u n n i n g _ v a r ∗ ( 1 − m o m e n t u n ) + V a r ( x ) ∗ m o m e n t u n running\_mean=running\_mean*(1-momentun)+E(x)*momentun\\ running\_var=running\_var*(1-momentun)+Var(x)*momentun running_mean=running_mean∗(1−momentun)+E(x)∗momentunrunning_var=running_var∗(1−momentun)+Var(x)∗momentun
-
momentum默认值为 0.1,控制历史统计量与当前 minibatch 在更新running_mean、running_var时的相对影响。
-
-
其中E(x),Var(x) 、 分别表示x的均值、方差;需要注意这里统计方差用了无偏估计。
-
running_var = running_var * (1 - momentum) + momentum * inputs_var * n / (n - 1) running_mean = running_mean * (1 - momentum) + momentum * inputs_mean
-
-
-
γ , β \gamma,\beta γ,β的更新
- BatchNorm 的
weight,bias分别对应公式里的 γ \gamma γ, β \beta β , 更新方式是梯度下降法。
- BatchNorm 的
-
在train和eval不同模式上,batchNorm会有不同:
- train 模式下统计
running_mean和running_var,eval 模式下用统计数据作为 μ \mu μ 和 δ \delta δ 。track_running_stats默认为True,极为训练模式,设置为False时,eval模式直接计算输入的均值和方差。
- train 模式下统计
-
SyncBatchNorm
-
BN 的性能和 batch size 有很大的关系。batch size 越大,BN 的统计量也会越准。然而像检测这样的任务,占用显存较高,一张显卡往往只能拿较少的图片(比如 2 张)来训练,这就导致 BN 的表现变差。一个解决方式是 SyncBN:所有卡共享同一个 BN,得到全局的统计量。
-
单卡上的 BN 会计算该卡对应输入的均值、方差,然后做 Normalize;SyncBN 则需要得到全局的统计量,也就是“所有卡上的输入”对应的均值、方差。一个简单的想法是分两个步骤:
-
每张卡单独计算其均值,然后做一次同步,得到全局均值
-
用全局均值去算每张卡对应的方差,然后做一次同步,得到全局方差
-
-
但两次同步会消耗更多时间,事实上一次同步就可以实现 μ \mu μ 和 δ 2 \delta^2 δ2 的计算:
-
δ 2 = 1 m ∑ i = 1 m ( x i − μ ) 2 = 1 m ∑ i = 1 m ( x i 2 − 2 x i μ + μ 2 ) = ? 1 m ∑ i = 1 m x i 2 − μ 2 = 1 m ∑ i = 1 m x i 2 − ( 1 m ∑ i = 1 m x i ) 2 μ = 1 m ∑ i = 1 m x i , 而不是 μ = ∑ j = 1 n ∑ i = 1 m x i j 吗?( n 为节点个数, m 为每个节点的批量样本数) \delta^2=\frac{1}{m}\sum_{i=1}^m(x_i-\mu)^2=\frac{1}{m}\sum_{i=1}^m(x^2_i-2x_i\mu+\mu^2)=?\frac{1}{m}\sum_{i=1}^mx_i^2-\mu^2\\ =\frac{1}{m}\sum_{i=1}^mx_i^2-(\frac{1}{m}\sum_{i=1}^mx_i)^2\\ \mu=\frac{1}{m}\sum_{i=1}^mx_i,而不是 \mu=\sum_{j=1}^n\sum_{i=1}^mx_{ij}吗?(n为节点个数,m为每个节点的批量样本数) δ2=m1i=1∑m(xi−μ)2=m1i=1∑m(xi2−2xiμ+μ2)=?m1i=1∑mxi2−μ2=m1i=1∑mxi2−(m1i=1∑mxi)2μ=m1i=1∑mxi,而不是μ=j=1∑ni=1∑mxij吗?(n为节点个数,m为每个节点的批量样本数)
-
只需要在同步时算好 ∑ i = 1 m x i \sum_{i=1}^mx_i ∑i=1mxi 和 ∑ i = 1 m x i 2 \sum_{i=1}^mx_i^2 ∑i=1mxi2 即可。这里用一张图来描述这一过程。
-

-
-
-
BatchNorm、LayerNorm、InstanceNorm、GroupNorm、Weight Standardization
-
BatchNorm:batch方向做归一化,算NHW的均值,对小batchsize效果不好;BN主要缺点是对batchsize的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batchsize太小,则计算的均值、方差不足以代表整个数据分布;
-
LayerNorm:channel方向做归一化,算CHW的均值,主要对RNN,transformer作用明显;
-
InstanceNorm:一个channel内做归一化,算H*W的均值,用在风格化迁移;因为在图像风格化中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
-
GroupNorm:将channel方向分group,然后每个group内做归一化,算(C//G)H*W的均值;这样与batchsize无关,不受其约束。将channel分组,然后再做归一化, 在batchsize<16的时候, 可以使用这种归一化。
-
SwitchableNorm:将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
-
Weight Standardization:权重标准化,2019年约翰霍普金斯大学研究人员提出。
-

-
-
数据归一化是深度学习数据预处理非常关键的步骤,可以起到统一量纲,防止小数据被吞噬等作用。把所有数据都转化为[0,1]或者[-1,1]之间的数,其目的是取消各维数据间数量级差别,避免因为输入输出数据数量级差别较大而造成网络预测误差较大。
-
线性归一化:也称为最小-最大规范化、离散标准化,是对原始数据的线性变换,将数据值映射到[0,1]之间。离差标准化保留了原来数据中存在的关系,是消除量纲和数据取值范围影响的最简单方法。
-
x ′ = x − m i n ( x ) m a x ( x ) − m i n ( x ) x'=\frac{x-min(x)}{max(x)-min(x)} x′=max(x)−min(x)x−min(x)
- 比较适用在数值比较集中的情况。
-
零-均值规范化:也称标准差标准化,经过处理的数据的均值为0,标准差为1。转化公式为:
-
x ′ = x − μ δ x'=\frac{x-\mu}{\delta} x′=δx−μ
-
标准差分数可以回答这样一个问题:"给定数据距离其均值多少个标准差"的问题,在均值之上的数据会得到一个正的标准化分数,反之会得到一个负的标准化分数。
-
-
局部响应归一化
- 局部响应归一化LRN 是一种提高深度学习准确度的技术方法。LRN 一般是在激活、池化函数后的一种方法。该方法是由AlexNet网络提出,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。LRN层模仿了生物神经系统的“侧抑制”机制。
。该方法是由AlexNet网络提出,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。LRN层模仿了生物神经系统的“侧抑制”机制。
- 局部响应归一化LRN 是一种提高深度学习准确度的技术方法。LRN 一般是在激活、池化函数后的一种方法。该方法是由AlexNet网络提出,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。LRN层模仿了生物神经系统的“侧抑制”机制。
【归一化小记】,batchnorm,layernorm,IN,GN,分布式归一化...
news2026/2/14 3:33:54
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/364104.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【HTML】HTML 表单 ④ ( textarea 文本域控件 | select 下拉列表控件 )
文章目录一、textarea 文本域控件二、select 下拉列表控件一、textarea 文本域控件 textarea 文本域 控件 是 多行文本输入框 , 标签语法格式如下 :
<textarea cols"每行文字字符数" rows"文本行数">多行文本内容
</textarea>实际开发中 并不…
聚观早报 | 嘀嗒出行重启赴港IPO;饿了么到店业务将与高德合并
点击蓝字 / 关注我们今日要闻:嘀嗒出行重启赴港 IPO;饿了么到店业务将与高德合并;美团香港骑手月收入高达3.5万港元;腾讯或引进Meta旗下VR眼镜Quest 2;苹果将阻止用户免费装开测版iOS 17
嘀嗒出行重启赴港 IPO
港交所文…
Java企业开发学习笔记(2)利用组件注解符精简Spring配置文件
该文章主要为完成实训任务,详细实现过程及结果见【http://t.csdn.cn/iSeSH】 文章目录一、 利用组件注解符精简Spring配置文件1.1 创建新包1.2 复制四个类1.3 修改杀龙任务类1.4 修改救美任务类1.5 修改勇敢骑士类1.6 修改救美骑士类1.7 创建Spring配置文件1.8 创建…
【数据库】redis数据持久化
目录
数据持久化
一, RDB
1, 什么是RDB
2,持久化流程
3, 相关配置
案例演示:
4, 备份和恢复
1、备份
2、恢复
3,优势
4, 劣势
二,AOF
1,什么是A…
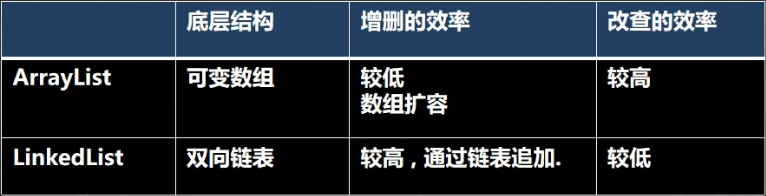
Java笔记026-集合/数组、Collection接口、ArrayList、Vector、LinkedList
集合集合的理解和好处保存多个数据使用的是数组,分析数组的弊端数组1、长度开始必须指定,而且一旦指定,不能更改2、保存的必须为同一类型的元素3、使用数组进行增加/删除元素的示意代码-比较麻烦Person数组扩容示意代码Person[] pers new Pe…
ChatGPT三个关键技术
情景学习(In-context learning) 对于一些LLM没有见过的新任务,只需要设计一些任务的语言描述,并给出几个任务实例,作为模型的输入,即可让模型从给定的情景中学习新任务并给出满意的回答结果。这种训练方式能…
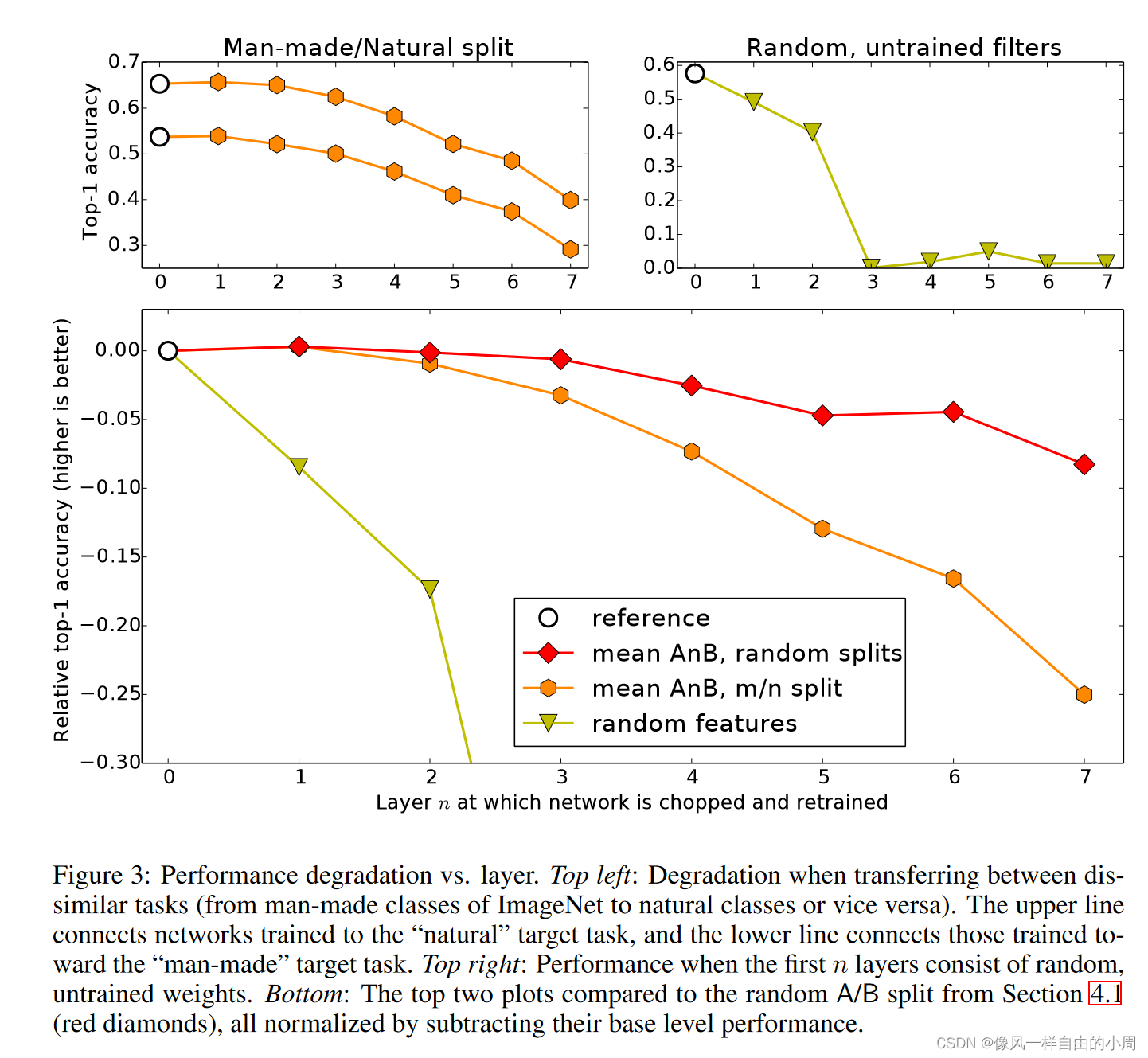
论文笔记:How transferable are features in deep neural networks? 2014年NIP文章
文章目录一、背景介绍二、方法介绍三、实验论证四、结论五、感想参考文献一、背景介绍
1.问题介绍: 许多在自然图像上训练的深度神经网络都表现出一个奇怪的共同现象:在第一层,它们学习类似于Gabor过滤器和color blobs的特征。这样的第一层特…
c++提高篇——list容器
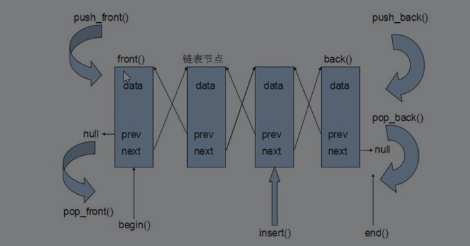
一、基本概念
功能:将数据进行链式存储 链表((list)是一种物理存储单元上非连续的存储结构,数据元素的逻辑顺序是通过链表中的指针链接实现的,链表由一系列结点组成。 结点的组成:一个是存储数据元素的数据域,另一个是存储下一个…
3DVR营销是什么?是否成为市场热门?
在当今市场经济环境中,营销对于在企业发展中的作用至关重要。市场是企业发展的战场,谁能在市场营销方面做得更好,就能够吸引公域平台流量、占据主流市场、开拓新局面从而稳定现有规模。这将确保企业不被市场淘汰,而是能够可持续性…
CSS(配合html的网页编程)
续上一篇博客,CSS是前端三大将中其中的一位,主要负责前端的皮,也就是负责html的装饰.一、基本语法规则也就是:选择器若干属性声明(选中一个元素然然后进行属性声明)CSS代码是放在style标签中,它可以放在head中也可以放在body中 ,可以放到代码的任意位置.color也就是设置想要输入…
如何描述元素与元素间的逻辑关系?
逻辑结构反映的是数据元素之间的关系,它们与数据元素在计算机中的存储位置无关,是数据结构在用户面前所呈现的形式。根据不同的逻辑结构来分,数据结构可分为集合、线性结构、树形结构和图形结构4种形式,接下来分别进行简要介绍。 …
宝塔搭建实战php源码云切程序转码m3u8生程序开源源码
大家好啊,我是测评君,欢迎来到web测评。 今天给大家分享一套php云切片转码的源码,分享自己的视频但是由于视频文件太大,服务器带宽太小,导致分享困难,部署这套系统后,就可以在上传视频后切成ts格…
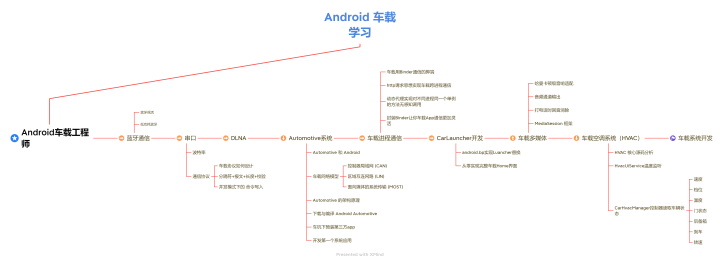
车机开发—【CarService启动流程】
汽车架构:车载HAL是汽车与车辆网络服务之间的接口定义(同时保护传入的数据):
车载HAL与Android Automotive架构:
Car App:包括OEM和第三方开发的AppCar API:内有包含CarSensorManager在内的AP…
5个有效的华为(HUAWEI)手机数据恢复方法
5个有效的手机数据恢复方法
华为智能手机中的数据丢失比许多人认为的更为普遍。发生这种类型的丢失有多种不同的原因,因此数据恢复软件的重要性。您永远不知道您的智能手机何时会在这方面垮台;因此,预防总比哀叹好,这就是为什么众…
通过 FTP 使用 Python 自动压缩网站图像
图像压缩对于技术SEO世界来说并不陌生,但是随着核心生命体征形式的网站性能是一个排名因素,现在是时候开始采取行动了。我已经做了几十次网站审计,我发现 80% 的网站性能问题都可以在图像或 JavaScript 下进行。当我看到图像是一个大问题时,我会欢呼,因为它是最容易解决的…
注意啦,面试通过后,别忘了教师资格证认定
所有要「教师资格证认定」教程的宝子们看过来面试合格的小伙伴都可以进行认定工作 . 认定时间 查询各省份认定公告,确定认定时间范围。以下是公告汇总网址(https://www.jszg.edu.cn/portal/qualification_cert/dynamics?id21691) 认定次数 每…
【jQuery】js实现文件浏览功能
1.说明
近期遇到一个浏览用户文件的需求,类似于访问百度网盘那样的列表,包含文件和文件夹,这个功能实现起来很简单,从服务器获取到的文件列表至少要有文件id、父级文件id、是否文件夹这三个字段
2.html设计
前端排版看你实际情…
x86架构设备的OpenWrt的空间扩容问题
openwrt固件是squashfs-combined-efi非exf4格式
直接将原有根分区扩容
用插件是:fdisk,losetup,resize2fs,blkid
df -h
fdisk -l
fdisk /dev/sda //进入fdisk分区管理工具注意fdisk后参数是磁盘名称,是要根据实际情况填写
fdisk /dev/sda //进入fdi…
【04-JVM面试专题-什么是双亲委派机制(父类委托机制)?如何打破双亲委派机制?双亲委派机制的优缺点?什么是沙箱安全机制呢?】
什么是双亲委派机制?如何打破双亲委派机制? JVM的双亲委派机制知道吗?怎么打破它呢?你看看自己掌握的怎么样呢? 什么是双亲委派机制?(父类委托机制)
检查某个类是否已经加载 自底向上,从Custom…
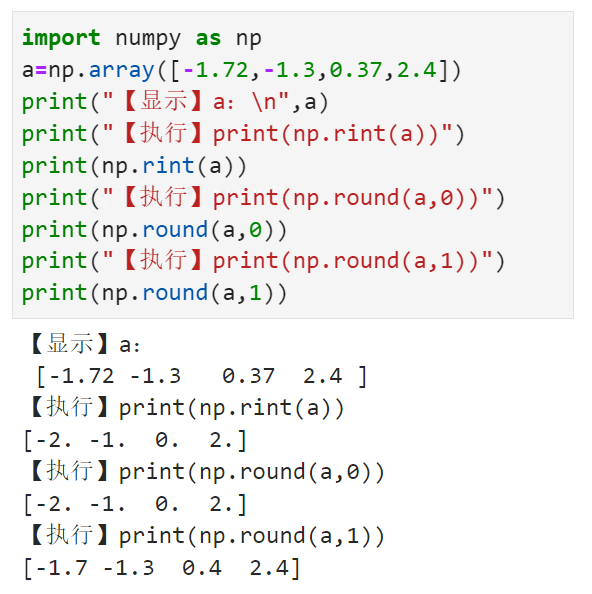
将数组中的每个元素四舍五入到指定的精度numpy.rint()
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 将数组中的每个元素 四舍五入到指定的精度 numpy.rint() 选择题 请问np.rint(a)的输出结果是? import numpy as np anp.array([-1.72,-1.3,0.37,2.4]) print("【显示】a:\n…