文章目录
- 1. 平衡二叉树的概念
- AVL树的插入
- AVL树查找效率
- AVL树的删除(了解)
- 2. C++代码
- 3. 考研数据结构代码仓库
1. 平衡二叉树的概念
二叉搜索树虽然可以提高搜索效率,但如果数据接近有序的话搜索二叉树的效率退化为链表了。为了解决这个问题,提出了AVL树。
向平衡二叉树中插入新节点,保证每个节点的高度差的绝对值小于等于1。降低树的高度,提高搜索效率。这种树称为AVL树
为了确定插入或者删除节点后,这棵树的高度差的绝对值,这里给树的每一个节点引入平衡因子。
每个节点的平衡因子=这个节点的右子树高度-这个节点的左子树高度。
所以根据AVL树的定义:当平衡因子变为2或-2时,需要调整AVL树
AVL树的插入
情况一:右单旋(新节点插入较高左子树的左侧)
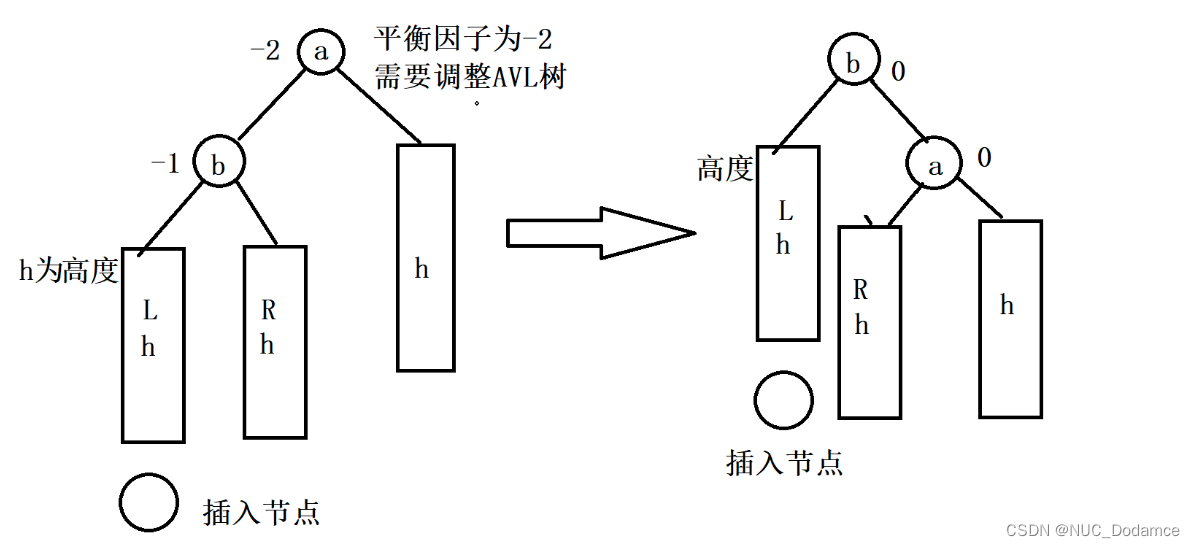
插入新节点后,b节点平衡因子为-1,a节点平衡因子为-2。
调整步骤:将a节点连接到b右节点,将原来b右子树连接到a左子树上,这样a,b节点的平衡因子又变回0
情况二:左单旋(新节点插入较高右子树的右侧)
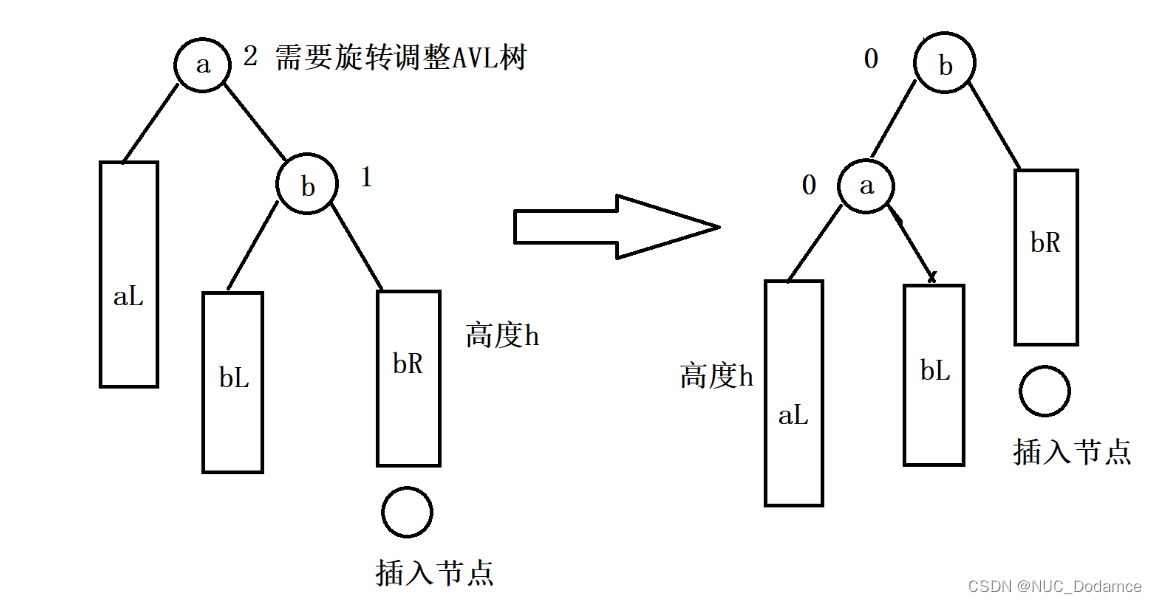
插入新节点后,b节点平衡因子为1,a节点平衡因子为2
旋转思路:将bL连接到a的右树上,a再连接到b的左树上。调整平衡因子a,b平衡因子都变为0,调整a,b节点父指针,调整树的根节点,处理子树的情况,细节和右单旋类似。这样a,b节点的平衡因子又变回0
情况三:左右双旋(新节点插入较高左子树的右侧)
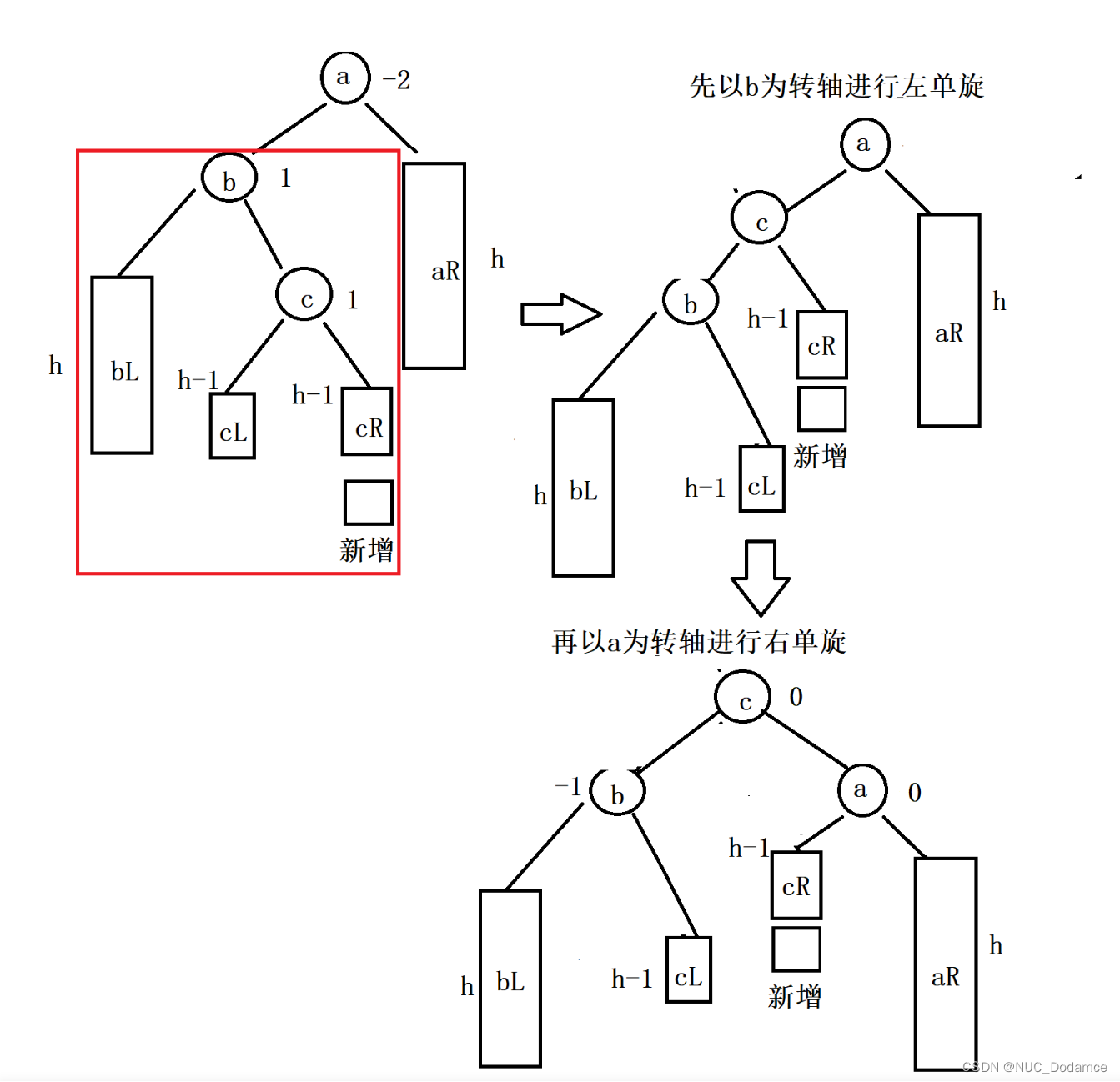
观察上图,相当于把c节点拆开c做根节点,c的左子树给b右树,c的右子树给a的左树。c的左子树连接b,c的右子树连接a。从而达到降低树的高度的目的。
根据上面的分析可知c在旋转后平衡因子一定为0.
如果新节点插入的位置在c的左子树上,经过旋转会到b的右子树上,b的平衡因子为0,a的平衡因子为1.
如果新节点插入的位置在c的右子树上,经过旋转会到a的左子树上,b的平衡因子为-1,a的平衡因子为0(如上图).
特殊情况:当b节点没有子树时,即这颗树只有cba这三个节点,此时a,b,c这三个节点的平衡因子都为0
情况四:右左双旋(新节点插入较高右子树的左侧)
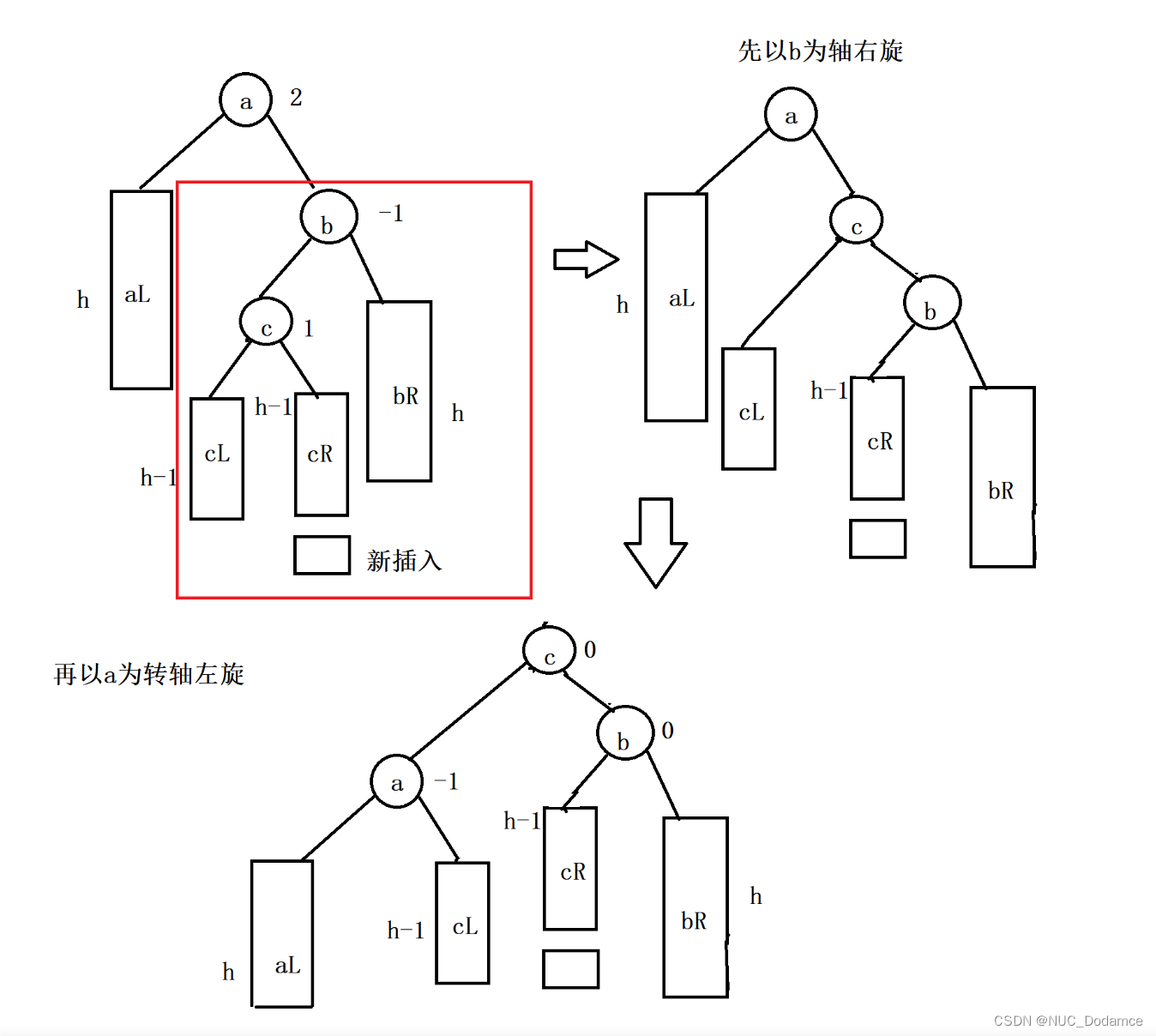
由上图可以看到a节点的平衡因子为2,b节点的平衡因子为-1时要进行右左双旋。
特点为:b节点进行右旋,a节点进行左旋。
AVL树查找效率
如果树高为h,最坏情况下,查找需要对比h次
平衡二叉树上任一结点的左子树和右子树的高度之差不超过1。
假设以n(h)表示深度为h的平衡树中含有的最少结点数。
n(0)=0此时是空树,n(1)=1此时树只有根节点,n(2)=2……
高度为h的平衡二叉树,最少节点个数为n(h)=n(h-1)+n(h-2)+1
所以9个节点的平衡二叉树i有四层,最坏需要对比4次就可以查找到对应元素
所以平衡二叉树的事件复杂度为树高O(logN)
AVL树的删除(了解)
AVL树的删除操作与插入类似;
- 首先先按照二叉搜索树的删除规则进行删除
- 之后向上更新平衡因子,如果遇到不平衡的情况和AVL树插入操作类似进行树结构的调整,调整规则完全相同
AVL树的删除,关键就是平衡因子的调整。调整完毕后,根据平衡因子的值,选择旋转方式,并向上进行传递。
我这里使用:每次删除后,从删除根节点开始调整平衡因子,如果失去了AVL树形状,进行反转,之后依次向上递归调整。类似后续遍历的方式。
从整棵树的最下方从头开始调整。
这个方法有个弊端,就是每次删除必须向上判断平衡因子是否正确,效率比较低
2. C++代码
BalanceTree类
#include <iostream>
#include <vector>
#include <algorithm>
struct Node
{
int _bf;
Node *_left;
Node *_right;
Node *_parent;
int _val;
Node(int val) : _bf(0), _left(nullptr), _right(nullptr), _parent(nullptr), _val(val) {}
};
class BalanceTree
{
Node *root;
public:
~BalanceTree() {}
void InorderDisplay()
{
_DisPlay(root);
std::cout << "\n";
}
BalanceTree(const std::vector<int> buff)
{
for (auto &num : buff)
{
insert(num);
}
}
bool insert(int val)
{
// 不允许值重复
if (root == nullptr)
{
root = new Node(val);
return true;
}
else
{
Node *prev = nullptr;
Node *cur = root;
while (cur != nullptr)
{
prev = cur;
if (cur->_val < val)
{
cur = cur->_right;
}
else if (cur->_val > val)
{
cur = cur->_left;
}
else
{
// 数据冗余
return false;
}
}
// cur==nullptr
cur = new Node(val);
if (prev->_val > val)
prev->_left = cur;
else
prev->_right = cur;
cur->_parent = prev;
// 更新平衡因子
while (prev != nullptr)
{
// 判断插入位置
if (prev->_left == cur)
prev->_bf--;
else if (prev->_right == cur)
prev->_bf++;
if (prev->_bf == 0)
{
break; // 插入后仍然是AVL树
}
else if (prev->_bf == -1 || prev->_bf == 1)
{
cur = prev;
prev = prev->_parent; // 这次插入影响高度,需要向上调整
}
else if (prev->_bf == -2 || prev->_bf == 2)
{
// 不是AVL树需要调整高度
if (prev->_bf == -2)
{
if (cur->_bf == -1)
{
// 右单旋
TurnRight(prev);
}
else if (cur->_bf == 1)
{
// 左右双旋
TurnLeftRight(prev);
}
}
else if (prev->_bf == 2)
{
if (cur->_bf == -1)
{
// 右左双旋
TurnRightLeft(prev);
}
else if (cur->_bf == 1)
{
// 左单旋
TurnLeft(prev);
}
}
}
}
return true;
}
}
// 判断一棵树是否是AVL树
bool isAVLTree()
{
return _isAVLTree(root);
}
void erase(int val)
{
_erase(val, root);
_adjust(root);
}
private:
void _adjust(Node *node)
{
// 后续遍历调整搜索二叉树为AVL树
if (node == nullptr)
{
return;
}
_adjust(node->_left);
_adjust(node->_right);
int leftHeight = _height(node->_left);
int rightHeight = _height(node->_right);
node->_bf = rightHeight - leftHeight;
if (node->_bf == 2 || node->_bf == -2)
{
Node *left = node->_left;
Node *right = node->_right;
if (node->_bf == -2)
{
if ((left != nullptr && left->_bf == -1) || (right != nullptr && right->_bf == -1))
{
// 右旋
TurnRight(node);
}
else if ((left != nullptr && left->_bf == 1) || (right != nullptr && right->_bf == 1))
{
// 左右双旋
TurnLeftRight(node);
}
}
else if (node->_bf == 2)
{
if ((left != nullptr && left->_bf == -1) || (right != nullptr && right->_bf == -1))
{
// 右左旋
TurnRightLeft(node);
}
else if ((left != nullptr && left->_bf == 1) || (right != nullptr && right->_bf == 1))
{
// 左旋
TurnLeft(node);
}
}
}
}
// 搜索二叉树删除方式
void _erase(int val, Node *&node)
{
// 删除节点值为val的节点,并且返回删除后这个节点的指针
if (node == nullptr)
{
return;
}
else
{
if (node->_val > val)
{
_erase(val, node->_left);
}
else if (node->_val < val)
{
_erase(val, node->_right);
}
else
{
if (node->_left == nullptr)
{
Node *del = node;
node = node->_right;
if (node != nullptr)
node->_parent = del->_parent;
delete del;
}
else if (node->_right == nullptr)
{
Node *del = node;
node = node->_left;
if (node != nullptr)
node->_parent = del->_parent;
delete del;
}
else
{
// 找要删除节点的后继
Node *right_min_node = node->_right;
while (right_min_node->_left != nullptr)
{
right_min_node = right_min_node->_left;
}
// 记录right_min_node这个节点的值,吧这个节点的值和node节点交换,在删除right_min_node这个节点即可
// right_min_node这个节点的左子树一定为空,在上面顶点流程会处理
int tmp = right_min_node->_val;
_erase(tmp, node->_right);
node->_val = tmp;
}
}
}
}
void _DisPlay(Node *root)
{
if (root == nullptr)
return;
_DisPlay(root->_left);
std::cout << root->_val << " ";
_DisPlay(root->_right);
}
int _height(Node *node)
{
if (node == nullptr)
return 0;
int leftHeight = _height(node->_left);
int rightHeight = _height(node->_right);
return std::max(leftHeight, rightHeight) + 1;
}
bool _isAVLTree(Node *node)
{
if (node == nullptr)
{
return true;
}
int leftHigh = _height(node->_left);
int rightHigh = _height(node->_right);
if (node->_bf != rightHigh - leftHigh)
{
std::cout << "ERROR:BF " << node->_bf << std::endl;
return false;
}
return std::abs(rightHigh - leftHigh) < 2 && _isAVLTree(node->_left) && _isAVLTree(node->_right);
}
/**
* 旋转代码结合博客流程对照
*/
// 右单旋
void TurnRight(Node *node)
{
Node *left = node->_left;
Node *right = left->_right;
node->_left = right;
if (right != nullptr)
{
right->_parent = node;
}
left->_right = node;
Node *parent = node->_parent; // 原父母
node->_parent = left;
// 修改平衡因子
node->_bf = 0;
left->_bf = 0;
if (node == root)
{
// 旋转根节点
root = left;
root->_parent = parent;
}
else
{
left->_parent = parent;
if (parent->_left == node)
{
parent->_left = left;
}
else
{
parent->_right = left;
}
}
}
// 左单旋
void TurnLeft(Node *node)
{
Node *right = node->_right;
Node *left = right->_left;
node->_right = left;
if (left != nullptr)
{
left->_parent = node;
}
right->_left = node;
Node *parent = node->_parent;
node->_parent = right;
node->_bf = 0;
right->_bf = 0;
if (node == root)
{
node = right;
right->_parent = parent;
}
else
{
right->_parent = parent;
if (parent->_left == node)
{
parent->_left = right;
}
else
{
parent->_right = right;
}
}
}
// 左右双旋
void TurnLeftRight(Node *node)
{
Node *left = node->_left;
Node *right = left->_right;
TurnLeft(left);
TurnRight(node);
// 调整平衡因子
if (right->_bf == 1)
{
// 新节点插入到right节点的右子树
right->_bf = 0;
left->_bf = -1;
node->_bf == 0;
}
else if (right->_bf == -1)
{
// 新节点插入到right节点的左子树上
right->_bf = 0;
left->_bf = 0;
node->_bf = 1;
}
else if (right->_bf = 0)
{
right->_bf = 0;
left->_bf = 0;
node->_bf = 0;
}
}
// 右左双旋
void TurnRightLeft(Node *node)
{
Node *right = node->_right;
Node *left = right->_left;
TurnRight(right);
TurnLeft(node);
if (left->_bf == 1)
{
left->_bf = 0;
right->_bf = 0;
node->_bf = -1;
}
else if (left->_bf == -1)
{
left->_bf = 0;
right->_bf = 1;
node->_bf = 0;
}
else if (left->_bf = 0)
{
left->_bf = 0;
right->_bf = 0;
node->_bf = 0;
}
}
};
测试代码:
#include "BalanceTree.h"
using namespace std;
int main(int argc, char const *argv[])
{
BalanceTree tree({3, 4, 2, 5, 6, 1, 7});
tree.InorderDisplay();
std::cout << tree.isAVLTree() << std::endl;
tree.erase(4);
tree.InorderDisplay();
std::cout << tree.isAVLTree() << std::endl;
tree.erase(5);
tree.InorderDisplay();
std::cout << tree.isAVLTree() << std::endl;
return 0;
}
运行结果:
3. 考研数据结构代码仓库
考研数据结构代码仓库