1.题目

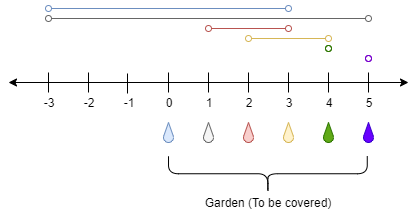
在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, …, n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的最少水龙头数目。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

示例 1：

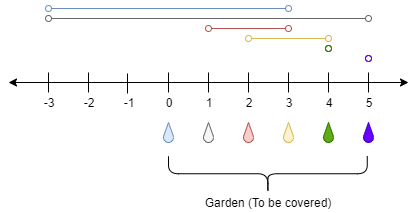
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：
输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

提示：
1 <= n <= 10⁴
ranges.length == n + 1
0 <= ranges[i] <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-number-of-taps-to-open-to-water-a-garden

2.思路

（1）动态规划
思路参考本题官方题解。

3.代码实现（Java）

//思路1————动态规划
class Solution {
    public int minTaps(int n, int[] ranges) {
        int[][] intervals = new int[n + 1][];
        for (int i = 0; i <= n; i++) {
            int start = Math.max(0, i - ranges[i]);
            int end = Math.min(n, i + ranges[i]);
            intervals[i] = new int[]{start, end};
        }
        /*
            此时题目转换为：
            从 [start0, end0]、[start1, end1]、...、[startn, endn] 中选出最少数目的区间，使得它们可以覆盖 [0, n]
         */
        //将所有区间按照起点进行升序排序
        Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
        //设 dp[i] 表示覆盖区间 [0, i] 所需要的最少的区间数目
        int[] dp = new int[n + 1];
        Arrays.fill(dp, Integer.MAX_VALUE);
        dp[0] = 0;
        for (int[] interval : intervals) {
            int start = interval[0];
            int end = interval[1];
            if (dp[start] == Integer.MAX_VALUE) {
                return -1;
            }
            for (int j = start; j <= end; j++) {
                dp[j] = Math.min(dp[j], dp[start] + 1);
            }
        }
        return dp[n];
    }
}