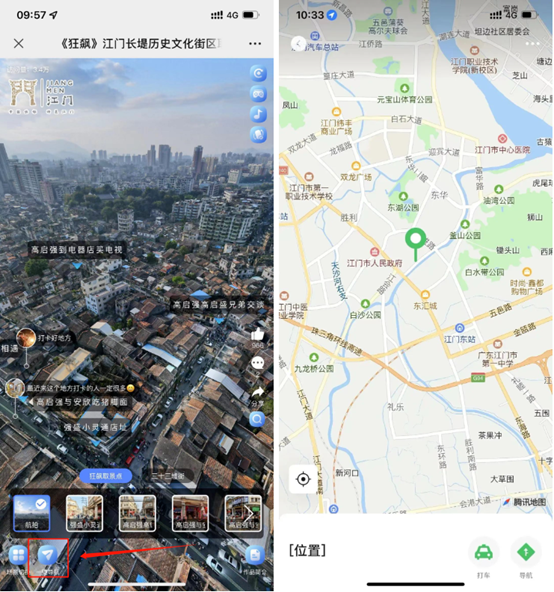
目录
- 简介
- UKF滤波
- 滤波流程和公式
- MATLAB程序
- 结论
简介
本文接着分享位姿跟踪和滤波算法中用到的一些常用程序,希望为后来者减少一些基础性内容的工作时间。以往分享总结见文章:位姿跟踪 | 相关内容目录和链接总结(不断更新中~~~)
本文分享无迹卡尔曼滤波(UKF)算法的一些基本公式和MATLAB程序。
UKF滤波
首先简单介绍一下UKF滤波的优点和公式。本文偏工程性介绍,因此UKF的原理就不再过多介绍了。
滤波流程和公式
首先需要明确滤波模型中的状态变量、状态方程和测量方程。
状态变量:x=[ ]
状态方程:x(k+1) = f(x(k))
测量方程:z(k+1) = h(x(k+1))
很简单对吧?
接着求解介绍求解流程 :
-
相比于一般的卡尔曼滤波,UKF算法增加了两次无迹变换,公式为:

权重和方差计算公式为:

-
Sigma点传播:

- 计算x的预测值和协方差矩阵:

4. 得到一组新的Sigma点:

5. 代入观测方程中,得到测量量的预估值:
![]()
- 获得观测量的预测值和协方差矩阵:

- 更新状态变量和协方差矩阵:



另外,每次写论文画卡尔曼流程图中,都找不到参考的模板。我自己画了个滤波流程图,不一定符合每个人的审美,以备参考:

MATLAB程序
MATLAB程序如下,包括main.m函数和ukf.m函数:
main.m
P=[]
Q=[]
R=[]
f=@(x)[]
h=@(x)[]
z_msm = []
x0=[]
ux = x0;
% 滤波初始值
for k=2:n_before_colli
[xukf(:,k), P] = ukf(f_before,ux,P,h_before,z_pre(:,k),Q,R);
ux=xukf(:,k); % k时刻的状态变量估计值
end
ukf.m
function [X,P]=ukf(ffun,X,P,hfun,Z,Q,R)
x_temp = X;
L=numel(X);
m=numel(Z);
% alpha=1e-2;
alpha = 2;
ki=0;
beta=2;
% alpha = 2;
% ki=3-L;
% beta=2;
lambda=alpha^2*(L+ki)-L;
c=L+lambda;
Wm=[lambda/c 0.5/c+zeros(1,2*L)];
Wc=Wm;
Wc(1)=Wc(1)+(1-alpha^2+beta);
c=sqrt(c);
Xsigmaset=sigmas(X,P,c);
[X1means,X1,P1,X2]=ut(ffun,Xsigmaset,Wm,Wc,L,Q);
[Zpre,Z1,Pzz,Z2]=ut(hfun,X1,Wm,Wc,m,R);
Pxz=X2*diag(Wc)*Z2';
K=Pxz*inv(Pzz);
X=X1means+K*(Z-Zpre);
P=P1-K*Pxz';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%d%%%%%
% UT
function [Xmeans,Xsigma_pre,P,Xdiv]=ut(fun,Xsigma,Wm,Wc,n,COV)
LL=size(Xsigma,2);
Xmeans=zeros(n,1);
Xsigma_pre=zeros(n,LL);
for k=1:LL
Xsigma_pre(:,k)=fun(Xsigma(:,k));
Xmeans=Xmeans+Wm(k)*Xsigma_pre(:,k);
end
Xdiv=Xsigma_pre-Xmeans(:,ones(1,LL));
P=Xdiv*diag(Wc)*Xdiv'+COV;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% sigma
function Xset=sigmas(X,P,c)
A = c*chol(P)';
Y = X(:,ones(1,numel(X)));
Xset = [X Y+A Y-A];
结论
PS:为了避免论文查重,以下内容从正文中剪切。
UKF的优点:






![[ vulhub漏洞复现篇 ] Drupal XSS漏洞 (CVE-2019-6341)](https://img-blog.csdnimg.cn/1bb0445177ce4a708649caac6b1dff00.png)