零. 前言
堆作为一种重要的数据结构,在面笔试中经常出现,排序问题中,堆排序作为一种重要的排序算法经常被问道,大顶堆小顶堆的应用经常出现,经典的问题TopN问题也是堆的重要应用,因此,了解并掌握这种数据结构是很必要的。
一. 堆的数据结构
1.由树而来
堆的数据结构可以看作是一种由数组实现的抽象完全二叉树,通过大顶堆或者小顶堆,来达到快速找到一新数据在整个堆结构中的应有位置,继而来实现排序、TopN问题或者log级别的算法要求。
完全二叉树,就是在一棵树中,元素从从上到下,从左到右依次变满,不会出现一个节点的左子节点不存在而右子节点存在的情况。
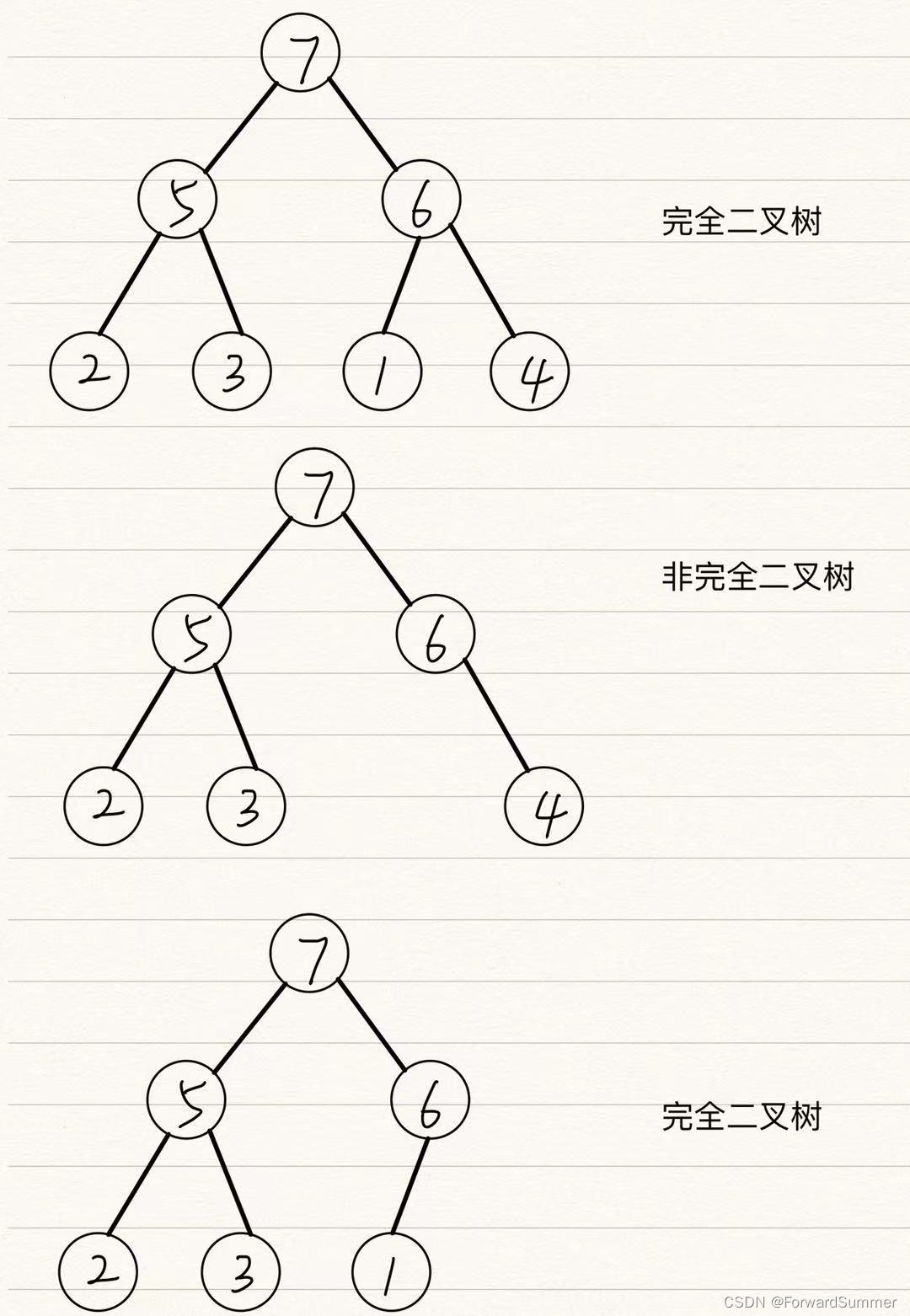
2.大顶堆
在一个大顶堆中,根节点的值比左右子树都要大(可以等于),在所有子树中都成立,但注意此时,左右子节点的大小并没有进行比较,所以是未知。
一个典型的大根堆案例:
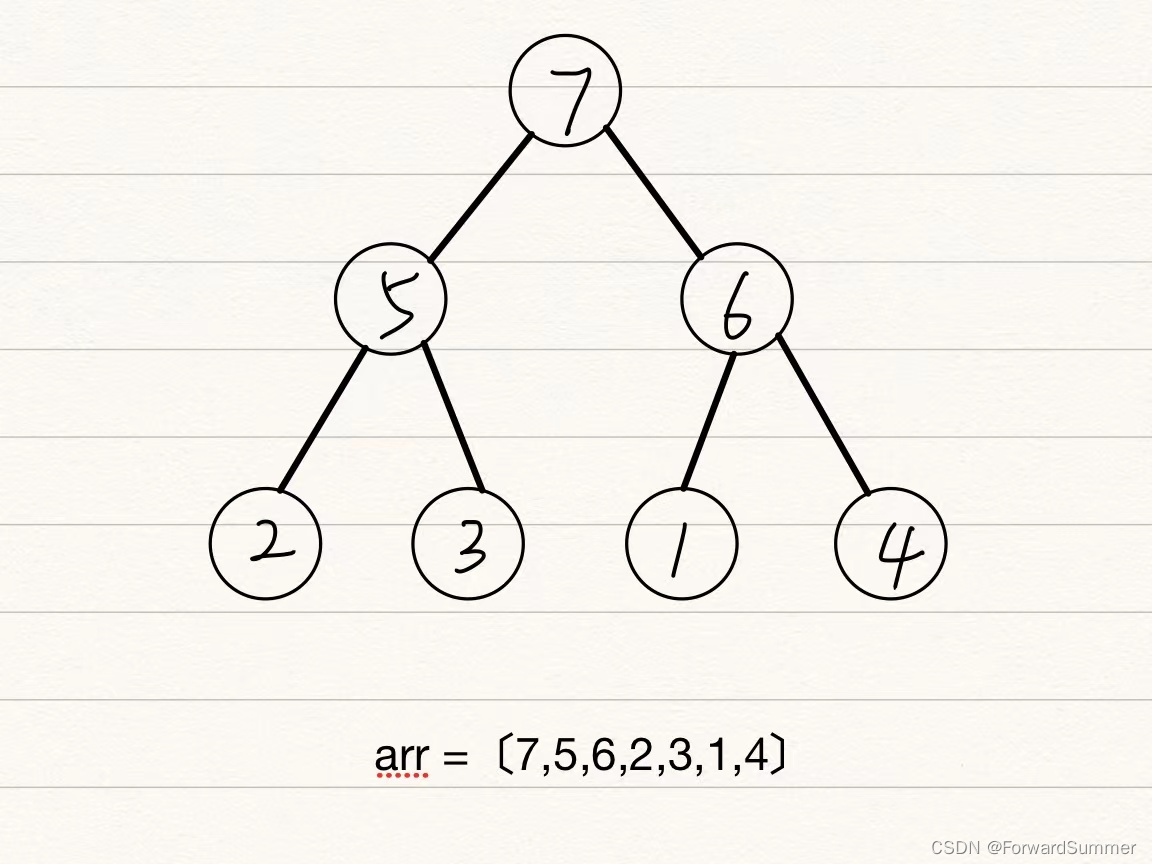
上图中的二叉树中的数值对应在数组中就是arr=[7,5,6,2,3,1,4],可以看作是树的层序遍历,从上到下,从左到右依次填满
3.小顶堆
在一个小顶堆中,根节点的值比左右子树都要小(可以等于),在所有子树中都成立,但注意此时,左右子节点的大小并没有进行比较,所以是未知。
案例同上,只不过大小相反,不再赘述。
4.数组实现堆中的对应关系
由数组实现方法中,会有数组下标和堆的抽象完全二叉树的对应关系,即数组中的第i元素在堆的哪个位置,或者说,堆中的元素映射在数组是哪个位置。
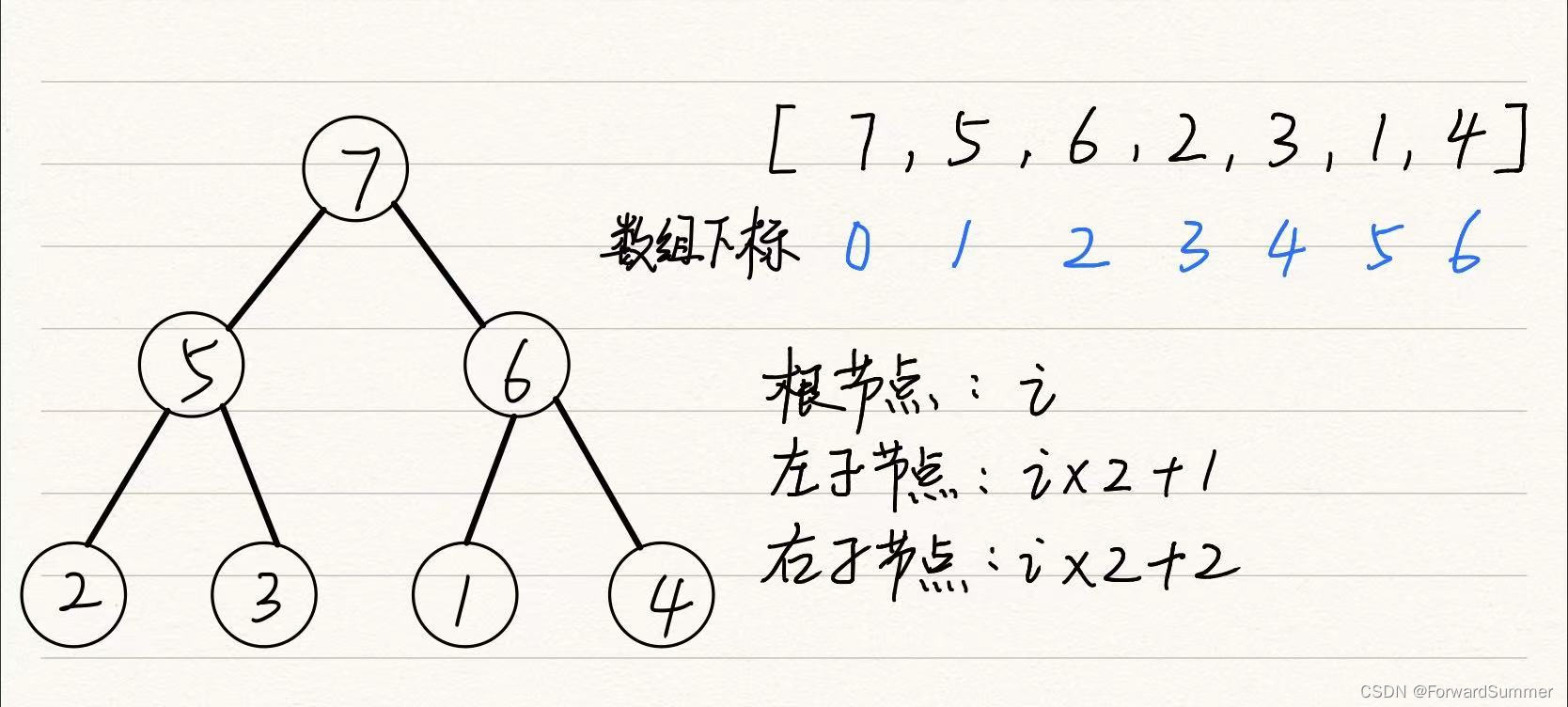
对于一个根节点i,它的左子节点是i*2+1,它的右子节点是i*2+2(如果存在的话,在实际中,可能左右子节点都不存在,会超出数组的实际长度,需提前判断)。
在下方的案例,元素6的下标在数组中对应2,2*2+1=5,数组中5对应的元素是1,而右子节点的元素是4,是一一对应的,而如果知道左子节点,或者右子节点,也可以反过来求根节点的在数组中的位置,对于一个左右子节点i,(i-1)/2即是根节点。
二. 堆构建
1.堆的构建过程
在手动构建堆的过程中,可以用以下的方式来手动构建一个堆【1】,默认为大顶堆:
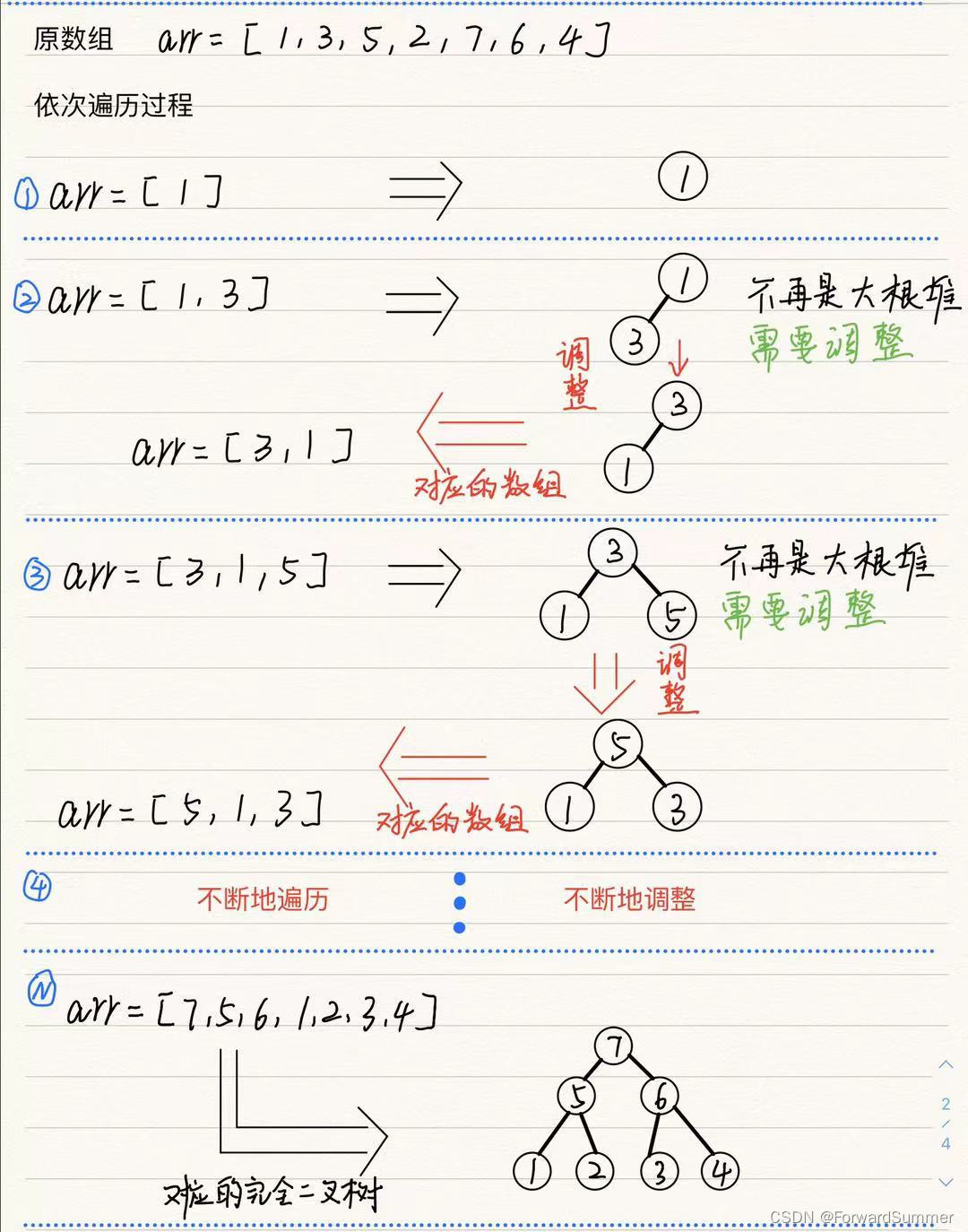
在整个堆的构建过程中,就是
(1)依次添加每个元素
(2)比较新添加的元素是否比根节点大(默认为大顶堆)
(3)如果新加入的子节点比根大就进行交换,然后一直向上换,直到不比父节点大,或者到达终点(在数组中即是0的位置)
整个过程是从底向上的过程,可以理解为上窜,上浮过程。
2.代码
class Solution {
public int[] newarrtoeHeap(int[] nums) {
return MakeHeap(nums);
}
public int[] MakeHeap(int[] nums){
int index = 0;
for(int i = 0; i < nums.length; i++){
HeapInsert(nums,index++);
}
}
public void HeapInsert(int[] nums, int index){
int root = (index-1)/2;
while(nums[root] < nums[index]){
swap(nums,root,index);
index = root;
root = (index-1)/2;
}
}
public void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}三. 利用堆进行排序
1.排序过程
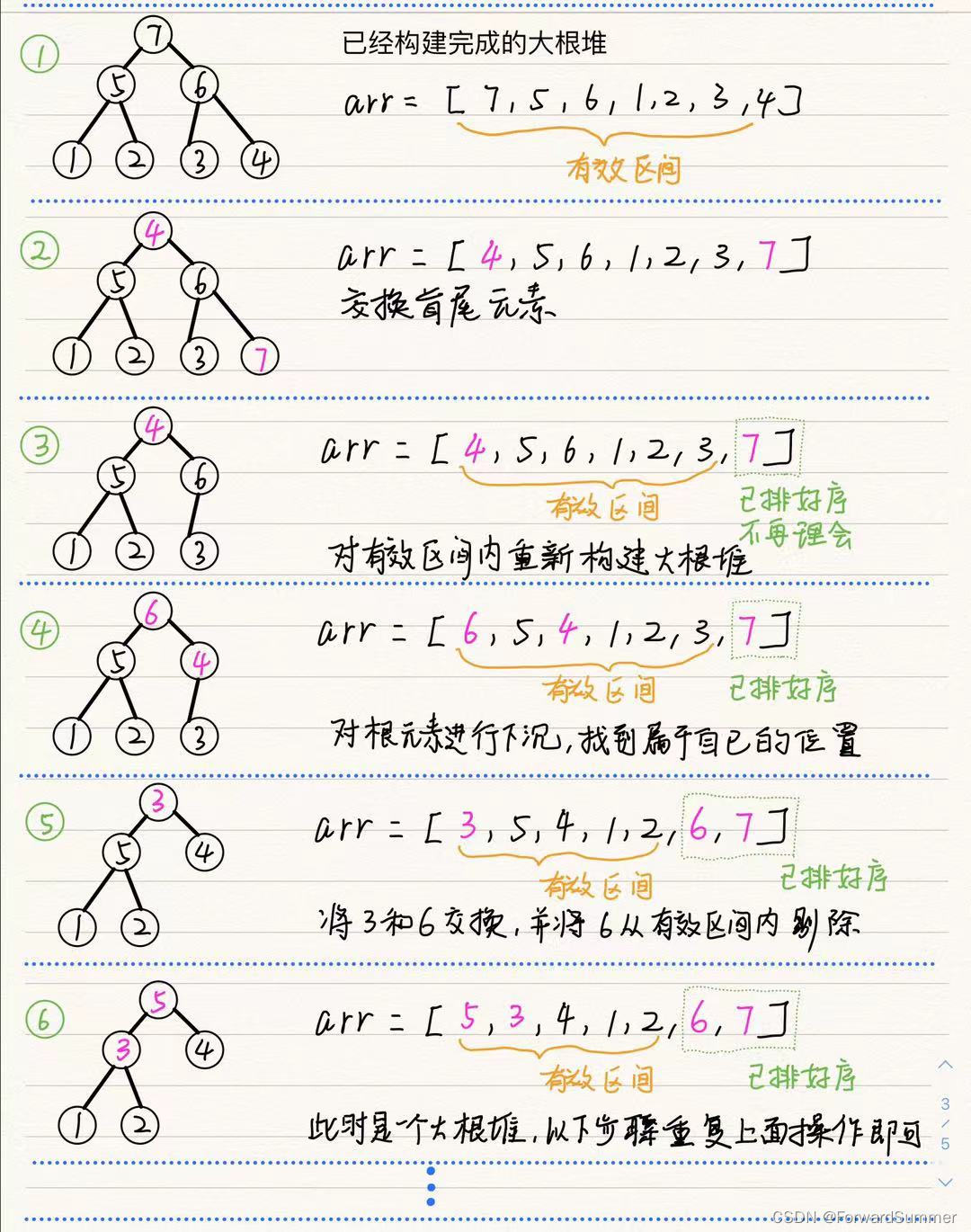
在第二章节中,对于一个已经构建好的堆来说,需要利用已经构建好的堆来进行排序,排序的整体过程如下:
(1)对于已经构建好的大根堆来说,数组最左边的元素即是数组中的最大值,把它取出即可
(2)然而取出之后,树不再是一颗完整的树,此时不利于后续操作(如果从左或者右取一个大元素放到根元素位置,那么后面的元素都要替换),所以此时可以把最左边的元素和最右边的元素交换,那么,最大的元素就是最右边的元素,缩减此时的有效区域即可
(3)此时虚拟的完全二叉树的根元素是从数组最右边提取的,大小位置,此时三个元素(新根元素,左子节点,右子节点需要进行比较)选出最大值作为根元素,新根元素不断和左右子节点比较直到找到属于自己合适的位置
(4)不断重复上述步骤,每次选出当前区间最大值,剔除最大值,区间从右向左不断缩减
利用第二章节的案例做具体的排序过程:
2.代码
class Solution {
public int[] sortArray(int[] nums) {
return HeapSort(nums);
}
public int[] HeapSort(int[] nums){
int index = 0;
for(int i = 0; i < nums.length; i++){
HeapInsert(nums,index++);
}
int sum = nums.length;
swap(nums,0,--sum);
while(sum > 0){
Heaptify(nums,0,sum);
swap(nums,0,--sum);
}
return nums;
}
public void HeapInsert(int[] nums, int index){
int root = (index-1)/2;
while(nums[root] < nums[index]){
swap(nums,root,index);
index = root;
root = (index-1)/2;
}
}
public void Heaptify(int[] nums,int temp, int sum){
int left = temp * 2 +1;
int right = left +1;
while(left < sum){
int max = right < sum ? (nums[left] < nums[right] ? right : left) : left;
max = nums[max] < nums[temp]? temp : max;
if(max == temp) break;
swap(nums,max,temp);
temp = max;
left = temp * 2 +1;
right = left +1;
}
}
public void swap(int[] nums, int i, int j){
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}以上的步骤都可以归结为:
(1)交换(首尾交换)
(2)下沉(新元素找到自己的位置)
(3)重复交换和下沉步骤
以上的步骤在代码中体现为下跳,下沉过程,对应在代码中为Heaptify()方法。
第二章节和第三章节的上浮和下沉操作配合即可完成排序过程。
3.堆排序的时间、空间复杂度、是否稳定
堆排序的最好时间复杂度、最坏时间复杂度和平均时间复杂度都是,在构建堆和重构堆的过程中,寻找目标元素或者为目标元素寻找恰当位置都是翻层寻找(*2)。
空间复杂度,只需要额外的swap函数辅助即可。
堆排序为不稳定排序,在重构堆的过程中会改变前后相同元素的原本位置。
四. Java PriorityQueue
在Java中,一个堆可以用PriorityQueue类来实现,默认为小根堆,如果需要大根堆,可以进行重排序。
PriorityQueue<Integer> queue = new PriorityQueue<>();重排序,可以用lambda表达式
PriorityQueue<Integer> queue = new PriorityQueue<>((v1,v2) -> v2-v1);或者重写Comparator比较器
class minHeap implements Comparator<Integer>{
public int compare(Integer m1,Integer m2){
return m1 - m2;
}
}
PriorityQueue<Integer> minheap = new PriorityQueue<>(new minHeap());
class maxHeap implements Comparator<Integer>{
public int compare(Integer m1,Integer m2){
return m2 - m1;
}
}
PriorityQueue<Integer> maxheap = new PriorityQueue<>(new maxHeap());具体使用,可以参考如下文章:
数据结构_堆_Java中的实现类
五. 堆排序、topN、PriorityQueue相关问题
1. leetcode 912 排序数组
给你一个整数数组nums,请你将该数组升序排列。
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
不再赘述,参考第三章节2. 剑指 Offer 40. 最小的k个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
暴力解法
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
int[] vec = new int[k];
Arrays.sort(arr);
for (int i = 0; i < k; ++i) {
vec[i] = arr[i];
}
return vec;
}
}大根堆
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
int[] ans = new int[k];
if(k == 0) return ans;
PriorityQueue<Integer> queue = new PriorityQueue<>((v1,v2) -> v2-v1);
for(int i : arr){
if(queue.size() < k){
queue.offer(i);
}
else{
if(queue.peek() > i){
queue.poll();
queue.offer(i);
}
}
}
int index = 0;
while(!queue.isEmpty()){
ans[index++] = queue.poll();
}
// int idx = 0;
// for(int num: queue) {
// ans[idx++] = num;
// }
return ans;
}
}本题小结:(1)此题是堆排序的典型应用案例,利用堆的性质来找到前k个大的数,或者前k个小的数
3. leetcode 347 前K个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
class Solution {
public List<Integer> topKFrequent(int[] nums, int k) {
// 使用字典,统计每个元素出现的次数,元素为键,元素出现的次数为值
HashMap<Integer,Integer> map = new HashMap();
for(int num : nums){
if (map.containsKey(num)) {
map.put(num, map.get(num) + 1);
} else {
map.put(num, 1);
}
}
// 遍历map,用最小堆保存频率最大的k个元素
PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {
@Override
public int compare(Integer a, Integer b) {
return map.get(a) - map.get(b);
}
});
for (Integer key : map.keySet()) {
if (pq.size() < k) {
pq.add(key);
} else if (map.get(key) > map.get(pq.peek())) {
pq.remove();
pq.add(key);
}
}
// 取出最小堆中的元素
List<Integer> res = new ArrayList<>();
while (!pq.isEmpty()) {
res.add(pq.remove());
}
return res;
}
}本题小结:(1)此题是和上体思路一样 ,不过需要首先求频率,在得到频率之后和上题解法如出一辙。
六. 参考来源
【1】b站 左程云 一周刷爆LeetCode p5
【2】leetcode yukiyama 十大排序从入门到入赘