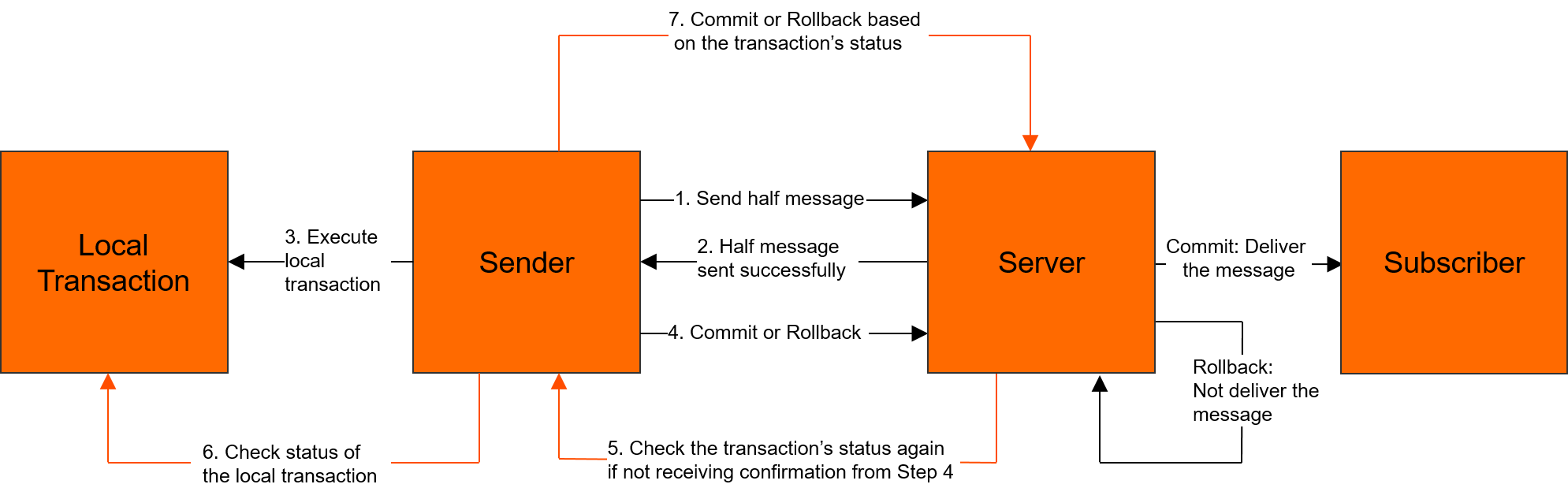
开学第一周,晚上属实作业有点乱
于是就拖更了一周

今天我们来讲解一下图论最短路径算法中
最简单
最清晰易懂
同时时间复杂度最高的算法
它的时间复杂度能达到O(VE)(点的数量*边的数量)
在学习Bellman-Ford之前,你需要先学会链式前向星
大家可以上网或者其他途径自行查阅一下
原理
这个算法是对图进行v-1次松弛操作(v为点的数量)
完了?
啊 完了

松弛看不懂没事
继续往下看
正式开始讲原理:
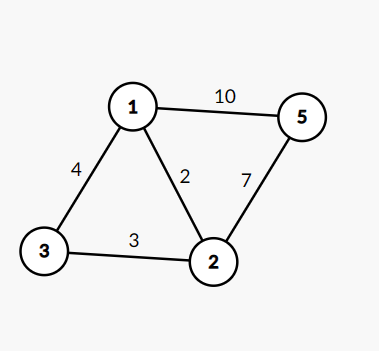
日常建个小图
有没有权值无所谓,没有权值就当作1
假设我们要求1点到5点的最短路径
第一步:把1连接的所有边的目标点更新最短路径路径
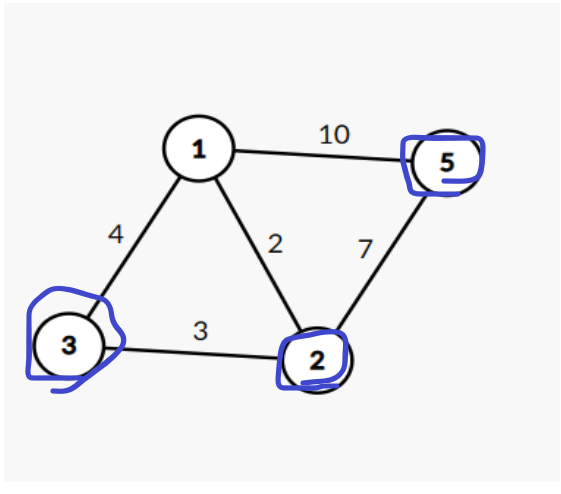
最短路径更新成现在这样
现在更新2的
这是可以发现,1到5的路程可以更新了
2+7<10
所以更新
然后剩下的就没什么可更新的了
这样算出来,1到5的最短路程就是9
上面一套流程,就是我们用贝尔曼福特算法的过程
而2+7<10这步,就叫做松弛操作
松弛N-1次,每次都遍历每个点的每条边,能松则松,不能松就不松
没错 贝尔曼福特还是这么简单
但这也造成了他时间复杂度贼高
就比如上图
3的松弛根本没用,也造成了时间上的问题
如果n<=10^6
那浪费的时间不可设想
另外 它还有一个优点
就是能处理负权环
怎么处理呢?
先来看下普通代码
# include <iostream>
# include <cstdio>
# include <cmath>
# include <cstring>
using namespace std;
# define int long long
# define N 10005
# define M 10005
int s,t,n,m,m2;
double f[N];
struct node{
int x,y;
}a[N];
struct node2{
int to,next;
double w;
}e[M];
int adj[N];
void add(int u,int v,double w2){
m2++;
e[m2].to=v;
e[m2].w=w2;
e[m2].next=adj[u];
adj[u]=m2;
return ;
}
void relax(int u,int v,double w2){
if (f[v]>f[u]+w2){
f[v]=f[u]+w2;
}
return ;
}
void ford(){
memset(f,0x7f7f,sizeof(f));
f[s]=0;
for (int i=1;i<=n-1;i++){
for (int j=1;j<=n;j++){
for (int k=adj[j];k;k=e[k].next){
int l=e[k].to;
relax(j,l,e[k].w);
}
}
}
return ;
}
signed main(){
ford();
printf("%.2lf",f[t]);
return 0;
}
本代码编写的是从s到t的最短路径,所以f[i]表示s到i的最短路径
解决下刚才的问题:负权环怎么解决
因为我们是n-1次松弛操作
在这种情况下,保证能把这个图的最短路径求出来
而负权环什么意思?他不可能有最短路径
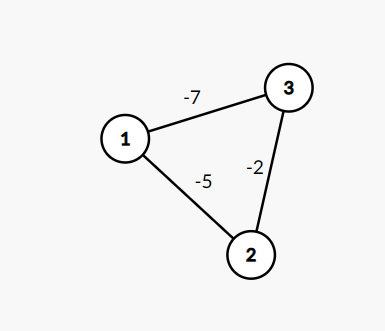
就是这个样子了
他每绕一圈,路径都-14
所以无限循环求不出
要想检测这种情况
就要松弛n次,如果第n次还有可以能松弛的
那说明就是负权环
有些同学就要问了
f数组不是动态规划里的吗?而且这个松弛操作为什么看上去这么像动态规划的状态转移方程啊?
没错你的直觉是正确的

自己的算法用自己的成就 天经地义()
今天的Bellman-Ford算法的讲解就到这里
如果还有哪些问题或不懂的地方 随时可以评论