【算法基础】一维前缀和 + 二维前缀和

news2025/2/24 21:23:47

在这里插入图片描述

👦个人主页：Weraphael
✍🏻作者简介：目前正在学习c++和算法
✈️专栏：【C/C++】算法
🐋 希望大家多多支持，咱一起进步！😁
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎评论💬 点赞👍🏻 收藏 📂 加关注😍

一、一维前缀和

1.1 什么是一维前缀和

前缀和就是新建一个数组，数组中保存的是原数组前n项的和

【举个例子】

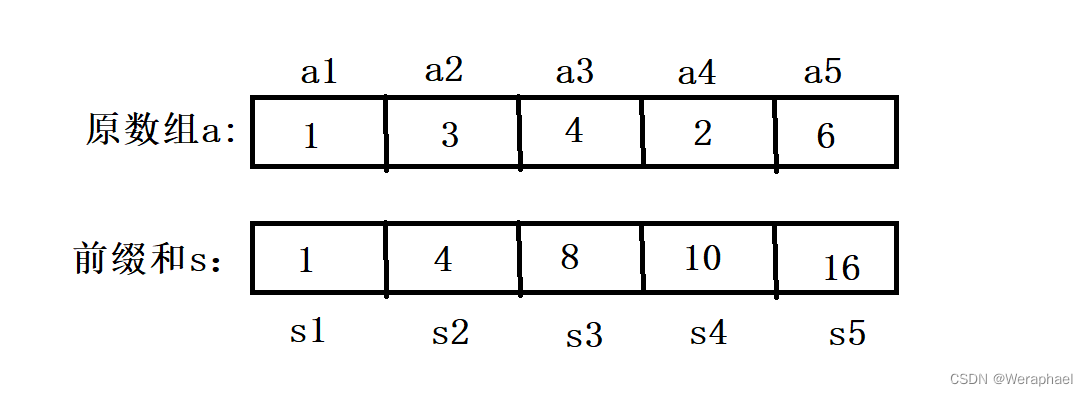
S_n = a₁+a₂+a₃+…a_n， S_n就是数列的前缀和（下标一定要从1开始，后面会讲解原因）

在这里插入图片描述

1.2 如何求Sn

我们可以利用上面的图来找找规律

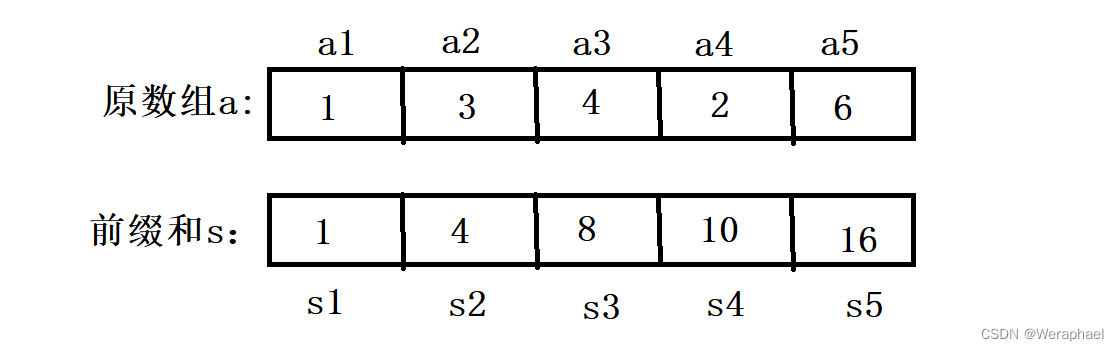
在这里插入图片描述

S₁ = a₁
S₂ = a₁ + a₂ = S₁ + a₂
S3 = a₁ + a₂ + a₃ = S₂ + a₃
S₄ = a₁ + a₂ + a₃ + a₄ = S₃ + a₄
S₅ = a₁ + a₂ + a₃ + a₄ + a₅ = S₄ + a₅
这一套下来，前缀和的公式很明显就是：S_i = S_i-1 + a_i

【代码】

for (int i = 1;i <= n;i++)
{
	s[i] = s[i-1] + a[i];
}

1.3 用途

能快速求出数列中某一段的和，时间复杂度为O(1)

还是要利用这幅图

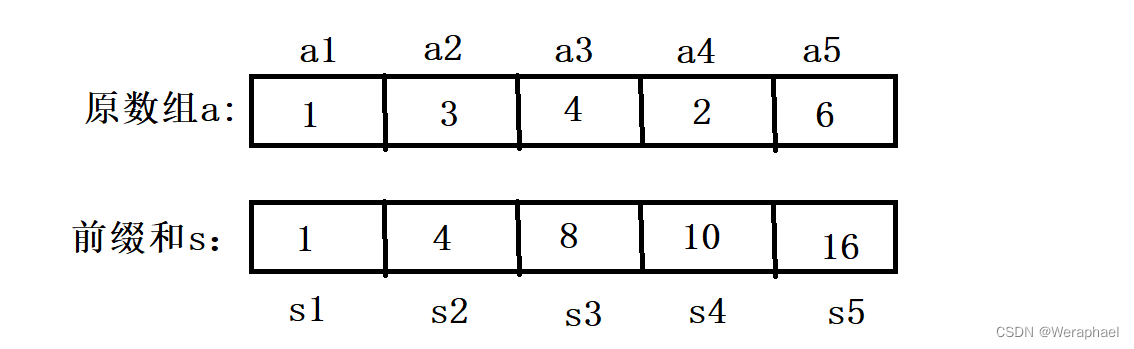
在这里插入图片描述
假设我们要计算原数组a中区间[2,4]的和，我们就可以用S₄ - S₁，

在这里插入图片描述

总结：假设日后题目要求区间[l,r]的和，其实也能循环遍历，不过时间复杂度是O(N)，而前缀和的时间复杂度是O(1)
计算区间[l,r]的和，其公式为S_r - S_l-1

1.4 代码模板

#include <iostream>
using namespace std;

const int N = 100010;
int a[N],s[n];

int main()
{
    int n; //n - 原数组元素的个数
    scanf("%d",&n);
    
    //输入原数组
    for (int i = 1;i <= n;i++) 
    {
        scanf("%d",&a[i]);
    }
    
    //前缀和公式
    for (int i = 1;i <= n;i++)
    {
        s[i] = s[i - 1] + a[i];
    }
    
    //以下是计算某段区间的和
    int l,r;
    scanf("%d%d",&l,&r);
    printf("%d\n",s[r] - s[l - 1]);
    
    return 0;
}

1.5 细节问题

首先，下标从1开始就是为了定义S₀，就拿前缀和公式来说，S[i] = S[i-1] + a[i]，当i = 1时，出现了S₀，而S₀要及时置为0，原因是为了统一。举个例子，假设要计算区间[1,10]之间的和，明眼就能看出是要计算S₁₀，而为了达到统一计算的效果，S₁₀ - S₀ = S₁₀ - 0.
为什么我在代码中没有定义S[0]=0，原因是我将s[N]定成了全局变量，而全局变量有一个特点：默认初始化为0！

二、二维前缀和

2.1 用途

目的是求出一个矩阵中某一个小矩阵的和

2.2 前缀和S[i][j]求法

大家画图可能会更加容易理解点，假设点（i，j）在矩阵的正中心，S[i][j] 即为黄色部分所有数的的和

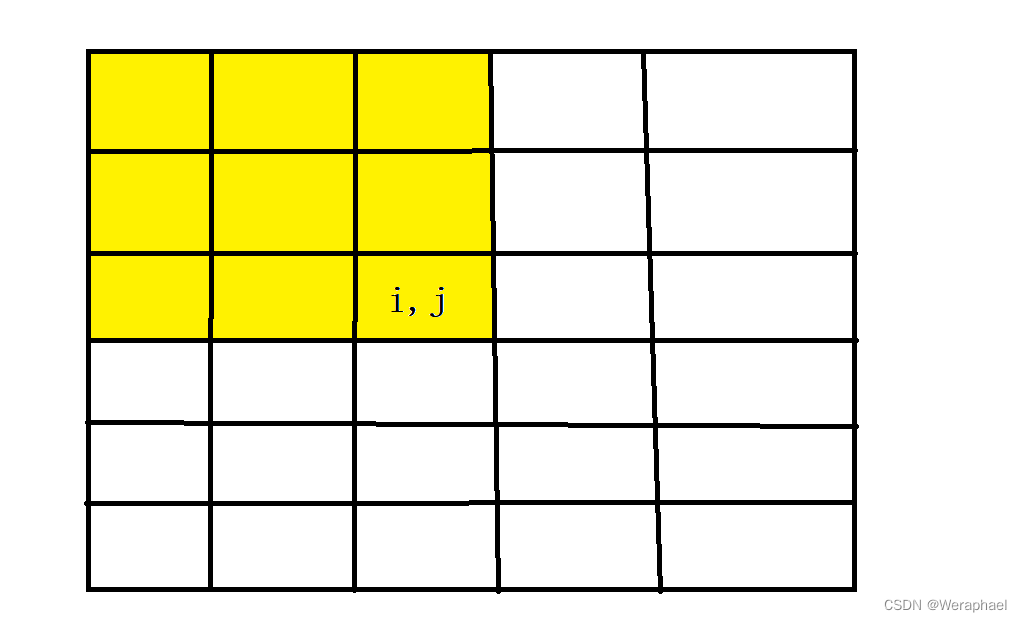
在这里插入图片描述

我们可以分三步求出黄色部分的和

第一步先求出红色部分所有数的和

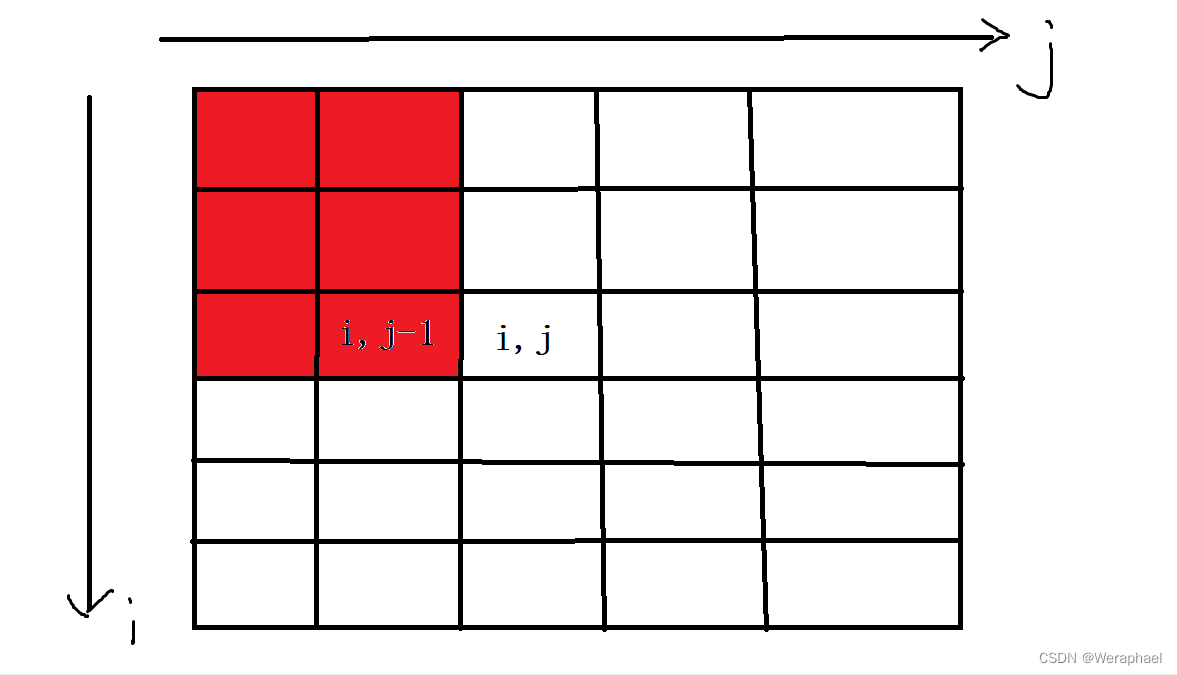
在这里插入图片描述

列出式子：S[i][j] = S[i][j-1] + ...

第二步再求出绿色部分所有数的和

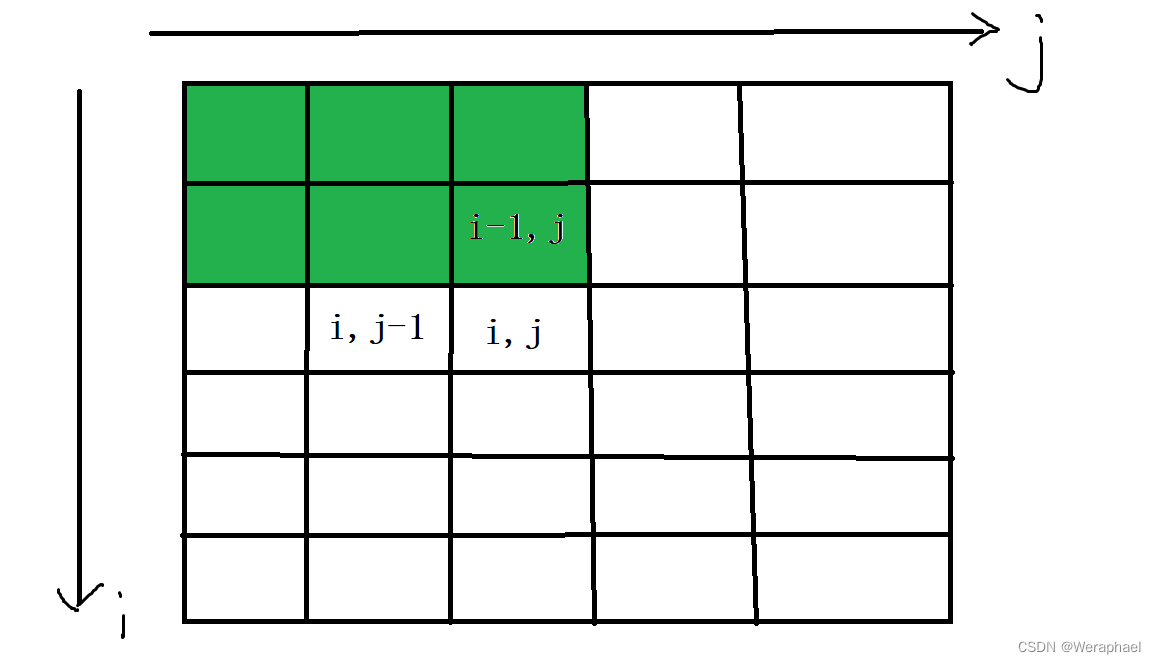
在这里插入图片描述

列出式子：S[i][j] = S[i][j-1] + S[i-1][j] + ...

第三步去重，因为前两部重复加上了黑色部分所有数的和，因此要减掉一次

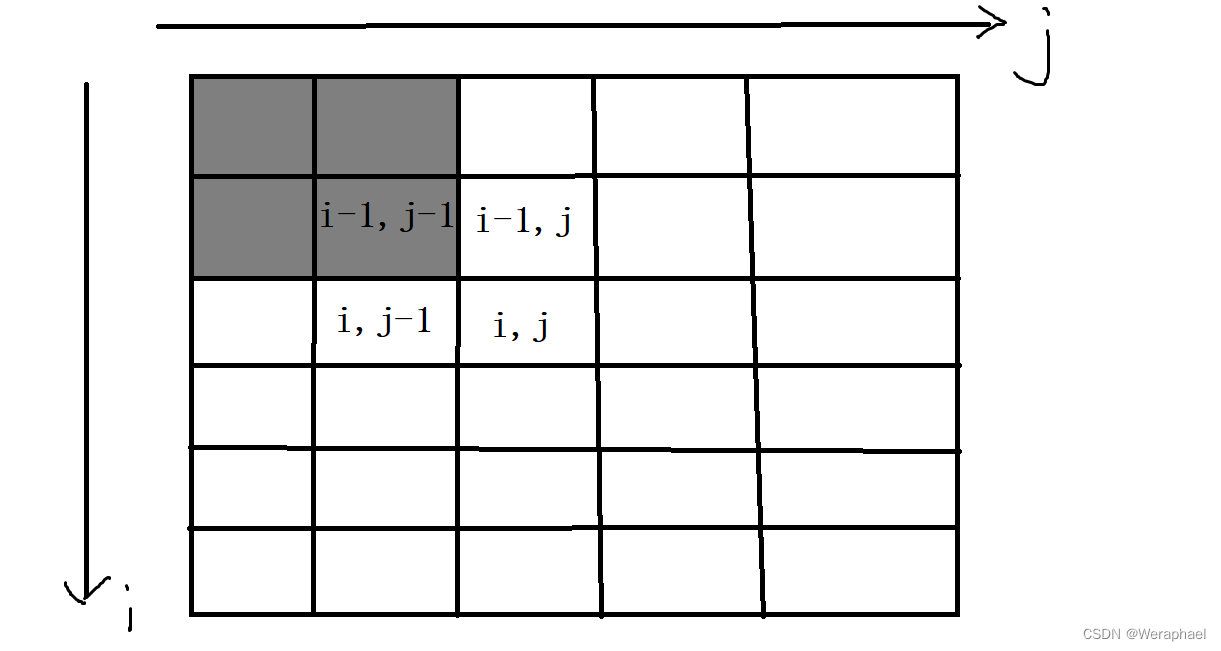
在这里插入图片描述

最后别忘了加上了本身：a[i][j]
列出式子：S[i][j] = S[i][j-1] + S[i-1][j] - S[i-1][j-1] + a[i][j]

2.3 子矩阵求法

假设要求左上角为（x1，y1），右下角为（x2，y2）所围成黄色部分所有数的和

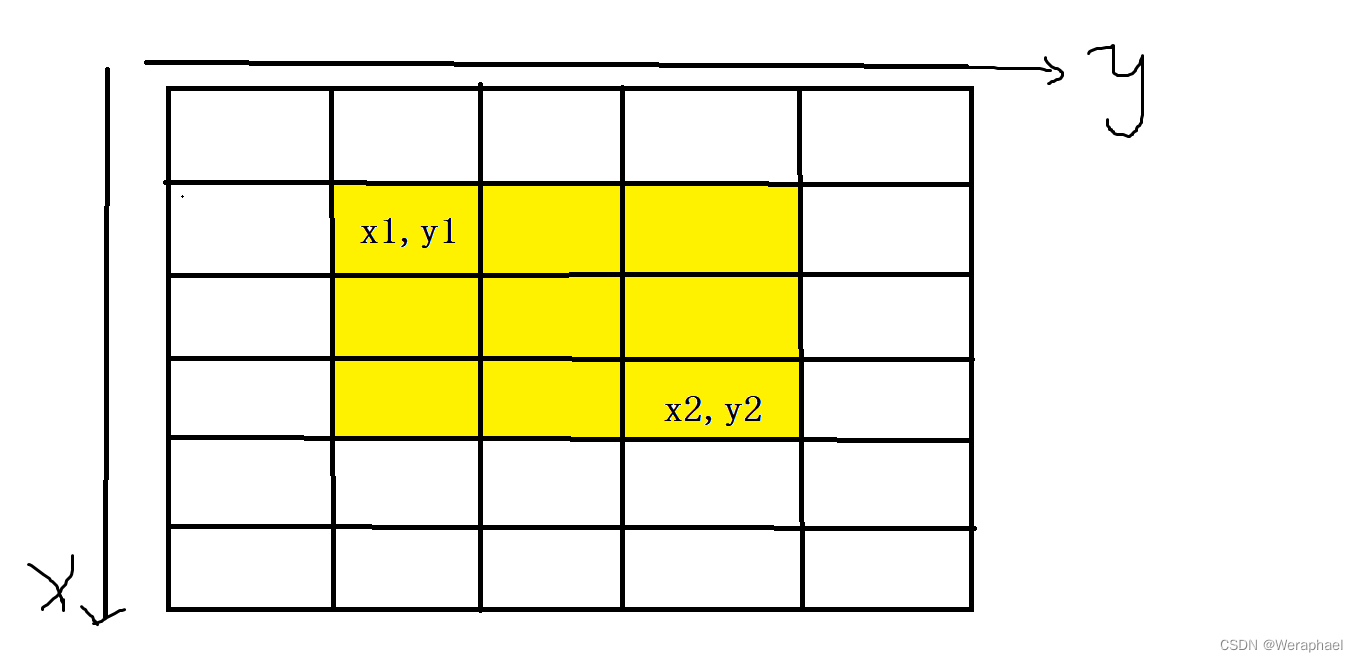
在这里插入图片描述

子矩阵的求法和求S[i][j]是类似的，四步走

第一步，先求出红色部分围成所有数的和

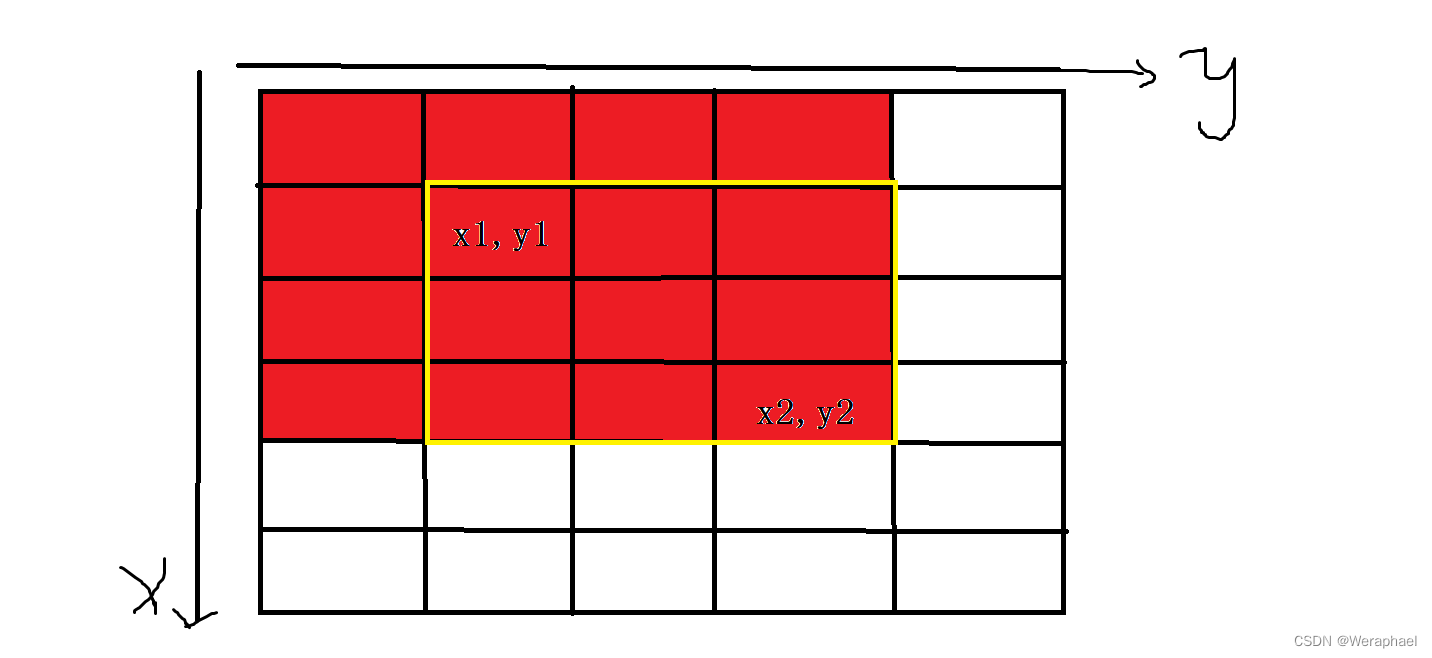
在这里插入图片描述

列出式子：S = S[x2][y2] - ...

第二步，在用上一步红色部分减去绿色部分所有数的和

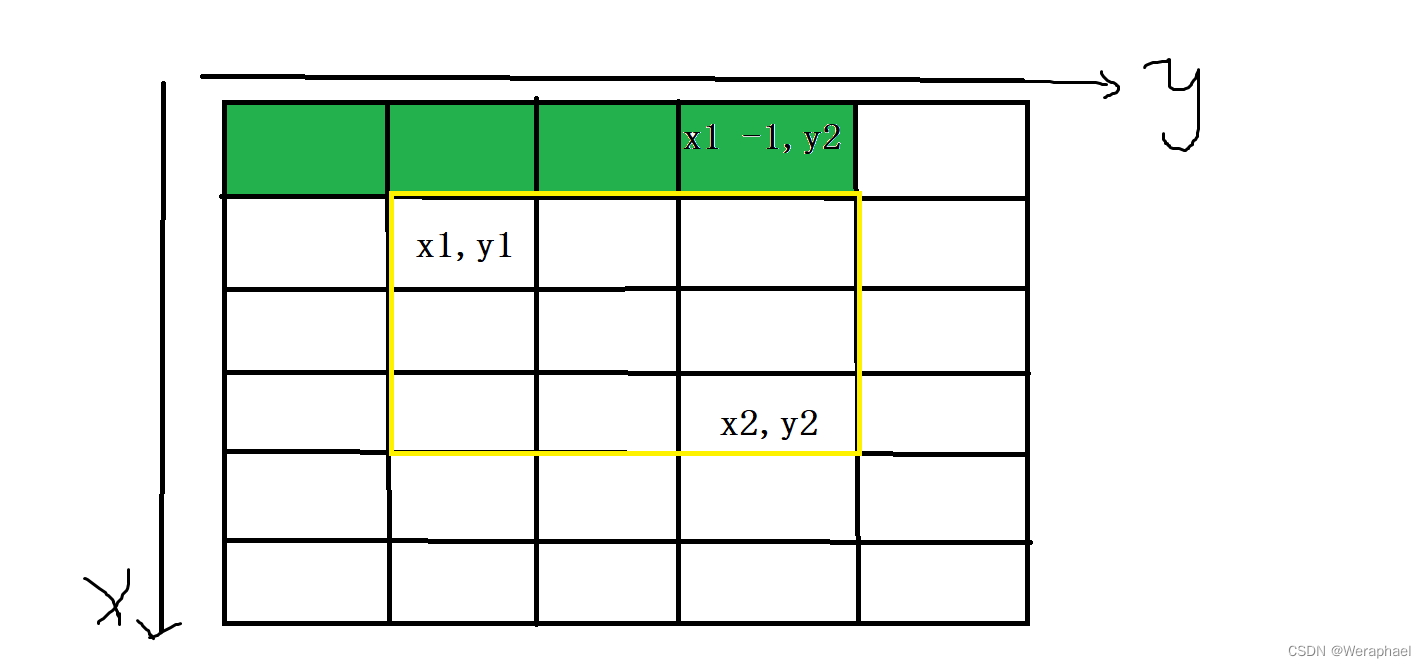
在这里插入图片描述

列出式子：S = S[x2][y2] - S[x1 - 1][y2] - ...

第三步，再减去灰色部分所有数的和

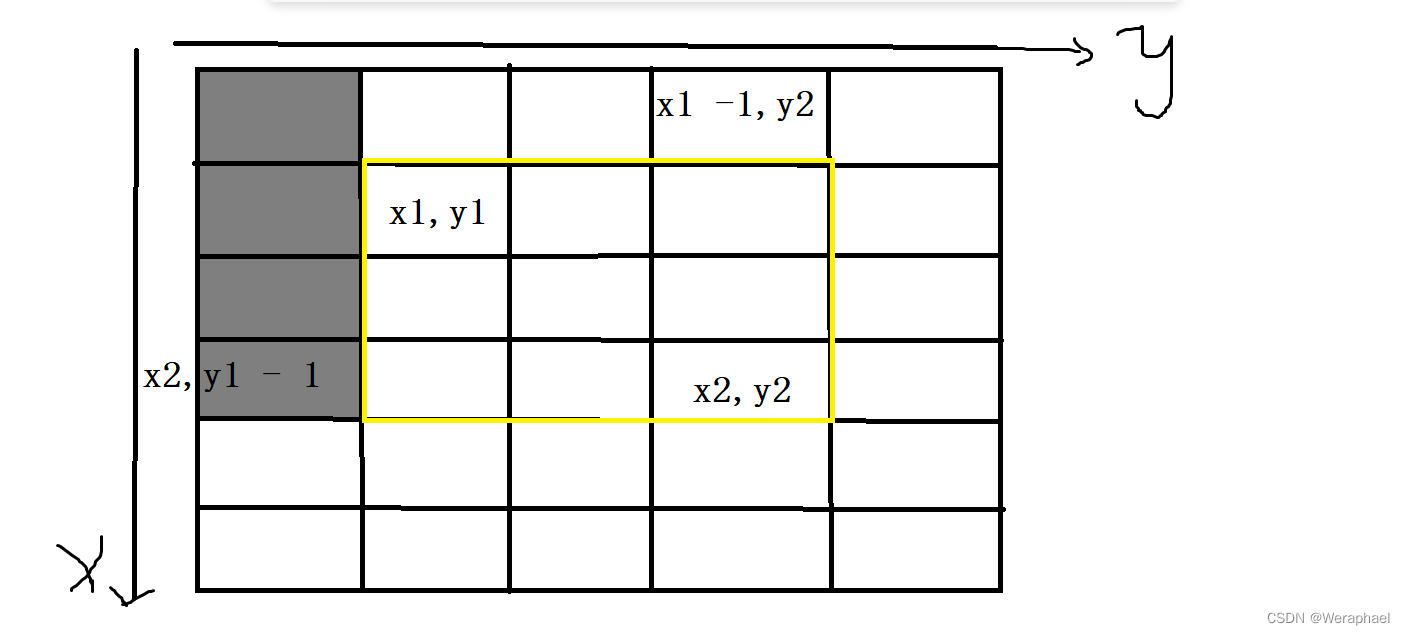
在这里插入图片描述

列出式子：S = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + ...

第四步去重，因为前两部重复减去了紫色部分所有数的和，因此要加上一次

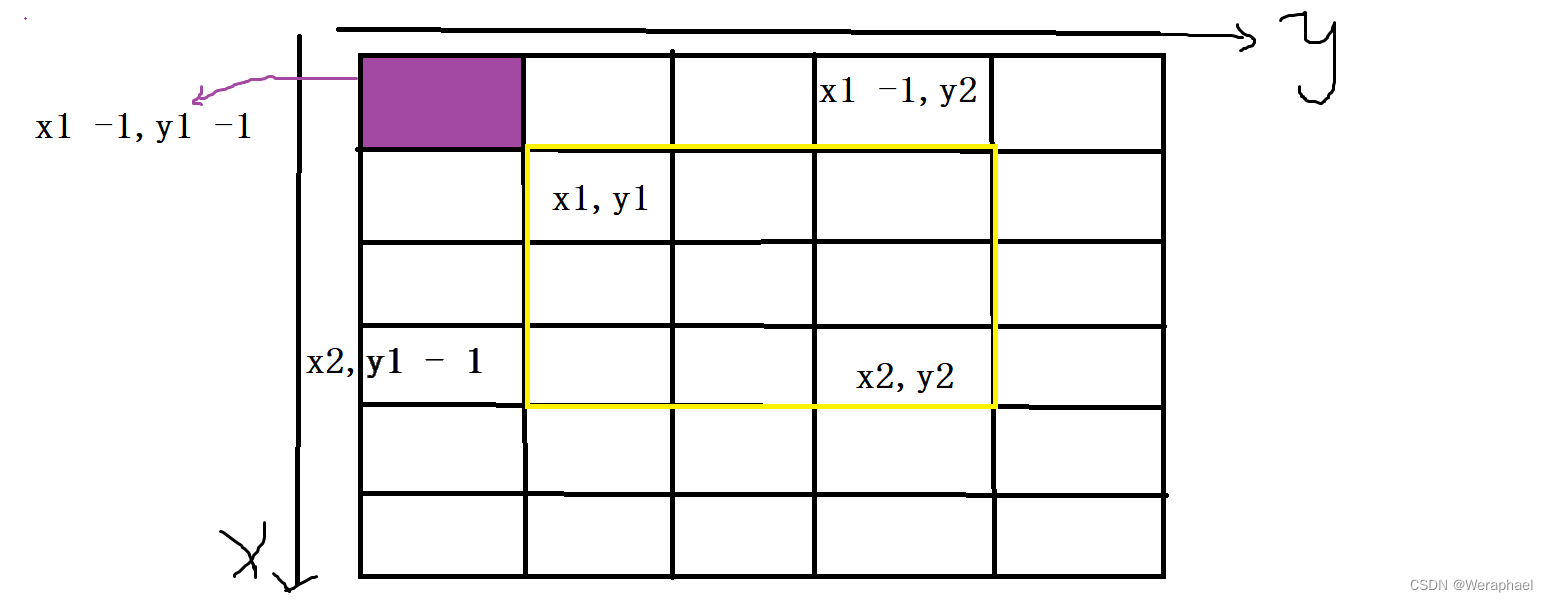
在这里插入图片描述

列出式子：S = S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]

2.4 代码模板

#include <iostream>
using namespace std;

const int N = 10010;
int n, m;
int a[N][N],s[N][N];

int main()
{
    scanf("%d%d%d", &n, &m); //n -行 m - 列

    //输入数组
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);
    
    //二维前缀和公式
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];

    //求子矩阵
    int x1, y1, x2, y2;
    scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
    printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);

    return 0;
}